The bullet hits a wall and stops. What stops it? The force which the
wall exerts on the bullet stops it. It begins expanding when it first
touches the wall; a point off axis will start moving perpendicular to
the direction of the bullet's velocity which has to mean that it is
feeling forces from other parts of the bullet since that point is not
touching the wall.
The bullet has
kinetic energy when it hits the wall. After it stops, that energy is
gone. Where did it go? Part of the energy went into doing the work
necessary to "squish" the bullet and part was lost to internal friction
intrinsic in squishing something soft but not elastic and ends up as
thermal energy�the squished bullet is hot.
 QUESTION:
QUESTION:
I am trying to help my son understand velocity, but find myself confused.
-
Person A drives in a circle. A physics website tells me this represents acceleration, a change in velocity, because his direction is constantly changing even though his speed may not be. Fair enough.
-
Person B takes a step forward and then a step backward to his original position. A different physics website tells me that this represents zero velocity, no acceleration, because he has not changed position.
But these answers seem contradictory, because person A, driving in a circle, will arrive at his original position at some point. In this respect, he is no different than person B, and could be considered zero velocity.
Can't both of these examples be considered changes in velocity? I suppose it depends on the timeframe you use to measure the change in position (?). So the person driving in a continuous circle can be considered to not be accelerating in some cases? This makes no sense.
 ANSWER:
ANSWER:
The first example refers to the instantaneous velocity
and the instantaneous acceleration of person A; instantaneous refers
to an instant in time and both acceleration and velocity are continuously
changing. The second example refers to average velocity and average acceleration. Average refers to the value of the quantity
averaged over some time period and the time period here is the time from
when he first stepped forward until he finished stepping back. Suppose that
was 10 s and the length of his step was 1 m; then the average velocity is
distance traveled divided by the time, 0/10=0 m/s and the average
acceleration was the change in velocity divided by the time, 0/10=0 m/s2.
Person A's average velocity and acceleration over exactly one time around
would also be zero.
 QUESTION:
QUESTION:
I'm having a really hard time understanding something my professor asked me to think about today in my entry level physics class. How can someone ever tell if they are moving if they have no clues of the outside. (sound or sight) If I had a penny and threw it up it would just fall back down, so that would not work. I'm really stumped here!
 ANSWER:
ANSWER:
This is the heart of a profound physical and philosophical
concept. The laws of physics determine the outcome of any experiment you
might perform; for example, Newton's three laws of classical mechanics and
Maxwell's equations describing electromagnetism are laws of physics. Suppose
you have performed experiments to discover these laws in some particular
frame of reference and you convince yourself that they are laws which apply
and are reproducible for any mechanical or electromagnetic experiment you
can think of. Now you decide to redo all your experiments but in a frame of
reference which moves with a constant velocity relative to the original
frame; you discover a really remarkable thing�the laws of physics are
identical in this new frame. You can then logically say that there is no
experiment you can perform to determine which of these frames is moving and
which is at rest. This is called the principle of relativity and frames in
which the laws of physics are true are called inertial frames of reference.
Any frame which moves with constant velocity relative to one inertial frame
is also an inertial frame. Essentially, there is no such thing as absolute
rest or absolute velocity. The laws of physics are not true in accelerating
(noninertial) frames.
Here is a little more information if you are interested: Newton's laws turn
out to be not true for velocities comparable to the speed of light; at high
speeds, however, the principle of relativity is still true provided that
Newton's laws are corrected (theory of special relativity). Also, it turns
out that the principle of relativity is true for all frames, not just
inertial frames, provided that you introduce a new principle, the
equivalence principle. The equivalence principle states that there is no
experiment you can perform which can distinguish whether you are in a
gravitational field with gravitational acceleration a or in a
noninertial frame of reference with an acceleration a. The
generalized principle of relativity and the equivalence principle form the
basis of the theory of general relativity which is the modern theory of
gravity.
 QUESTION:
QUESTION:
My question is this, If you are driving in a car (100km/h) and roll down
your window a vacuum is created in your car. but what if there is a 100km/h
tail wind. does the wind going the same direction cancel out the effect of
the vacuum?
 ANSWER:
ANSWER:
The reason air is drawn out through the open window is
Bernoulli's law, which states that when the velocity of a fluid increases
the pressure decreases. Therefore, the pressure outside the window (moving)
is lower than inside (not moving). This is easy to demonstrate by a smoker
inside the car and the smoke being drawn out the window. If there is a
tailwind with the same speed as the car, the air outside the car will not be
moving with respect to the car and there will therefore be no pressure
difference.
 QUESTION:
QUESTION:
If we see an atom and see all shells and subshells then will I find 3d First or 4s and if we see 4s first then why didn't we name it any other subshell of 3rd shell means why is it 4s? I know that it is chemistry related question but I m confused.
 ANSWER:
ANSWER:
The letters and numbers mean something. The letters tell you the
angular momentum quantum number of electrons in that shell. The letter s
tells you that l=0 and 4 tells you that it is the 4th l=0 shell, that there
are 1s, 2s, 3s shells with lower energies. The letter p means electrons have
l=1, d means l=2, f means l=3, etc. This peculiar labeling of angular
momentum quantum numbers is a historical artifact where the words sharp,
principal, diffuse, and fine were used to describe spectral lines.
 QUESTION:
QUESTION:
If two neutrons (just for the sake of ignoring charge) were separated from each other 1 light year, how long would it take for them to "touch" each other based on their gravitational attraction only? They are also in complete isolation from the rest of the universe.
 ANSWER:
ANSWER:
This is a very strange question. I have answered a nearly
identical question before but with much larger masses and smaller distances,
but the method is identical so I refer you
there. For your masses I calculate about 14x1018 years, about
a billion times the age of the universe. (I would also like to add that I do
not believe that this should be taken too seriously because no theory of
gravity has been accurately tested for either such large distances or such
small masses.)
 QUESTION:
QUESTION:
I am a fabricator and I currently have a task where I am attempting to create a braking system for downhill rapid propulsion (downhill racing).
Although the product exists, it is primitive and not fit for extreme measures, reliabilty, or convenience. There are many variables besides weight, drag coefficient, mass and gravitational acceleration. I would greatly appreciate your professional advice on creating a formula in which
I could create, change or gauge different systems for different masses. I have done much research and am increasingly frustrated yet interested.
I have come too some conclusions and have run many tests. I am using a polyester blend material for the canopy that is expansive and durable yet retractable, however. My cable system and my rapid cut down on drag are a problem. So my question is if
I weigh 160 pounds I am traveling at a speed between 30-60 miles per hour (we will say 45mph) at a down grade of 45% and i would like a slowing to 10 miles per hour between 40-50 feet from deployment. What would my initial area of my canopy be and what would the tensil strength of my cable need to be set at?
There are 3 points of contact for the cable system two high and one low.
 ANSWER:
ANSWER:
First, all air drag calculations are approximate and without
extremely complex computer simulations you can only do order-of-magnitude
calculations. Since you do not mention any sliding or rolling friction of
whatever is going down the incline, I will assume they are negligible. There
are, therefore, two forces on the mass, the gravitational force down the
incline mgsinθ and the drag of your "canopy" up the incline
which I will take as c2v2; here v
is the speed, m the mass, g the acceleration due to gravity,
θ the angle relative to the horizontal, and c2 is a
constant determined by the geometry of your canopy. A reasonable
approximation for c2 is c2≈�A
where A is the area presented to the direction of motion of the
canopy (only valid in SI units). Since I am a scientist, I will work
entirely in SI units here. Newton's second law, which governs the motion of
this system, is mdv/dt=-mgsinθ+�Av2
or dv/dt=gsinθ[1-(v2/vt2)]
where vt2=mgsinθ/c2=4mgsinθ/A;
vt is called the terminal velocity, the speed to which the
mass will slow as it goes forward. Solving the differential equation (this
is worked out in any intermediate-level classical mechanics book), the
following equation is found: v2=vt2(1-exp(-2gxsinθ/vt2)+v02exp(-2gxsinθ/vt2)
where x is the distance traveled and v0 was the
speed where x=0. That is everything you need since you know
everything except A. And you may want to use a fancier value for c2
more tailored to the details of your canopy. As an example, I will use
your numbers: m=160 lb=73 kg, v0=45 mph=20 m/s, v=10 mph=4.5 m/s,
x=45 ft=13.7 m, θ=450.
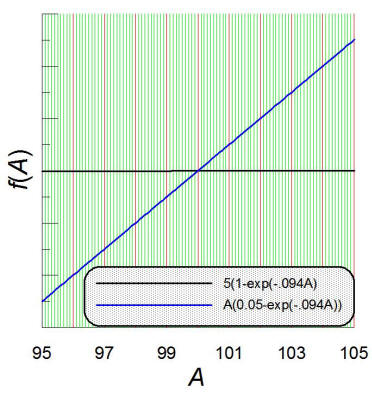
Putting these in, I find 20≈(2000/A)(1-exp(-0.094A))+400∙exp(-0.094A)
or A(0.05-exp(-0.094∙A))=5(1-exp(-0.094∙A)). Someone
more clever than I could probably solve this analytically for A, but
I will just solve it numerically by plotting the left and right sides of the
equation and finding the intersection (see inset figure on the left). I find
that A≈100 m2≈1000 ft2; this would be a square
about 30 ft on a side. (Since A is so large, one could have easily
solved this by simply neglecting the exponential functions, 0.05A≈5.)
Regarding the strength of the cables, since I do not have any details about
the design of the canopy, the best I can do is tell you the maximum force
the canopy would exert on the mass via the three cables. Since the
acceleration is -gsinθ+�Av2/m, the
greatest acceleration is when the velocity is greatest, when the braking
initiates. So, the force the cables must exert is -mgsinθ+�Av02
or -mgsinθ+c2v2. For
your specific example, this force would be about 9500 N≈2100 lb or roughly
700 lb/cable.
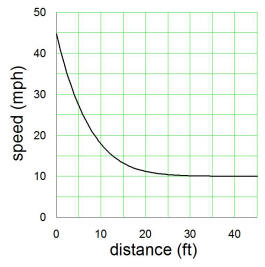
The figure on the right shows the solution I have come up with. Indeed it
begins at 45 mph and drops to 10 mph at 45 ft. However, one might just as well
say that the speed is also just about 10 mph at 25 ft, just not exactly.
That is the problem with analytical solutions sometimes�they demand
exactness. To me this graph says that you could get away with a
significantly smaller canopy and still qualitatively achieve your goal. I
think I have done enough here setting stuff up and you could proceed and
investigate how much things would change if you changed your speed at 45 ft
to be 11 mph, e.g. And, don't forget, these are approximate solutions
to be used as a rough guide.
 QUESTION:
QUESTION:
Say I am a stationary observer and observe a rocket launched from earth to Proxima Centauri which is about 4.35 light years away from us the rocket has a constant acceleration of 1g or 9.8m/s2 for half the trip and -1g for the other half. Newtonian kinematics states xf=xi+vt+at2/2 yet over the course of time my velocity will become relativistic and the equation no longer applies.
What is the correction needed for me, a stationary observer, to solve how long it will take the rocket to reach its
destination?
 ANSWER:
ANSWER:
It turns out that I have already solved
this problem;
I have found a solution for the distance as a function of time for a
constant force F rather than the time as a function of distance, but
that can easily be inverted. I showed that x=(mc2/F)(√[1+(Ft/(mc))2]-1);
in your case, F=mg, so x=(c2/g)(√[1+(gt/(c))2]-1).
Solving for t, t=√[(x/c)2+(2x/g)].
For the first half of the trip, x=2.175 ly and I calculated that g=9.8
m/s2=0.11 ly/yr2, so t=6.58 yr. Given the
symmetry of the situation, the total time for the trip, as observed by you,
is 13.2 yr. Using the result from the
earlier answer,
v=(gt)/√[1+(gt/c)2],
I find that the speed at the midpoint of the trip is 0.89c. The
average speed for the whole trip was 4.35 ly/13.2 yr=0.33c.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
What is the correction to determine how much time the rocket will have
perceived to have passed?
 ANSWER:
ANSWER:
The mathematics gets a little difficult here but it is a common
problem which has been worked out. I will just give you the final result.
For more detail, see the blog by John Baez on the
relativistic rocket. For a rocket with acceleration
g halfway to
a distance D in light years and then with deceleration g the rest of the way, the
elapsed time T in years on the rocket is T=1.94∙arccosh[(D/1.94)+1)].
So, for D=4.35 ly, T=3.58 yr.
 QUESTION:
QUESTION:
I'm a climber and I constructed myself an anchor that I fixed to a rock wall. To test it, I hooked to it a 12mm in section steel cable with a length of 2,8m and a concrete block of 30kg to the other tip. I then dropped it from anchor level and it held. I am now wondering what kind of impact force was developed in this test.
 ANSWER:
ANSWER:
There is no way to know this because what matters is how long it
took the block to stop after the cable was straight. One could easily
estimate how long it took to fall to the stopping point, about T≈√(2.8x2/9.8)=0.76
s. The speed then would be v≈9.8x0.76=7.4 m/s. The average force would be
F≈9.8x30+30x7.4/t=294+222/t where t is the time to to stop.
For example, if it took a tenth of a second to stop, the average force felt
by the block and therefore by the anchor would be 2494 N≈561 lb. For more
detail, see the faq page.
 QUESTION:
QUESTION:
If you travel a set speed standing in the back of a truck (ex 60mph) and you throw a ball forward at 60mph, does that ball at any point in time double it's speed to 120mph.
 ANSWER:
ANSWER:
This seems one of the most misunderstood things in physics.
Speed has no meaning unless you state what the speed is relative to. In your
example, the speed of the baseball relative to you is 60 mph and the
speed relative to the road is 120 mph. If there is another truck
coming toward your truck with a speed of 60 mph, that truck sees a speed of
the baseball of 180 mph. If there is another truck passing you and going 120
mph, he sees the ball with zero speed. The bottom line is that there is no
such thing as "absolute speed", it all depends on who measures it. And
certainly the ball does not double its own speed.
 QUESTION:
QUESTION:
Physics says that energy is always conserved in any form. My question is what happens to the energy contained in me if I die? In what form is it transformed?
 ANSWER:
ANSWER:
Actually, "physics says" that the energy of an isolated system
(no external forces doing work on it) is conserved. Or, you could say that
the energy of the entire universe is a constant. So, let's talk about what
energy there is in your body. Mostly, it is simply the mass of all the atoms
in your body, E=mc2 and this does not change because as
your body decays, all the atoms are indestructible. However, much of the
molecular structure of your body changes. I do not know that much detail
about microbes and organisms which hasten decay, but essentially they will
extract energy from fats and sugars and use it for their own purposes. I
assume that heat will also be a result of decay.
 QUESTION:
QUESTION:
i was wondering if you could tell me why we measure the angles from the normal and not the reflective surface and also could you explain the difference between regular and diffuse reflection.
 ANSWER:
ANSWER:
No really important reason that I can think of, it is just
convention. There are situations in physics where a surface is conveniently
denoted as a vector and that direction is normal to the surface, not
parallel. Diffuse reflection refers to reflection from a surface which is
rough rather than smooth. A nice little app letting you see this kind of
reflection may be seen
here.

 QUESTION:
QUESTION:
I was recently at the Map and Government Library of the main library and stumbled upon a stereoscope map reader. When held over two accurately aligned aerial photographs of the hills and valleys of Gordon, Georgia, I can see one image of the trees and hills "popping up" as if they are 3-D. Both lenses are concave, and I was wondering how does the picture appear 3-D?
 ANSWER:
ANSWER:
First, we need a tutorial on how we see the world in 3-D.
Because we have two eyes (binocular vision), each eye sees a slightly
different image of the world because of
parallax. One of the
first things the brain of a newborn baby learns is how to interpret these
two images as a 3-D picture. If you had two cameras separated by the
distance between your eyes, the pictures would be slightly different. A
simple photograph, of course, contains only information from one perspective
and therefore lacks the 3-D quality. In the 19th century cameras
were designed with two lenses to form two images. If you then viewed one
image with one of your eyes and the other image with your other eye, you
could see the photograph as you would if you were looking at the original
object, i.e. in 3-D. The viewer is called a
stereoscope. The
purpose of the lenses is to allow you to view the very close photos with a
relaxed eyes.
 QUESTION:
QUESTION:
We can use the work-energy theorem in any inertial frame of reference.
When no external force is applied, and there is no change of height, the change in KE = -(Change in PE(spr)).
However, KE change depends upon the frame of reference and the extension of a spring does not depend upon frame's choice! HOW IS THIS POSSIBLE?
 ANSWER:
ANSWER:
The extension of the spring is the same in both frames, but the
work done by the spring is not because the same force acts over a different
distance in the moving frame. Forget potential energy and simply write ΔK=W
where W is the work done by any conservative external force, W=0∫XF(x)dx.
I have chosen the starting position as x=0; to keep the algebra
simple, I will also choose the starting velocity in this (x) frame to
be 0 and the final velocity to be V, so ΔK=�MV2=W.
Suppose that it takes time t to reach the position X. Now,
suppose there is another reference frame (x') which has a speed U
in the +x direction and x'=0 at t=0 also. Then x'=x-Ut and the initial velocity is
U and the final velocity is
U-V in this frame, so ΔK'=�M(V-U)2-�MU2=�MV2-MUV.
Finally, calculate the work done in the moving frame: W'=0∫X'F(x')dx'=0∫X-UtF(x-Ut)(dx-Udt)=W=0∫XF(x)dx-U0∫tF(t)dt.
The second integral is the impulse which is the change in momentum,
MV, so W'=0∫XF(x)dx-MUV=W-MUV.
Putting it all together, ΔK'=W'=�MV2-MUV=W-MUV
or �MV2=W.
 QUESTION:
QUESTION:
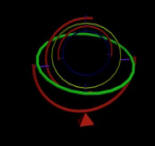
In the figure to the right, green ring is rotated about horizontal axis, yellow ring is made to rotate about vertical axis and innermost blue ring is made to rotate about horizontal axis and
I want to make this system self sustained with the help of induced current and magnetic induction.
I am facing difficulty in finding angular momentum.
What will be the angular momentum if a ring is made to rotate about the horizontal axis passing through its centre?
 ANSWER:
ANSWER:
The moment of inertia I of a thin ring of radius R
and mass M about a diameter is I=�MR2. Angular momentum is
Iω where ω is angular velocity in radians/second. Good luck
making this "self sustained"!

 QUESTION:
QUESTION:
I have a remarkable image relating to the speed of light. It begins "and
God said," and then contains some 30 or 40 detailed equations, then finishes
with "and there was light." This is NOT the well known set of 4 Maxwell
Equations which has been made into a tee shirt (I wear one proudly!), but a
much more sophisticated treatment of the same subject. I am looking for a
detailed interpretation of the 30 or so equations, several of which I recognize, but many of which I do not. Can you help or suggest where we might such a treatment? I believe you can find the image I am referring to fairly easily by Googling for light equations or something similar.
 ANSWER:
ANSWER:
The original �and God said� T-shirt is infinitely more
elegant than this one. This one is trying to be so cool that it comes off as
pretentious! Here are some of the things in this mess of stuff which are
extraneous to light: expressions for Bessel functions, one-dimensional
Schr�dinger equation, three-dimensional Schr�dinger equation, Coulomb's law
(already in Maxwell's equations), LaPlace's equation in spherical-polar
coordinates, dependence of mass on velocity (special relativity and
irrelevant for massless photons), other stuff from special relativity
(already contained in Maxwell's equations), one-dimensional harmonic
oscillator energy, deBroglie's hypothesis, etc. The only thing
Maxwell's equations do not include that God certainly needed to add was the
concept of a photon, E=hf=pc. God would have made his prouncements as
concise as possible; see
Occam's Razor.
 QUESTION:
QUESTION:
I am lying on the surface of the earth. I don't have Kinetic energy because I am not in motion. I also cannot have any potential energy because my height raised from the surface of the earth is zero. Does it means I don't have any energy in me?
 ANSWER:
ANSWER:
But, you have potential energy relative to the bottom of a
nearby hole, don't you? And if someone on the moon observed you he would say
you were moving, so you would have kinetic energy as seen by him, wouldn't
you? Energy is not absolute but "in the eye of the beholder". Also, we know
that there is lots of chemical potential energy stored in the fat of your
body. Also, we know that there is energy simply because mass is a form of
energy, E=mc2.
 QUESTION:
QUESTION:
Suppose i am inside a uniformly moving spaceship and I send a light beam perpendicular to the direction towards the opposite wall. since the spaceship is moving and according to relativity light doesn't feel any sort of "kick", shouldn't the light beam be off the target and thereby letting me know that
I am moving?
 ANSWER:
ANSWER:
If you aim at a spot on the wall you will hit it. You will observe the light beam going straight across the ship.
The reason is the principle of relativity which states that there is no
experiment that you can perform which can distinguish whether you are at
rest or moving with constant velocity. You could also fire a rifle at the
opposite wall and hit the target. An observer outside your spaceship,
however, will see the light with a component of its speed in the direction
you are moving but will still see the speed of the light as being c and the light hit the target. Your experiment would be different, however,
if you were accelerating forward; the light would miss the target for the
same reason that if you were to aim a rifle directly at a target on earth it
would fall some on the way there. You might be interested in the
light clock. Your space ship could be thought of as a light clock which
ticks once when the light hits the target.
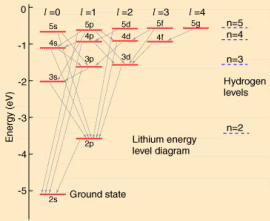
 QUESTION:
QUESTION:
We did a lab where we put lithium in a flame and saw it emitted red light.
We were told this happens because an electron gets so much energy it jumps from one electron shell to the next. Then when it falls back to the lower energy level, it gives off photons of light.
We are having trouble understanding what is happening to the electrons. Lithium has two electrons in the first energy level and one in the second. Does an electron in the first shell jump to the second? Or does an electron in the second jump out to the third?
And if it is an element with 3 orbitals, does an electron jump from the first to the second, and if it does, does an electron also move from the second to the third?
How does the movement of electrons from one shell to the next affect the other electrons in that shell?
 ANSWER:
ANSWER:
The figure to the left shows the energy-level diagram of
lithium. The thing to understand is that the two inner electrons (in the 1s
shell) are essentially inert for your experiment, only the outer electron
gets excited. So the outer electron (in the 2s shell) looks in and sees the
nucleus, charge +3, shielded by two electrons, charge -2, for a net charge
of +1. In other words, the lithium spectrum should look a lot like the
hydrogen spectrum because the active part of the lithium atom looks pretty
much like a hydrogen atom. Note, for comparison, the energy levels for
hydrogen shown on the figure. The red line, with a wavelength of about 670
nm, results from the transition from the first excited state (2p) to the
ground state (2s).
 QUESTION:
QUESTION:
When Cavendish calculated the value of universal
gravitational constant he used mass of lead balls as reference. But how did
he know mass of the lead ball if he doest know the value of G?
 ANSWER:
ANSWER:
He could simply weigh them because we know W=mg. Since
you can also write W=mMearthG/Rearth2,
you can identify g=MearthG/Rearth2,
and g is easy to measure even if G is not.
 FOLLWOUP QUESTION:
FOLLWOUP QUESTION:
How did he build a weighing scale.
When weight is determined using a scale it should have been built w.r.t certain standard mass. But with out knowing value of G there is no way
 they had a standard mass. He could have weighed a 10kg mass as 1kg mass. So, how did he weight exact mass.
they had a standard mass. He could have weighed a 10kg mass as 1kg mass. So, how did he weight exact mass.
 ANSWER:
ANSWER:
The kilogram was officially defined in 1795 as the mass of 1
liter of water. The Cavendish experiment was performed in 1797-98. Even if
the kilogram were not defined, there were other mass definitions which
Cavendish could have used. As an example, let me consider the oldest
standard weight I could find reference to, the beqa (b) (shown in the figure) defined
about 5000 years ago as the mass of 200 grains of barley corn which is about
6.1 grams=6.1x10-3 kg. So if Cavendish had used the b as his mass
standard, he would have found G=6.67x10-11 kg2/(N∙m2)=6.67x10-11
[kg∙s2/m3]x[1 b/6.1x10-3 kg)=4.07x10-13
b∙s2/m3] (assuming that he used seconds and meters for
time and length). It is a different number but means exactly the same thing.
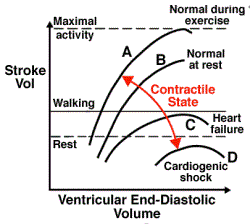
 QUESTION:
QUESTION:
I have a strange request.
I'm a nurse practitioner, I learn, like most people by seeing a picture or being shown the way something works. I don't know if you've heard of Frank-Starling curve related to the heart, it's the idea of volume or pressure on horizontal line and stroke volume or cardiac output
(CO) on vertical. The idea is more vol will help, too much will over distend and be less stroke volume or CO.
I have the idea of the spring with the weights on it to show this. But I really need something to exhibit this example.
 ANSWER:
ANSWER:
I hope I am not totally out of my depth here! I will attempt to
bring simple physics principles to bear on this question. I had never heard
of the Frank-Starling curve and did a little research to educate myself. The
curve basically shows, under various conditions, the relationship between
how much blood is loaded into the ventricle and how much of that blood is
then pumped out. Usually the absissa (x-axis, independent variable)
is something called
preload, but
the basics can be qualitatively understood by plotting volume of blood
filling the ventricle. In the figure to the left, focus on the curve labeled
B, Normal at rest. I interpret this as the result of the heart acting
as an elastic membrane and stretching as blood is added. As the membrane
stretches it behaves like a two-dimensional spring and the basic property of
a spring is approximated by Hooke's law which essentially says that the
force exerted by the spring is proportional to how much it is stretched.
Hence, adding more blood stretches the spring more and the more it stretches
the harder it pushes on the blood; therefore in a given time more blood will
be pumped out because of this greater force (pressure). This explains the
rise of these curves. Therefore, your idea of springs and weights is a good
one because elasticity is the key here, I think. Maybe even better would be
to take a couple of identical balloons and fill one with twice the air as
the other; then letting the air flow out for the same times, the fuller one
should blow out more air. Also, in times of stress or exercise, I have
learned that neurotransmitters are transmitted to the muscle cells in the
heart wall which results, via calcium ions, in stiffening the walls more so
that they exert even greater force (pressure) on the blood resulting in a
curve more like A, Normal during exercise. To demonstrate that, use
two different springs with different stiffness or use two different
balloons, one much harder to blow up than the other. Drugs can also be used
to try to adjust the shape of the curve, e.g. digoxin or calcium
channel blockers. Note that in curves C and D a point of diminishing returns
is reached actually causing the output to begin dropping with increased
input. I guess this could be likened to reaching an elastic limit like when
you stretch a spring too far and it will not go back to its unstretched
length.
 QUESTION:
QUESTION:
I've been wondering about the hazards of traveling at high speeds in
space for a while and the challenges it would bring for us in terms of
spaceship design. My main interest is interstellar travel and how meteors
might affect the safety of such an exercise. So if we had a spaceship that
would accelerate to let's say 7 percent c and we sent it along with some
colonists to Alpha Centauri and the ship while traveling 7 percent c hit a
meteor the size of a man's fist, how catastrophic would an impact of this
nature be to the spaceship?Let's say the meteor was 10cm across and was
comprised of iron.
 ANSWER:
ANSWER:
There is no way I can even begin to do a calculation here. It
would depend on the design of the space ship. Even if I had more details,
this would be more of an engineering problem than physics. You can use your
imagination, though. The shuttle Columbia was going 545 mph=11 m/s≈0.000004%
of c and a piece of foam insulation (much softer than iron) had
catastrophic results. You might be interested in another
recent answer.
 ADDED ANSWER:
ADDED ANSWER:
I estimate your meteor would have a kinetic energy of about 2x1017
J, about the same as 2,000 Nagasaki atomic bombs. Curtains for this space
ship!
 QUESTION:
QUESTION:
On a Disk or a Sphere. What is the Centrifugal force on matter when the Disk/Sphere is spinning at half the speed of light?
 ANSWER:
ANSWER:
I presume you mean the circumference has v=c/2. This is
quite well approximated nonrelativistically (γ=0.97), so F≈mv2/R=mc2/(4R)
 QUESTION:
QUESTION:
I understand you don't answer questions about stars, but im wondering about the nuclear dynamics involved in nuclear fission. In a star with 250 solar masses or more there is something called photofission, where high energy gamma rays cause elements as light as tin to go through nuclear fission. I was wondering, how much energy would be required to cause fission to occur in the element tin?
 ANSWER:
ANSWER:
Right, this is certainly more nuclear physics than astrophysics,
so I can do some rough estimates for you. I can tell you approximately how
much energy is released in the symmetric fission Sn112
�>2Mn56. The binding energies of the tin and manganese are 953.5
MeV and 489.3 MeV respectively. So the energy released in the fission would
be 2x489.3-953.5=25.1 MeV. What I cannot tell you is what energy photon
would be required to cause the fission. This depends on the structure of the
Sn112
and how it interacts with the photon. Fission might be induced by a much
lower energy photon than 25 MeV. After all, uranium can fission with no
energy whatever added to it (spontaneous
fission).
 QUESTION:
QUESTION:
What is the Cosmological Constant and why it couldn't be described perfectly by Einstein?
Was only because of it that Einstein thought the universe was static?
 ANSWER:
ANSWER:
When Einstein proposed the theory of general relativity, around
1918, it was generally believed that the universe was static. General
relativity is the theory of gravity, and if gravity is the main interaction
among stars and galaxies, this is not possible; with only gravity, the
universe would have to be either expanding and slowing down or compressing
and speeding up. Therefore Einstein had to introduce something to balance
the universal gravitational force; this something was called the
cosmological constant. It was later discovered that the universe is
expanding and he later denounced the cosmological constant as "�my greatest
blunder�" Interestingly, several years ago it was discovered that the
expansion of the universe is actually speeding up implying some kind of
repulsive force, akin to the cosmological constant, often referred to as
dark energy; this has reignited interest in Einstein' "greatest (or maybe
not) blunder". I do not know what you mean by "�couldn't be described
perfectly�"
 QUESTION:
QUESTION:
What is the difference between atomic physics , nuclear physics , particle physics and high energy physics ?
 ANSWER:
ANSWER:
Atomic physics studies the atom, mainly the configurations and
properties of the electrons which characterize atomic structure; usually
atomic physics also includes molecular physics and chemistry may be thought
of as applied atomic and molecular physics. Nuclear physics studies the
properties of the atomic nucleus. Particle physics studies elementary
particles, constituents of atoms and nuclei. High-energy physics usually
refers to physics done using high energy particle accelerators, in the GeV
range or above, to study mainly nuclear physics or particle physics; can
also refer to cosmic ray physics. There is no clear boundary among these
areas of physics and there is often considerable overlap.
 QUESTION:
QUESTION:
If 2 people are standing in opposite directions but equal distance away from a firework why will one person hear it before the other? I have a very inquisitive child who heard something about this on a TV programme but can't quite remember exactly why and I don't know so please help me!!
 ANSWER:
ANSWER:
The only thing I can think of is wind. Sound moves with a speed
of about 840 mph relative to the air. For example, if there is a wind
with speed 30 mph blowing north relative to the ground, then the speed
of sound relative to the ground is 870 mph north and 810 mph south.
In that case, someone north of the firework would hear it sooner than
someone south.
.jpg)
 QUESTION:
QUESTION:
I was wondering if you could help me explain something that happen
whilst heating water using a bunsen burner the other day. I stopped heating
(turned the bunsen burner off) at 80 degrees, but the temperature of the
water (as read from a thermometer) continued to increase. This only lasted
for several minutes, but this is not what I had expected. Given that the
heat source was removed, I expected particles to begin to decrease in
kinetic energy, and therefore temperature decrease too. Am I correct in
thinking particles within water built up momentum during heating, meaning
they were still increasing kinetic energy and therefore temperature for a
short while after turning the bunsen burner off? This meaning the
thermometer increased in temperature too even though bunsen burner was off?
 ANSWER:
ANSWER:
Your speculation that the kinetic energies of the molecules
continued to increase because they were already increasing is wrong�energy
change does not have "inertia". The
instant you stop adding energy (heating) the water, its temperature will
stop increasing. Therefore, something must have continued heating the water.
If you think about it, the bunsen burner, while the ultimate source of the
energy, is not what is heating the water; the bunsen burner is heating the
container and the container is heating the water. The container is much
hotter than the water when the bunsen burner is turned off and it will continue
heating the water until the two are in thermal equilibrium, at the same
temperature (ignoring the interaction with the air around them).
 QUESTION:
QUESTION:
I want to know that as the height increses acceleration due to gravity decreases at diffent height so escape velocity should be different at every value h so will the acceleration due to gravity at height h will be rate of change of escape velocity with respect to time. If no then why beacause acc is the rate of change of velocity with respect to time?
 ANSWER:
ANSWER:
The escape velocity is defined as the velocity that an object at
rest at a particular point in a gravitational field must be given such that
it will be at rest when it has gone infinitely far from the source of the
field. So, you are right that the escape velocity from earth depends on the
altitude at which the object begins. So, it doesn't mean anything to ask
what the escape velocity is as a function of time, only what it is as a
function of altitude.
 QUESTION:
QUESTION:
I want to know how to caculate the distance a let say bike would fly if it
was projected off a ramp so that I would be able to predict where it will
land I have seen the equation but I don't understand it: R=vo2(sin2θ)/g.
 ANSWER:
ANSWER:
The equation you found is valid only if the bike comes down at
the exact same level that it left the ramp. I refer you to an
earlier answer for a more
general equation and the explanation. The earlier answer is in English
units. If you want to work in SI units, distances should be in meters (m)
and speeds should be in m/s, and g=9.8 m/s2.
 QUESTION:
QUESTION:
If a 55,000 pound vehicle slams into a stationary 2,200 pound vehicle at 25 mph, what amount of force is created at impact to occupant of smaller vehicle?
 ANSWER:
ANSWER:
There is no way to calculate this with this information. Let me
do a few calculations to show you what the problems are. If the two vehicles
stick together, you can use momentum conservation to get the speed v
of the two after the collision: 55,000x25=57,200v, so v=24
mph. I would prefer to do the calculations in SI units, so v=24
mph=10.7 m/s, m=2200 lb=998 kg. The momentum of the car after the
collision is p=mv=2.2x106 kg∙m/s. Now, we come to the crux
of this calculation (this is from Newton's second law, if you care): the
average force which caused the momentum to change is F=p/t=2.2x106/t,
where t is the time which the collision lasted and I do not know t.
For example, suppose the collision lasted � s; then the force was F=4.4x106
N=9.89x105 lb. That is the force the car feels. The occupant will
feel a much smaller force. Suppose, for example, that the mass of the
occupant is 200 lb=90.7 kg; then the momentum acquired during the collision
is 90.7x10.7=970 kg∙m/s. So, if it took � s for the occupant to acquire this
momentum, the force would be F=1940 N=436 lb. All these calculations
would be different if the two vehicles did not move off together after the
collision; the car and occupant would be moving faster than 24 mph so the
forces would be greater. And, without knowing how long the collision lasted,
you cannot know the average force applied.
 QUESTION:
QUESTION:
I was watching a documentary about quantum mechanics, and after about 4 min of the particle-wave duality I stopped to Google some questions, the 1st
I found right away, ie "what would happen if you fired a SINGLE electron. And at least from what i read, the result is still the refraction pattern. So then i got to thinking and this is where my question comes into play. From what i gather observing an object at the quantum scale affects the result, considering our eyes use photons that makes sense but my question is this... if we assume that at the very basic level, both photons and electrons are waves the entire time, could what we see as an observation of the electron be nothing more then an interference pattern created when the wave from the photons leaving our eyes interfere with the waves from the electron, and the point where that interference peaks, is what we "observe" as a particle? And by extension, could all known "particles" simply be varying degrees of interference caused by this effect? Furthermore, if we continue to assume that all particles are in fact waves from the beginning then could the interference of 2 non photons create interference that we observe as other "particles" when our photons interact with the interference pattern caused by those waves?
 ANSWER:
ANSWER:
It is hard to understand what your question is. But, you state that a single electron will give you a diffraction pattern. If this is what you literally mean, then that is wrong. A single electron will give you a single spot on the screen. The wave-particle duality example here is that if you shoot many electrons but one at a time, you will see the diffraction pattern emerge
(see the animation here). With regard to your speculation that "...both photons and electrons are waves the entire time...", this is exactly what wave-particle duality is not. Both are both all the time and you will observe the one which you look for in your experiment.
There is also a wonderful
video animation
(it's in the Brief History� section,
Animation showing the wave-particle dualitywhich illustrates the double slit for particles, waves,
particle-waves, and particle-waves where an observer determines the slit
through which slit the particle went through.
 QUESTION:
QUESTION:
Yesterday, In my exam, I was asked a short question. It was:
Does energy of light transfer while changing the medium as velocity differs? Give reason.
What might be the correct answer?
 ANSWER:
ANSWER:
You either remember the question inaccurately or a translation
has not been a very good one! I am guessing that the question should be
something like: When light passes into a medium where the velocity is
different, does the energy of the light change? The answer is no if
absorption is negligibly small. If it did change, where would the energy
come from or go to? The reason is best understood by thinking of light as
photons and the energy of each photon is hf where h is
planck's constant and f is the frequency of the light. The frequency
of the light in the medium is the same as outside. The wavelength, however,
does change because v=fλ where λ is the wavelength and
v is the velocity.
 QUESTION:
QUESTION:
A ball thrown upward has zero velocity at its highest point i.e no acceleration. The resultant of applied force and weight/gravity is also zero. Thus the body is at rest. Is it in equilibrium too? This is not a homework question. I and my friend are too confused.
 ANSWER:
ANSWER:
Right off the bat, your first sentence is incorrect.
Acceleration of something at rest is not necessarily zero. You cannot
determine whether an object is accelerating by knowing only its velocity
because acceleration is the way the velocity is changing which cannot be
known by simply knowing what the velocity is right now. In your example, the
ball is at rest right now but was moving upwards just before now and will be
moving down just after now. The ball has an acceleration which happens to be
9.8 m/s2; this means that one second before now it was moving
upwards with velocity 9.8 m/s and one second after now it will be moving
downward with velocity 9.8 m/s. It is not in equilibrium because Newton's
second law tells you that any object with a net force on it is not in
equilibrium; the only force (ignoring air drag) on the ball is its own
weight and this force is the source of its acceleration.
 QUESTION:
QUESTION:
A space craft travelling at very near light speed sets a course for a distant object.
So travelling at near light speed, could a navigation computer make corrections quick enough, and alter the trajectory for objects in its path. Could these calculations be made quick enough to miss the object?
Assuming computer calculations happen at the speed of light the craft could be on a collision course with an object before (a:) it saw it and (b:) before it could recalculate an evasive action missing the object.
With the added disadvantage that human thought isn't any where near quick enough to react to a blocking object.
So how could 'we' travel to distant objects without fear of ploughing into the first path crossing object?
 ANSWER:
ANSWER:
You raise an interesting and important question here. But it is
much worse than you think. For one thing, because of length contraction, an
object which an outside observer would see as being, for example, 1 light
year away from you would only be 1x√(1-.992)=0.14 light years
away as you observed it if going 99% the speed of light; that gives you a
lot less time to maneuver. But there is a much more important barrier to
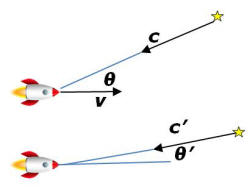
being able to navigate at very high speeds. The upper picture to the left
shows the space craft as seen by an outside observer; light from a distant
star comes with velocity c making an angle of θ
relative to your velocity v. But, if you now are on the space
craft, you observe the star at a different location specified by θ'
because of the velocity transformation to the new light ray c'.
Note that the magnitudes are the same, c'=c, but the directions are
different, θ'≠θ. It can be shown that θ'=tan-1[sinθ√(1-(v/c)2)/(cosθ+(v/c))].
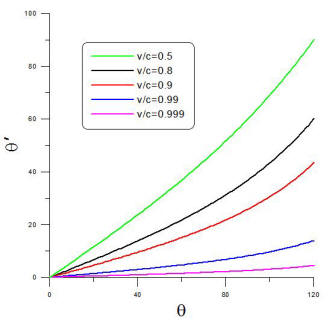
I have plotted this for several values of v to the right. The effect is
quite dramatic. For example, at 99.9% the speed of light everything in your
forward hemisphere and much from behind you will appear inside a 50
cone in front of you! Just having optics which could give good enough
resolution to see anything but an extremely bright light in front of you
would be a challenge in itself. But wait, it even gets worse! There will be
significant Doppler shifts and much of the light at very high speeds will be
shifted out of the visible spectrum. A nice little animated gif below (which
I found on
Wikepedia) demonstrates this but only up to 89% of
c.

 QUESTION:
QUESTION:
Since gamma rays are basically a form of light with much more energy than ultraviolet rays can they cause fluorescence in the same way as ultraviolet rays (black light)?
 ANSWER:
ANSWER:
The way fluorescence works is that the photon excites an
electron to a highly excited state which then deexcites by cascading down. A
gamma ray has so much energy that it the likeliest thing to happen would be
to completely knock out an electron, ionize tha atom which would then not
result in deexcitation. What then happens is that these energetic electrons
interact with atoms in their path, exciting them and then they deexcite by
emitting light. This is not the same as fluorescence and is called
scintillation. This is one of the main ways gamma rays are detected, by
scintillation detectors.
 QUESTION:
QUESTION:
Does mass affect kinetic energy?
 ANSWER:
ANSWER:
Of course. Classically the kinetic energy K=�mv2
where m is mass and v is speed. Relativistically, K=E-m0c2
where c is the speed of light, m0 is the mass of
the object when not moving, the total energy E=√(p2c2+m02c4),
and the linear momentum p=m0v/√(1-v2/c2).
So, you see, mass appears all over the place. The momentum of a massless
particle, the photon, is p=E/c; its energy is all kinetic, and
K=E=pc
since a photon has momentum even though it has no mass.
 QUESTION:
QUESTION:
Suppose two friends break their arm at the same time and a doctor says it will take both six weeks to heal. On the same day one friend is due to board a rocket that travels 99.999% speed of light. They have an uncanny ability to count in sync, in their heads. They agree to close their eyes and count up to six weeks, second by second.
The traveler only has to hit a reverse button once he counts exactly 3 weeks, and he'll return to the exact spot he left his friend.
After they have both counted six weeks in their heads, they open their eyes...
Is the traveler back with his friend??
The friend who did not travel finds his arm has healed. Has the travelers arm also healed??
The obvious answer is yes to both. The traveler has traveled at the same speed one way as far as the other (counting 3 weeks each way).
The traveler has counted the same amount as the non-traveler (3,628,800 seconds) so therefor his arm should be healed.
Special relativity would suggest his arm has not healed.. it would suggest a lot less than 6 weeks has passed for him! It suggests that not only time slows down, but the travelers mind
& body slow down too...does he count more slowly in his head? Does his breathing slow down also? Wouldn't he die from breathing so slowly??!!
 ANSWER:
ANSWER:
You have this a bit muddled. Let us first find out how far d'
the traveling friend travels in 3 weeks (as measured by him). d'=vt'=0.99999c∙3=2.99997c
or d'=2.99997 lw each way (1 lw is a light week, the distance light
travels in 1 week). The earth-bound friend, however, sees a much longer
distance that his friend has traveled because the friend sees the distance
length-contracted by a factor √(1-.999992); so the distance which
the earth-bound friend sees is d=2.99997/√(1-.999992)=670.8
lw each way; the time someone traveling 0.99999c takes to go this distance
out and back is 2x670.8/0.99999≈1342 weeks. The earth-bound friend has been
healed for about 1336 weeks, more than 25� years, when his friend returns
with a just-healed arm. You still cannot really accept that moving clocks
really do run slowly, can you?!
 QUESTION:
QUESTION:
I am currently doing a research paper on the perfect free-kick, could you
find an equation that suits the following variables? The soccer ball is
kicked from the origin of a coordinate system with an unknown velocity such
that it passes through the points (x,y)=(9.15
m, 2.25 m) and (x,y)=(22.3 m, 2.22 m). How can I find the magnitude
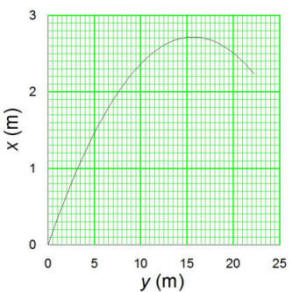
and direction of the initial velocity? Just having an equation to help me work with would be very nice.
 ANSWER:
ANSWER:
The equations of motion for a projectile which has an initial
velocity with magnitude v0 and angle relative to the
horizontal θ are x=v0xt and y=v0yt-�gt2
where v0x=v0cosθ, v0y=v0sinθ,
t is the time, and g=9.8 m/s2. Solving the x-equation
for t, t=x/v0x; putting t into the y-equation,
y=(v0y/v0x)x-�g(x/v0x)2.
Since you have two (x,y) data points, you have two equations with two
unknowns, (v0x,v0y). The algebra is
tedious, but the result is that v0x=21.0 m/s and v0y=7.30
m/s; v0=22.2 m/s, θ=19.20. To check my
answer I drew the graph shown to the right (note the different x and y
scales); it looks like my solution passes pretty close to the data points.
 QUESTION:
QUESTION:
Do physicists believe that some quantum events are truly random in the sense that they are unpredictable even if we had a computer that had complete knowledge of the universe? Or is it that they are considered random because there's no way of measuring the events due to a lack of measuring tools?
 ANSWER:
ANSWER:
Random is not the same as unpredictable. You cannot predict any
outcome of anything precisely; you can predict the probability that your
measurement will get a particular value�that is essentially what quantum
mechanics does. Essentially, the reason you cannot predict any outcome
precisely is that "complete knowledge of the universe" is impossible by a
computer or anything/anybody else. Even complete knowledge on one particle
is impossible.
 QUESTION:
QUESTION:
We have a theoretical minimum temperature, Kelvin's absolute zero. Do we have a theoretical maximum temperature, If so, what is it.
 ANSWER:
ANSWER:
See an earlier answer.
 QUESTION:
QUESTION:
Why do I WEIGH the same at the earths pole as I do at the equator ?
Given the earths radius 6378km and i'm doing 1600km/h and my MASS is 100kg thats about 3.1Nm/s of force trying to throw me off the ground.
YET
At the pole i still have 100kg MASS and the earths gravity hasn't changed ...whats the deal ?
 ANSWER:
ANSWER:
As anyone who follows my answers can tell you, I am very rigid
about what weight means. To me, my weight (on earth) is the force which the
earth exerts on me. A minority of text-book writers like to define weight to
be what a scale reads. There is one main reason why your weight is different
at the poles and equator: the earth is not a sphere but is slightly oblate
which means that you are closer to the center of the earth if you are at the
poles and so you are slightly heavier there. The figure to the left shows
equipotential surfaces for an oblate spheroid (much more oblate than earth)
and the ratio of the weights at the pole and the equator is 1.52/1.14=1.33.
There is an additional reason why a scale reads differently: because of the
earth's rotation, there is a centrifugal force at the equator which results
in a scale reading less than at the poles. If you take into account that the
earth is not really a uniform mass distribution, this can also affect the
local value of g. All of these are very small effects on earth. I
guess the bottom line to my answer is that you do not necessarily weigh the
same anywhere on the surface of the earth as anywhere else. Your mass is
always the same, though.
 QUESTION:
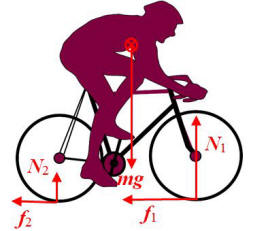
QUESTION:
As when sudden brakes are applied during riding a fast moving bike the back wheel leaves the ground. Why? Also what must be the conditions for the wheel
to not leave ground and when bike semicirculy revolves?
 ANSWER:
ANSWER:
To the right is the "free-body diagram" showing the pertinent
forces if the back wheel has not left the ground. The weight mg acts
at the center of gravity of the bike+rider and each wheel has a normal force
(N) and frictional force (f) from the ground. The bike has an
acceleration a in the direction of the frictional forces, so f1+f2=ma.
The system is in equilibrium in the vertical direction, so N1+N2-mg=0.
The bike is also in rotational equilibrium so all the torques about any axis
must be zero; summing torques about the front axle, Rf1+Rf2+DN2-dmg=0
where R is the radius of the wheel, D is the distance between
axles, and d is the horizontal distance between the front axle and
the center of gravity. Now, suppose that the rear wheel is just about to
leave the ground; then N2=f2=0.
The three equations then become N1-mg=0,
f1=ma, and
Rf1-dmg=0.
Putting the second equation into the third and solving for the acceleration,
a=g(d/R); if you are slowing down any faster than this,
your rear wheel will lift off the ground and the bike will no longer be in
rotational equilibrium. If a is really big, you will keep rotating
until your center of gravity is forward of the front axle; then you will not
be able to stop the bike from rotating all the way over and crashing you on
the ground. This actually happened to me once when I was mountain biking
with my son and I broke a couple of ribs! I do not understand your second
question.
 QUESTION:
QUESTION:
If I shine a light it emits a light particle outwards. Assuming it is travelling in vaccum all the way out and hits no light absorbing medium.
The farther it travels it starts losing energy and shifts to the red. Now how long in Earth years will it take for that photon particle to lose "ALL" its energy. How far will it travel in distance (light years) and what happens to that particle at the end of it all.. i.e it just cannot "disappear" or become void or null.
Or perhaps it will all be converted to some other form of energy but then what would it lose its energy to given it was hypothetically travelling in a vaccum/void all the way out?
 ANSWER:
ANSWER:
Let's first consider the particle to be a ball. If you throw it
up it will begin immediately losing energy and eventually stop. You can now
think of the earth as having acquired the energy the ball had, now in the
form of potential energy. Being a ball, it then falls back and extracts all
its energy back. However, if you throw the ball hard enough it will keep
going forever and the farther away it gets, the less energy it loses,
essentially moving with constant speed when it has gotten pretty far away.
The same is true of a photon, as you note, except for two important
differences: it cannot stop and it has no mass, just pure energy. The red
shift you refer to is the gravitational red shift and as the photon becomes
redder it is, as you stated, losing energy (also to the mass it is leaving)
but not speed. For the earth (and almost every object in the universe) the
effect of gravity is insufficient to ever cause the photon to lose all its
energy. Only black holes can rob a photon of all its energy; if a photon is
inside the event horizon of a black hole, as it tries to escape it gets
"redder and redder" until it has finally lost it all and it disappears. The
energy it had will now be found in a slightly increased mass of the black
hole.
 QUESTION:
QUESTION:
My husband is employed as a school bus driver. He repeatedly tells the middle and HS students not to stand in the aisle until the bus comes to a complete stop. He tries to explain to them (without knowing the exact physics behind it) that if they're standing while the bus is moving at say 40 mph, and he has to stop short for some reason, they will not be able to stop their bodies from propelling forward. They never seem to "get it". How can he explain this from a physics point of view that they might better "get"?
 ANSWER:
ANSWER:
Are you kidding? You actually think a bunch of rowdy kids is
going to listen to a physics lecture on the bus? If you want a detailed
description of the physics of this exact situation, I have given it in an
earlier answer. Here is a
suggestion which will maybe work: take a tall box with little width, maybe 5
feet tall and 1x1 feet at the base. Have everyone in the bus sit down and
have one student stand the box in the center of the aisle when the bus is
moving at about 40 mph. Have your husband then stop abruptly (not so quickly
that the sitting students might hit their heads) and watch what happens to
the box. Better yet, get a mannequin to stand in the aisle. You could also
put a little cart with wheels in the aisle which would go zipping to the
front of the bus when it stopped. The physical principle is inertia: an
object in motion tends to stay in motion unless acted on by some force (like
if you were holding on to something).
 QUESTION:
QUESTION:
Why is a flame hot? Where does its temperature come from?
 ANSWER:
ANSWER:
You first have to ask what temperature is for a gas: it is the
average kinetic energy per molecule. Put into everyday language, the higher
the temperature, the faster the average molecule in the gas is moving. The
presence of a flame indicates that some kind of chemistry is going on. The
simplest thing going on in a typical fire is that carbon (C) is combining
with oxygen (O2) to produce carbon dioxide (CO2). When
any chemical reaction occurs, energy is either released or you must add
energy to make it happen. When carbon dioxide forms, energy is released and
this energy shows up as the kinetic energy (speeding up) of the molecules in
the hot flame.
 QUESTION:
QUESTION:
Can an object become dead still in space and how would you know?
 ANSWER:
ANSWER:
There is no such thing as "dead still". Newton's first law or
the principle of relativity essentially proclaim that the laws of physics
are the same in all inertial frames of reference. There is no experiment you
can do which can distinguish which of two frames moving at constant velocity
relative to each other is at rest.
 QUESTION:
QUESTION:
A person is standing on a platform. Below him is another person, not wearing a hard hat. The person on the platform drops a standard sized marble. Approximately how high would the platform have to be in order for a marble to cause trauma/injury?
 ANSWER:
ANSWER:
This is a little tricky because there is no such thing as a
"standard sized marble". I figured an average marble would have a diameter
of about 1 cm (R=0.5 cm=0.5x10-2 m) and a mass of about M=1 g=10-3 kg. The second tricky part is that I do not know
how fast a marble needs to be going in order to penetrate the skull which is
how I would judge whether serious injury resulted. I do know that a bullet
which has roughly 10 times the mass of a marble will penetrate the skull at
a speed of about 60 m/s (about 130 mph). So, I would conclude that a marble
would have to be going quite a bit faster to penetrate the skull since it
would bring in a lot less momentum than a bullet with the same speed. So the
first question I will ask is what will be the speed if I drop it from a
height of h=5 miles (about 8000 m). Now, if you were just going to do
a simple introductory physics problem you would say "neglecting air
friction" the time to fall would be about t=√(2h/g)=√(16,000/10)=40
s and the speed at the ground would be about v=gt=10x40=400 m/s
(about 900 mph); I would guess that would do some serious damage! But wait!
It would be a really big mistake to say that air friction was negligible for
something going 900 mph. The drag on a falling object in air depends on how
fast it is going and can be approximated as F≈�Av2
(all quantities must be in SI units) where A=πR2≈2x10-5
m2 is the cross sectional area. When the drag is equal to the
weight, F=mg≈10-2 N, the marble will stop accelerating and
continue falling with the terminal velocity, vt=√(4mg/A)≈45
m/s (about 100 mph). So, since 45 m/s is much less than the 60 m/s necessary
for a bullet to penetrate the skull, I am guessing that no matter how high
you drop the marble from, it will not cause truly serious injury�it's going
to hurt though!
 QUESTION:
QUESTION:
Some people believe that because we are about 70% water that the moon and the sun have some force upon us ( gravitational and electromagnetic), similar to the ocean. Scientifically, is there evidence that can support this?
 ANSWER:
ANSWER:
Water has nothing to do with it. The reason you are aware of the
influence of the moon and sun on water is the tides; that is evident because
the ocean has a lot of mass and it is easier to pull it up than, for
example, to pull up a mountain. Nevertheless, there are forces on you
because you have mass and anything with mass will experience a gravitational
force from another object which has mass. Suppose that your weight is 150
lb�your weight is the force which the earth's gravity exerts on you. The
moon exerts a force of about 0.0005 lb and the sun exerts a force of about
0.09 lb on you. Even though the moon is much closer, the sun is much more
massive. There is no signfiicant electromagnetic force on us due to the moon
and sun.
 QUESTION:
QUESTION:
I have a question about light. If I am moving toward a source of light, why is it that the measured speed of said light is always constant? I've heard that motion is only relative with particles that have mass, but if I'm going half the speed of light towards a photon that's coming toward me, then why wouldn't I measure the photons speed as half the speed of light?
 ANSWER:
ANSWER:
I have answered this questions many times. See the
links my FAQ page and the links in
those links.
 QUESTION:
QUESTION:
As gas molecule come at rest at absolute zero temperature which is impossible to achieve and also kinetic energy depends on temperature then how is solid ice is formed
 ANSWER:
ANSWER:
Molecules in a solid are not at rest, they are vibrating like
masses on springs. As the gas cools, its molecules slow down and eventually
the speed is sufficiently slow that if one molecule collides with another
they will bind together. Eventually more and more bind together making the
solid.
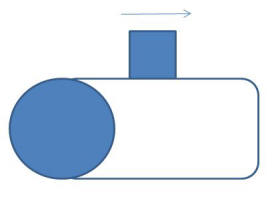
 QUESTION:
QUESTION:
Here is the scenario. I have a A volt motor that supplies B watt
to work. I connect the motor to a circular disc of R radius that is of M
mass and has a density of 1 unit. I want to use the motor to move a conveyor
belt of mass N. I will place an object of mass K on the conveyor belt. Is it
possible to find the velocity of which the object will be moving at given
the voltage? Or perhaps can we find the minimum about of voltage that is
needed to move the object. Assume that the efficiency of all the motor as
well as the whole thing is 100% and that frictional force and air resistance
can be neglected. You can add othervariables in either.
 ANSWER:
ANSWER:
This is an engineering problem, not physics.
However, it sounds to me like there is no answer if you have no frictional
losses because the motor will just keep adding energy to the system and
there is no loss.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
However, it should be able to work since the motor is attached to a conveyor belt, yes it will keep going but it will kep moving the conveyor belt only.
 ANSWER:
ANSWER:
If the motor is adding energy (B watts would mean B Joules of energy per second are being added) and there are no losses, where is that energy going? It will constantly accelerate the conveyer belt.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Is it possible to find the acceleration of the conveyor belt?
 ANSWER:
ANSWER:
Yes! Refer to the picture above. Suppose the mass and the
conveyor belt move with speed V; then the angular velocity of the
disc is ω=V/R. The moment of inertia of the disk is I=�MR2.
The kinetic energy of the belt plus mass is KE1=�(K+N)V2
and of the disc is KE2=�Iω2=�MV2,
so the total kinetic energy is KE=�(�M+K+N)V2.
The rate of change of the kinetic energy is equal to the power B, B=(�M+K+N)V(dV/dt)=(�M+K+N)Va
where a is the acceleration. Solving, a=B/[(�M+K+N)V]≡C/V.
Note that when V=0, a=∞; this just means that the motor cannot
deliver power unless it is actually spinning with some rate. But, as soon as
it gets moving it will have a very large acceleration which decreases as the
speed gets bigger and bigger. So, if you are really interested in such a
system, you will have to determine energy losses and probably also have a
motor with an adjustable power output. (Also, note that the voltage has
nothing to do with it, all you need is the power output.)
 QUESTION:
QUESTION:
What causes the universe to expand?
 ANSWER:
ANSWER:
For a long time it was assumed that the expansion was simply the
result of inertia achieved in the big bang�something that explodes sends its
pices flying apart. More recently it has been discovered that the expansion
is actually accelerating which implies some repulsive force is pushing out
as well; this is generally referred to as
dark energy.

 QUESTION:
QUESTION:
Could you explain why an electron in a stable orbit around a nucleus does not emit electromagnetic waves or photons. It only emits when the electron changes from a higher energy orbit. In a stable orbit the electron still is moving around so why doesn't it create a changing E field and radiate? Thanks, Paul
 ANSWER:
ANSWER:
The glib answer is simply that that is the way nature works.
Here we encounter an example of how we should not extrapolate the behavior
of something from a regime with which we have experience (for example,
accelerating electrons in a transmitting antenna) to regimes where we have
no experience (for example, tiny atoms). At the scale of atoms, the
wave-like properties of electrons become important and quantum mechanics
must replace Newtonian mechanics; when you solve the problem using the
correct mechanics, stable orbits occur naturally. I find the easiest way to
understand this qualitatively is to note that in an atom a stable orbit is
one in which the wavelength of the electron is just right to form a standing
wave in its orbit as shown to the right (de
Broglie's picture of the Bohr atom).
 QUESTION:
QUESTION:
Say I have a simple bar magnet that I hold in my hand vertically. If I move the magnet side to side in a sinusoidal motion am I transmitting electromagnetic waves propagating at the frequency of the movement?
 ANSWER:
ANSWER:
Yes. The radiation is primarily
magnetic dipole radiation.
 QUESTION:
QUESTION:
I've read that in circular motion things move in a circle because of the centripetal force, and that the direction of acceleration is towards the center for this reason. Now my question is that why don't things actually move towards the center of the circle if there is an unbalanced force directed there and an acceleration in the same direction
 ANSWER:
ANSWER:
Because "accelerate" is not synonymous with "move". For another
example, when a ball is moving vertically up its acceleration is vertically
down. The problem is that in everyday life we associate the word accelerate
with speeding up but in physics acceleration is the change of the velocity.
Velocity is a vector, a quantity which has both magnitude and direction, so
there are two ways you can change it�change its magnitude or change its
direction. If the force happens to be parallel to the velocity, the object
speeds up. If the force happens to be antiparallel to the velocity, the
object slows down. If the force happens to be perpendicular to the velocity,
the object changes its direction without speeding up or slowing down; that
is what happens in uniform circular motion. If the force happens to be at
any other angle to the velocity, the object changes both magnitude and
direction.
 QUESTION:
QUESTION:
If you have two weights, where one is 100 grams and the other is 200 grams and you use the same spring to create a pendulum with them (one at a time) why isn't the amplitude the double for the heavier weight?
(This is the result of an exercise we did, my personal curiosity, and my teacher's unwillingness to explain
because he says it's too complicated for our level.)
 ANSWER:
ANSWER:
I think you must surely mean a mass on a spring oscillating
vertically, not a pendulum. That is what I will assume. You have probably
not studied energy yet which is why your teacher did not want to get into
it. Energy methods are, by far, the easiest way to answer your question
which is what I will do. Two things you need to know: potential energy of a
spring which is stretched by an amount y is �ky2
and gravitational potential energy of something a distance y above
where y=0 is mgy. Imagine taking a mass m and attaching
it to a spring with spring constant k which is unstretched and
holding it there for a moment. Where it is right now I will define to be y=0 and so, since the spring is unstretched, the total energy of the
system is �k∙02+mg∙0=0;
the energy never changes. As it falls it speeds up for a while and then
slows down for a while (acquiring and then losing what is called kinetic
energy, energy by virtue of motion), finally stopping and going back up.
If it has fallen some distance A (for amplitude) before turning
around, the energy is now 0=�kA2+mg(-A)
and so we find two solutions (it is a quadratic equation), A=0 (we
already knew it was at rest there) and A=√(2mg/k). So,
you see, the amplitude is proportional to the square root of the mass, not
the mass. (Incidentally, most folks would call the amplitude of this
oscillation to be �A. I thought it would be clearer this way.)
 QUESTION:
QUESTION:
So, objects with energy give off some sort of radiation, some visable some not, and in higher energies and heats, the wavelengths get smaller. Can there be something so hot that the wavelength is smaller than a plank length?
 ANSWER:
ANSWER:
First of all, there is absolutely no proven significance of the
Planck length, it is simply a combination of three fundamental constants, G,
c, and ħ, which has the dimension of length, √(ħG/c3)=1.6x10-35
m. And, you should not think of just fast or hot as being the source of
photons (electromagnetic radiation) because it is energy change, not energy
itself, which can result in radiation. There is no physical law that I know
of which would forbid a photon with wavelength shorter than the Planck
length. I should point out, though, that astrophysicists have difficulty
coming up with models for how the most energetic cosmic gamma rays observed
could have been created and they have wavelengths much longer than the
Planck length.
 QUESTION:
QUESTION:
I came across a particle table one day, and I'm wondering why the amu for an element is constant. From my understanding, a proton is formed by two up quarks and a down quark but there are other particles that have the same charge as the up/down quarks but with different masses(stange,charm,top,bottom). And why can't tau and muon particles replace electrons since they also have the same charge as an electron.
 ANSWER:
ANSWER:
Regardless of what something is made of, if it is stable it has
a definite mass. Muons and taus are not stable particles and so atoms
with them replacing electrons are not going to appear in nature.
Muonic atoms
have been made but survive only fleetingly before the muon decays. I have
never heard or a "tauic atom", probably because it has a much shorter
lifetime than a muon and cannot therefore be made in copious amounts.

 QUESTION:
QUESTION:
In looking at the photgraphs from the Rosetta comet mission, I notice what seems to be "loose boulders" on much of the surface. How much gravitational attraction does that comet have? Is it enough to keep the boulders on the surface as it would on Earth, or are the loose parts of the comet simply in a coinciding orbit?
 ANSWER:
ANSWER:
If they remain in the same place relative to the main body of the comet they are resting on the surface. If they were moving alongside, there would be an attractive force which would bring them together;
otherwise, to remain separated, the boulder would have to be orbiting the
main body. I once answered a question which surprised me�two
dice, in empty space and separated by 10 cm, take only about 8 hours to come
together.
 QUESTION:
QUESTION:
How long would it take for a rocket ship travelling at 100 times the speed of sound to reach the nearest star which is at 3.8 light years away?
 ANSWER:
ANSWER:
Take the speed of sound to be about 300 m/s. Then the speed of
the ship would be about v=3x104 m/s. Since the speed of
light is about c=3x108 m/s, v/c=10-4
and so relativistic effects need not be considered. The time would then be
about 3.8/10-4=38,000 years.
 QUESTION:
QUESTION:
If like in the movie " Armageddon", a giant meteor were to be heading towards the earth, lets say a moon sized meteor moving at well over the speed of sound, assuming that this would wipe out the planet on impact, how much force do we need to completely annhilate it? Or at least render it harmless? Is the force required equal to F=ma , that is an equal and opposite force capable of destroying the planet on its own? Or something far less, capable of destroying the meteor with lesser mass is all thats required?
 ANSWER:
ANSWER:
To destroy the meteor completely requires a lot of energy. The
energy to blast apart a uniform sphere of mass
M and radius R
is U=3GM2/(5R).
For the moon, U=2.5x1031 J. Suppose that to just blow it
to small pieces rather than total dust took a billion times less energy;
then the energy would be on the order of 1022 J. The energy of
the Nagasaki bomb was about 1014 J, so you would need about
10,000,000 of them. Clearly, it is hopeless to obliterate a moon-sized
object. Better to catch it early and deflect it by a small angle which would
be adequate to avoid collision. It would still take a good amount of energy
for an object as massive as the moon, though.
 QUESTION:
QUESTION:
If I am at a point in space where very, very, very little gravitational pull exists, what happens to the time clock on my spaceship as opposed to clocks on earth?
 ANSWER:
ANSWER:
A clock in a gravitational field runs slower.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
What I am asking, if you were at a point in space, where the gravitational forces were almost 0, would your clock, in your space craft be running extremely fast as observed from earth?
I was thinking about a spot in the universe were the gravitational effect
would be almost opposite of a black hole. Like the trampoline example you used on the web site. I set 5 or 6 bowling balls on the trampoline so each makes a dent. I then use a marble and find a spot to set it where it is not affected by the bowling balls. Now I know my ship is moving always towards some mass but there has to be a spot where gravitational effects all almost 0. Maybe that spot in space would be inaccessible to my ship, kind of an anti event horizon where I would not have enough power to get too. a spot where Light can not even enter.
I Know that my question is flawed, but I can't help to think about a black hole as a gravity pit, and that makes me think of a spot in space where there is a gravitational mountain (Anti-Black Hole, with an anti-Event horizon). In this spot time runs so fast as not to exist....
 ANSWER:
ANSWER:
First of all, all your thrashing around with black holes etc.
trying to find a spot with small gravitational field is totally unnecessary;
all that is required is that you need to be far away from any mass and
nearly the whole universe satisfies that criterion. We generically call such
places intergalactic space. So, choose some place, maybe halfway
between here and the Andromeda galaxy, our nearest galactic neighbor. For
all intents and purposes the field there is zero and a clock would run at
some rate. Now, take that clock and put it on the surface of a sphere of
radius R and mass M. The
gravitational time dilation formula you need to compute how much slower
the clock would tick at its new location is √[1-(2MG/(Rc2))] where
G=6.67x10-11
N∙m2/kg2 is the universal constant of gravitation and
c=3x108 m/s is the speed of light. Putting in the mass and
radius for the earth, I find that the space clock runs about 7x10-8
% faster than the earth clock, certainly not "extremely fast"! The
bottom line here is that, except very close to a black hole, gravitational
time dilation is a very small effect. An interesting fact, though, is that
corrections for this effect must made in GPS devices because they require
extremely accurate time measurements to get accurate distance measurements.
 QUESTION:
QUESTION:
My physics lecturer tried his best to answer my question on what exactly a spin in electron is.
But I couldn't understand. Besides he himself looked quite confused. So could you kindly help me out?
What is generally a spin of an electron? And how would I explain it to a layman?
 ANSWER:
ANSWER:
Take the earth as an analogy. Earth has two kinds of angular
momentumit revolves around the sun and it rotates on its axis. Angular
momentum refers to rotational motion of something. Its motion around the sun
is called orbital angular momentum and its spinning on its axis is
called intrinsic angular momentum. Now think about an electron in an
orbit around a nucleus in an atom. It clearly has orbital angular momentum
because of its orbit. But it also has intrinsic angular momentum, that is,
it behaves in many ways as if it were spinning on its axis; this is usually
referred to simply as spin. This is a fine analogy, but it should be
emphasized that spin is not really such a simple classical concept. For
example, if you were able to exert a big enough torque on the earth you
could stop its spinning or make it spin faster. The spin of an electron is a
constant property and cannot be changed. You can change the direction
(clockwise or counterclockwise) but not the magnitude of spin. Also, if you
try to model the electron as a little spinning sphere to find out how fast
it is spinning, you get absurd, unphysical answers. So, you can only push
the electron/earth analogy so far. Finally, I should note that in
relativistic quantum mechanics (Dirac equation) the existence of electron
spin is predicted to be exactly what it is measured to be.
 QUESTION:
QUESTION:
I intend to heat a sealed tank to 280 degrees fahrenheit to cook lumber. I would like to be able to keep the pressure at a contsant 40-50 psi inside the tank. I need to know how much the pressure will increase inside the tank as I add the heat. I don't want the tank to blow up on me while it's being heated. I plan on using heating elements inside the tank. If needed I will also add pressure to the tank to get to 40-50 psi.
 ANSWER:
ANSWER:
The operative principle here is the ideal gas law, PV=NRT
where P is absolute pressure, V is volume, N is
the amount of gas, T is absolute temperature, and R is
a constant. The pressure numbers you gave are, I assume, gauge pressure, the
amount above atmospheric pressure which is about P1=15 psi, so
your target absolute pressure range is P2=55-65
psi. The temperatures must be converted to kelvins (K), absolute
temperature: I will take room temperature T1=700F=294
K and T2=2800F=411 K. This is all we need to
know to find the final pressure assuming V, N, and R do
not change: P=P1(T2/T1)=15(411/294)=21
psi. This is well below your target pressure. Probably the easiest thing to
do is to increase the pressure before you heat it by pumping in
room-temperature air. Suppose you want a final pressure of about 60 psi (45
psi gauge pressure), then the room-temperature pressure you should start
with should be P1=60(T1/T2)=P1=60(294/411)=42.9
psi=27.9 psi gauge pressure.
All this assumes that your tank is strong enough to take these pressures and
I cannot guarantee that. I strongly suggest that you be certain you have a
pressure guage on the tank as well as a pressure relief valve which will
keep the pressure from getting too high.

 QUESTION:
QUESTION:
What frequencies of light or radiation will petroleum jelly absorb. What is happening at the nuclear level when petroleum jelly adsorbs light from a black light and turns it into visible light.
 ANSWER:
ANSWER:
Your first question is far too broad to answer here. If it
really matters to you, you can get a lot of information
here. The second
question is easier to answer with a qualitative answer. First, nothing goes
on at the "nuclear level", it all happens at the atomic or molecular level.
Ultraviolet light has enough energy to excite the electrons in the molecules
to a very high excited state; then, rather than dropping back down to the
ground state, they cascade down through many levels emitting many much less
energetic (longer wavelength) photons which happen to be in the visible
range. The picture to the right is a smiley face made of petroleum jelly and
illuminated by a black (ultraviolet) light. This phenomenon is called fluorescence.
 QUESTION:
QUESTION:
How fast would a more massive planet than Earth, say twice as massive, with the same diameter have to spin to produce an Earth-like sense of gravity, due to centripetal force, at its equator? Might there exist a massive Earth-like planet, environmentally speaking, that we could still live on because its spin negated its gravitational pull enough to produce an Earth-like sense of gravity that wouldn't crush us?
 ANSWER:
ANSWER:
Let's just do it in general, the pseudo-earth being N
times more massive than our earth. The apparent weight at the equator would
be Nmg-Fc=mg
where Fc=mv2/R=mRω2
is
the centrifugal force. Solving, ω=√[(N-1)g/R]
where ω is the angular velocity in radians per second. For example,
if N=2, ω=√[g/R]=√[9.8/6.4x106]=1.24x10-3
s-1=2π/T where T is the period. So, T=5.08x103
s=1.41 hours.
 QUESTION:
QUESTION:
Consider two identical coins placed one over the other. Now the force of gravitation acting between them should be infinte as gravitational force varies inversely to the distance between their centres which is very very small so force of gravitation between them should be infinite and we couldn't be able to separate the two bodies. But it is not true we easily separate them. So basically what is mistake/error that
I have made?
 ANSWER:
ANSWER:
First of all, very small does not mean zero. The force will
certainly not be infinite. Let's do an approximate calculation for two US
pennies, mass of 2.5 g=2.5x10-3 kg, thickness of 1.52 mm=1.52x10-3
m. So their centers of mass are separated by 1.52x10-3 m. I will
treat them as point masses at their centers since an exact calculation would
be pretty complicated and I just want to demonstrate that the force will
certainly not be infinite. The force of gravitational attraction is F=(2.5x10-3)2(6.67x10-11)/(1.52x10-3)2=1.8x10-10
N. The weight of each penny is 2.5x10-3x9.8=2.5x10-2 N.
 QUESTION:
QUESTION:
My question is one of curiosity regarding the LHC.
If I am correct, when you accelerate an object to relatively high speeds then the mass of the object increases.
As far as I know, at the LHC they are accelerating lead nuclei near the speed of light. My question is what is the mass/energy of these nuclei when they reach top speed? Mostly curious on something
I can compare it to on a classical scale. I understand that nuclei are very small and don't have much mass but with that amount of energy put into them
I would imagine that the impact is tremendous for their size.
 ANSWER:
ANSWER:
I have
previously worked this out for a relativistic proton at 99.99999999% the
speed of light. A lead nucleus would with this speed would have about 200
times the mass of a proton, so its mass would be about 2.4x10-20
kg; a baseball has a mass of about 0.15 kg. Since the mass of the lead
nucleus at rest is about 3.4x10-25 kg,
its energy is nearly all kinetic, K≈mc2=0.002 J; a 100 mph
fast ball has a kinetic energy of about �mv2≈150 J. As in the
earlier answer, the mass has increased by a factor of about 70,000 but
is still very tiny.

 QUESTION:
QUESTION:
I know that when electrons get excited they basically move further from the nucleus, but what happens when the nucleus itself goes into an excited state?
 ANSWER:
ANSWER:
Nuclear structure is more difficult to understand because,
unlike an atom, the main force felt by the nucleons (protons and neutrons)
is not from some central point but from their nearest neighbors. It was
therefore somewhat surprising to find that many aspects of nuclear structure
may be understood by considering the nucleons as moving in an average central potential and
in well-defined orbits, similar to how electrons in an atom move; this is
called the shell model of the nucleus. So one way to excite a nucleus is to
simply raise some particular nucleon to a higher orbit as happens in atoms.
These are called single-particle states or shell-model states. However,
nuclei may also be viewed as fluid drops which behave collectively, that is,
all the nucleons move together. Most nuclei are spherical and can be excited
simply by causing them to vibrate�imagine a liquid drop which is sloshing
around in a rhythmic way. The picture to the left shows the most common
shape vibration of nuclei, the quadrupole vibration; the original nucleus
(dot-dash line) oscillates between football-shaped (American or rugby) and
doorknob-shaped, passing through the spherical shape as it vibrates between
the two. Some nuclei are not spherical, usually football shaped, and these
nuclei may be excited by being made to rotate.
 QUESTION:
QUESTION:
When a string acting as a standing wave is plucked/oscillated at its fundamental frequency (like that of a guitar), is there a relationship between the amplitude of the string itself and the amplitude of the sound it makes. If so what exactly is it?
I know that the string will be a transverse wave while sound is a longitudinal wave, so im not sure how exactly to convert the amplitudes if there is a way to do so.
 ANSWER:
ANSWER:
Take a guitar string and connect it between two rigid points
(two granite walls, for example) and pluck it. You will hardly be able to
hear it at all. A guitar is a complex instrument and it is really the
vibration of the guitar itself and the air inside it that is mainly what you
hear�the string excites the guitar and it acts like an amplifier. The
response of the guitar to the vibrating string depends on the quality of the
guitar or else there would be no reason to have some guitars much more
expensive than others. So there is no simple relationship which you seek
between the amplitude of the string and the amplitude of the of the
resulting sound. I would think, up to a point, you could roughly estimate
that the two were proportional. However, you also have to factor in that a
guitar string does not vibrate with only the fundamental frequency but also
includes all the overtones and the guitar will
respond differently to the different overtones.
 QUESTION:
QUESTION:
Could an object theoretically achieve light speed if it were falling far enough for long enough? Since speed increases the closer a falling object gets to it's periapis, could an object with an apoapsis incredibly high and an incredibly low periapsis fall for long enough that it would reach speeds close or surpasing the speed of light?
 ANSWER:
ANSWER:
No object could ever reach the speed of light. See my
faq page for why not. No matter how
long a particle falls through a gravitational field, it can never reach the
speed of light. An earlier answer works out
the speed as a function of time for an object falling through a uniform
field. Classically, if you have two point masses they will accelerate toward
each other with ever increasing acceleration such that when they are
coincident their speeds will be infinite. But when either of their speeds
become comparable to c
they are no longer classical and their speeds will approach c
instead. Also, there is no such thing as a true point mass.
 QUESTION:
QUESTION:
From a spaceship that moves away from you very quickly (say 0.33c), a "photon" is emitted when the spacecraft clock marks the time t0 and a length measurement performed on the ship tells your distance is 1 light year.
How long does the photon to reach you? with times measured by you and by the ship?
 ANSWER:
ANSWER:
The distance from you to the ship, as measured by you, at the
time the photon is emitted is 1/√(1-.332)=1.06 ly and so the time it takes to reach
you is 1.06 yr. An observer on the ship says it takes 1 yr.
 QUESTION:
QUESTION:
Suggest that we have constructed a model of the solar system by
decreasing the sizes of all orbits by n = 0.005. We have kept the average
density of the planets and that of the Sun the same as in the original solar
system. How will the periods of rotations of planets change in our model?
 ANSWER:
ANSWER:
Is this homework?
Are the sizes of the planets also scaled by n?
 QUESTION:
QUESTION:
No this is not homework-it was in a past paper and I was curious as to how to answer it!
And the question does not say, although I assume so!
 ANSWER:
ANSWER:
The period T of an elliptical orbit with semimajor axis
a around a body of mass M which is much bigger than the mass
of the orbiting body is given by T=2π√[a3/(GM)]
where G is the universal gravitational constant 6.67x10-11
N∙m2/kg2. So the answer to the question depends on how
the masses are scaled. If all the masses stay the same, the new periods T' are simply scaled by √0.0053=3.54x10-4. If the
densities remain the same and the sizes of the sun and planets themselves
are also scaled down by 0.005, then the masses will scale by the factor M'=0.0053M
because the mass is the density (unchanged) times the volume
(proportional to the cube of the radii). Therefore the periods would remain
unchanged, T'=2π√[(0.005∙a)3/(G∙0.0053∙M)]=T.
 QUESTION:
QUESTION:
I measure 179cm in height and exert 194lbf on a scale. If I were to gain 61cm in height and keep the exact same body proportions in relation to the height I have now, how much force would I exert on the scale?
(This is not homework. I'm an author. I did some math myself, and came up with a factor of about 2.4 for the weight increase, but I wanted a professional opinion.)
 ANSWER:
ANSWER:
If all dimensions of an object increase by a factor N,
the volume increases by a factor N3. In your case N=(179+61)/179=1.34,
so the volume increases by a factor of 1.343=2.41. Assuming that
the density of all body parts remains constant, the weight would then be 468
lb. Looks like you nailed it!
 QUESTION:
QUESTION:
How we can describe formation of a stationary wave in open organ pipe? How
is the wave reflected at the open end?
 ANSWER:
ANSWER:
It is a property of all waves that, when the medium in which the
wave is traveling changes its physical properties, reflection can happen.
The properties of the air certainly changes at the open end�it is contained
inside a tube inside and not constrained outside.
 QUESTION:
QUESTION:
Why is uranium the most common element used in nuclear fission?
 ANSWER:
ANSWER:
It is the only naturally occuring
fissile
nucleus.
 QUESTION:
QUESTION:
Which scale in temperature is larger?
For example, in terms of distance we have meter and kilometer
1 km=1000 m,
so km is larger than meter. In terms of temperature,we have celcius and kelvin
273k=0 C,
373k=100 C. By similar concept i may say celcius is larger than kelvin.
But I'm told by my teacher that the conversion formula suggests kelvin is a larger scale.
So which is a larger scale?
 ANSWER:
ANSWER:
Your confusion is that you do not define carefully what you mean
by "which scale�is larger?" For example, you say that, for scales of
distance, a kilometer is larger than a meter which is certainly true; but in
any given length there are more meters than kilometers so you could say that
the meter gives a bigger number than the kilometer does. I prefer the first
definition whereby you compare the sizes of the units. For temperature, 1 K
is exactly equal to 10C, so both you and your teacher are
wrong�the scales are the same. In terms of magnitude, though, the
temperature of something measured in Kelvins is always a larger number than
if measured in degrees Celcius.
 QUESTION:
QUESTION:
When I was young my father had a glass of water from our well that never froze at -40 degrees Farenheit? What else was in the water that would make this happen?
 ANSWER:
ANSWER:
Did your father have a still in the well house? Sounds like
grain alcohol to me, freezing point -1730F.
 QUESTION:
QUESTION:
We know in mechanics that F=ma. But then in electric fields force on a charge is given by Coulomb's law. Both are forces. What bothers me is that can they be shown to be the same in a way. Like is there a way to compare them? I'm just confused about this.
 ANSWER:
ANSWER:
F=ma, Newton's second law, is telling you what happens if
you exert some force F on some mass m; you should maybe think
of it as a=F/m. Coulomb's law tells you what the force is between
two point charges, F=kq1q2/r2.
You could now examine the special case of charge q1 which
happened to have a mass m1 and be a distance r from
charge q2: it would have an acceleration a=kq1q2/(r2m1).
 QUESTION:
QUESTION:
Two people are on a high speed, constant velocity train on opposite ends. One person standing on the platform. The two people aim a laser beam at the center of the train at the same time in their reference frame. In the center of the train, there is a special gun that will shoot and kill whoever's laser beam reaches it first; but if the two beams reach it at the same time it will be disarmed. From the person on the platform's standpoint, one of them dies due to the relativity of simultaneity. From the two people on the train's standpoint, they both live. Later, the two people get off their high speed train and meet with the person on the platform. Is this not a paradox? The platform person clearly saw one of them die.
 ANSWER:
ANSWER:
The only thing that matters is what the "special gun" sees; it
is in the same inertial frame as the shooters, so it does not fire because the two pulses arrive simultaneously in
that frame. The guy on the side sees the pulses not arriving simultaneously but the gun not firing.
 CORRECTION:
CORRECTION:
It has been pointed out to me by John Disciullo that the above
answer is wrong. Here is his answer:
 ANSWER:
ANSWER:
I think the person on the side will see the lasers arriving simultaneously at the gun and disarming it. What will not be simultaneous to the observer on the side is both people shooting. He will see the person at the back of the train shooting first and the person at the front of the train shooting slightly afterwards. The laser shot from the back of the train, even though fired first, arrives at the same time as the one shot from the front since the special gun is moving away from the back laser pulse and towards the front one.
 QUESTION:
QUESTION:
All the electrons in an atom keep moving (vibrating) year by year from where they get this much of energy?
And why the energy does not finishes like our energy finishes after some time?
 ANSWER:
ANSWER:
When you say "�energy
finishes after some time�"
I suppose you mean like you have to fill up your gas tank in order to keep
your car moving. The only reason you have to do that is because friction is
constantly taking energy away from your car so energy is being lost. But
electrons in atoms do not experience friction and, once they are given
energy in the first place, the energy will never go away. Imagine a mass
hanging on a spring and subject to no friction; once you start it
vibrating (give it some energy), it will never stop.
 QUESTION:
QUESTION:
I am inside a train in which all the sides/windows are sealed i.e., I cannot see anything from inside. If the train moves in a friction-less rail, i.e., without jerking, how can I prove that there is motion taking place or there is displacement?
 ANSWER:
ANSWER:
There is no such thing as absolute velocity, so there is no way
you can determine if you are moving with a constant velocity. The principle
of relativity says that the laws of physics are the same in all inertial
frames of reference so there is no experiment you could devise telling you
what your speed is. If your train were on earth, then you would not be in an
inertial frame because the earth is curved and rotating and very careful
measurements could detect this, but I believe you meant that the train is
moving in a perfectly straight line and no earth motion effects.
 QUESTION:
QUESTION:
Is higher frequency really more energy?
It is thought that higher frequency has more energy. However, the higher the frequency the smaller the wavelength. With that said, though the higher frequency is delivering more energy to a a given location, it is giving less total energy in a given area. A lower frequency is giving less energy to a given location, but more energy in an area. So the TOTAL energy of the wave would seem to be equal. Greater area(wavelength), lower frequency. Higher frequency, lower area(wavelength).
 ANSWER:
ANSWER:
I am afraid your thinking is muddled. Electromagnetic waves of a
given frequency are a collection of particles called photons; the smallest
amount of electromagnetic wave you may have is a single photon which will
correspond to a particular frequency. The energy E of a single photon
is proportional to its frequency f, E=hf where the
proportionality constant h is Planck's constant. So if 1000 red
photons hit a wall and 1000 blue photons hit a wall, the blue photons will
bring the most energy.
 QUESTION:
QUESTION:
Is it possible to derive the formula for Kinetic Energy without using work? Or are they linked by definition?
 ANSWER:
ANSWER:
Well, I can tell you that you never have to utter the phrase
"work is defined as�" The work-energy theorem is merely the integral form of
Newton's second law. For simplicity, I will do this simple derivation in one
dimension. F=ma=m(dv/dt)=m(dv/dt)(dx/dx)=m(dv/dx)(dx/dt)=mvdv/dx.
Rearrange: Fdx=mvdv. Integrate:
∫Fdx=m∫vdv=�mv22-�mv12
where the integral on the left is from x1 to x2
and is usually called the work W. Generalizing to three dimensions,
∫F∙dr=�mv22-�mv12
where the integral on the left is from r1 to r2.
 QUESTION:
QUESTION:
How can we know the true mass of an object in space with no gravity? What's holding us back from moving at light speed without restrictions of gravity? From what I understand we should be able to reach light speed with a burst of energy that should be almost instantaneous.
 ANSWER:
ANSWER:
I will take "true mass" to mean rest mass. The mass m is a measure of the inertia, the resistance to
acceleration when pushed on by a force F. The relation is m=F/a
where a is the acceleration of m resulting from F (as
measured for velocities small compared to the speed of light); this is
Newton's second law. So if you push on the object with a known force and
measure the acceleration, you will have the "true" mass. Gravity has nothing
to do with how fast something can go. For a more detailed description
correct at higher velocities, see an
earlier answer.
 QUESTION:
(This question refers to an
earlier
answer.)
QUESTION:
(This question refers to an
earlier
answer.)
With respect to your
ANSWER above, I have read elsewhere that one of the observations from particle accelerator experiments is that the mass of a particle increases the more it is accelerated AND that there is a concomitant release of energy (I recall reading �release� vs expenditure or other terminology, but the ol� memory could be faulty, too). I read in your
ANSWER above about inertia being what increases versus size/"amount of stuff" as a given mass accelerates. Per my outside reading I am attempting to conceive the source of the energy released, not in mathematical terms, but with creative logic, if there is such a thing. Maybe not. Math might be the only way to explain the phenomenon. My attempt with English in question form: Is the measurable release of energy due to the fact that so much more energy is required to continue accelerating the particle? Is the source of the "released energy" I read about actually the instrument itself, the particle accelerator? For some reason, prior to reading your
ANSWER, I conceived that as mass/inertia increases [as acceleration takes place] there was some inherent energy in the particle itself that with the added force of acceleration, inevitably had to be expressed / released. Creative huh? What IS the source of that energy "released" as the particle accelerates and its inertia increases? Or am I so way off you�re having a cleansing, releasing, hearty laugh? And, can this concept be explained in language that an extremely uneducated but by no means unintelligent person can understand? Are you that good? I�m giving you lots of credit, much deserved for your dedication to askthephysicist. If answering requires math, my reading said answer is not likely to be helpful so save yourself the time and move on with your day.
 ANSWER:
ANSWER:
I have never encountered reference to such an "energy release"
by relativistic particles as they were accelerating. While the particle is
accelerating, the force accelerating it does work which increases the energy of the particle. The only math I will use here is
E=mc2 which I hope you can work with�this simply says that any particle
has an inherent energy due to is its mass m which is the mass (inertia) times the speed of light
c
squared. If a particle is at rest, it has energy because it has mass. If a
particle is moving, the classical view is that it also has what we call kinetic energy,
energy by virtue of its motion. There are two
ways you can look at it. One is that we observe that the mass m
increases as the particle speeds up, eventually approaching infinite mass as
the speed approaches the speed of light; in this view, kinetic energy is
simply folded into the quantity mc2. The other way is to
say that the particle has an inherent mass energy m0c2
where m0 means the value that m has if the particle is at
rest; in this view we interpret the energy of the particle to be rest mass
energy plus the kinetic energy K it has by virtue of its motion,
m0c2+K.
These are just two ways of looking at the same thing; therefore, if the
particle retains its identity, if it now interacts with its environment it
can release the energy it previously gained by accelerating and if it ends
up at rest it will have released K Joules of energy. Any energy this
particle "releases" can only come from energy which it previously acquired.
 ADDED
THOUGHT:
ADDED
THOUGHT:
An accelerated particle
does radiate electromagnetic energy (light, x-rays, etc.) called bremsstrahlung; this is how an antenna works. So, when a particle is
being accelerated, it does "release" a bit of energy in this way. The rate
of this radiation is usually quite small compared to the rate at which
energy is being added and is often ignored when considering accelerators.
That which you "read elsewhere" might have been referring to bremsstrahlung.
 QUESTION:
QUESTION:
How come when I suck on an empty glass bottle hard enough my lips get pulled into the opening of the bottle?
 ANSWER:
ANSWER:
When you remove air from the bottle, the pressure inside the
bottle is lowered compared to normal atmospheric pressure. It is the
atmospheric pressure on the outside which pushes your lips into the bottle.
 QUESTION:
QUESTION:
I hope this question is stupid and is a very quick answer. If i have an object submerged in a tank of water, say a solid cylinder, obviously the pressure at the top of the cylinder will be less than the pressure at the bottom of the cylinder, due to the difference in depth between the two points (P=pgh). What I would like to know is how this difference in pressure exerts a force on the cylinder, and where? Is the force acting on the bottom of the cylinder, trying to push it to the surface? I just can't wrap my head around this at all.
 ANSWER:
ANSWER:
Sorry to disappoint you, but your question is not stupid. You
have discovered Archimedes' principle. Since, as you note, the pressure at the bottom of
the object (pushing up) is greater than the pressure at the top of the
object (pushing down), there is a net push up. This force is called the
buoyant force. It may be shown that the buoyant force is equal to the weight
of the water displaced by the object. The buoyant force determines whether
an object floats (buoyant force greater than weight) or sinks (buoyant force
smaller than weight) and why swimming is sort of like flying.

 QUESTION:
QUESTION:
If a single seed can produce a huge tree then how can we say that the mass of the universe is constant?
 ANSWER:
ANSWER:
We can't say that the mass of the universe is constant; the
energy of the universe is constant. Every day, for example, the sun's mass
decreases because mass (hydrogen) is being turned into energy plus different
smaller mass (helium). In your example, the mass of the tree was not created
from nothing. The tree took water, carbon dioxide, and nutrients from the
soil and using energy from sunlight it built itself. All the mass and energy
are accounted for.
 QUESTION:
QUESTION:
If you have a space station with a 95 meter diameter gravity deck at one g what would the gravity be if you put another deck 9 meters above it?
 ANSWER:
ANSWER:
So the radius of your primary deck is 47.5 m and your secondary
deck has a radius of 56.5 m. The pertinent equation is
ω=√(a/R) where
a is the acceleration, R is the radius, and
ω is the angular velocity. For your
primary deck ω=√(9.8/47.5)=0.45 s-1.
The secondary deck has the same ω, so
0.45=√(a/56.5) or a=11.7
m/s2 which is about 19% larger than g=9.8 m/s2. I should point out that since a person has a size on the
order of 2 m, this will not be a very comfortable environment since the
gravity at your head would probably be noticably different than at your
feet.
 QUESTION:
QUESTION:
I came across your site while looking for the answer of a physics problem I would like to program in a Smartphone app.
A toy car is dragged from position A to B giving it an initial velocity (v=d/t). At point B the car is released where it travels in a straight line until the frictional force of the ground stops the toy car completely (position C). I would like to find a formula that relates the distance from B to C with the initial velocity provided from A to B.
 ANSWER:
ANSWER:
Of course, you have to know the frictional force f and
the mass m of the car in general. Assuming that the force is constant
all along the path B to C, the distance s can be written s=�mv2/f.
In most cases f is proportional to m so that you do not
need to know the mass. If you are on level ground, f=μmg where
μ is called
the coefficient of friction and g=9.8 m/s2 is the
acceleration due to gravity (mg is the weight of the car). The
coefficient just is a parameter which is small if there is little friction.
So, finally you have s=v2/(2μg). If the car is on a
slope making an angle θ with the horizontal,
s=v2/(2μg∙cosθ).
 QUESTION:
QUESTION:
Okay I have wondered this question for many years, and more over have
wondered how to ask it! So I think a scenario is best; when an object is
propelled forward or in any direction very rapidly, let's say for this case
a bullet out of a gun, does it advance through every speed in between it's
current speed, zero, and it's maximum velocity or does it simply "jump" from
zero to it's maximum velocity? And also the same for when it hits its
target, let's say a thick steel plate does it go from its current velocity
straight to zero, or is there some sort of slowing down in which it goes
through every speed in between?
 ANSWER:
ANSWER:
Fundamental to classical physics is Newton's second law. That
which changes the speed v of something is a force F, a push or
a pull. Further, the bigger the rate of change of speed (acceleration a),
the bigger the force�double the force and you double the acceleration. This
is often written as F=ma where m is the mass of the object. Suppose
that you shoot a bullet from a gun. The bullet starts with a speed v=0
and ends with speed v and this happens in some time t and so
the acceleration can be written as a=v/t. If, as you suggest, the
bullet "jumps" instantaneously to v, then t=0. But for
t=0
the acceleration would be infinitely large which would imply that you had to
push on it with an infinite force. The same reasoning can be applied to
stopping the bullet. You know that the force propelling or stopping a bullet
in the real world is finite. It is a pretty good rule-of-thumb for everyday
occurances that there are no infinities or discontinuities (instantaneous
changes) in the universe.
 QUESTION:
QUESTION:
I am a member of US Coast Guard Forces. I am trying to describe to people
how hard it is to find them�so
wear a life-jacket so we have more time.
I am looking for an 'apparent size' formula, i.e., supposing someone's head is 1 ft high, what is its apparent size to me, on a boat 200 ft away, looking for that person (who hopefully still has his head above water!)
200 ft is ~ 1/10th of a nautical mile and is a standard separation distance for search and rescue patterns to run at.
 ANSWER:
ANSWER:
The way astronomers determine relative sizes of objects in
telescopes is the angle subtended by the image of the object. The angle, θ,
in radians, is given by θ=s/R where s
is the size of the object and R is the distance away. So if someone's
head is 200 ft away, it will be smaller by a factor of 20 than if it were 10
ft away. But you are actually looking at the area of the head, and that is
proportional to the square of its size, so that area would appear to be 400
times smaller than if it were 10 ft away. Another way to put it is that at
200 ft a 1 ft diameter head would look like a 12/20=0.6 inch ball at 10 ft,
maybe like a grape 10 ft away.
 QUESTION:
QUESTION:
Please help a work related dispute. Can the weight of a patient in a wheelchair be calculated using f=Ma? Even if it's a guesstimate?
I thought, if m= F/a
Where a = V2-V1 / t Where V2 is the velocity of the chair (and porter?) and V1 is coming to a stop.
Would F be the mass of the porter multiplied by the common acceleration of chair and porter?
I'm guessing if I clock the speed of the porter I can calculate a.
 ANSWER:
ANSWER:
I guess that "porter" means the guy pushing the chair. You have
it all wrong, I am afraid. But, it is worth talking about for a bit. There
are three masses involved here, Mpatient, Mchair,
and Mporter. There is an acceleration a which we
can agree could be roughly measured by measuring times and distances.
Suppose we first look at all three and call the sum of their masses M.
Then M=Fall/a where Fall is the
force which is causing the collective mass to stop. If you neglect the
friction which would eventually stop the wheelchair with no porter, Fall
is the frictional force between the porter's feet and the floor; you do not
know that force. Suppose you focus your attention on the patient. Mpatient=Fpatient/a
where Fpatient
is the force responsible for stopping the patient. This would be the
frictional force the seat of the chair exerts on the patient's butt; you do
not know that force. Suppose you focus your attention on the
porter. Mporter=Fporter/a where
Fporter is the force responsible for stopping the porter.
If we call the force with which the chair pulls on the porter Fc-p,
then Fporter=Fall-Fc-p;
you do not know either of these forces. I could go on and focus on the chair
alone next, but you can see that you do not know any of the forces which are
responsible for stopping any or all of the masses, so you cannot infer the
mass of any of them. Just knowing the acceleration, you cannot infer the
mass.
 QUESTION:
QUESTION:
Since radio waves are electromagnetic waves, do they attract Iron?
 ANSWER:
ANSWER:
The magnetic field in a typical radio wave is extremely weak
compared to a simple bar magnet and its effect on a piece of iron would be
very hard to observe. Also, since the fields are rapidly oscillating, the
average field over a period would be zero.
 QUESTION:
QUESTION:
I am writing a couple of SF novels that take place in significant part on a beanstalk station, i.e. a space elevator station located in geosynchronous orbit, and my question concerns the design. In my stories, the station is about a half mile wide with a shape similar to a hockey puck. The center third of the puck is attached to the elevator ribbon (both up to the counterweight and down to the planet of course) and fixed, therefore essentially in freefall.
My question concerns the outer section, which in my story spins in order to provide some g-force: is this a viable model? Some of my concerns are that the spin will create a gyroscopic effect as the station orbits around the Earth that will twist it off the ribbon or perhaps exert other forces on the hub that I'm not accounting for. One possible solution I thought of would be to split the outer section into two rings rotating in opposite directions to cancel out those effects.
Assuming some clever engineer works out the minor details of moving between the hub and the rotating section(s) is this design plausible? I like the science in my science fiction to be accurate and reasonable.
 ANSWER:
ANSWER:
I believe you are right to worry about the rotation causing
problems. If you just forget about the elevator and have a rotating "puck
station" in orbit, its axis will always point in the same direction in space
(conservation of angular momentum); so, if it were in a geosychronous orbit,
from earth it would appear to do a 3600 flip every day. I think that having a
counter-rotating ring would be a very good idea, the ring having the same
angular momentum (moment of inertia times angular velocity) as the main
station. If the station has a radius of about a quarter of a mile, about 400
m, the angular velocity ω needed to have an earth-like artificial
gravity (g=9.8 m/s2) at the edge would be
ω=√(g/R)=0.16
radians/s=0.025 revolutions/s≈1.5 rpm.
 QUESTION:
QUESTION:
In the Meissner effect; when the falling bar magnet's descent is arrested due to the magnetic impermeability of the supercooled lead dish toward which it is falling, what happens to its inertia? Does the field around the bar magnet deform and absorb it, or does something else occur?
 ANSWER:
ANSWER:
It is essentially the same as if the magnet were attached to an
unstretched spring (no superconductor) and dropped; as the magnet falls, gravitational
potential energy decreases and spring potential energy increases but faster. The magnet
will speed up until eventually you reach a point (equilibrium point) where
the force from the spring (up) is the same as the weight of the magnet (down)
and then it slows down, eventually going back up and so on. Because there are
drag forces (air drag and the damping in the spring) it settles down to the
equilibrium point. In the Meissner effect, the magnetic field of the magnet plays
the role of the spring in my simple analogy. Because the superconductor
excludes the field, the field deforms as the magnet falls and pushes back up
harder on the magnet as it gets closer to the superconductor which means
that the energy of the field is increasing. You were essentially right in
your speculation that "�the
field around the bar magnet deform[s] and absorb[s]�"
the kinetic energy.

 QUESTION:
QUESTION:
Regarding a atomic blast. What are what appears to be thin streamers on the outside of the mushroom cloud? They are some distance away from the cloud and go from the ground to the cloud itself.
 ANSWER:
ANSWER:
I assume you mean like shown to the left. These are the
contrails of rockets shot off just before the blast; their purpose is to
detect the shock wave from the explosion.
 QUESTION:
QUESTION:
Is it true that even an electron has its north and south poles; if it
is, then how?
 ANSWER:
ANSWER:
A simple bar magnet (shown blue) has a magnetic field shaped as
shown by the right-most figure to the right. What is fundamental is the
shape of the field, not the N and S poles of the bar. This is called a
magnetic dipole field. To the left of this is the magnetic field caused by a
current loop. Notice that this little current loop has a very similar field
shape, so you could identify its N and S poles. An electron has an angular
momentum, that is it is spinning. A spinning ball of electric charge is like
a stack of tiny current loops, so it will also have a dipole-shaped field.
Therefore you could say that an electron has a north and south pole.
 QUESTION:
QUESTION:
What makes neutron radiation so dangerous?
 ANSWER:
ANSWER:
Mainly, it is because they can cause an atomic nucleus to become
radioactive. If a neutron is absorbed by a nucleus of an atom in your body,
it will most likely become a radioactive nucleus which will decay and the
decay products (beta or gamma rays) will be ionizing radiation which will do
damage to the molecules in your body.
 QUESTION:
QUESTION:
Hypothetically, what
would be the energy (in joules) required to maintain a specific car
(described below) at 50 mph on a flat concrete surface for 1 mile. No, it's not homework. I'm a 20 year old college dropout. It's a design I started in college and wanted to finish. The
specifics of the car are as follows:
-
Total weight: 205 lbs
-
rolling
resistance: μ=0.0025
-
drag coefficient:
cd=0.14
-
Frontal Surface area:
A=13.295 ft2
 ANSWER:
ANSWER:
First you need to find the rolling friction which is easy
because on level ground the force is the coefficient of friction times the
weight: Fr=0.0025x205=0.51 lb. The drag friction is a bit
harder because it depends on the speed v=50 mph=73.3 ft/s and
the mass density of the air, ρ≈0.002377
slugs/ft3 (I hate working in English units!):
Fd=�ρv2cdA=�x0.002377x73.32x0.14x13.295=11.89
lb. So the net force is 12.40 lb which is, of course, the force you must
exert over the distance of a mile; therefore the energy required is the work
done which is W=12.40x5280 ft∙lb=65,449
ft∙lb=88,737
J. Just
to check that this is reasonable, you could calculate the power, energy per
unit time. The time to go one mile is about 72 s and so the power delivered
to the car is about
88,737/72 J/s=1232
W=1.65 hp. That seems on the low side to me, but that is how it comes out
with your numbers.
To double check, I redid the calculation in SI
units: First you need to find the rolling friction which is easy
because on level ground the force is the coefficient of friction times the
weight: Fr=0.0025x93x9.8=2.28 N. The drag friction is a bit
harder because it depends on the speed v=50 mph=22.4 m/s and
the mass density of the air, ρ≈1.225
kg/m3:
Fd=�ρv2cdA=�x1.225x22.42x0.14x1.235=53.14
N. So the net force is 55.42 N which is, of course, the force you must
exert over the distance of a mile; therefore the energy required is the work
done which is W=55.42x1609 J=89,171
J. Just
to check that this is reasonable, you could calculate the power, energy per
unit time. The time to go one mile is about 72 s and so the power delivered
to the car is about 89,171/72 J/s=1238
W=1.66 hp which is about the same answer as above.
 QUESTION:
QUESTION:
Hello, we are having a debate over which syringe and needle are less painful for injections. Assuming the exact same amount and viscosity of the material (whether normal saline or a viscous medication), if a 3cc syringe is attached to the same 30gauge needle as a 1cc syringe, which is less painful to receive the injection? The 3cc syringe is appx the same length of the 1cc syringe, with a wider barrel.
Some feel with Poisoille law, the velocity of med pushed is slower with a 1cc syringe, so the med injected slower in 1cc is less painful than a 3cc.
Some feel the 3cc is less painful because the pressure of pushing is dispersed over a larger diameter, so less pressure is less pain.
Others feel, that even though the 3cc is wider than 1cc syringe, all is neutralized because the 30g needle attached is the same.
We are assuming the pain of the injection is related to the push of the medication, but cant decide if velocity of flow or pressure of push is the main factor. We know if med is pushed quickly, it is more painful. But we can't quantify the difference between 1cc and 3cc syringes, other than anecdotes... Can you help with a physics explanation?
 ANSWER:
ANSWER:
I am not a physician, so I cannot speak to the question of pain.
I have considered a
very
similar question before and concluded that
Poiseuille's law is irrelevant here. The only difference between the two is
that the 3 cc syringe, having a larger barrel than the 1 cc syringe, will
result in a smaller pressure pushing out the medication if both are pushed
with the same force; with identical needles, therefore, the 1 cc syringe
will result is a faster fluid flow. So, if you know that faster is more
painful, the 3 cc syringe should be used.
 QUESTION:
QUESTION:
Let's say you're playing baseball and your standing in the field by a base and someone threw the ball to you so that you could get the person running to the base you're by out. So you look and you see the ball coming towards you.
Is it possible that while you're starring, concentrating on the ball that time or at least the ball looks like its slowing down and if so is it just your brain playing tricks on you?
 ANSWER:
ANSWER:
In fact, the ball is
slowing down the whole time it is coming toward you because of air drag.
However, I do not believe that you would be able to tell that. What is
certainly true is that time does not slow down as you wait for the ball to
arrive. I suppose that it is possible that your concentration on catching
the ball results in it looking like the ball is slowing down, but that is
not really physics.
 QUESTION:
QUESTION:
hi, me and my friend are having a debate on wind turbines or anything that travels in a circular motion. one of us say that the very tip of the turbine blade is traveling faster than the inner part that is close to the axis. we both agree that it has the same rpm but what part travels at a faster mph?
 ANSWER:
ANSWER:
The velocity is proportional to the radius of rotation, so a
point twice as far from the axis as some other point is traveling twice as
fast.

 QUESTION:
QUESTION:
I need a very brief explanation for Kindergarteners. (I just
want to use the right words; they can learn the details of what they mean
later.) In an amusement park ride in which long swings are spun around a
central pole, why do the swings rise up as the pole spins faster? (I assume
it's the same reason that a skirt rises up when the person wearing it
twirls.) Is it something to do with centrifugal force? Centripetal force?
Nothing I saw on the web about these forces seems to explain why the objects
rise, only why they move to the inside or outside of the orbit.
 ANSWER:
ANSWER:
For Kindergarteners, use of centrifugal force is probably best.
I guess the merry-go-rounds we had on playgrounds when I was a kid have been
deemed unsafe, but get your students to appreciate that the faster they are
spun on something akin to this, the harder it is to hang on. This is because
the centrifugal force which tries to push them off gets bigger as the
merry-go-round spins faster. Then you can just take a pendulum and
demonstrate that the harder you pull, the higher it rises. The little
diagram to the right shows the effect of the the centrifugal force F which will lift the pendulum bob higher as
it pulls harder.
 QUESTION:
QUESTION:
I have a question that been thats been unanswered from quite some time now. I even tried asking that to a person in NASA houston and he couldn't even understand. Hope you can help.
We know that space dust and debris keep on falling on earth. And I have read that its many tons a day. Considering mass of earth is increasing every day for millions of years now, how does it affect its revolution, speed and axis. Or does it even affect that.
 ANSWER:
ANSWER:
One estimate is that the earth gains 40,000 metric tons (4x107
kg) per year. So, in a million years that would be a gain of 4x1013
kg. The mass of the earth is 6x1024 kg. The moment of inertia
will be proportional to the mass times the square of the radius, so,
assuming the change in radius is negligible, the fractional change in moment
of inertia over a million years would be approximately 4x1013/6x1024≈10-9=10-7
%. Since angular momentum (moment of inertia times angular velocity) is
conserved, this would mean that the angular velocity would decrease by about
10-7 %, an increase in the length of a day of about (24 hr)(3600
s/hr)x10-9≈10-3
seconds in a million years!
 QUESTION:
QUESTION:
At the LHC protons travel at .999999991 c, or about 3 metres per second slower than the speed of light. I the the proton is also spinning at above 3 metres per second in the direction of travel wouldnt at least part of the proton for a brief period of time exceed the speed of light.
I'm guessing the answer is no because all answers involving exceeding the speed of light are no, but i'm having trouble understanding why.
 ANSWER:
ANSWER:
Many elementary particles, for example the proton in your
question, have "spin" which is intrinsic angular momentum. However, you are
attempting to model this angular momentum classically, that is by thinking
of the proton as a little spinning ball. However, a proton is not a
classical object and it is incorrect to model it as such. Any attempt to
classically find the speed of the "surface" using reasonable numbers for the
radius and mass distribution will result in nonsensical results.
 QUESTION:
QUESTION:
While looking towards the northwest after dusk on 7-31-14 in Honolulu, we noticed the quarter moon about 45 degrees above ground level. About an hour and a half later, the moon appeared to be about 15 degrees above ground level. Finally, about another half hour later, the moon was no longer visible. I have never seen the moon move so quickly and I'm wondering whether there is a scientific explanation for this?
 ANSWER:
ANSWER:
I looked up the
moonrise and
moonset times in Honolulu on this date: 10:02 AM and 10:12 PM. So the
time across the sky is about 12 hours. The time it takes to travel 450
would be about (45/180)x12=3 hours. Your times and angles are approximated,
so your approximated time, 2 hours, is not surprising. Also, if there was
anything abscuring the horizon�trees buildings, clouds�the time would have
been shortened.
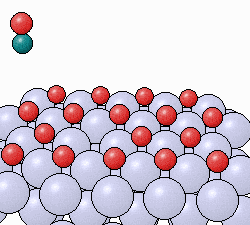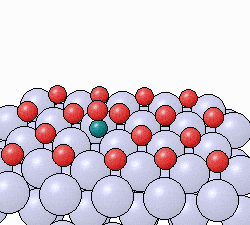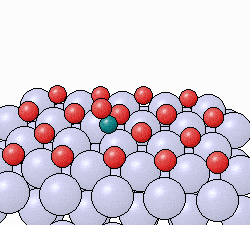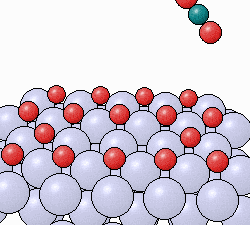
 QUESTION:
QUESTION:
What is the meaning of the moving diagram at the top of your home page? the blue and red balls...
 ANSWER:
ANSWER:
It supposedly represents a catalytic converter where carbon
monoxide, CO hits the metallic crystal into which oxygen has been adsorbed,
picks up an oxygen atom, and departs as carbon dioxide, CO2.
 QUESTION:
QUESTION:
If I'm not mistaken helium 3 is a very powerful energy source. But there is very little of it on earth.
There is lots of it on the moon. so what problems would we run into if we extracted it from the moon why haven't we already done it?
 ANSWER:
ANSWER:
3He is a potential fuel for a nuclear fusion
reactor. The energy producing reaction is 3He+2H �>
4He+1H+energy; here
2H is heavy hydrogen or deteurium
(proton plus neutron plus electron) and 1H is normal hydrogen
(proton plus electron). There isn't necessarily more
3He on the moon, it is just thought
to be more abundant relative to the much more abundant 4He there.
The interesting thing about helium is that it does not form molecules
because it is inert; and, because it is so light, if it appears in the
atmosphere it moves so fast that it escapes right into space. The best
source of helium on earth is to separate it from natural gas with which it
has been trapped underground. The reason that we have not already gotten it
from the moon is that it is terribly expensive to send spacecraft to the
moon and we would also have to develop the technology to extract it from the
moon rocks in which it is embedded and transport it back to earth. Even if
that were not a problem, the simple fact is that, in spite of decades of
trying, we have been unable to build a nuclear fusion reactor which can
produce more energy than it consumes and we are still decades away from
having a commercial fusion reactor. There is a kind of funny saying about
nuclear fusion: "Nuclear fusion is the energy of the future and always will
be!"
 QUESTION:
QUESTION:
I was explaining conservation of energy to my daughter when she was spinning on our office chair, and her rotational velocity increased as her moment of inertia decreased when she pulled her arms and legs toward the rotational axis. Is there an analogous example for linear motion, where the linear velocity increases as the mass decreases? I can't think of a real-world example of a body whose mass decreases (or increases).
 ANSWER:
ANSWER:
Actually, you were demonstrating conservation of angular
momentum, the product of the angular velocity and moment of inertia remains
constant for an isolated system. Energy is not conserved because rotational
energy is proportional to the product of the square of
the angular velocity and moment of inertia.
But, you explained it correctly for your example. So, your question is if it
is possible for conservation linear momentum, the product of mass times
velocity, to result in a changed velocity due to a change of mass. You do
not usually see as many examples of this as for angular momentum because
rotating things change shape frequently whereas moving objects usually do
not have significant change of mass. The classic example is a conveyer belt
onto which mass is being dropped from a hopper. If you had a very long
frictionless conveyer belt with mass on it, it would have a certain linear
momentum. Now, if you start dropping mass on it, it will slow down.
Similarly, if you let mass drop off the end of the conveyer belt without
replacing it, it will speed up.
 QUESTION:
QUESTION:
Some time ago I found a quantum lecture series on the web. I thought that even if I didn't "get" all the math, I would still perhaps learn something. Well, the lectures were "here is some math you will need for quantum mechanics," "here is some more math you will need, etc." I skipped ahead many lectures and found the next lecture was "here is some MORE math you need, etc."
I am wondering this: Is quantum mechanics something like the Ptolemaic system where the math works even though there is no REAL understanding of the underlying phenomena?
 ANSWER:
ANSWER:
No question�quantum mechanics is quite mathematical as are most
advanced topics in physics. It's the nature of the beast, I guess. But it
should be possible to convey the essence of just about any topic in physics
with minimal mathematics or even none. That, after all, is what I aim for at
AskThePhysicsit.com. So, is quantum mechanics comparable as a theory to the
Ptolemaic description of the solar system? I would say certainly not. So,
originally Ptolemy postulated circular orbits for the planets and satellites
which did a fairly adequate job for the 2nd century. But then there were
more observations which were not described and one had to add epicycles to
the Ptolemaic system, sort of circles on circles. It all became contrived to
just fit the data and eventually was given up as a failed idea. Quantum
mechanics, on the other hand, matured rather quickly from its sketchy
origins (black body radiation, photoelectric effect, Bohr model, Compton
scattering) to what today is called nonrelativistic quantum mechanics. If
applied to experimental results over a time period of about 80 years, the
theory has never failed to be correct. But just because it works wonderfully
well does not mean we really understand it. I think most physicists would
agree that we do not have an answer as to "why it works" or whether there is
an underlying possibly more deterministic physics. Certainly Einstein was
never comfortable with quantum mechanics. To compare it to the purely
empirical Ptolemaic "theory" really sells it short.
 QUESTION:
QUESTION:
This might seem dumb, but i cannot understand the laws of thermodynamics applied to gravity.
If a moon orbits a planet in a stable orbit, it still pulls on the planet, and the planet pulls on the moon. This seems to generate heat (the heatsource on europa) and motion (tidalwaves on earth). How can this not violate the laws of thermodynamics?
 ANSWER:
ANSWER:
The first law of thermodynamics, which seems to be the crux of
your question, is nothing more than conservation of energy. Energy
conservation is true only for isolated systems, so let us think about a
single planet and a single moon isolated from everything else. In addition
to the simple central force of gravity, the two interact with each other via
tidal forces which result
from the sizes and relative masses of the two. Just what the effects of the
tidal forces are depends a lot on the relative sizes and distances of the
two, but, as you note, often appear to violate energy conservation. So,
let's look at that more closely. Soon after the moon was created, probably
by a cataclysmic collision with an asteroid, it was much closer to the earth
than today and it rotated on its axis at a much faster rate than it does
today (about 28 days, which is why it always shows the same side to us). The
tidal force caused what is called "tidal locking", the same side always
facing the earth. It would seem that this would represent a loss of energy
since it is not spinning as fast as it used to be, but as this happened, the
moon moved farther and farther away from the earth which represents an
increase in energy. So, the energy of the whole system stayed the same.
Today, the tidal effect is mainly due to the ocean tides on the earth and
now it is the earth which slows down its rotation�the earth is losing
rotational kinetic energy and tending toward being tidally locked with the
moon. This is an extremely small effect�a day gets about 2 milliseconds
shorter during one century. But, just as was the case when the moon was
slowing down its rotation, the way energy is being conserved is by the moon
moving farther away, resulting in an increase in the earth-moon energy
keeping the total energy constant. If the tidal forces are great enough to
cause significant frictional heating because of the tidal force distortion
of the whole moon (your Europa example), energy is lost because some of the
heat is radiated into space. So the first law would be violated, but you
would expect that since some energy is escaping from the planet-moon system.
You can see that your error was to assume a "stable orbit".
 QUESTION:
QUESTION:
How long does it take to stop a 7000 lbs vehicle at 45 mph? Time and distance please.
 ANSWER:
ANSWER:
You have not given me enough information, in particular what are
the wheels and the surface made of; surely you realize that a truck stopping
on ice will go much farther than a truck stopping on a dry road. I will work
it in general and then calculate it for a typical example. The quickest stop
you can affect is to apply the brakes hard enough that the wheels are just
about to start skidding; that is what anti-skid braking systems do.
Therefore the force F which is stopping you (on a level road) is the static
friction between the road and the wheels, F=μsW
where μs is the coefficient
of static friction between the wheels and the road, W=Mg is the
weight of the vehicle, M is the mass, and g=32 ft/s2
is the acceleration due to gravity. But, Newton's second law tells us that
also F=Ma where a is the acceleration of the vehicle.
Therefore, the acceleration is independent of the mass of the vehicle and
the acceleration is a=μsg.
Now that you have the acceleration you can write the equations of motion
for position x and velocity v as functions of time t:
x=v0t-�at2 and v=v0-at
where v0=45 mph=66 ft/s. Now, you need to specify
what
μs is. For example, μs≈0.9 for rubber on
dry asphalt, so a≈0.9x32=28.8 ft/s2 and I find t≈66/28.8=2.3
s and x=66x2.3-�x28.8x2.32≈76 ft.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I'm trying to figure out if a traffic light at an intersection is timed too short for a heavier vehicle to stop in time. The speed limit is 45mph, the vehicle weighs ~7000 lbs (7200 empty w/driver) , there is a downward slope of which I'm trying to find out. Yes to dry pavement. What would you need to figure surface area of rubber/tire? And I need to time the light still. With all of the above information would you be able to calculate that?
 ANSWER:
ANSWER:
As I showed above, the weight is irrelevant. Of course, this is
an approximation as all friction calculations are, but a quite good one for
this situation. It is also important that my calculation is the shortest
time and minimum distance, what you would get by flooring the brake pedal
with anti-skid braking operating. If you do not have anti-skid braking and
you lock your wheels, it will take longer and go farther. Also, there is the
possibility that μs
could be different from 0.9 depending on local conditions (temperature,
surface condition, etc.). It is important to include the slope in the
calculation. If the slope is down as you say, the acceleration (I am
assuming you are not interested in the details) is a=32(μscosθ-sinθ)
where θ is the angle of the
slope; for example, if θ=200
and μs=0.9, a=32(0.9x0.94-0.34)=16.2 ft/s2,
quite a bit smaller than the value of 28.8 ft/s2
for a level road. Once you calculate the
acceleration, the expressions you can use for time and distance are t=66/a
and x=2178/a, respectively. So, for a 200 slope,
t=4.1 s and x=134 ft. Again, this is the lower limit. I think an
engineer would build in a factor of 2 safety factor. You do not need to know
what the surface area of the contact between the rubber and the road is.
 QUESTION::
QUESTION::
Nothing can accelerate itself by applying force on itself. Besides, isolated forces do not exist and they exist in an action reaction pair.
These are the essence of Newton's third law. When an engine exerts force on a bike how can it accelerate the bike taking bike as a system in this argument? After all, a part is exerting force on another part , right?
 ANSWER:
ANSWER:
The engine exerts a torque on a wheel trying to make it spin. If
the bike were on ice, the wheel would spin, there would be no acceleration
and therefore there must have been zero net force on the bike+engine as you
surmise. However, if there is friction between the wheel and the ground, the
ground exerts a force on the wheel which is forward; this is the force which
drives the bike forward. Note that the wheel exerts a force backward on the
ground (Newton's third law) but the ground does not move because it is, effectively, infinitely
massive.
 QUESTION:
QUESTION:
There is a debate at my office regarding this question
If you are on a bus traveling at 20 mph and you run from one end of the bus
to the other at 5 mph, how fast are you going? Can you answer and explain?
 ANSWER:
ANSWER:
I must have answered similar questions a hundred times! Whenever
you ask about what a velocity is, you must specify velocity with respect
to what. I am assuming you mean velocity relative to the ground. If the
bus is going forward and you are running toward the back, your velocity is
15 mph in the same direction the bus is moving; if you are running toward
the front, your velocity is 25 mph in the same direction the bus is moving.
 QUESTION:
QUESTION:
A while back my friend and I were playing computer games my room together. We noticed that it was getting very hot in the room and I said "just think how hot it would be if we didn't have efficient CPU coolers!" He responded, "It would actually be cooler in here if we didn't have efficient coolers because more heat would be in the CPU and less would be in the room."
My question is this, would the overall heat in a room occupied by gaming computers be higher with less efficient CPU coolers or would it be higher with more efficient CPU coolers?
 ANSWER:
ANSWER:
The CPU generates a certain amouint of power in the form of
heat. You want to get that away from the CPU so you install some kind of
cooler. The simplest would be just fins thermally coupled to the chip to
radiate the heat away faster due to increased effective surface area. In the
long run, either of these will end up heating the environment at the same
rate because both are generating the same power, it is just that the
equilibrium temperature of the chip or chip+radiator will be different. The
next simplest cooler would be a fan; but a fan itself consumes power and so
it adds to the total power dumped into the room. This would come from the
heating of the fan motor. Or, you could have some kind of refrigerator;
again, this would add more heat to the room than the power generated by the
CPU. A refrigerator extracts heat from one place and dumps heat in another.
Because of thermodynamics, the heat dumped is always greater than the heat
extracted. For example, you should not cool your kitchen by opening the door
of your refrigerator because the coils at the back put more heat into the
room than the cooler takes out. Finally, if you have some kind of liquid
cooling and dump its heat somewhere outside the room, the overall effect
would be to heat the room less.
 QUESTION:
QUESTION:
Does the centrifugal force really exist?
 ANSWER:
ANSWER:
I guess that depends on what you mean by "exist". In the sense
that it is a real force, the answer is no. Newton's laws are not valid if
you are accelerating. For example, read an
earlier answer on an why
you fall over in a bus which is suddenly stopping; this answer will also
lead to links on centrifugal force for a
bicycle
and a car. It turns out that you can make Newton's laws to be valid in
accelerating systems if you introduce "fictitious forces" and centrifugal
forces are fictitious.

 QUESTION:
QUESTION:
I'm a non-scientist researching the issue of the relative efficiency of water transportation versus land and air transportation. The studies I consult all indicate that bulk cargo transportation by water is far more efficient than land or air transportation, but they stop short of getting into the physics of why this is so. Something to do with friction, I imagine--but exactly what?
 ANSWER:
ANSWER:
I am sure there are lots of considerations. Since you mention
friction, let's run with that. I will compare ground with water
transportation. Imagine a truck or a train, completely empty. For it to
drive at a constant speed the engine must provide a certain power, energy
delivered per unit time; the reason that it cannot just move forward without
an engine is that there is friction of various kinds�in the axels, in the
rolling of the wheels, and air drag. The drag depends only on your speed, so
if we agree to go a certain speed, this friction can be ignored. The rest of
the friction is determined by the weight of the train or truck. Now, suppose
you load the train or truck with cargo, say 10 times the weight of the empty
train or truck. Friction (other than drag) will increase by a factor of 11
because friction is proportional to the total weight. So you need almost 11
times more power to maintain the constant speed. Now think about a ship. All
the friction is drag, air drag and water drag. These now depend on speed but
there is no friction which depends (directly) on the weight. If you add 10
times the weight as we did before, the ship will go down deeper in the
water; this will increase the water drag somewhat, but it will certainly not
be 10 times bigger as was the case for ground transport. Roughly speaking,
the drag will be proportional to the cross sectional area of the ship in the
water and I would be surprised if that doubled when loading a ship.
 QUESTION:
QUESTION:
My question pertains to sound and how it manages to traverse all sorts of mediums - gas, liquid, solids. Specifically, it is simply amazing to me how well it propagates and we can pick it up with our ears, given that the original source of the sound often has a relatively low energy source. For example: I am lying in my bed at home, have the covers over my ears, my windows are closed, the blinds are down and I can still hear people talk outside on the sidewalk, even though the trajectory of the source (vocal cords, mouth cavity of the speakers) is not linear to my window and bed and ear under the covers.
How can the rather minute energy that vocal chords produce manage to traverse such increadible obstacles by making atoms and molecules vibrate in all these different mediums? I just dont get it...
 ANSWER:
ANSWER:
You are certainly right that sound carries very little energy.
We should note that, were it not for the resonant properties of the head,
chest, and mouth, the sound made by vibrating vocal chords would be much
smaller yet. There are essentially two answers to your question: it takes
very little energy to get a molecule vibrating and the ear is a remarkably
sensitive sound detector.
 QUESTION:
QUESTION:
Why don't electrons fall into the nucleus?
 ANSWER:
ANSWER:
Why don't the planets fall into the sun? Because they are in
orbits and the gravity from the sun bends the paths of the planets as it
pulls on them and the result is an orbit rather than a fall. Really, a
straight fall is just a special kind of orbit; or, put another way, an orbit
is a constant free fall. So, think of electrons as like planets and the
nucleus as like the sun and the force is electrical rather than
gravitational. But there is something different about electric charges. As
you can see from the answer two questions below this one, an accelerating
charge radiates electromagnetic radiation; so the question is why the
electron, which is accelerating in its orbit, does not radiate its energy
away and spiral into the nucleus. This is because in quantum mechanics we
find that the electron can only exist in certain orbits and a "free fall
orbit" is not one of them.
 QUESTION:
QUESTION:
I am standing in a field. 200 m away someone fires a gun and at the same time in the opposite direction 200 m away someone screams. Would I hear the gun first, scream first, or both at the same time?
 ANSWER:
ANSWER:
If there is no wind, the sounds would reach you simultaneously. The velocity of sound is independent of the loudness. The speed of sound is about 340 m/s so you would hear each sound 200/340=0.59 s after it was emitted. The reason I stipulate no wind is that the sound travels with respect to the air, not the ground. So, if the wind speed were 100 m/s (over 200 mph, so not likely!) toward you from the direction the train was coming, you would
observe the sound from the train approach you with speed 440 m/s and from the girl 240 m/s. You would hear the train at a time 200/440=0.45 s and the girl at a time 200/240=0.83 s.
 QUESTION:
QUESTION:
How are radio waves created within antennas?
 ANSWER:
ANSWER:
The way you make radio waves is to accelerate electric charges.
So, about the simplest antenna you could make would be a conducting rod.
Apply a sinusoidally varying potential difference of frequency
f, V=V0sin(2πft),
across the ends of this rod and it will cause the electrons to oscillate
with the same frequency such that their positions are of the form x=Asin(2πft),
so their accelerations are a=d2x/dt2=-4π2f2Asin(2πft).
The result will be electromagnetic waves with frequency f.
 QUESTION:
QUESTION:
Say I have a syringe fully compressed, then seal the spout end. Now I pull out the plunger creating a vacuum inside. Will the force required to pull the plunger back be the same throughout the length of the pull?
 ANSWER:
ANSWER:
The force required to hold the plunger at any place is the
product of its area times the atmospheric pressure, provided there are no
air leaks. This is independent of how far along the length of the syringe
you are.
 QUESTION:
QUESTION:
I looked up how our astronauts breathe on the ISS; splitting water molecules into gaseous hydrogen and oxygen (H2 and O2). So my question is: how much water would natural processes have to had split for there to be as much oxygen that is present in our current atmosphere?
I assume that's a tough one to answer without engineers etc. I just wish there was already an answer available.
 ANSWER:
ANSWER:
This is not particularly "tough" to estimate. The total mass of
the atmosphere is about 5x1018 kg and about 1/5 of that is
oxygen; so there is about 1018 kg of oxygen in the atmosphere.
About 90% of the mass of water is oxygen, so the total amount of water you
would have to split would be about 0.9x1018 kg. I believe that
the origin of our atmospheric oxygen is from plants (cyanobacteria, to be
precise), though, where photosynthesis turns carbon dioxide and water into carbohydrates and oxygen.
 QUESTION:
QUESTION:
Is there a difference between a proton and photon, besides their difference in charge?
 ANSWER:
ANSWER:
It is hard to imagine two more different particles:
-
protons are fermions (spin
�), photons are bosons (spin 1)
-
protons have mass, photons no
not
-
protons are composite
particles (quarks and gluons), photons are not
-
photons are the quanta of the
electromagnetic field, protons are baryons
-
protons have electric charge,
photons do not
-
photons have an "h", protons
have an "r"
 QUESTION:
QUESTION:
Isn't the fact that Andromeda galaxy (being the galaxy supposedly going through a
collision with the Milky way in millions of years) defying the dynamics of
dark energy? Shouldn't it be moving AWAY?
 ANSWER:
ANSWER:
The expansion of the universe is the behavior on average, not
some kind of absolute rule. Imagine that you drop a stone�shouldn't it move
away from the earth? Local gravitational fields and initial conditions often
trump the overall expansion properties. The Andromeda and Milky Way galaxies
are attracted to each other gravitationally and since they never have had a
large velocity moving away from each other, they are doomed to fall into
each other.
 QUESTION:
QUESTION:
In the topic of radiation therapy, they say that the photoelectric effect is used.
It is said that in radiation therapy "an incoming photon collides with a tightly bound electron." However where does this electron come from?
 ANSWER:
ANSWER:
Every atom in the material through which the photon is traveling
has electrons. They are not added, they are already there.
 QUESTION:
QUESTION:
When a bullet hits a door and gets embeded in it, no external force acts on the system of door and bullet but why is linear momentum not conserved and the angular momentum conserved? Can you give some examples where angular momentum is conserved but not linear? Can it be possible to have both linear and angular momentum conserved?
 ANSWER:
ANSWER:
I presume you are alluding to the classic introductory physics
problem of a bullet hitting a door mounted on frictionless hinges. Angular
momentum is conserved if there are no external torques, and since hinges
cannot exert a torque, it is. Linear momentum is conserved if there are no
external forces but the hinges exert a force on the door during the
collision time and so it is not. If the hinges were not there, the door and
the bullet would move forward and rotate about their center of mass
conserving both linear and angular momentum.
 QUESTION:
QUESTION:
What is the change in velocity of the earth's rotation if a person (myself) who weighs 60 kg were to stand on something about a foot tall.
Ps this is not a homework question, I'm just a curious teen who's never taken physics. Also it's the middle of the summer for me in
New Orleans.
 ANSWER:
ANSWER:
The glib answer to this question would be, for all intents and
purposes, the change in rotation would be zero. It is a good opportunity
to talk about the physics involved and to estimate how small small is here. The moment of inertia of the earth is about
Ie=8x1037
kg∙m2. Your moment of inertia if you are on the earth's
surface is about Iy=60x(6.4x106)2=2.5x1015
kg∙m2. The moment of the
earth plus you is I=Ie+Iy≈Ie=8x1037.
If you increase your distance by the amount 0.3 m, about 1 ft, your moment
of inertia increases to Iy+ΔI=60x(6.4x106+0.3)2=Iy(1+4.7x10-8)2≈2.5x1015(1+2x4.7x10-8)=2.5x1015+ΔI
and so ΔI=9.4x10-8
kg∙m2. So you and the earth
start with I=8x1037
and end with I+ΔI=8x1037+9.4x10-8.
The operative physical principle here is conservation of angular
momentum, the product of moment of inertia and angular frequency ω=2π/T
where T is the period, 24 hours: Iω=(I+ΔI)(ω+Δω)=Iω+IΔω+ΔIω+ΔIΔω.
Neglecting ΔIΔω, Δω/ω=-ΔI/I=-1.2x10-45;
note that since Δω/ω<0, the frequency decreases, the rotation
slows down. Now, it is pretty easy to show that ΔT/T≈-Δω/ω=1.2x10-45
or the day gets longer by 24x1.2x10-45=2.8x10-44
hours! Your contribution to the earth's moment of inertia is so tiny that
anything you do to change your own moment of inertia will have no measurable
effect on the rotation of the earth.
 QUESTION:
QUESTION:
I know that a subatomic particle can be in two places at once so if you took these particles and set them side by side ( before they managed to disappear) would they have the same mass as just one or one squared or one times two?
 ANSWER:
ANSWER:
In quantum mechanics we do not talk about the position of
a particle, we talk about the probability of finding the particle at some
position. Thus, there might be two places where the probability of finding a
particle is the same, and that is where the popular notion of a particle
being "in two places at once" comes from. However, once you do a measurement
which locates the particle, it is all there and somewhere else where it
might have been before you observed it no longer has any probability of the
particle being there. The measurement is sometimes referred to as collapsing
the wave function.
 QUESTION:
QUESTION:
If I lift a book for thirty minutes I feel tired. Physics says that
I did no work but it also says that if energy is lost some amount of work has to be done (though it may result in net zero work). Why do we feel tired without performing "work in the language of physics"
 ANSWER:
ANSWER:
In the example of simply holding up a weight in an outstretched hand,
physics would say no work is being done because the force on the weight is not acting over a distance; you and I both know, however, that sugar is being burned to provide the energy necessary to hold this weight stationary. What is going on there, as I understand it, is that the muscle fibers in your arm are continually slipping and retensioning thereby doing lots of little parcels of work to hold your arm steady.
 QUESTION:
QUESTION:
My friend believes there is the energy potential in a small rock to run a city for days. Is this theory correct?
 ANSWER:
ANSWER:
If you could find a way to change all the mass of that stone into energy you could get an amazing amount of energy. For example, suppose the mass were 100 grams=0.1 kg. Then the energy there is
mc2=0.1x(3x108)2 which is about 1016 J. Suppose you spread this out for a week; then the power would be
(1016 Joules)/[7 day(24 hour/day)(3600 second/hour)]=16.5x109
Watts=16.5 GW. This is about twice a large as the largest nuclear power plant in the world.
Unfortunately, the most efficient way to generate large amounts of power
(nuclear fusion, the energy of the sun and the hydrogen bomb) is only 1%
efficient.
 QUESTION::
QUESTION::
If two magnets are in zero gravity would one magnet repel faster than the other or would they equal the same force?
Also if u connect somehow an electromagnet and normal magnet in zero gravity when electoral is turned on would the magnet wit the greater force be able to pull/push the other magnet with it if they connected?
What speed would magnet repel magnet at zero gravity?
Thank you.
If u could control the amount f magnetism would there b a limit on speed at zero gravity?
 ANSWER:
ANSWER:
You have several misconceptions here. First of all, the
fundamental physics is independent of whether you are in zero gravity or
not. Just to keep things simple, let's say there is no gravity. If you have
two magnet aligned such that like poles are facing each other, repulsion
will result as you suggest. The first thing you need to understand is that,
even if one is very strong and one is very weak, the force that one exerts
on the other is exactly the same as the other exerts on the one; this is
Newton's third law. Now, just because you know the force, you cannot
automatically find the velocity of either magnet, you need more information;
for more information on this, see my FAQ
page. What will happen is that the forces (F) will cause each magnet
to have an acceleration (a) away from the other, but the more mass (m)
the magnet has, the smaller the acceleration will be, a=F/m;
this is Newton's second law. It is complicated to calculate how much speed
each would acquire, impossible if you do not quantify the strengths and the
distance apart. The simplest case would be a very light magnet near a very
heavy magnet; if you knew the amount of energy it took the bring the light
magnet in from very far away, call it W, the the speed v it
would have long after you let it go could be calculated from the equation W=�mv2 or
v=√(2W/m)
 QUESTION:
QUESTION:
Is the energy needed to increase the temperature by 5 degrees, for example, the same energy needed to decrease the temperature of the same matter by 5 degrees?
 ANSWER:
ANSWER:
I think you mean "the same energy
released to decrease the temperature"; you do not add energy to decrease temperature.
The answer to your question is that it depends on how you heat and cool. An
example of where it would not be the same is if you heat a gas allowing it
to expand at a constant pressure and then cool it keeping its volume
constant, the energy you put in would be more than the energy you got out.
 QUESTION:
QUESTION:
My question is, (I was wondering about this yesterday,) suppose you have a doughnut shaped metal pipe. Within that metal pipe you placed a sphere shaped magnet, being just big enough so as to not touch the inside walls of the pipe. Now inside the doughnut shaped pipe is vacuum, at the same time since the force of gravity is there. What would the velocity be of the sphere shaped magnet inside? Would it increase, decrease gradually with time or stay constant?
 ANSWER:
ANSWER:
This is just a variation of the
classic problem of dropping
a magnet down a conducting pipe. If you put inside at rest it will stay at
rest. If you give it a velocity, currents induced in the pipe will exert a
force on it which causes it to stop.
 QUESTION:
QUESTION:
When calculating the frequency of a radiowave, the formula to use is: frequency = c / wavelength. However, if the wavelength is 12mm, and we assume c to be rounded up to 3 x 10^8, when I get the answer 25,000,000, how do I know if this is in hertz or kilohertz?
I've used online calculators to check the answer and it corresponds to 25,000,000 kilohertz but I want to know why was the figure 25,000,000 in kilohertz and not hertz.
 ANSWER:
ANSWER:
You can understand what is going on by showing the units
in your calculation. f=c/λ=(3x108 m/s)/(12 mm)=0.25x108
m/(mm∙s). If you had used consistent length units, not mixed millimeters and
meters, the length units would have cancelled out. For example, writing
λ=12x10-3 m,
f=c/λ=(3x108 m/s)/(12x10-3
m)=0.25x1011 s-1=0.25x1011
Hz=0.25x1008 kHz. Scientists
usually try to get everything into the same system of units before doing any
arithmetic.
 QUESTION:
QUESTION:
If an astronaut caught a ball in space, the ball would cause the astronaut to move backwards with the force the ball was moving at correct? then, as the astronaut is still moving backwards and throws the ball back where it came from, would the astronaut move even faster with the force of throwing the ball? or would their speed remain the same?
 ANSWER:
ANSWER:
When she catches the ball, she exerts a force on it to
stop it (relative to her); the ball exerts an equal and opposite force on
her causing her (and the caught ball) to move in the direction the ball was
originally moving. When she throws it back, she must exert a force on it
opposite the direction she is moving; the ball
exerts an equal and opposite force on her
causing her to move even faster in the direction she was moving. These are
examples of Newton's third law.
 QUESTION:
QUESTION:
If one were in a deep hole 100 miles from the center of the earth, would gravity at that point be less than at the surface of the earth?
 ANSWER:
ANSWER:
Yes. Here is the reasoning: if you have a spherically
symmetric mass distribution, meaning that the density does not depend on
longitude and latitude, the only mass which contributes to the gravitational
force if you are inside the sphere is the mass inside the sphere where you
are. So, if you are at the center of the sphere, there is zero gravitational
force. An interesting historical note is that this problem was one of the
more important reasons Newton had to invent calculus. He had to show that a
spherically symmetric mass distribution had the same gravitational field
outside as if the mass (a planet, for example) were a point mass at its
center. I have read that struggling with this problem caused the publication
of his gravitational law to be delayed by 20 years. (I do not really know if
that is true or not.)
If, in addition,
the mass distribution is uniform, the density does not depend on how far you
are from the center, you can easily calculate how the gravitational force
varies inside. Outside the force on a mass m due to the earth with
mass M is GmM/r2 where r is how far
you are from the center. Inside, the mass below you can be written M'=M(4πr3/3)/(4πR3/3)=M(r3/R3)
where R is the radius of the earth. So the force inside is GmM'/r2=GmMr/R3
which decreases linearly as you go in.
 QUESTION:
QUESTION:
I read that the average person can tolerate about 5 g-force before they black out.
Hypothetical: if every atom of air around you (and those of the Earth below) emitted 5 times their normal gravity, would this be harmful? or because it's pulling from all directions would the forces kind of cancel out?
 ANSWER:
ANSWER:
Essentially, you are asking what if the earth had the
same size and five times the mass; also the air were made of molecules five
times more massive than normal atmosphere. If your weight now is 200 lb,
your new weight would be 1000 lb and your legs would likely not be able to
hold you up. The pressure of the air around you would be greatly increased
and that pressure would likely be what would kill you, not the weight of
your body. (Since gravity is 5 times stronger and the mass of air molecules
is five times greater, I am guessing that the atmospheric pressure would be
about 25 times greater.)
 QUESTION:
QUESTION:
What is mass?
 ANSWER:
ANSWER:
There two kinds of mass. Inertial mass is the property an
object has which resists acceleration when a force is applied; the harder it
is to accelerate something, the more inertial mass it has. Gravitational
mass is the property an object has which allows it to feel and create
gravitational forces; for example, the more gravitational mass an object has
the greater the force it will feel due to the earth's gravity�the more it
will weigh. It turns out that the two masses are actually identical; this
fact is one of the cornerstones of the theory of general relativity.
 QUESTION:
QUESTION:
What is the formula to calculate the total energy of an object that is moving at relativistic speeds? (Ignoring any potential energy)
 ANSWER:
ANSWER:
E=√(m2c4+p2c2)
where p=mv/√(1-v2/c2) is the
linear momentum, m is the rest mass, v is the speed, and c
is the speed of light. This can also be written as E=mc2+K
where K is
the kinetic energy (which is not �mv2). Comparing these two
expressions and doing some algebra, you could find an expression for K.
Also, it may be written E=mc2/√(1-v2/c2).
 QUESTION:
QUESTION:
As I understand
one particle and an antiparticle would, if they come in contact completely, annihilate each other and turn in to energy equaling the mass of both of the particles.
But if a particle is moving at close to 1c relative to the observer and the other particle was not moving, the speeding particle would have a relativistic mass.
In other words the mass of both particles were not balanced.
Would the larger mass of one particle result in more energy, or creation of some other particles?
Or would the extra mass from the speeding particle simply transform to normal kinetic energy?
 ANSWER:
ANSWER:
The questioner used hydrogen-antihydrogen as an example;
I have edited this out since those are composite particles and just muddy
the water when trying to discuss what could happen. The most common example
is the electron-positron pair. If they interact at low speeds the only thing
which is possible is the creation of two (or more) photons because there is
not enough energy available to create more massive particles. If one (or
both) of the pair have significant kinetic energy when they collide, other
particles may be created as the questioner suggests. There are selection
rules which restrict which kinds of particles may be created, but if there
is sufficient energy just about anything allowed could happen�the constraint
is that energy must be conserved. In this kind of collision, though, you
must also conserve momentum. For example, suppose that you wanted to collide
very high-energy positrons with electrons at rest and create a pair of
particles with total rest mass M+2me where me
is the electron (or positron) rest mass. Your first thought might be that
the kinetic energy of the positrons would need to be Mc2.
But this would not work because the particles would have to be at rest which
would violate momentum conservation; so the energy would have to be
considerably larger. Proton antiproton interactions are considerably more
complicated because they have sufficient rest mass energies to create
massive particles even at rest and because they, unlike electrons and
positrons, are composite particles made up of quarks. They usually
annihilate into mesons which, being unstable, decay ultimately to some
combination of gamma rays, electrons, positrons, and neutrinos.
 QUESTION:
QUESTION:
when a drop of water is dropped on to a hot iron plate why does it become spherical before evaporating?
 ANSWER:
ANSWER:
Any place where the water touches the plate the water
will almost instantly vaporize. But the water must touch the plate for the
weight of the drop to be held up. The result of these two competing things
is that the water touches the plate only in a very small area. It is not
spherical, but close enough to look that way.
 QUESTION:
QUESTION:
Is it mere observation that light has the same speed in every frame of reference? Or, is there any deeper reason?
 ANSWER:
ANSWER:
Very deep! Read the FAQ
page.
 QUESTION:
QUESTION:
Outside the nucleus, free neutrons are unstable and have a mean lifetime of 881.5�1.5 s. What is it in the nucleus that keeps the neutrons stable?
 ANSWER:
ANSWER:
Although somewhat simplistic, you might think of neutrons
as stuff inside a nucleus which keeps the protons from getting too close to
each other so the Coulomb repulsion will not blow it apart. There is no
stable nucleus (apart from 1H) composed of only protons. On its
own, a neutron will beta-decay; quite simply, this is determined by
energetics�energy is released if a neutron decays into a proton, a neutrino,
and an electron. To find out what happens inside a nucleus, you again look
at energetics; if a neutron inside a stable nucleus were to decay, energy
would have to be added, so it does not happen.
 QUESTION:
QUESTION:
My question is for a legal nature. I was recently in a head on collision. The crime scene analysis could not determine the speed of my vehicle but police reports indicated the other vehicle was doing 45+- mph. We were on a dirt road on impact. The vehicle going 45+- continued to travel 20 ft past impact pushing my vehicle back 40 ft. His vehicle is a 1 1/2 ton dodge ram and my vehicle was a 1 3/4 ton dodge caravan. What speed was my vehicle? This will be instrumental in a lawsuit currently being filed. Your help would be greatly appreciated.
 ANSWER:
ANSWER:
I am afraid that the speed cannot be determined from this
information for several reasons:
-
I do not know how much energy
was lost in the collision.
-
I do not know whether the
wheels were locked (brakes applied) or not.
-
I do not know the frictional
forces which ultimately brought the vehicles to rest.
-
I believe the weight of the
Dodge Ram is wrong. The Dodge Ram 1500 is referred to as 1�
tons because this is the maximum recommended load. An unladen Ram 1500
weighs more than 6000 lb; I found that the weight of the Caravan is
about 1.75 tons, though.
 QUESTION:
QUESTION:
If a capacitor stores large amount of charge then can it be considered as a battery??
 ANSWER:
ANSWER:
In the sense that it can provide a steady potential
difference, yes. In the sense that it can provide a steady electric current,
no. As soon as you begin trying to take energy from the capacitor, its
potential difference begins to fall.
 QUESTION:
QUESTION:
Friction opposes the relative motion between two surfaces. when a car travels on a circular path , how can the friction act sideways to provide necessary centripetal force. The friction should act backward relative to the motion of the car. the car doesn't tend to go sideways outward, then, how does friction act sideways?
 ANSWER:
ANSWER:
There are two important classes of friction, kinetic
friction which occurs when two surfaces are sliding on each other and static
friction when they are not sliding. Kinetic friction is the one which
usually (but not always) acts opposite the direction of motion; an example
of kinetic friction acting in the direction of motion is a car which is
accelerating from rest and spinning its wheels�the friction force on the
spinning wheels by the road is forward. Static friction can point in any
direction, depending on the situation. If a box is sitting at rest on an
incline, the frictional force points up the incline to keep it from sliding
down. If a car is moving but not skidding, the appropriate friction to think
about is the static friction between the wheels and the road. Think
about a very icy road; to drive around a curve at high speed is impossible
because there is no static friction and the car simply continues going
straight regardless of whether you turn the steering wheel or not.
 QUESTION:
QUESTION:
Gravitational potential energy is the term
that means the work done by the gravitational force to take an object to the gravitational field. Here the displacement is towards the force.So,it (Gravitational potential
energy) should be positive.But it is negative.Why?
 ANSWER:
ANSWER:
You need to be a little more careful in how you define
potential energy. And, what is actually defined is the potential energy
difference between two points in space. The definition is ΔU=U(r')-U(r)=-
r∫r'F∙dr,
where F is the force of gravity on m due to the
presence of M. Now, if I choose increasing r to be in the
upward direction,
F∙dr=-(MmG/r2)dr.
So, -r∫r'F∙dr.=-r∫r'[-(MmG/r2)]dr=-MmG[(1/r')-(1/r)]=U(r')-U(r).
This is completely general. It is customary to choose U(∞)=0, so if
r'=∞, U(r)=-MmG/r. (You have to be very
careful of all these minus signs!) So, you see that the potential energy is
determined by where you choose it to be zero and the choice of coordinate
system; if we had chosen r to increase in the downward direction and
U=0 infinitely far away (at r'=-∞), U would have been
everywhere positive.
 QUESTION:
QUESTION:
Could fusion energy be powered by other
hydrogen isotopes or other light elements?
 ANSWER:
ANSWER:
Yes, fusion produces energy up until you get around iron
as the final fusion product. Thereafter it costs energy to fuse nuclei.
However, the general trend as you go to heavier nuclei is that the
fractional energy output compared to mass gets smaller. Another problem if
you are thinking of a reactor is that heavier nuclei have higher electric
charge and are therefore harder to bring close enough together to fuse.
 QUESTION:
QUESTION:
I read a fact that a compressed spring weighs more than a relaxed spring...why is it so??
 ANSWER:
ANSWER:
It is true but unmeasurable. Suppose the spring constant
is k=2,000 N/m and you compress it by x=1 cm=0.01 m. The work
you did is E=�kx2=0.1 J. This energy will end up as added
mass m=E/c2=10-18 kg.
 QUESTION:
QUESTION:
I was reading a novel the other day which takes a surprisingly realistic approach to theoretical space-combat (namely ships attacking each other with missiles from many millions of kilometers away), albeit with missiles moving at significant fractions of the speed of light (around 30-40%).
This made me wonder, say two space ships are fighting and one fires a missile traveling we'll say 50% the speed of light. I'm having real trouble understanding the effect time-dilation would play (and the author completely avoided the subject). I tried reading some of your past answers on time-dilation, but I just ended up confusing myself.
My thought is that the missile which is traveling at the significant fraction of c (while the ship is not) would have a huge advantage. With time passing slower the missile would have the net effect of having more time available to itself; to which it could use to account for the ship's attempts to evade, to itself evade any counter-measures the ship might employ, all in addition to being difficult to detect and track due to its speed.
Would the theoretical missile in this situation have those benefits, and the target ship be suffering a serious disadvantage; or does time-dilation not work that way?
 ANSWER:
ANSWER:
Time dilation really does not come into play here if I
understand things correctly. If you are thinking that the missle is robotic
and able to adjust to evasive movement of the target, there is no advantage
because the missle sees the distance to the target shrink by the same factor
that its clock slows down. As seen from the stationary fleets, there is just
a projectile with half the speed of light. Since the speed of light is
300,000 km/s, the attacked fleet will observe the missle coming with a speed
of 150,000 km/s and many million kilometers, let's say 150 million for
illustration, means that it will take 1000 s to get to the target as
measured by the fleets. The target fleet will not know it has been attacked
until 500 s before the missle arrives, but that still gives time for evasive
action. The main problem is that because of the high speed, evasive action
becomes increasingly difficult as the missle gets close but this has nothing
to do with time dilation. The advantage to the missle is due to its high
speed and the limited reaction time of the target.
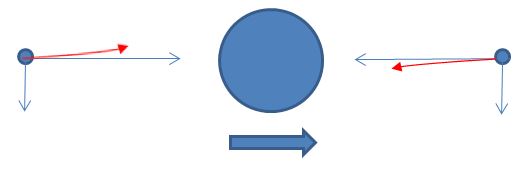
 QUESTION:
QUESTION:
ok, two stones. Both spherical and same mass and
density evenly spread in each stone. Set each about 1/2 the distance to the
moon. One leading the earth's orbit and one following the earth's orbit.
Both not moving relative to the earth, yet the same speed as the earth as it
moves around the sun. No tangent or orbital speed, the stones are starting
in freefall. Which gets to earth's surface first, neglecting
air drag.
 ANSWER:
ANSWER:
Since you stipulate that the stones are not
orbiting, the stones are at rest with respect to the sun and the earth is
not. Therefore, the stone on the leading side of the orbiting earth will win
the race because the earth is moving toward it and away from the other when
the stones start dropping.
 BETTER
ANSWER:
BETTER
ANSWER:
I see that I misread this question. I guess you meant there is no orbital
speed around the earth. To make this manageable at all I will neglect the
influence of the moon and assume a
spherically-symmetric mass distribution of the earth. In the figure
above, I show your two stones and the forces (blue arrows) on them. The
down-pointing forces are the from the sun (keeping them in orbit) and the
horizontal forces are the weights making them want to fall toward the earth.
The distances and forces are not drawn to scale; when the stones are about
30 earth radii away from the earth center (the moon is about 60 earth radii
away), the weight forces are about 2 times larger than the sun forces. The
big blue arrow shows the direction everyone is orbiting the sun. So, the
leading stone slows down its orbital speed and so will slightly fall toward
the sun as it falls toward the earth; the trailing
stone increases its orbital speed and so will slightly fall away from the
sun as it falls toward earth. These deflections are shown (probably quite
exaggerated) by the red arrows. Given the symmetry of the situation, I
would expect the two to be at the same distance from the center of the earth
at any given time�which is the
crux of your question, I think. To actually do this more quantitatively,
though, would be very hard because as the stones were deflected the weight
force would change direction now having a vertical component in the figure.
 QUESTION:
QUESTION:
Physics is my hobby, but, language is my education (MA).
I realized a while ago that there is no definition for motion beyond "when
something goes from point a to point b". There are archives of
"descriptions" of motion (e.g. Newton), but no "definition". After 3 years,
I have found a definition! So, what do I do? Journal article? Copyright?
Show up at some place and submit my idea? Please assume that what I am
saying is true.
 ANSWER:
ANSWER:
The reason that you cannot find an operational definition
is that there is none. There are generally two types of concepts in science,
quantitative and qualitative. If you are a "language guy" you must
understand that. Qualitative concepts are those which we understand in terms
of language, they are not quantitatively defined. Everyone understands that
motion is when something moves to some other location in some time. Asking
what the definition of motion is is like asking what the definition of wet
or large or speedy is�there is none. For motion, though, there is an archaic
definition. When Newton stated his second law he wrote it as �The alteration of motion is ever proportional to the motive force impress�d".
Today "alteration" is stated as "rate of change", "motion" is "linear
momentum" which is mass times velocity, and 'motive force" is simply
"force", so rate of change of momentum (d(mv)/dt) is
proportional to force. So, you might satisfy yourself that motion is mv
where m is operationally defined (kilogram, e.g.); v is
rate of change of position, a length divided by a time and both length
(meter, e.g.) and time (second, e.g.) are operationally
defined. Again I emphasize that this is archaic and motion today is
qualitative.
 QUESTION:
QUESTION:
I have a 10' long trailer I am using to haul a 4,000# symetrical object that is 6 ft in length. I was told to move it forward of the axle on the trailer to put some weight on the tongue for safety and better hauling. The maximum wt my pick up truck can hold on its hitch is 650#. I have tried to find equations for this on-line as it would be very useful for me to know how to adjust other loads as well. There are plenty of equations on-line that deal with finding the CG, but I can't find one that discusses how the weight on the tongue changes as the load is moved fore or aft of the axle. Trailer/towing experts just wing it. Do you know of an equation that would help me?
 ANSWER:
ANSWER:
I will assume that the unladen trailer will have
approximately zero force on the hitch (which would mean that its center of
gravity (COG) is at the axle). You need to know where the COG of the load is; in your
specific case, you know that it is at the geometrical center (you said it is
symmetrical), 3' from either end. For loads not symmetrical, you need to
find it. I will call the distance between the axle and the hitch L.
Suppose that the COG is a distance x from the hitch. Then, the sum of
the torques about the axle must be zero, so Hx=W(L-x) where H is the force (up) by the hitch and
W is the weight (down) of the load.
Solving this, x=[W/(H+W)])L. For your case, with
H being 650 lb (although I cannot see why the maximum would be the
optimal) x=(4000/4650)L=0.86L. If your
trailer has more than one axle or its COG is not over the axel, I would need
more information like the geometry and weight of the trailer.
 QUESTION:
QUESTION:
When I have a rope attached to a vertical wall and a climber using the rope to climb perpendicular to the vertical wall,as the climber goes up the rope the tension in the rope increases, Why?
 ANSWER:
ANSWER:
To move upward you must pull down on the rope and that
pull increases the tension.
 QUESTION:
QUESTION:
What effect (if any) would there be on the solar system if the sun were to lose the mass of Jupiter? This question is based on various schemes to power a "warp drive" by converting mass about the size of the planet Jupiter into pure energy. Since vaporizing Jupiter is probably not a good idea, it might make more sense to get the necessary mass by skimming off a chunk of the sun's surface. Assuming mankind might have the technology to do this someday, would the sun be appreciably different if it lost the mass of Jupiter? Would the orbits of the planets change to a significant degree?
 ANSWER:
ANSWER:
I usually do not answer astronomy questions, but will
take a stab at this one since I have
earlier talked about effects
which Jupiter has on other objects in the solar system. If Jupiter
disappeared it would have a negligible effect on other planets. It would,
though, have a large impact on many asteroids whose orbits are controlled by
Jupiter's gravity (see that earlier
answer). This would release a swarm of asteroids into earth-crossing
orbits considerably increasing the likelihood of catastrophic collisions
with earth. The mass of Jupiter is only 0.1% that of the sun, so taking that
much mass from the sun would probably cause fairly minor effects on solar
system orbits. "Skimming" that much mass from the sun could have pretty
serious short-term effects on the sun's radiation. Oh, by the way, there is
no such thing as warp drive! (PS your email server
rejected my mail as spam.)
 QUESTION:
QUESTION:
I've been arguing with a friend about this, and I'm sure you've answered it before, but I spent about 30 minutes searching the web and I couldn't find anything! So to the question, if one were to make a "phone" out of a paper/styrofoam/tin cup connected to a string, would it work in space? I believe it would because the strong would act as a medium.
 ANSWER:
ANSWER:
Yes and no. If you tapped on one cup that vibration would
be transmitted via the string to the other cup. But if what you had in mind
is speaking into one end and someone hearing on the other end, it would not
work because your voice is sound in the air which gets the cup vibrating and
there is no air.
 QUESTION:
QUESTION:
A 5.0 Mev electron makes a head-on elastic collision with a proton
initially at rest. Show that: a) The proton recoils with a speed
approximately equal to (2Ee/Ep)c
and
b) the fractional energy transferred from the electron to the proton is (2Ee/Ep), where
Ee is the total incident energy of the electron and Ep is the rest energy of the proton.
 ANSWER:
ANSWER:
I have verified that this is not a homework problem. The
solution may be seen here.
 QUESTION:
QUESTION:
The definition of "electric current" I find in my school books is: "directed flow of electrons". The power stations here in my country use hydro power to make work some huge generators which create electricity, i.e directed flow of electrons. But their functioning is not based in obtaining electrons from something (not the water nor the metal), instead its function is to create some magnetic fields which seem to be essential in creating electric current.
My question: Is the above definition of electric current correct? If yes, where do the continuous flow of electrons come from? Are really magnetic fields a limitless source of electrons, if not, how do they generate limitless electricity?
 ANSWER:
ANSWER:
The electrons which flow in a wire were already there
before the current started. In materials which are conductors there are
electrons which are very easy to move around. Magnetic or electric fields
may be used to cause these "conduction electrons" to move. Electrons are not
being injected into the wire.

 QUESTION:
QUESTION:
Here's a question that I have been pondering. If a truck is driving on the freeway and a car pulls in closely behind the moving truck to take advantage of the draft created by the truck is there an energy cost to the truck or is having a car in it's wake energy neutral?
My gut feeling is that there would be a slight energy cost to the truck due to it's turbulence wake being interfered with.

 ANSWER:
ANSWER:
This, I discovered, is not a trivial question. For a
lengthy discussion, see
The Naked Scientists. Here is my take on it. There is no question that
the trailing car consumes less gas. The reason for this is not so much that
the truck is pulling the car but that the car experiences a much lower air
drag when drafting; the drag is approximately proportional to the square of
the velocity and the truck's wake is moving forward with the truck. What
seems to be controversial is the crux of your question—is
there a cost to the truck? Some argue that the composite truck-car system
has less total air drag, others that there is a net cost to the truck which
need not (and almost certainly will not) equal the gain by the car. There is
certainly no conservation principle here because the new system has
different forces on it than the separate systems. My feeling is that there
is at least a small cost to the truck and I base this on an observation from
nature. Why do geese fly in a V? There is less overall air drag than if the
flock all flew individually. But periodically, the leader drops back and
another goose takes a turn at the front; must be because the leader has to
do more work.
 QUESTION:
QUESTION:
A
friend asked me this and we disagreed with the answer.
If we put 25 kg of weight on top of 25 kg person, how much force would he
feel?
 ANSWER:
ANSWER:
Technically, a kilogram is not a weight but a mass. But,
since so many countries use it as a weight, I will do that for this problem.
The person feels the downward force of her own weight, 25 kg; the downward
force of the object pushing down on her, 25 kg; and the upward force of the
floor pushing up on her, 50 kg. The net force is zero because she is in
equilibrium.
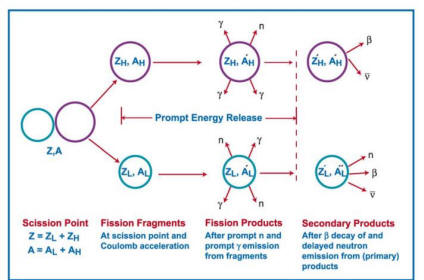
 QUESTION:
QUESTION:
Is there a speed or time measurement for how long it takes the nuclei of Uranium or Plutonium to transfer from Matter to Energy in nuclear fission after the neutron has split the atom?
 ANSWER:
ANSWER:
I found a
paper which
lists the "prompt energy release time" as in the range of 10-20-10-7
s. This is the time between the scission and the end of prompt gamma rays
and neutrons. I presume this huge range is because of dependence on the
fissioning nucleus and the fission products.
 QUESTION:
QUESTION:
If
an object approached a plane mirror at 3/4 the speed of light, would it be
approaching its image at 1.5 times the speed of light?
 ANSWER:
ANSWER:
No, because the image does not exist. Light leaves you
and travels to the mirror at the speed of light and then the reflected light
comes back to you at the speed of light. The light you emit and the light
you receive would both be doppler shifted toward the blue so what you saw
would not be true color.
 QUESTION:
QUESTION:
A parallel plate capacitor has a small gap between its two plates , then how it completes the circuit when it is connected by a battery?
 ANSWER:
ANSWER:
Current flows until the capacitor is fully charged and
then it stops. So, except for a short time when you first connect to the
battery, it acts like an open circuit.
 QUESTION:
QUESTION:
Has any human been more then 1,000,000,000 miles in space and returned?
 ANSWER:
ANSWER:
The farthest any human has been is the moon which is
about 240,000 miles from earth.
 QUESTION:
QUESTION:
I'm in a space ship moving at the speed of light. I put my space suit on, go out on the deck of the ship and tee up a golf ball. Assuming I have the skill necessary to hit the ball, will I be able to hit the ball forward? It seems to me that in the vacuum of space, the energy required to hit the ball forward would not change with my vehicle's speed, but it's also my understanding that the speed of light is an absolute maximum speed. One of these is apparently wrong. I think you are going to tell me I can't hit the ball forward. Can you explain why?
 ANSWER:
ANSWER:
As I have said a thousand times, you cannot move at the
speed of light. See the faq page if you
have a problem with this. However, we can address your question by saying
your ship has a speed 99.999% the speed of light u=0.99999c.
Suppose that you can launch a golf ball at a speed of 10% the speed of
light, v=0.1c. (Of course, it is impossible to make it go that
fast because you are not strong enough, but it makes this example easier to
quantify.) If you were able to do this, there would be absolutely no reason
why you could not do it on the moving ship: you would simply see the ball
move away from you with speed of 0.1c just as if you were here on
earth. Now, classical physics (and your intuition) would have the speed seen
by someone watching this to be V=(0.99999+0.1)c=1.09999c,
almost 10% faster than the speed of light. However, classical physics does
not work here; again, see the faq
page. Instead, V=(0.99999+0.1)c/(1+0.99999x0.1)=0.99999182c.
 QUESTION:
QUESTION:
Is there a magnetic field or not?
If there is a charged particle with no velocity relative to viewer A there is no current and no resultant magnetic field, right? But if the same particle is viewed by another observer moving at some velocity relative to it then it could be said the particle is moving at -v and should show both a current and magnetic field.
How can you reconcile this?
 ANSWER:
ANSWER:
Let me pose an analogous question. Is there a velocity or
not? If there is a particle with no velocity relative to viewer A there is
no velocity, right? But if the same particle is viewed by another observer
moving with some velocity relative to it, then it could be said that the
particle is moving with some velocity. How can you reconcile this? Like most
observables in nature, magnetic fields depend on the frame from which they
are observed and, in some special cases like your example, you can actually
find a frame in which the magnetic field is zero. In your example, if the
observer moves with speed 100v, the magnetic field will be much
stronger than if he moved with speed v. Electric fields also behave
this way and the electric field observed by the moving observer in your
example will differ from the field seen in the frame where the charge is at
rest. Actually, there is only one field, the electromagnetic field; the idea
of separate electric and magnetic fields is a historical artifact. You might
be interested in a similar question about electromagnetic radiation fields.
 QUESTION:
QUESTION:
My brother and I recently had a lively debate about the mechanics of temperature change within a glass of ice water (i.e. tap water sharing a glass with ice cubes). My brother remembers a Physics professor saying that the temperature of the (liquid) water within the glass won't change until the ice completely melts. Contrarily, I believe the temperature of the water within the glass begins changing immediately (after the liquid water has settled in the glass with the ice). Can you enlighten one (or both!) of us?
'
 ANSWER:
ANSWER:
Imagine doing the experiment in a well-insulated cup; a
styrofoam coffee cup would be a fair approximation. I just want to not worry
about the interaction with the rest of the environment. The tap water is
certainly warmer than the ice. What we know for sure is that if two objects
are in contact with each other, heat flows from the hotter to the colder.
So, heat flows from the water (cooling it) into the ice. This energy
absorbed by the ice is used to melt some of the ice meaning that some water
at 00C mixes with the already-present water making it cooler yet.
This continues until all the ice is melted (or all the ice and water is at 00C) and the whole system is now at a
considerably lower temperature than when you started. But, if you have ever
made and drunk a glass of ice water it should be obvious that your brother
is wrong�the water is much colder than tap water shortly after the ice has
been added and long before all the ice has fully melted. What does not change is
the total energy inside the cup.
 QUESTION:
QUESTION:
I'm having a little debate right now that centers around my stance that materials will have a large role on the crash results of an auto accident vs my opposition that says that materials do not matter and that a moving object will take more damage b/c its hitting a non-moving object.
Situation: A 3,900 pound 1983 steel mercedes benz going 30 mph were to impact a primary plastic SUV that weights 4,100 pounds and its going 10 miles per hour perpendicular to the Mercedes (it ran a red light) after we both slammed on our brakes.
So what happens when 2 object hit. Do you add up the net speed of 30 plus 10 to say that both get hit at 40 miles per hour?
 ANSWER:
ANSWER:
There is really not enough information to say
definitively. Also, your preliminary remarks about materials and non-moving
do not really address the question you pose afterward ("what happens?")
Suppose the two stick together (called a perfectly inelastic collision).
Then you need to conserve momentum, mass times velocity. Before the
collision the Mercedes has 3900x30=117,000 units of momentum say north; the
SUV has 4100x10=41,000 units of momentum say east. The net momentum after
the collision is √(1170002+410002)=124,000=(3900+4100)V=8000V,
so the speed V is about 124000/8000=15.5 mph. The direction of the
velocity afterwards is mainly northward with a small eastward component.
Brakes were probably applied too late to change any speed by much, would
hasten the stopping of the collided cars. Certainly the composition of the
cars will affect the damage each suffers.
 QUESTION:
QUESTION:
Does the velocity and direction of wind make any difference to sound wave ? and if it does , how much?
 ANSWER:
ANSWER:
Suppose you have a source of sound which emits sound
waves with a velocity Vsound in still air. Now
suppose that there is a wind with velocity Vwind.
The new velocity of the sound (relative to the ground) is
V=Vsound+Vwind.
Be sure to note that this is a vector equation.
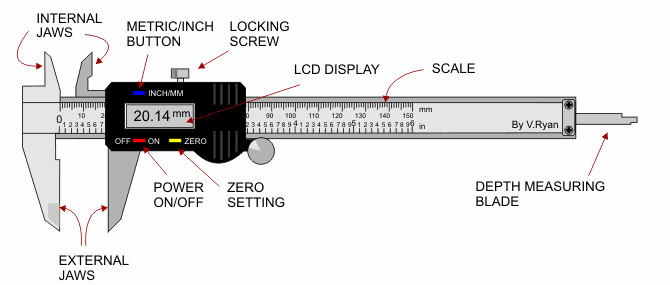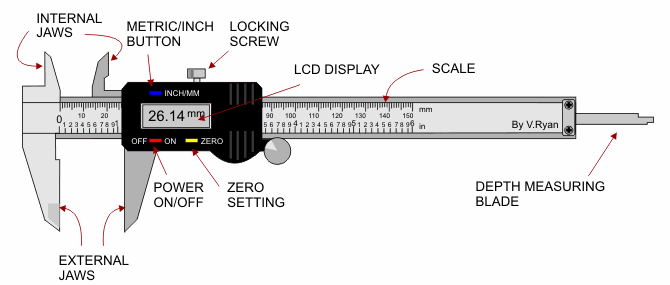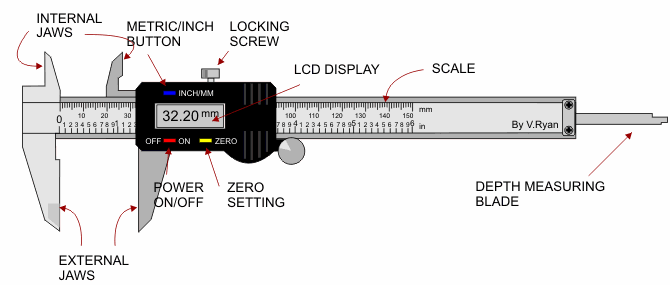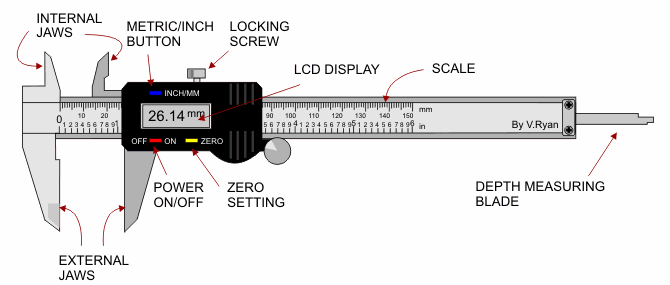
 QUESTION:
QUESTION:
What is a vernier calliper?
 ANSWER:
ANSWER:
An instrument to measure lengths. See the figure to the
right.
 QUESTION:
QUESTION:
The less density an object has the more it
rises in the atmosphere but i was wondering why doesnt it rise at all if it
has zero density . I mean zero kg per m3 ..which means a vaccum
or a vaccum chamber.
 ANSWER:
ANSWER:
It is the overall average density which matters, not the
density of just what is inside a container. If the weight of the whole
vacuum chamber is less than the weight of an equal volume of air it will
rise.
 QUESTION:
QUESTION:
I want to ask that scalar quantities can also be negative i.e. time is negative if it is before origin and positive after origin . Then distance should also follow the same rule. now suppose in case of straight line motion a body covers first +5 units and then-5 units. Then whether the distance will be 10 or 0. I know that it should be 10 but according to the first statement it should be 0. if it is 0 then what is the distancebetween distance and displacement
 ANSWER:
ANSWER:
Certainly, some scalars can be negative. For example, as
you note, time before t=0 is negative. Or, temperature on the Celsius
scale below zero is negative. However, the magnitude of a vector is positive
definite. Your example of a distance being negative is not really correct.
In one dimension the distance is the magnitude of the displacement vector
and the direction of the vector is determined by the sign.
 QUESTION:
QUESTION:
"Tritium is produced in nuclear reactors by neutron activation of lithium-6" my question would be; If lithium-7 (the product of the neutron capture) is a stable isotope why does it split? And is this splitting α decay, or fission, that just happens to result in an alpha particle
& a tritium nucleus?
 ANSWER:
ANSWER:
Because the 7Li does not get formed in its
ground state, rather it is highly excited. Or, you might want to look at it
as a nuclear reaction since it happens very quickly: 6Li+n->4He+3H.
It is not surprising that this reaction goes because the alpha particle is
extraordinarily tightly bound; that is one of the reasons heavy nuclei often
undergo alpha decay�because it is such a tightly bound nucleus, there is a
reasonable probability that it will spontaneously form inside a nucleus.
 QUESTION:
QUESTION:
If you have a boat floating in a bowl of water and you increase gravity , does it float even more or does in stay at the same place ?
 ANSWER:
ANSWER:
If you increase g, the buoyant force, the weight of the
displaced water will increase by the same amount. But, the weight of the
boat will increase by the same amount and float the same.
 QUESTION:
QUESTION:
Given that a proton has a magnetic dipole moment, do researchers currently use magnetic field to rotate them in addition to accelerating them to further increase the energy of their collisions?
 ANSWER:
ANSWER:
A magnetic field exerts a torque on a dipole, but no
force. So you cannot use a magnetic field to accelerate them.
 QUESTION:
QUESTION:
If an ultra high energy cosmic ray with energy of 1020
eV were to strike an astronaut will that kill an astronaut?
 ANSWER:
ANSWER:
This is only about 6 J of energy. That is the energy
needed to lift 1 kg about 60 cm. And, it would probably not leave all its
energy in the astronaut. Certainly would not kill her.
 QUESTION:
QUESTION:
if you have 3 flywheels of the same material, with the same dimensions, and attached to similar engines. The wheels all have equal amounts of weight... one with the weights in the center, one with the weight at the outside of the wheel, and the third one with the weight between the center and the outside. If all three engines are running for the same time and the same speed and the power is shut of simultaneously, which one will spin the longest?
I ask this because I am studying for a firefighter test and they have given me wrong answers before. According to the book they say the wheel with the weight on the outside, however i think back to my high school physics class and the example of the figure skater that spins faster with their arms tucked in.
 ANSWER:
ANSWER:
The issue here is how much energy each flywheel has. If
the angular velocity of a rotating object is ω and its moment of
inertia is I, then its kinetic energy is �Iω2. The
quantity called moment of inertia depends on how much mass there is and how
it is distributed. For example, the flywheel with most mass far from its
axis is harder to get rotating or stop rotating than if most of the mass
were close to the axis. Suppose we model the three flywheels as rings of
mass M and radii R, R/2, and R/10; the moment of
inertia of a ring is MR2, so the moments of inertia would
be MR2, MR2/4,
and MR2/100 respectively. Therefore with equal starting
rotation rates, the energy of the largest ring would be bigger by factors of
4 and 100 than the other two. Your figure skater is an example of angular
momentum, Iω; if she pulls in her arms, her
moment of inertia decreases and so her angular velocity must increase to
keep angular momentum constant. For the three rings, angular momentum of the
largest ring is bigger than the other two by factors of 4 and 100 just like
for the energies.
 QUESTION:
QUESTION:
I have been searching all over the internet to find out how to calculate how much wind it would take to move and lift a person, car or other things i might find interesting? I do not have any background in physics, but basic knowledge of maths. so could you give me some god insights to what mechanic's that are in play, and how they work I would be gratefully thankful.
 ANSWER:
ANSWER:
To vertically lift something you would have to know its
terminal velocity when falling; that would be the upward wind velocity
necessary to levitate it. For example, the air drag force on a ball is about
f=0.22D2v2 where D is its
diameter in meters and v is its speed. A basketball has D=0.24
m and a mass m=0.62 kg, so the weight is mg=0.62x9.8=6.1 N and f=0.11x.242v2=0.013v2.
Since f is the force up of the wind, to levitate the basketball the
speed must be v=√(6.1/0.013)=21.7 m/s=22 m/s=49 mph. If there were no wind
and the ball were falling, this would be the maximum speed it would achieve.
To move something horizontally would require that you specify a lot more
than its size and shape; you can see this since it is a lot easier to move a
box on ice than on concrete, for example.
 QUESTION:
QUESTION:
How would you go about calculating the work done on an object being pushed up a curved inclined plane? Do you have to use calculus?
 ANSWER:
ANSWER:
If friction is negligible, all that matters is how high
you lift the object, not the path you took. If there were friction you would
have to use calculus, know the mathematical shape of the path.
 QUESTION:
QUESTION:
If an object (a ball) is thrown vertically, will the air resistance of both sides of the trip (upwards and then downwards) cancel themselves out, giving the exact, but mirrored, travel time/travel speed/etc. for both sides of the trip? Or will the slowing-down effect of friction give a slower velocity, and a longer descending time, for the second half of the ball's trip?
 ANSWER:
ANSWER:
No. The motions in the two directions have different
dynamics. The two forces on the ball are its weight and the air resistance;
the weight is down for both up and down, but the air resistance is down on
the way up and up on the way down. Also, the air resistance depends on the
speed.

 QUESTION:
QUESTION:
I have a question releated to weight/mass placement on a bar. My friend and I are weight lifters. We got into a discussion about the center of gravity on the bar. Here is the question. If we are using a 45 pound plate on each side and also have a 5 and 10 on each side. Each taking up the same space and the end of the bar is the same distance from the last weight and will not change. Does it change anything if the weights are not in the same order, from one side to the other? My friend says the side with the 45 pound plate close to the end is slightly heavier becuase the ratio has changed. I say nothing has changed becuase the weights on the bar are still taking up the same space. I believe it would only change if the distance to the end of the bar is changed, which it is not. I hope I explained this
well enough.
 ANSWER:
ANSWER:
Assuming that the bar itself is uniform (has its center
of gravity (COG) at its geometrical center), the COG of the total barbell
depends on the location of the weights. Relative to the center of the bar,
the position of the center of gravity may be written as COG=(45x1+10x2+5x3-45x4-10x5-5x6)/120
where the xis are the distances of weights from the
center. Suppose that the weights are placed symmetrically (x1=x4,
x2=x5,
x3=x6);
then COG=0, the center of the bar. Now, suppose we interchange two of the
weights, exchange the 45 lb with the 10 lb on one side:
COG=(45x2+10x1+5x3-45x4-10x5-5x6)/120=(45x1+10x2-45x2-10x1)/120=(35/120)(x1-x2);
since x1≠x2,
COG≠0, the barbell is no longer balanced. If that explanation is too
mathematical for you, try a more qualitative argument. Each weight W
a distance D from the center exerts a torque about the center and the
magnitude of that torque is WD. The net torque due to all weights
must be zero if the bar is to balance at its center. This means that the sum
of all the WDs on one side must be precisely equal to those on the
other if the barbell is to be balanced about its center. If you change the
Ds on only one side, the bar will not be balanced at its center.
(This qualitative argument is just the mathematical argument in words.) What
certainly does not change is the total weight.
 QUESTION:
QUESTION:
I understand, if a twin leaves earth and accelerates at 1 g for 10 years, decelerates at 1 g for 10 years, turns around and comes back, accelerates at 1 g for 10 years, decelerates at 1 g for ten years, then, the space fairing twin�s clock would elapse 40 years and the earth bound twin�s clock would elapse 59,000 years. I understand the breaking of symmetry and the time dilation because of the space fairing twin�s acceleration (I think I do). My question is, is not the earth bound twin subject to the same 1 g of acceleration because of gravity, for the same duration? If both twins were in rooms with no windows, could one twin tell if they were the out bound or the earth bound twin? If both are experiencing 1 g, why the elapsed time difference?
 ANSWER:
ANSWER:
There are two kinds of time dilation, gravitational and
velocity. The first is very small if gravity is small and the earth's
gravity is small in this context; therefore, the acceleration of the ship is
really of no importance in your example. As you seem to surmize, the
gravitational time dilation for both observers will be the same; but since
the total time loss depends on the total elapsed time, the contribution for
the earth twin will be about 59,000 times a tiny number bigger than for the
moving twin (assuming that number is right). The second is very small if the
velocity is small compared to the speed of light; if you accelerate with an
acceleration g, eventually your speed will get big enough that there
will be appreciable time dilation; this will be the main contribution to the
clock discrepancies. I do not know where you got your numbers from, but they
could very well be right; certainly the 4 10-year times are right since they
are basically defined. It is complicated to calculate elapsed time for an
accelerated ship because it is always changing, but I will not get into that
because the answer to your question is that the gravitational shift will be
negligible for both observers. For detailed information on calculating how
to calculate the time dilation, see the reference in an
earlier answer. Also, another
of my earlier answers shows the speed of the
spaceship as viewed from the earth; note that this is not v=gt as you
might expect classically because the earth does not see the same
acceleration as the ship does.
 QUESTION:
QUESTION:
This question has bugged me for years. If the Moon orbits Earth every 28 days, then why the heck do we have 30-31 dqy months? Shouldn't we abridge our months to 28 days and add a thirteenth month to our year if we wanted our time measurement to be scientifically accurate?
 ANSWER:
ANSWER:
Seriously, you think the period of the moon's orbit has
anything to do with "time measurement�[being]�scientifically accurate"?
The unit of time, the second, is defined as "the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom".
In other words, time is defined by using an atomic clock and has nothing
whatever to do with any astronomical period. It is a lucky thing, too, that
time is no longer defined in terms of the orbital period of the earth (year)
or rotational period of the earth (day) or the orbital period of the moon
(roughly a month) because all these periods change over time. It was natural
for the ancients to measure time using naturally-occuring periodic events,
but we have "come a long way, Baby"! The definition of the months is a
historic relic and not to be taken as some kind of scientific standard. It
is interesting since the phases of the moon were related to agriculture and
the ancient Romans apparently had 10 months with a "two moon" period in the
winter when there was no farming; later two more months were added in the
winter, Januarius and Frebruarius. Many times in history the calendar was
revised as the year became better understood. If you are interested in the
history of time units, the ancient Egyptians divided day and night each into
12 time units, later the Greeks adopted a "mean hour" but still used a total
of 24 per day. The hour was subsequently subdivided sexigesimally (by 60)
into minutes, and then again into seconds. If you wonder about the frequent
appearance of the numbers 12 and 60, still the basis for angle measure, time
measure, and until recently the British currency, it is because having
numbers with many factors was convenient; 12 is divisible by 2, 3, 4, and 6,
60 is divisible also by 5 and 10.
 QUESTION:
QUESTION:
How come when visible light photons interact with electrons in an atom they simply move the electrons to higher energy levels however when photons of x-rays and gamma rays interact with the atom's electrons they're completely ejected from the atom (ionized)?
 ANSWER:
ANSWER:
The energy E of a photon may be written as E=hc/λ where h is Planck's constant,
c is the speed of
light, and λ is the
wavelength of the corresponding electromagnetic wave. Wavelengths of x-rays
and γ-rays are much shorter than for visible light and therefore they have
much higher energy, enough to completely remove electrons from atoms.
 QUESTION:
QUESTION:
Why does moving at very high speeds generate G-Forces?
 ANSWER:
ANSWER:
It doesn't. Having very large accelerations generates
large g-forces.
 QUESTION:
QUESTION:
We know, as we go deeper in a fluid the pressure increases and it's known that pressure is direct consequence of change in momentum of the fluid molecules, so can we conclude that as we go deeper in fluid the molecular velocity increases(as more is the velocity more is the force applied by collision or is my assumption wrong?
 ANSWER:
ANSWER:
The notion that pressure is related to molecular velocity
comes from the theory of ideal gases, and water is certainly not an ideal
gas. In a liquid, the pressure increases with depth because the deeper you
go, the more water there is above you, the weight of which is pushing down.

 QUESTION:
QUESTION:
After watching the Bond classic YOU ONLY LIVE TWICE, I read that the scene where a craft in space overtakes a capsule ahead in the same orbit in order to "swallow" it, but would be impossible because it would have to be in a separate orbit. Then when it catches up, turn vertical and move upward. Why is it not possible for an object to accelerate in the same orbit as a slower object?
 ANSWER:
ANSWER:
If the two satellites were in the same orbit, they would
maintain the same separation. If they were in different but crossing orbits,
you could have them come together if properly synchronized; if you were to
observe this, say from the perspective of the "chased" satellite, it would
appear that the other satellite was coming at you from slightly above or
below. Finally, if the "chasing" satellite had rockets which he could point
in any direction with any thrust, he could move exactly on the same path as
the "chased" satellite but with a different speed.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I don't grasp the physical law that would prevent the "chasing" capsule to catch up in the same orbit (as we see in the movie) if its thrusters accelerate it.
 ANSWER:
ANSWER:
It is easiest if we just think about circular orbits;
near-earth orbits are nearly circular and I will consider only orbits whose
altitude is very small compared to the radius of the earth. With each orbit
there is one special speed v for an orbiting satellite where the
centripetal force equals the weight, mv2/R=mg or v=√(gR)
where g is the acceleration due to gravity, R is the radius of
the orbit (approximately Rearth), and m is the mass
of the satellite. If you are going faster or slower than that you will not
be in that circular orbit but some elliptical orbit which happens to cross
the circular orbit. But, let us just suppose that you are going a little
faster than v, say v+u where u<<v; you got there
by briefly firing your rockets out the rear tangent to the orbit. If you do
nothing else, you leave that orbit. However, the force necessary F to
keep you in that orbit would be m(v+u)2/R=F.
But part of F is the weight, so you can write F=mg+f where
f is what your rockets have to do. Therefore f=m(v+u)2/R-mg=m(v2+2vu+u2)/R-mg.
Now, mv2/R=mg from above and you can
neglect u2 because it will be very small compared to 2uv,
so f≈2muv√(g/R); you would have to point your
rockets away from the center of the earth so that this force would be down
but you would keep on that circular orbit going faster than other satellites
in that same orbit.
 QUESTION:
QUESTION:
The speed of sound increases dramatically in water while the speed of light is decreased...why?
 ANSWER:
ANSWER:
The speed of sound v is determined by the bulk
modulus K (related to how hard the material is to compress) and the
density ρ of the material, v=√(K/ρ). For water,
ρ=1000 kg/m3 and K=2.2x109 N/m2;
for air, ρ≈1 kg/m3 and K≈1.4x105 N/m2.
So the prediction by the model equation is that sound is about 4 times
faster in water, a result due mainly to the much larger bulk modulus. Light
always travels faster in a vacuum than through any other medium and you
should think of any material medium as impeding the motion of the waves; for
all waves other than light, the medium supports the wave. To light, air is
extremely close to being a vacuum but water is considerably more interactive
with the light slowing it down.
 QUESTION:
QUESTION:
For a statement to be a law it must be based on observations and
experiments. Newton, certainly didn't perform experiments to verify his universal law of gravitation.
Was it correct then to state it as a law?
 ANSWER:
ANSWER:
Newton may not have done the experiments, but his law was
the result of experiments done by others. Most important were
Kepler's three laws which were empirical summaries of a large body of
data on the motions of the planets. His law of gravitation, F=-MmG/r2,
provided a complete explanation of Kepler's laws. However, since the mass of
the sun was not known, only the product MG could be determined from
the data. A good
measurement of
G was not done until more than 70 years after
Newton's death. Because gravity is such a weak force, this is a very
difficult measurement to make on a laboratory scale.

 QUESTION:
QUESTION:
I have recently begun learning how to play the electric guitar, and the other day my teacher was explaining to me how I can change between different pick ups on my guitar to get a different sound.
I am studying Year 11 Physics and have learnt about the harmonic series and I was wondering why the tone of my guitar changes when I change what pickup I'm using. Are there different harmonics and overtones that are accentuated by different pick ups?
 ANSWER:
ANSWER:
First, you might be interested in a
recent answer. I have shown the first few
possible ways a guitar string can vibrate. In an actual instrument, these
and many more are all happening at once in relative amplitudes determined,
in part, by how the instrument is played. Now, I presume that you have
several pickups placed in different places along the length of the string.
As you can see, the contribution from each overtone depends on where you
look at it and each is unique. One example would be if you put a pickup
right in the center of the string, none of the odd overtones would be
detected. Another example would be if you put the pickup 1/3 the length of
the string, the second, fifth, eighth, eleventh, etc. overtones would
not be detected. (I will let you see if you can figure out how I got that
series!). Basically, your intuition was right, different pickups pick up
different overtones.
 QUESTION:
QUESTION:
This question is in regards to flowing water and buoyancy. Lets say I have two connected reservoirs at different heights, therefore creating a pressure difference and fluid flow between them. There is a pump that refills the higher reservoir so the flow is constant, and there is a section of tubing that is vertical. If I were to put a buoyant object like a balloon in the vertical section of tubing with flow, could I keep it from floating to the top with enough flow? Basically can fluid flow in the opposite direction of the buoyancy force keep it from floating. I feel like it can but I am having trouble understanding why (seems like the only factor is density/displacement, maybe fluid flow increases drag?), just curious because my friend and I got into a random debate about it.
 ANSWER:
ANSWER:
Usually when we
think of buoyant forces we are thinking about fluid statics, all fluid at
rest. Your balloon in the tube will experience a buoyant force up and a
force down from its weight just as it would in a nonmoving fluid. If the
water is moving down, the balloon will also feel a downward force due to the
drag it experiences. What this drag force is will depend on the size of the
balloon, the size of the tube, and the speed of the water. It would be very
complicated to calculate, but I am sure there would be a correct speed for
any geometrical situation where the balloon would remain stationary. If that
is enough, you can stop reading here. If not, here is an example below:
Basically, this is just a terminal velocity
problem. Suppose that we imagine just releasing a spherical balloon with
radius R, volume V=4πR3/3, cross sectional
area A=πR2, and mass m under water. The net
force upward would be F=ρgV-mg=4ρgπR3/3-mg
where ρ=1000 kg/m3 is the density of water and
g=9.8
m/s2 is the acceleration due to gravity. The drag force can be
approximated as f=πv2R2ρCd/2
where the drag coefficient for a sphere is Cd=0.47 and v is the speed of the balloon. So the net force is
Fnet=4ρgπR3/3-mg-πv2R2ρCd/2
and this is zero when v=vt, the terminal velocity, vt=√[(8gR/(3Cd))-2mg/(πR2ρCd))];
the second term in the square root is much smaller than the first because the mass of the
balloon is very small (about 0.04 kg if R=0.1 m and the air is at
atmospheric pressure) compared to the buoyant force. This is how fast a
balloon would rise in still water. So, that would be the speed the water
would have to be moving down for the balloon to stay in place. I did a rough
calculation for R=0.1 m and found vt≈2.4 m/s. These
estimates are all for the size of the pipe much greater than the size of the
balloon. Things get much more complicated if that is not the case, but you
would still be able to use the water flow to keep the balloon in place.
 QUESTION:
QUESTION:
If a dome were on the moon which controlled temperature and
radiation inside. Would an Olympic sized swimming pool be able to be
swum in or would the water become airborne?
 ANSWER:
ANSWER:
There is still gravity on the moon, it is about 1/6 what
it is on earth. So, the water would definitely stay in the pool; a splash
would go much higher and farther than on earth, though. Swimming would be
pretty much the same as on earth, though, because, since you would be
lighter than the water in the same proportion, your buoyancy would be the
same. And, since most of swimming motion is horizontal, motion not affected
by gravity, it would be more or less the same as on earth. If you were to
swim down vertically, the pressure would increase about six times more
slowly since the pressure increase is proportional to the gravity.
 QUESTION:
QUESTION:
Using a hot plate as the sun, I am trying to use a magnifying lens to focus the radiant energy onto a thermometer. I measured the focal point length of the lens using white light at about 22 cm. When I try the experiment, there is no change in the thermometer. Why?
 ANSWER:
ANSWER:
The lens focuses visible light. Your hot
plate is mainly infrared light and the lens is not transparent to infrared
light, it is blocked. So your problem is that the hot plate is a very poor
replica of the sun because the sun is most intense in the visible part of
the spectrum.
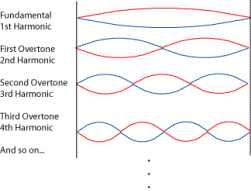
 QUESTION:
QUESTION:
In an acoustic guitar, why does the timbre of a note change depending on where the string is plucked?
Is it to do with different wave lengths?
 ANSWER:
ANSWER:
For nonmusical readers, timbre refers to how a musical
note sounds. How can you tell the difference between a middle C on a piano,
a guitar, and trumpet? They all play the same "fundamental" note which has a
frequency of about 262 cycles per second. But, depending on the design of
the instrument and how it is played, other frequencies called overtones are
also present. It
is the relative mixture of these overtones which determine the timbre of the
instrument. A guitar is a relatively simple instrument in that its overtone
possibilities are all integer multiples of the fundamental. However, the
mixture of overtones may be controlled to some extent by the player by how
he plucks the string. Plucking it at the center, for example, emphasizes all
the even overtones, vibrations which have a maximum at the center of the
string (see the figure to the left). A more lengthy discussion can be found
here.
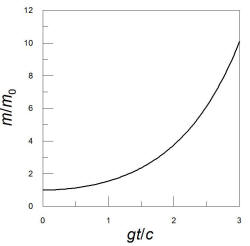
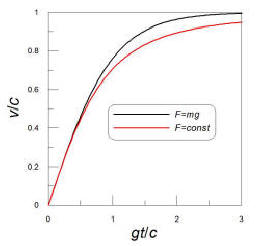
 QUESTION:
QUESTION:
My question deals with the "potential energy"
of a gravitational field, in relativistic terms. As an object falls in a
gravitational field, a tiny bit of its mass gets converted to kinetic
energy, a small reduction in mass. However, according to Special Relativity,
as an object accelerates, gets closer to the speed of light its mass (how it
interacts with spacetime) increases. So, does an object accelerating
(increasing kinetic energy) in a gravitational field lose mass, as a result
of falling in a gravitational field, or gain mass as a result of approaching
the speed of light? OR is there some breakeven point were the reduction of
mass from falling stops, and then mass starts increasing again as a result
of approaching the speed of light. If the mass starts increasing because of
approaching the speed of light, wouldn't the gravitational potential
approach infinite?
 ANSWER:
ANSWER:
You are the same questioner from
earlier similar questions. The reason you do
not want to simply say that there is "a
small reduction in mass" if it is falling is that it is not at rest when you
look at it later. As I explained in the earlier answers, you need to
calculate things relativistically to find out how the mass changes. That is
essentially what the
last link I gave you in my earlier answers does, calculates
β=v/c
as a function of time for a constant force. To know how the mass varies (if
you interpret relativistic momentum that way), just calculate m0/√(1-β2)
where m0 is the rest mass. It occurs to me, though, that
it might be of interest to redo that calculation for a force which is not
constant but which has a value mg=m0g/√(1-β2)
where g is the acceleration due to gravity in whatever strength field
you wish to examine. I will not give all the details here, just the results.
We start by integrating the relativistically correct form of Newton's second
law,
- m0g/√(1-β2)=dp/dt=(d/dt)[m0v/√(1-β2)]
integrated gives
- gt/c=½ln[(1+β)/(1-β)]
solved for β gives
- β=(1-exp(-2gt/c))/(1+exp(-2gt/c));
put this into the mass and get
- m/m0=1/√(1-β2).
These are plotted to the right above.
Note that the
result for a constant force
m0g
is plotted in red for comparison. Potential energy is not a useful concept here. Note that the time to get to
near c, t≈3c/g, is about 2.9 years for
g=9.8 m/s2. At that time the moving mass is about 10 times
greater. A more lengthy discussion of a mass in a uniform gravitational
field (including general relativity) can be seen
here.

 QUESTION:
QUESTION:
Using real-world estimates for the coefficient of friction between his feet and the ground, how fast could the Flash run a quarter-mile? Assume that the limiting factor for his acceleration is the force parallel to the ground that his feet can apply.
 ANSWER:
ANSWER:
Suppose he is running on a dry asphalt road with
rubber-sole shoes. Then the coefficient of static friction is approximately
μ≈0.8. The maximum force of friction on level ground would be
fmax≈μN=μmg≈8m
where m is his mass. So, his acceleration would be a=fmax/m=8
m/s2. A quarter mile is about 400 m, so assuming uniform
acceleration the appropriate kinematic equation would be 400=½at2=4t2,
so t=10 s.
 QUESTION:
QUESTION:
Why is it that hot objects such as lightbulb filaments emit light while cold objects such as ourselves emit no light at all?
 ANSWER:
ANSWER:
Well, let's first define "light" as any electromagnetic
radiation, not just the visible spectrum. All objects radiate light and the
wavelengths they predominantly radiate depends on temperature. A human body
has a temperature around 300 K (800F) and a tungsten filament has
a temperature of around 3000 K (50000F). The picture to the right
shows the radiation for both of these temperatures; also note the visible
spectrum indicated by the colored vertical bands near 0.7 microns. At 3000
K, the radiation is most intense in the region of visible light; at 300 K
there is almost no intensity of visible light and the spectrum is most
intense around 10 microns which is in the "invisible" infrared spectrum.
Night vision goggles are sensitive to infrared radiation and enable you to
see "cold" objects in dark situations.
 QUESTION:
QUESTION:
I have a doubt about static friction and number of wheels.
As for elementary physics principles
1) static friction depends is mass times the coefficient of static friction
2) static friction does not depend on surface static friction is independent by the number of wheels.
... but it is hard to accept to me!
Let's suppose to design a cart to be pushed by a worker. The total weight (cart + content) is about 1000 kg.
The question is: as for the static friction it is better to use 4 or 6 wheels?
 ANSWER:
ANSWER:
If the cart is to be "pushed by a worker" it is not
static but rather kinetic friction which is in play unless all the wheels
are locked. And this is not friction due to the contact between the wheels
and the ground but friction due to the axles rubbing on the wheels. But,
let's talk about friction anyway because you seem to have a serious
misconception. First of all, the friction is proportional to the normal
force which presses the wheel to the road, not the mass. If there were one
wheel, the maximum static frictional force you could get before the cart
started slipping (call that fmax) would be the weight W times the
coefficient of static friction μs (on level ground),
fmax=μsW.
If you had two wheels, each wheel would hold up half the weight so the
maximum static frictional force you could get from each wheel would
be μsW/2; but the total
force is still μsW. Things are more
complicated on a slope, but the conclusion is still that you do not gain an
advantage regarding traction by having more wheels. The reason big trucks,
for example, have many wheels is so that each wheel does not need to support
so much weight, not to get more traction.
 QUESTION:
QUESTION:
I understand that acceleration due to gravity decreases with distance, specifically by the inverse square law. That being said, what is the maximum distance for which one can use 9.81 m/s2 as g for Earth?
 ANSWER:
ANSWER:
That depends entirely on how accurate you want to be,
there is technically no place other than the surface of the earth where this
is the acceleration. Furthermore, the number 9.81 is simply an average
value; it varies over the surface of the earth due to local density
variations, rotation of the earth, influences of the moon's gravity,
altitude variation, etc. You need to ask something like "at what
altitude h from the surface is the value of g changed by X%?"
Then X/100=((1/R)2-(1/(R+h)2))/(1/R)2
where R is the radius of the earth. Provided that h is small
compared to R, you can solve this equation approximately as h≈XR/200.
For example, g will be reduced by 2% when h≈R/100. Another
example: the International Space Station is at an altitude of about 230
miles, about 6% of the earth's radius. Then XISS≈200x0.06≈12%
smaller than 9.81 m/s2.

 QUESTION:
QUESTION:
In a good fireplace the smoke goes up the chimney rather than out into the room even if the fire is not directly beneath the hole.What causes this draft and why is it better the taller chimney?Why is the draft better on a windy day? And why do chimneys puff?
 ANSWER:
ANSWER:
The main reason that the smoke goes up the chimney is
that hot air rises. The hot air from the fireplace fills the chimney and
this rising air results in a lower pressure at the bottom of the chimney. So
all air and smoke at the bottom of the chimney is drawn upward. A taller
chimney is better because there is a larger volume of hot air resulting in a
lower pressure at the bottom; there is a limit, however, determined by
whether air higher up has cooled and by frictional drag considerations over
a longer distance. If a wind blows over the top of the chimney, Bernoulli's
equation tells us that the pressure is lowered there providing an even
greater lift of the air column; from what I have read, though, the hot air
rising is the most important consideration. I do not know what you mean by
"puff".
 QUESTION:
QUESTION:
If I am driving my car with a bowling ball in the trunk, does it take the same energy to accelerate the vehicle to a given speed at a given time if the ball is free to roll around as it would if it were fixed to the vehicle? I assume that the net energy use would be the same in both situations (same total vehicle mass), but the acceleration rates would be different - ie: the fixed ball would result in a constant acceleration to speed, while the rolling ball would result in a non-constant acceleration. If this is true, could I harness the energy of the ball's movement relative to the vehicle (using some sort of linear generator) without causing parasitic energy loss to the vehicle?
 ANSWER:
ANSWER:
As long as the ball and the car end up going the same
speed, the total energy to get them there is the same (neglecting frictional
and air drag forces). If you devise some way to take enegy away from the
ball, that energy ultimately must come from the engine.

 QUESTION:
QUESTION:
What would the yield of a 5000 ton iron slug
accelerated at 95% of C by say a bored Omnipotent be? Would it be enough to
mass scatter a planet?
 ANSWER:
ANSWER:
I get the strangest questions sometimes! So, 5000 metric
tons=5x106 kg. The kinetic energy would be K=E-mc2=mc2[(1/√(1-.952))-1]≈1024
J. The energy U required to totally disassemble a uniform mass M
of radius R is U=3GM2/(5R) where G=6.67x10-11
is the universal gravitational constant. So, taking the earth
as a "typical" planet, U=3∙6.67x10-11∙(6x1024)2/(5∙6.4x106)≈2x1032
J. So your god's slug is far short of supplying enough energy to totally
blast apart the earth.
 QUESTION:
QUESTION:
I am baffled by the fact that if you have a light source and two (or more)
mirrors, you multiply the total amount of light that illuminates a room by
the number of reflecting surfaces. Does this mean that we increase the total
amount of light energy without having to add energy to the light source? Or
does each reflection carry less energy than the incident beam from the
original light source?
 ANSWER:
ANSWER:
Yes, you can brighten a room with mirrors; but there is
no problem of energy conservation because you are simply using light which
would otherwise have been absorbed by the walls. But, not 100% of the light
is reflected because if it were, you could turn off the light and the room
would not go dark; and the room would just get brighter and brighter if you
left the light on. I can do a rough calculation to give you an idea of how
long light would bounce back and forth. Suppose that the mirrors were 99%
reflective (much more than actual mirrors are) and you had two parallel
mirrors separated by a distance of 3 m. Since the speed of light is 3x108
m/s, the time between reflections is 3/3x108=10-8
s. There are therefore 108 reflections per second. At each
reflection the intensity decreases by a factor of 0.99, so after n
reflections the intensity has been reduced by a factor of 0.99n.
Suppose we look at how much light is left after 0.1 ms=10-4 s,
10,000 reflections: 0.9910000≈2x10-44 or 2x10-42
%. I think we can agree that it is almost instantaneously gone!
 QUESTION:
QUESTION:
I was hoping for clarity regarding peak power and its relationship to the amount of joules in a pulse.
Take this simple example. Supposing you have 1 Watt average power, a pulse width of 1 femtosecond, with a repetition of 1 Hz. The average power would be 1 watt, the peak power would be 9.3x1014 watts. My question is, since the average number of joules would be 1J, would there also be peak Joules of 9.3x1014 Joules?
 ANSWER:
ANSWER:
The energy comes in a 1 fs=10-15 s pulse and
there is one of these per second. I do not know where you got 9.3x1014
W unless you know something about the shape of the pulse that I do not. The average power
P over one pulse would be P=1015 W. Since power is energy
per unit time, P=E/t or E=Pt where E is the
energy per pulse, E=1 J. Since there is one pulse per second,
this hangs together because we then have 1 J per second=1 W.
 QUESTION:
QUESTION:
How does 'ball lightning' come about in the atmosphere?
 ANSWER:
ANSWER:
See an earlier answer.
 QUESTION:
QUESTION:
Around 1905 when Lorentz came up with his tranformation equation, it was assumed that c was constant, but was it also assumed that c is the speed limit of the universe?
Why didn't he assume that v could be greater than c in some cases? Why didn't he put a corrective constant next to c in the equation to allow for the case that time might stop BEFORE or After v reaches c?
The reason I'm asking this question is because the Lorentz transformation has time stop exactly when v=c. How did he know that should be the case?
 ANSWER:
ANSWER:
You have your history a little skewed, I think. Lorentz
was working with electromagnetic theory, Maxwell's equations in particular.
The transformation which bears his name was arrived at empirically with no
reference to the speed of light. He noticed that if you took Maxwell's
equations and transformed them into a moving frame of reference that they
took on a different form which was unacceptable because they had internal
inconsistencies which could not be borne out by experiments. He found that
if he used a somewhat different transformation, now called the Lorentz
transformation, the transformed equations were self consistent; he had
stumbled on a truth without understanding what he had. And he certainly did
not consider the speed of light constant because he was one of the foremost
proponents of the luminiferous �ther, the special medium which
supposedly supports light waves. To my mind it is unfortunate that the
transformation is named for him since it was an accidental empirical
discovery, not based on any fundamental physics. Some books try to refer to
the Lorentz-Einstein transformation, but that hasn't really caught on. To
understand why c is a constant and why it has the value it does, go
to my FAQ page; there you can also see earlier questions about why c
is the speed limit. Your question about a "corrective constant" makes no
sense since universal constants by definition do not need correcting. Since
no clock can ever reach c, time never "stops". I doubt that Lorentz
ever thought about time stopping in any context.
 QUESTION:
QUESTION:
What do you think may be some possibilities if heat all of a sudden ceased to exist? Or, is it possible to completely neutralize heat within a contained space?
 ANSWER:
ANSWER:
First of all, read an
earlier answer regarding what heat is. Heat is the transfer of energy,
not the content of energy. Therefore the answer to the first question you ask is that if
there were no transfer of energy, everything would simply stop, I guess.
Regarding your second question, heat flow can be stopped or slowed down for
isolated systems; for example, a thermos bottle.
 QUESTION:
QUESTION:
Perhaps you can help solve a disagreement we have at work. The question being "Does a person's initial velocity during a jump equal their final velocity once the land?" My contention is "no" in that the jumper could theoretically produce any velocity on the way up, but downward would be limited to terminal velocity. Who's right?
 ANSWER:
ANSWER:
Technically, you are correct. If air drag is present,
energy is lost which results in the landing speed being less than the launch
speed. In practice, however, for a person jumping into the air the height
acquired is not high enough for this to be a measurable effect; that is,
this is an example where we can say, as we often do in an elementary physics
course, that air drag is negligible. A typical terminal velocity for a human
is about 120 mph≈54 m/s. If you jumped with this speed you go over 100 m
high, obviously not in the cards. I did a rough estimate assuming the
maximum height you could jump would be about 2 m; if the person drops from 2
m his speed at the ground would be about 6.32 m/s without drag, 6.30 m/s
with drag, a 0.3% difference. For comparison, dropping from 100 m the speeds
would be roughly 44.1 m/s and 37.1 m/s for no drag and drag,
respectively. It is good to be precisely correct as you are, but it is also
good to be able to make reasonable estimates in real-world situations.
 QUESTION:
QUESTION:
It is said that charges are quantised.Also if we bring two identical solid
conducting spheres in contact with each other,their charges are equally
distributed among them. Now suppose if we have a body A with -5e charge and
body B with 0 charge.Now what will be the charge distribution between the
bodies if we bring them in contact and then separate them?Since charges are
quantised,we cannot have 2.5-2.5 distribution.So will it be 3-2 or 2-3
distribution or what?
 ANSWER:
ANSWER:
The rules you learn like the one you quote apply only
when the charge can be thought of as a continuous fluid which can spread
itself out on any surface, no matter how large, and have zero thickness.
Because the electron charge is so small, these rules work very well to
describe electrostatics for normal circumstances. Obviously, a case like you
describe, with 5 excess electrons is in no way like a fluid and I would
guess that anything from 5-0 to 0-5 could be the distribution over a time.
In principle, the 5 electrons would arrange themselves so that each was as
far away from the other 4 as possible, but there would not be a unique such
distribution.
 QUESTION:
QUESTION:
I was looking at a few years old burn scar on my hand today and it got me to wonder what happened on a subatomic level to the electrons and protons of my hand when I received the burn. So could you tell me what happened to the electrons and protons of my hand when I accidentally touched the inside wall of my oven when takibg the food out?
 ANSWER:
ANSWER:
What happens when you cook meat? Chemistry. Adding
sufficient heat will cause some molecules in the meat to break apart and
make new molecules. That same thing happens in your hand when you burn
it�just a lot of chemistry going on. Then later biology takes over and takes
all that burnt flesh and sheds and absorbs the burnt flesh and creates new
molecules specialized to be scar tissue, again basically chemistry. So,
electrons and nuclei of all just move around as molecules are destroyed and
then rebuilt. It is all just a bunch of chemical reactions.

 QUESTION:
QUESTION:
If I consider a
tube both end open and
dip one end in water
(like pipette in chemistry lab)
and close the other by
thumb, water remain
hanged in the tube. If we say it is because
the atmosphere that
pushes up on the water
in the tube is same as
that of remaining air in
tube pushing down on
the water. Won't the
water fall out due to its
own weight as the
upward and downward forces are the same?
 ANSWER:
ANSWER:
As you lift the tube out of the water, the weight of the
water in the tube pulls it down and the volume of air between your thumb and
the top of the water in the tube increases. Because the volume increases,
the pressure decreases so that when the bottom end of the tube is pulled out
of the water the pressure at the top of the column of water is smaller than
atmospheric pressure at the bottom. Therefore, the water column has three
forces on it which are in equilibrium: its weight down, a force down due to
the pressure at the top, and a force up due to the pressure at the bottom.
Your error was in assuming that the pressure at the top of the column is
atmospheric.
 QUESTION:
QUESTION:
If an electron in an atom can only orbit in fixed orbitals at certain frequencies, how does a gas molecule increase its speed when heated. It implies that the gas pressure also would be allowed only at certain energy levels but the pressure seems to increase in a linear way and jump to fixed pressures when the molecule has attained enough energy.
 ANSWER:
ANSWER:
The question is, how can energy be added to a gas? Let's
think about a single molecule in the gas. It has, essentially, two kinds of
energy�internal energy which are allowed states of the molecule and are
quantized, that is restricted to certain discrete values, and the kinetic
energy associated with the molecule's motion as a whole as it hurtles across
the room. This kinetic energy is not quantized. So, when you heat up a gas
you are adding to its kinetic energy for normal temperatures. You have to
get to extremely high temperatures before you start excite atomic states.
You might be interested in why internal states are quantized and kinetic
energy is not. In quantum mechanics, systems which are bound (like electrons
in atoms) are quantized whereas systems which are not bound (like your
freely moving molecule) are not.
 QUESTION:
QUESTION:
When a ball is thrown vertically upwards ignoring air resistance, and another ball is also thrown upwards with air resistance, the time taken is less for the ball with air resistance to reach max height. Why is this "because average acceleration/force is greater"? Wouldn't there be less acceleration/force because the air resistance cancels some out?
 ANSWER:
ANSWER:
The reason is that the ball with air resistance does not
go as high. The force on the ball without resistance is the weight of the
ball pointing in the downward direction; but the downward force is greater
for the ball with air resistance because the drag force is also pointing
down. Therefore the ball with resistance slows down faster so it stops more
quickly. Think of an extreme example: if you throw the ball upwards in honey
which has very great resistance, it stops almost immediately.
 QUESTION:
QUESTION:
If I had a graph of an object's momentum against time, and at t1 momentum is p1 and at t2 momentum is p2. p1 is a positive y value but p2 is negative. Wouldn't the average force be (-p2-p1)/(t2-t1) instead of (p1-p2)/(t2-t1)?
 ANSWER:
ANSWER:
The fact is, both force and momentum are vectors so the
signs of these quantities mean something in one dimension which is evidently
what you are asking about. A one-dimensional vector with a negative value
points in the negative coordinate system direction. Let's take a particular
example of your supposition, p2=-5 kg∙m/s, p1=1
kg∙m/s, and t2-t1=1
s. This means that the particle started out moving in the positive direction
and ended up moving in the negative direction; therefore the average force
causing this must have been pointing in the negative direction, right? The
average force F is defined to be F=(p2-p1)/(t2-t1)=(-5-1)/1=-6
N. Your proposal would give F=(-p2-p1)/(t2-t1)=(5-1)/1=4
N, obviously pointing in the wrong direction. (I have no idea where your
F=(p1-p2)/(t2-t1)
came from; this is also wrong.)
 QUESTION:
QUESTION:
Why do physicists refer to the non-visible portions of the electromagnetic spectrum as "light"? I thought only the visible portion was considered "light".
 ANSWER:
ANSWER:
This is really just semantics and of no real importance.
We often refer to "the speed of light" which is universally understood as
the speed of electromagnetic radiation. I never heard of anyone use the word
light to refer to gamma rays or AM radio waves, for example. If we want to
be very clear, we say "visible light" when referring specifically to the
visible spectrum.
 QUESTION:
QUESTION:
How is it possible to measure the the distance between an electron and a nucleus? I don't mean calculate, but measure. In other words, what is the operational definition of the Bohr radius?
 ANSWER:
ANSWER:
It is not possible to measure the distance because it has no fixed value. All you can do is predict the probability of finding the electron some distance from the nucleus.
There is no operational definition of the Bohr radius, it is just defined
guided by history (Bohr model); you cannot measure it.
 QUESTION:
QUESTION:
Whenever we roll a ball or spin a quarter it will slow down and eventually stop, since energy cannot just dissapear where does it go?
 ANSWER:
ANSWER:
The kinetic energy is being taken away from the ball or
coin by friction. That energy shows up as thermal energy, the
ball/coin-table-air all get a little bit warmer. Also, since you can hear
the ball rolling and the coin spinning, some of the energy must be lost to
sound.
 QUESTION:
QUESTION:
How can the speed of light be constant, when time is not?
In my understanding, the rate at what time passes changes, relative to speed of motion and gravitational forces.
So if the speed of light is 186,000 a second, but a second could flow at different rates, how does this affect the speed of light?
 ANSWER:
ANSWER:
This is a chicken & egg sort of thing. Time not being
"constant", moving clocks running slow, is a result of the fact that the
speed of light is a universal constant. See my earlier discussion of the
light clock which demonstrates this. Not only do clocks run slower, but
lengths get shorter by exactly the same factor. So, if it takes a pulse of
light 1 s to travel between two points A and B separated by 3x108 m for one observer, another observer moving with
respect to the first might observe the same light pulse take 0.5 s to travel
between A and B which are now separated by 1.5x108
m, exactly the same velocity.
 QUESTION:
QUESTION:
If I raise a mass above the earth, you would say that I'm increasing the potential energy by mg x delta(h). So, on a macroscopic scale , if I raise a mass above the earth, doing work, Im actually adding mass to the earth-mass system? and the increase in potential energy (height classically) is actually a small, virtually undetectable increase in mass of the earth/mass system?
 ANSWER:
ANSWER:
Let's look at several ways to understand this situation.
Start with the work-energy theorem which says that Wext=ΔK=½mv22-½mv12,
work done by external agents equals the change in kinetic energy. So, when
you lift it to height h, gravity does Wearth=-mgh
and you do Wearth=mgh units of
work and so kinetic energy is unchanged. This ignores a couple of things,
one being that the earth is not flat and the field is not uniform and
another is that you do work on the earth-mass
system (EMS) thereby increasing the mass of
the EMS. (Since you do work on the EMS, it does the same magnitude of
negative work on you, so your mass decreases by the same amount as the EMS
mass increases; energy is conserved if all forces are internal, that is if
we think of you as part of the earth.) The work done on the mass is
enormously larger than the work done on the earth because both experience
the same force but the earth hardly moves at all while the mass goes
(almost) h, so almost all of the mass increase will be in the mass,
not the earth.
To get an idea of the magnitudes of these
effects, I will do a specific example, m=1 kg, h=1 m, Rearth=6.4x106
m, Mearth=6x1024 kg.
- Work done on m is mgh≈10 J.
- Increase in mass of m is mgh/c2=10/9x1016
≈10-14
kg.
- Earth will move only about 10-23 m, work you did on it will
be only about 10-22 J, mass increase about 10-37
kg.
- I estimate that g will be
smaller by about 3x10-5 m/s2 at 1 m above the
surface, a very small difference. But, it is huge compared to the mass
increase. The effect on g is a 3x10-4 % effect and
the mass increase is a 10-12 % effect.
Note that I have not said anything at all
about potential energy yet. I have always thought, at an elementary physics
level, of potential energy as just a clever bookkeeping device to
automatically keep track of work done by a force which is always there,
gravity in this case. To illustrate,
Wext=ΔK=Wgravity+Wyou,
so ΔK-Wgravity=Wyou so we define
the potential energy difference to be ΔU≡-Wgravity and,
voilá, ΔE≡ΔK+ΔU=Wext
where external work now excludes work done by any force for which we
have introduced a potential energy function; we have simply internalized the
work done by a force always there. This has no effect on my discussion of
mass changes above.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
So, when the mass falls back down thru the distance, the very small change in mass we had on the way up gets converted into Kinetic energy.
now, lets do work in the horizontal plane, so gravity is not a factor. I have a mass, I perform some work on it (adding energy) now energy has mass, but at very very low speeds, compared to light, nature allows MOST of this work supplied to go into a velocity increase, with a very small amount (undetectable amount) to go into mass increase. As such, at low speeds, almost all of the energy supplied (work done) shows up as a velocity increase. Now, at very high speeds approaching light speed, nature in order to not exceed the speed of light, takes most of the supplied energy (work done) and puts it into a mass increase, with very little going into a velocity increase. Is this a correct picture I have of this?
 ANSWER:
ANSWER:
You have it about right.
There are some subtleties, though: if you are going to talk about mixtures
of kinetic and mass energies and introduce particles with large speeds, you
are going to have to start doing things relativistically. I have
emphasized before that you have to be careful about what you call mass.
My own preference is to work only with rest mass which I usually denote as
m. In your earlier question, all particles which we were looking at
were at rest, so when I talked about increase in mass, that was increase in
rest mass. If the object is moving, what do we mean by mass? In spite of
what many text books say, I do not say that mass increases with velocity but
rather that linear momentum has been
redefined in such a way that it is no longer simply mass times velocity.
Now, the energy E of a particle with rest mass m and speed v is
E=√(m2c4+p2c2)
where p is the linear momentum defined as p≡mv/√[1-(v2/c2)].
Now, you will note, if the particle is at rest,
E=mc2 and p=0,
and as long as v<<c,
p≈mv. Also note that kinetic energy is
no longer ½mv2,
rather it is that amount of energy which is not rest mass energy, K=E-mc2;
you can easily show that if v<<c,
K≈½mv2.
For example, v=0.8c=2.4x108 m/s, m=1
ng=10-12 kg:
- p=10-12∙2.4x108/0.6=4x10-4
kg∙m/s, wheras mv=2.4x10-4 kg∙m/s;
- pc=1.2x105 J;
- mc2=9x105 J;
- E=9.08x105 J;
- K=8x103 J, whereas ½mv2=2.9x104
J.
 YET
ANOTHER FOLLOWUP QUESTION:
YET
ANOTHER FOLLOWUP QUESTION:
I just wanted to add that in my previous question, concerning mass changes with increasing velocity, what I'm calling "mass increase"is not a " physical structure" change of an object. I view this increase of mass with velocity as a " change in how the object interacts with space time.
Therefore, I believe that the gamma correction at large velocities is how the object is changing how it interacts with space time.
I think that some people believe this "mass increase" with velocity is an actual accumulation of matter or a physical enlargement of the object. I hope my thinking is correct on this?
 ANSWER:
ANSWER:
Y
ou
are essentially correct. If you want to interpret the new definition of
momentum as meaning that the mass m' of a particle with rest mass m and moving with speed
v is m'=m/√[1-(v2/c2)],
that is fine; with this interpretation you are saying that the momentum is
still mass times velocity but that the mass depends on velocity. But m'
should be thought of as the inertia of the particle and not some measure of
"the amount of stuff" as you suggest. The faster something goes, the harder
it becomes to make it go faster (which means that its inertia is increasing)
until eventually you run against the wall that v must always be less than
c. You may be interested in a
previous answer regarding the kinematics of a particle which experiences
a constant force.
 QUESTION:
QUESTION:
Generally, we are trying to determine how much electricity will be generated by falling water . With that in mind, an engineering group has proposed a project whereby they place one of their machines inside a tube. We have all of the electrical equations worked out from the movement of the blades inside the machine -- the question for the Physicist is this: what is the speed of the water if it falls 5M or 10M or 20M? If the diameter of the pipe is an important variable, the answer is that we can make the mouth of the pipe as wide as we want: 5M, 10M, 20M etc. Bottom line, we want to achieve a water speed of at least 6 meters/second.
 ANSWER:
ANSWER:
You have not given me any details about the source of
this water. This sounds like a classic Bernoulli's equation problem in
elementary physics where you have a deep reservoir and there is a hole at a
depth h in the dam; what is the speed with which the water squirts
out? This hole could be your pipe and the cross section of the pipe does not
matter as long as its diameter is small compared to h. Bernoulli's
equation states that �ρv2+ρgy+P=constant
where ρ is
the density of the fluid, P is the pressure, v is the speed of
the fluid, y is the vertical position, and g=9.8 m/s2≈10
m/s2 is the acceleration due to gravity. In your case, I would
choose y=0 at the bottom of the dam where your pipe is, so y=h at the surface; the velocity at the surface of the lake is
approximately zero and the velocity in the pipe is v; the pressure at
the top and the bottom is the same, atmospheric pressure PA.
So, Bernoulli's equation is �ρv2+ρg∙0+PA=�ρ∙02+ρgh+PA
or, �ρv2=ρgh, or v=√(2gh).
Interestingly, this is exactly the speed the water would have if you just
dropped it off the top of the dam. For example, at a depth of 5 m the speed
should be about 10 m/s before you put your machine in it.
Bernoulli's equation is, essentially, just
conservation of energy for an ideal fluid; water is not an ideal
fluid, but close enough for this to be a pretty good approximation. However,
you will be asking this moving fluid to do work on your generator which will
take energy away and slow the water down. So, maybe it is useful to
calculate the energy which this moving water has. The quantities in the
equation are energy per unit volume of the water, so E=
ρghV where E is the energy
contained by a volume V of the water. The power P (not to be
confused with pressure), is the rate at which the moving water is delivering
energy, P=dE/dt=ρgh(dV
/dt).
If the cross section of your pipe is A, then
dV/dt=Av
so P=ρghAv.
Here is an example: taking h=5 m with
v=10 m/s as above, using ρ=1000 kg/m3, and assuming a
pipe with a diameter of A=1 m2, P=5x105
W=500 kW. You could not get any more power than that from this water.
 QUESTION:
QUESTION:
In Galiean Relativity, there is no such thing as absolute velocity, as all velocities are relative. However, there is such a thing as absolute acceleration in Galiean Relativity.
In Special Relativity, there is no such thing as absolute velocity, however there is also no such thing as absolute acceleration (unlike Galiean Relativity). Isn't the connection/correction to acceleration the Lorentz Transforms Gamma correction, G=1/square root 1-v/c^2?
 ANSWER:
ANSWER:
The Lorentz transformation for acceleration is very
complicated and I will not write it because it really has very little
interest or applicability in the theory of special relativity. As you note,
all Galilean observers will measure exactly the same acceleration. The
reason that this is so important is that Newton's second law, if written as
F=ma, on which so much of classical mechanics hinges,
is true only if all observers measure the same acceleration because surely
all observers will agree on the force applied. Interestingly, Newton did not
write his second law in this form but rather in the form F=dp/dt
where p is linear momentum. You can learn more about
relativistic momentum here and
here. Also
of interest here is the motion of a particle which experiences a
constant force; the acceleration cannot be constant because the particle
cannot go faster than c.
 QUESTION:
QUESTION:
Does Newton's third law apply only to contact forces or to non-contact forces (e.g. gravity, electrostatic force)? Our teacher says that it applies when the bodies come in contact with each other, but I think it should be applicable to both. Which is the case?
 ANSWER:
ANSWER:
Well, it depends on how you state the third law. If you
state it as "if particle 1 exerts a force on particle 2, particle 2 exerts
an equal and opposite force on particle 1", then there are certain cases
where this law does not apply: see an example for electromagnetism in an
earlier answer. However, when
fields are present, Newton's laws are much more subtly stated because the
fields themselves contain energy and momentum. You can read a more detailed
discussion, concerning linear momentum conservation which crucially depends
on Newton's third law, in another
earlier answer.
 QUESTION::
QUESTION::
My question is concerning the energy required to pry apart (binding energy) of molecules ( not nuclear). Such as the burning of hydrocarbon fuels. When you do work against gravity, the work (energy) you put in goes into potential energy above the earth. When you pry apart the molecules, you are doing work against the attractive forces holding the molecule together( binding energy)Does that work appear as potential energy (distance) between the molecules ( if the forces remain attractive) OR does the attractive force between the molecules change from attractive to repulsive or vanish with distance? If the forces remain attractive then the work supplied should become potential energy between the molecules. If the forces vanish, or become repulsive, the work (energy) supplied, prying them apart, should manifest as a small increase in mass of the molecules forced apart. I'm not sure how the forces between bound molecules behave with distance as you separate them.
 ANSWER:
ANSWER:
Molecules are held together by electromagnetic forces, so
it is useful to get an order-of-magnitude idea of the binding energy
compared to mass energies. Consider a hydrogen atom with an electron and a
proton bound together by their electric attraction. The energy necessary to
move the electron very far away is 13.6 eV. The rest-mass energy (mc2)
of a hydrogen atom is about 1 GeV. Therefore, since you have added energy by
ionizing the atom, the atom is lighter by about 100x13.6/109 %≈10-6
%. Any molecular binding energy will be of the same
order-of-magnitude. The energy we get from chemistry comes from mass and it
is extremely inefficient. So, although E=mc2 is at the
heart of things, you usually do not have to worry about mass changes in
molecular chemistry because they are so tiny. To do detailed calculations of
chemical reactions usually requires that you do things quantum mechanically
which requires a potential energy function. These calculations can be very
complex and approximate models are used to simulate the potential energies
of the molecular systems. Once you get beyond the simplest atoms and
molecules, the calculations can only be done numerically and approximately
on computers. An example of a potential energy function, the Morse
potential, for a diatomic molecule is shown in the figure to the left. The
form of this potential is VMorse=De[1-exp(-(r-re))]2;
note that, for one of the atoms in the molecule, the force (slope of the
potential energy function) is repulsive for r<re and
attractive for r>re. This is expected since the molecule
has a nonzero size because of repulsion but is bound because of attraction.
A first approximation often used for bound molecules is a harmonic
oscillator potential (masses attached to a spring).
 QUESTION:
QUESTION:
Suppose an ice cube is suspended in a gravity free region (having room temperature). Now as the ice melts,what shape will the whole system(including melted water) will attend and why? What shape will the solid ice have(i.e will it maintain its cubical shape as it melts)?
 ANSWER:
ANSWER:
First, think about an ice cube sitting on a table. Why
does it melt? Because heat flows through the surface to the small volume of
ice right below the surface causing that small volume to melt when
sufficient heat has been added. But, a small volume near the edge of the
cube has a larger area and a small volume near a corner has a larger area
yet. This is illustrated in the figure to the left: each little cube on the
surface of the big cube has a volume V and faces with areas A.
As you can see, the cube on the face of the big cube has an area A through which heat can flow, one on the edge has an area 2A, and one
in the corner has an area 3A. Therefore, the cube will melt fastest
on the corners, next fastest on the edge away from the corner, and slowest
elsewhere. That is why a cube gets more rounded as it melts. I cannot think
why this would be any different in a zero-gravity situation except that the
water would not flow away. So, you would have a layer of water around the
still unmelted ice but, eventually, when there was enough water, you would
have the unmelted ice inside a sphere of water.
 QUESTION:
QUESTION:
If I observe an object which is in relative motion it will have increased mass and due to length contraction an increased mass density. So can it become a potential "relativistic" black hole?
 ANSWER:
ANSWER:
No. In the frame of reference of the object, everything
is perfectly normal. Besides, a black hole is a singularity, infinite
density and zero size, so the object would have to be going the speed of
light which is not possible.
 QUESTION:
QUESTION:
The speed of a mass thrown from a moving object is effected + or - by the speed of the thrower. Not so with the speed of light. If light speed was limited by some unknown phenomena, that would cause questions in one area - but, with a source moving opposite to the direction of the light, the speed is still the same. Light is not affected + or - by the movement of the source. It cannot travel faster, nor can it travel slower based on external forces, though it can be vector shifted by gravity and the medium thru which it passes. Why? Unless we can find a reason, say in quantum mechanics, like the metaphysical identity of an electron, these known truths appear to contradict the laws of cause and effect.
 ANSWER:
ANSWER:
The speed of light in vacuum, as you note, is constant
regardless of the motion of the source or of the observer. Strange, I know,
but you seem to think that the reason for this is unknown. Indeed, it is
fully understood why the speed of light in a vacuum is a universal constant;
see earlier answers.

 QUESTION:
QUESTION:
I was watching Babylon 5 and in there there was a description of an Earth Alliance space ship weapon. The weapon was a gun that has two very conductive parts on both sides and a conductive armature in the middle and electricity somehow launches the projectile. The gun is 60 meters long, has two barrels with each capable of firing two shots per second simultaneously. The projectile is 930 kg in mass (1.7 m long 20 cm in diameter) to a velocity of 41.5 km/s. The barrel of this electric gun is 60 meters long. Is this kind of gun physically possible to build?
 ANSWER:
ANSWER:
I always like to look first at the energetics when
answering questions like this. Assuming that the acceleration of the
projectile is uniform, I find that the time it would take to traverse the
barrel is 0.029 s and the average acceleration is 1.4x106 m/s2.
Thus, the average force on the projectile would be F=ma=1.4x106x930=1.3x109
N=280,000,000 lb. I do not think you could have a projectile which would not
be destroyed by such a force. But, suppose the projectile could withstand
this force; the energy which you would have to give it would be E=�mv2=8x1011
J. Delivering this energy in 0.029 s would require a power input of P=8x1011/0.029=2.8x1013
W=28 TW; for comparison, the current total power output for the entire earth
is about 15 TW. Or, if you think of the energy being stored between shots,
and there are four shots per second, P=8x1011/0.25=3.2x1012
=3200 GW; the largest power plant currently on earth is about 6 GW. And,
this power source needs to be on a ship? I do not think this gun is very
practicable!
You might be
interested in similar earlier
questions I have answered.
 QUESTION:
QUESTION:
Something
ridiculous I thought of, if the Moon suddenly stopped moving and began to
fall toward the Earth, how long would it take to impact? I'm stumped as to
how to calculate this, as the force on the Moon gradually increases as it
falls, and the Moon also pulls the Earth toward it, and the radius of each
object would have to be included.
 ANSWER:
ANSWER:
I guess I am going to have to put
questions like this one on the
FAQ page. You should read the details of these
earlier questions since I do
not want to go over all the details again. It is tedious and uninstructive
to try to do this kind of problem precisely. I, being a great advocate of
"back of the envelope" estimates, use Kepler's laws to solve this kind of
problem; I have found that a very excellent approximation to fall time can
be found this way. I note that the mass of the moon is only about 1% of the
mass of the earth, the period of the moon is about 28 days, and the moon's
orbit is very nearly circular. The trick here is to use Kepler's third law
and recognize that a vertical fall is equivalent to the very special orbit
of a straight line which is an ellipse of semimajor axis half the length of
the line. Kepler's third law tells us that (T2/T1)2=(R2/R1)3
where Ti is the period of orbit i and Ri
is the semimajor axis of orbit i. Now, T1=28 and R2=R1/2
and so T2=T1/√8=9.9 days. But this is
the time for this very eccentric orbit to complete a complete orbit, go back
out to where it was dropped from; so, the time we want is half that time,
4.9 days.
But this is not what you
really wanted since I have treated the earth and the moon as point masses.
What you really want is when the two point masses are separated by a
distance of the sum of the earth and moon radii, 6.4x106+1.7x104≈6.4x106
m. To see how much error this causes, I can use the equation for the
velocity v at the position r=6.4x106 m if dropped
from r=Rmoon-orbit=3.85x108 m which I derived
in one
of the earlier answers: v=√[2GM(1/6.4x106-1/3.85x108)]=1.1x104
m/s. It would continue speeding up if the collision did not happen, but even
if it went with constant speed the time required would be about t=R/v=6.4x106/1.1x104=580
s=9.6 min. This is extremely small compared to the 4.9 day total time, so,
to at least two significant figures, 4.9 days is the answer to your
question.
An important part of doing physics, or any
science, is knowing when to eliminate things which are of negligible
importance!
 QUESTION:
QUESTION:
If our solar system was formed from a cloud of dust, created by numerous super nova explosions, where we get various elements, and the sun is comprised of the greater part of this cloud, how is it that the sun is comprised of hydrogen burning to make helium? How did the sun separate all the other elements?
 ANSWER:
ANSWER:
Again, I am not an astronomer/astrophysicist. However, I
was just reading in the April 2014 Scientific American an article
about stars early in the universe. When the universe was young, it was
composed almost entirely of hydrogen with only a tiny amount of helium and
lithium. When stars form, they contract gravitationally and heat up as they
do so. But, heating up, the pressure increases and keeps the star from
collapsing further until it can shed some of the heat so that it can
continue contracting. Eventually, a core dense and hot enough forms where
the fusion can ignite. It turns out that hydrogen is not very good at
getting rid of the heat and so more and more hydrogen accumulates;
eventually ignition occurs but the typical early star, because of the
inabilty of hydrogen to cool, is hugely bigger than the sun, anywhere from
100 to 1,000,000 solar masses. These giant stars now eventually die after
burning much hydrogen and creating lots of heavier elements up to iron; they
explode in supernovae and fall back into black holes, scattering the heavy
elements (including heavier than iron made in the supernovae) into space.
Now, to answer your question, the sun has lots of the heavier elements in
it, just a smaller fraction than the planets. It turns out that these
heavier elements are much more effective in cooling the protostar as it is
forming which allows much smaller stars like the sun to form.
 QUESTION:
QUESTION:
Would it be possible to suspend an electron via electrostatic levitation in
a uniform magnetic field? And if the voltage was decreased enough so that
the electrostatic force on the electron was lower than the force due to the
electron's weight would the electron then experience a 'fall' due to
gravity?
I'm asking this because I'm wondering if placing a positron in a uniform
magnetic field (in a vacuum) and lowering the voltage to a very small value
so that the electrostatic force is lower than the weight would cause a
positron to also experience a 'fall'. And if it did experience a fall it
could be ascertained whether it would fall upwards or downwards.
I'm 17 years old and in the UK about to study physics at university in september and was just curious about this since one of our topics this year was electrical phenomena and we talked about millikan's oil drop experiment which featured a similar sort of suspension when the electrostatic force and force due to gravity were balanced.
It's a thought I had when wondering if antimatter
was affected by gravity the same way matter is.
 ANSWER:
ANSWER:
It is always nice to see young folks asking interesting
questions. First, I need to correct one thing: everywhere you refer to a
"magnetic field" you should say "electric field"; a magnetic field exerts no
force on a charge at rest which is what you want to observe, � la
Millikan. Now, it is known to extraordinary precision that the inertial mass
of a positron is equal to the inertial mass of an electron. By inertial mass
I mean the ratio of the force you apply to it divided by its acceleration,
in other words its resistance to being accelerated. (A more correct way,
relativistically, to say this would be that they have equal momenta for
equal speeds.) I believe it is true that nobody has ever "weighed" a
positron by measuring the force it experiences in a gravitational field.
But, if the gravitational mass were different from the inertial mass, this
would fly in the face of the theory of general relativity. But, let's talk
about the feasibility of your experiment. The mass of an electron is about
10-30 kg so its weight would be about 10-29 N (taking
g≈10 m/s2). The electron charge is about 1.6x10-19
C and so the electric field required to levitate an electron would be 10-29/1.6x10-19≈6x10-11
V/m. Suppose we use a parallel plate capacitor to create this field. The
charge density σ on a plate with field E is about σ=ε0E≈10-11x6x10-11=6x10-22
C/m2 which would correspond to an electron density on the plates
of about 6x10-22/1.6x10-19≈0.004
electrons/m2! This would correspond to about one electron for
every 250 square meters! That would not give a very uniform field would it?
There is no such thing as a uniform surface charge density because charges
in nature do not comprise a continuous fluid; so really tiny uniform fields
are not possible. I did all that just for the fun of it, but there is an
even more serious consideration�the earth itself has an electric field near
the surface of typically 100 V/m pointing down, so an electron would be
repelled upward. To do your experiment you would have to get rid of that
field and I do not believe that it would be possible to be assured that you
could make the residual field much less than your
6x10-11 V/m. Back to the drawing board! Keep asking those hard
and interesting questions, though, and good luck with your university
studies.
 ADDED
NOTE:
ADDED
NOTE:
A
recent article discusses a new proposal to compare matter and antimatter
weights.
 QUESTION:
QUESTION:
If there is a planet on the opposite side of the sun, directly across from the earth,
rotating at the exact speed as the earth, could it go unnoticed?
 ANSWER:
ANSWER:
Certainly not in this day and age when we have space
probes all over the solar system. It seems that in earlier times such a
planet would be detectable only by its gravitational effects on other
bodies, for example comets or asteroids, which have orbits which cross
earth's orbit.
 QUESTION:
QUESTION:
I'm a Science Olympiad coach trying to optimize the performance of our "Scrambler", a car which must be accelerated by only a falling mass.
Most competitors simply tie a weight to a string and route that string over a set of pulleys (using no mechanical advantage to convert the vertical falling acceleration horizontal.
�Read a whole lot more!
 ANSWER:
ANSWER:
Sorry, but if you read site groundrules you will see that "concise, well-focused questions" are required.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I was hoping you'd like the challenge of a motion/force problem that must span across several formula -- PE, KE, PEspring, velocity solved by
acceleration and distance only, etc. Something to sink your teeth into...
 ANSWER:
ANSWER:
It is really not that interesting to work the whole thing
out, but on second thought it is interesting to talk qualitatively and
generally about the questioner's proposal; so I will do that. I will
summarize the situation since I am sure none of you loyal readers will want
to read the whole original question. By using a falling mass M
attached to a car of mass m, it is wished to maximize the speed v
of the car for M having fallen through some some distance H.
The car moves only horizontally. The simplest thing to do is to have the two
simply attached by a string over a pulley. Then, using energy conservation,
0=�(M+m)v2-MgH or v=√(2MgH/(M+m)).
What the questioner proposes is to hold the car at rest and insert a rubber
band in the string so that the falling weight stretches the rubber band
which has been carefully chosen to be just right that, when M has
fallen H, it has just come to rest and is held there. Now,
presumably, the rubber band has a potential energy of MgH. If the car
is now released, the rubber band will presumably contract back to its
original length giving its potential energy to the car, MgH=�mv2
or v=√(2MgH/m), a considerable improvement. My
suggestion would be to use a spring rather than a rubber band since a rubber
band has much more damping (energy loss due to internal friction) and
hysteresis (will not return to its original length). Since the rules fix M and
H, one obviously wants m to be as small as possible.
 QUESTION:
QUESTION:
What is the moon's orbit around the earth? I was wondering if you could send me pictures and diagrams or whatever you could about the orbit.
 ANSWER:
ANSWER:
I am not sure what you want. The moon has a nearly circular
orbit of radius about 385,000 km. It takes about 28 days to go around earth
once (which is how it came to be that a month was a standard time
measurement). The same side of the moon always faces earth which means it
also takes about 28 days to rotate once on its axis. The picture above is
drawn to scale. For more detailed information, see the
Wikepedia entry.
 QUESTION:
QUESTION:
Why is charge a scalor quantity if different charges are given positive and negative signs and also if the flow of current which is mainly due to the flow of electrons but has direction,by convention,same as that of protons??
 ANSWER:
ANSWER:
What makes you think that a scalar quantity cannot have a
sign? How about Celsius temperature, -400C or +200C?
How about time, -5 s is 5 seconds before t=0. The fact that electrons
have negative charge is just an accident of history. All important aspects
of electromagnetism would be just the same if you called the electron charge
positive. The reason that current is defined to flow in the direction of
positive charges has to do with the definition of
current density
which is a vector quantity.
 QUESTION:
QUESTION:
What is the size of an image as a function of its constant velocity ? i.e. what is the percentage increase of the image of a square travelling at 1 m/s towards a fixed camera? Is there some equation to calculate this?
 ANSWER:
ANSWER:
Since you do not give any details about the camera, I assume
it has a fixed focal length f. I will call the size of the object L, the size of the image
h, and the distance from the camera to
the object R. You wish to relate the rate of change of h, u=dh/dt,
to the rate of change of R, dR/dt=-v where v is
the speed the object is approaching the camera; note that if the
object is approaching the camera, R is decreasing, i.e. dR/dt<0.
(If you do not know calculus, you will not understand my work here but you
will end up with a formula for the rate at which h changes.) Because
of the geometry of the situation (shown to the left) we can write L/R=h/f
or h=Lf/R. Differentiating, dh/dt=-Lf(dR/dt)/R2
or u=Lfv/R2. This is the rate at which h
is changing. Suppose that f=5 cm=0.05 m, v=1 m/s, L=10
cm=0.1 m, and R=2 m; then h=0.05x0.1/2=0.0025 m=2.5 mm and
the image is growing at the rate of u=1.25 mm/s. After 1 s, the
object has moved 1 m and so now h=0.05x0.1/1=0.005 m=5 mm and is now
increasing at the rate of 5 mm/s. So, you see, the rate the image increases
in size depends not only on v but also on how far away the object is
(R) and how far the image is from the lens (f). If you need to
know what h is as a function of t, you need to also know where
the object was at some earlier time which I will call t=0; then R0=R(t=0)
and so R(t)=R0-vt. Finally, we can
write h(t)=Lf/R(t)=Lf/(R0-vt).
For the example above and choosing R0=2 m, the graph on
the right shows the image size as the object approaches the camera; note
that both the size and the rate of growth approach infinity as R
approaches zero (t approaches 2 s).
 QUESTION:
QUESTION:
If you have a glass tube with an object inside and the tube contains a vacum, why can you see the object in the tube and why doesnt the inside of the tube go dark like outer space. What are the photons interacting with?
 ANSWER:
ANSWER:
The air has almost no effect on light�light entering your tube behaves almost as if the
air
were not there. In space, the vacuum itself is not dark and transmits light
just fine. What is dark is the "sky" because although the air on earth has
almost no effect on light, a very tiny fraction of light does scatter
from the air and, because the sun is so intense, the whole sky is brightened
by our seeing this scattered light.
 QUESTION:
QUESTION:
If an infinite number of bullets were fired from a gun at a solid target, would one of those bullets "pass through" without making a hole/dent ?
 ANSWER:
ANSWER:
No. See earlier answers.
 QUESTION:
QUESTION:
If the speed of light is constant for all observers, then why does
the Doppler effect for light take place?
 ANSWER:
ANSWER:
Because light frequency is a clock subject to time dilation
and light wavelength is a distance subject to length contraction. Because of
the constancy of the speed of light, however, the Doppler effect for light
is independent of whether it is the source or the observer who is moving,
unlike the situation for sound.
 QUESTION:
QUESTION:
How far apart must electrons be from one and other before they stop exchanging photons or does that only happen when atoms are sharing electrons in the same valence shell (assuming my question has a basis - I have no formal physics background, just what I read in places like this great site and others!)
 ANSWER:
ANSWER:
Photon exchange should not be taken too literally. It is a
cartoon attempting to demonstrate how the field quanta (photons) convey the
force (electromagnetism). And, it has nothing to do with whether or not the
electrons are sharaing some shell. Any time charges are in an electric field
there are virtural photons. Regarding the distance, there is theoretically
no cutoff distance where "they stop exchanging photons" because the electric
field from a single electron extends all the way to infinity.
 QUESTION:
QUESTION:
Without having wings, how does a helicopter turn in air?
 ANSWER:
ANSWER:
First of all, a helicopter does have wings. The rotor is
shaped like a wing and moves through the air by spinning thereby creating
lift. Imagine the path of the overhead rotor as a disk. The rotor is
connected to a plate called the swashplate (the thing between the rotor and
the fuselage in the picture) which can be tilted relative to the main shaft
to the motor and which causes the disk of the rotor to tilt relative to the
horizontal plane. Tilt it forward and the helicopter goes forward, to the
right and it goes right, etc. The swashplate is controlled by a
joystick in the cockpit called the cyclic. The tail rotor is also used in
turns, controlling yaw (rotation about a vertical axis); yaw is controlled
with foot pedals.
 QUESTION:
QUESTION:
Suppose there are 2 mirrors facing each other and I light a laser perpendicularly to one of the mirror and instantly remove my hand . Will the light beam continue striking from one mirror to the other?
 ANSWER:
ANSWER:
See an earlier
answer.
 QUESTION:
QUESTION:
How do we convert electron volts to wavelength or vice versa, example: the wavelength of 50 KeV x-rays?
 ANSWER:
ANSWER:
The energy of a photon is E=hν=hc/λ where
h=4.14x10-15
eV∙s is Planck's constant, c=3x108 m/s is the speed of
light, ν is the frequency, and λ is the wavelength. So,
E=1.24x10-6/λ
eV or λ=1.24x10-6/E
m.
 QUESTION:
QUESTION:
Does acceleration have momentum?
In other words if you fire a rifle, does the highest velocity of the bullet occur as it exits the barrel or does the acceleration increase after it leaves the barrel?
 ANSWER:
ANSWER:
In terms of physics nomenclature, your first question has no
meaning. But your second question seems to clarify what you mean: if
something has an acceleration does it keep accelerating even if there are no
forces on it? The answer is an unequivocal no. The only thing which causes
acceleration is force and when the bullet exits the barrel of the gun the
force which was accelerating it disappears. If there were no new forces on
it, it would continue with the same velocity it had when it exited. There
are, however, two important forces on the bullet when it is outside the
gun�gravity and air drag. Gravity causes it to accelerate toward the ground
and air drag causes it to slow down.
 QUESTION:
QUESTION:
I would like to know if amplitude is a scalar or vector quantity. The definition of amplitude of a wave is written as the maximum displacement of a point from the rest position but why doesn't the calculated amplitude have a plus or minus sign before the magnitude? If we have a type of sound waves that have a maximum negative displacement of 5 cm and a positive displacement of 3 cm, what is then the amplitude of the wave?
 ANSWER:
ANSWER:
Amplitude is a positive-definite scalar and is defined as "the maximum displacement or distance moved by a point on a vibrating body or wave measured from its equilibrium position".
In the example you cite, amplitude is 5 cm. For a traveling wave, there is
one amplitude of the wave; for a standing wave, each point in the wave has a
different amplitude ranging from zero (nodes) to some maximum value
(antinodes). A closely related quantity is the root mean square (RMS)
displacement where displacement is squared, averaged over one cycle, and
then the square root taken.
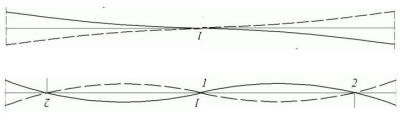
 QUESTION:
QUESTION:
We have a metal ruler 1 yard in length. If held in exact balance center then "pinged" it causes vibrations. nothing new there BUT at exact equal distances to either side there is a point at which it appears that the vibrations stop (a calm spot) for about 1 inch then the vibrations start again and continue to the end. We've tested and the vibrations don't stop, they are just a much smaller wave length. What is is this "calm spot" phenomenon? What causes it? Does it happen with earthquakes too?
Really geeked out about this! Way cool!
 ANSWER:
ANSWER:


You are exciting standing waves when you "ping" the stick. These are waves
which bounce back and forth from the ends of the stick and, for special
wavelengths, are just right to to resonate like a guitar string or an organ
pipe. The various wavelengths for which resonance occurs are called the
modes of oscillation. For a stick clamped at the middle, the lowest mode,
called the fundamental, has approximately 1/4 of a wavelength on either side
of the center as shown by the upper part of the figure above. A point with
zero amplitude, the center for the fundamental, is called a node and points
with maximum amplitude, the ends for the fundamental, are called antinodes.
What you are seeing is the next mode, called the first overtone, which has
approximately 3/4 of a wavelength on either side; this mode has three nodes
and four antinodes. To the right are animations for a stick clamped
at the end but they are exactly what your stick is doing on one half. Here
the nodes are near the darkest blue. Earthquakes are traveling waves and
therefore do not have nodes.
 QUESTION:
QUESTION:
I have points A, B, and C which are moving in 3 dimensional space. If I use point A as a frame of reference, I know the direction and velocity of points B and C. If my points are moving arbitrarily close to the speed of light, what equations would I use to calculate the relative velocity of C from B's frame of reference, and the difference in clock speeds between those two points?
I understand how I would do this if the speeds were nowhere near the speed of light, but things get a tad complicated after accounting for relativity.
 ANSWER:
ANSWER:
I have previously dealt with relativistic
velocity addition if the velocities of B and C are colinear: in your
notation, VCB=(VCA+VAB)/(1+(VCAVAB/c2));
read VXY as velocity of X relative to Y. This may be
generalized
to noncolinear motion as VCB=(VCA+V‖AB+γCA-1V┴AB)/(1+(VCA∙VAB/c2))
where V‖AB
and V┴AB
are the components of VAB
parallel and perpendicular, respectively, to VCA and
γCA-1=√[1-VCA2/c2].
Note that if the speeds are small compared to c,
VCA∙VAB/c2≈0
and γCA-1≈1
so VCB≈(VCA+V‖AB+V┴AB)=(VCA+VAB).
The reason that the transformations are different for parallel and
perpendicular motions is that there is length contraction for the parallel
motion but not for the perpendicular motion. (Note:
VXY=-VYX.)
 QUESTION:
QUESTION:
I've been reading about rotational space habitats for a while now and haven't found an answer to this question by googling. So how would a space habitat be rotated? By cogs? By propulsion systems?
 ANSWER:
ANSWER:
If you want to read more about the details of such habitats,
see my earlier answers (1 and
2). In answer to your question,
you would need thrusters to get the ring spinning and then to occasionally
correct minor changes, but once it was spinning, it would continue to spin
just the same forever if there were no external torques on it as would be
the case in empty space.
 QUESTION:
QUESTION:
The moon's gravity is one sixth that of the earth. Thus if you kicked a box with a force of 60 N across a frictionless floor on earth, the box would travel the same distance in 1 second as when the same box was placed on a frictionless floor on the moon and kicked with a force of 10 N. Am I wrong?
 ANSWER:
ANSWER:
You are wrong on both your conclusion and on your
"�kicked�with a force of�" premise. First the premise: you need to go the
FAQ and read the link
from the question about how much force does it take to make something move
with some speed. Just knowing the force you cannot know the resulting speed;
you need either how long the force was applied or over what distance it was
applied. Now, your question implies that you think it will be easier to get
the box on the moon moving with the same speed as a box on earth with that
speed. But, in fact, the box has the same mass on both the earth and moon
and you are not lifting it against gravity, so it is equally easy to move a
box horizontally on earth or the moon. It is six time harder to lift a box
on earth as on the moon. If there were friction, however, it would be harder
to move the box on earth than on the moon because the frictional force on
the moon would be six times smaller.
 QUESTION:
QUESTION:
I know that neutrons is placed in a wax container to contain the neutrons, but why is this an effective way to contain the neutrons. I want to take in account the linear momentum and the energy, but I'm not sure how to begin or where to do the research?
 ANSWER:
ANSWER:
The wax does not "contain" the neutrons. Most neutron sources
yield fast neutrons and most uses for neutrons need slow (called "thermal")
neutrons. Thus the source is encased in a block of paraffin which serves as
moderator, i.e. the paraffin slows the neutrons down. The reason that
paraffin is good is that it is a hydrocarbon and has lots of hydrogen in it.
Hydrogen is good to slow down neutrons because the best way to slow down a
fast moving object is to collide it with an object at rest which has about
the same mass (think of a head-on collision of two billiard balls); hydrogen
has about the same mass as a neutron.

 QUESTION:
QUESTION:
How do CDs create rainbows when we shine white light on them?
 ANSWER:
ANSWER:
Because they have many closely spaced lines which act like a
diffraction
grating.
 QUESTION:
QUESTION:
What is the difference in time dependent and time independent Schr�dinger equations?
 ANSWER:
ANSWER:
The solution of the time-dependent equation is the wave
function as a function of space and time; the solution to the
time-independent equation is the wave function as a function of only space.

 QUESTION:
QUESTION:
why does a piece of chalk produce hideous squeal if you hold it incorrectly?
 ANSWER:
ANSWER:
It is caused by friction. If the conditions are right
(holding it incorrectly), the chalk will stick, slip, stick, slip, stick,
slip� very rapidly, hundreds or thousands of times per second. This results
in a resonant response of the chalk itself, vibrating loudly. The same
slip-stick friction is responsible for how a violin bow works.
 QUESTION:
QUESTION:
How can the speed of light be the fastest thing in the universe if it is a relative measurement? I mean that if you had two light particles going in opposite directions, wouldn't one go twice the speed of light relative to the other?
 ANSWER:
ANSWER:
See my FAQ page. It is
a relative measurement, but your idea of the relative velocities is
incorrect at large speeds. You want to use
v'=(u+v),
but the correct expression is
v'=(u+v)/[1+(uv/c2)]
where
c
is the speed of light; notice that if
u
and
v
are both small compared to
c,
your expectation is very nearly correct. For your particular example,
u=v=c
and so
v'=(c+c)/[1+(c∙c/c2)]=c.
You can also find other answers about light speed, the maximum velocity
possible, etc. on the FAQ page.
 QUESTION:
QUESTION:
I read
a question on your site about using magnets to propell a spacecraft. I want to expand on that question. How would it affect the movement of the ship if we'd replace the bar magnets with electric magnets and then make one magnet stronger than another? Shouldn't the direction with weaker magnet start to move since the the weaker magnet can not completely nullify the effects of the stronger magnet?
 ANSWER:
ANSWER:
Newton's third law always applies: if one magnet exerts a
force on the other, the other experiences an equal and opposite force from
the one. All forces interior to the spaceship must add up to zero.
 QUESTION:
QUESTION:
I am confused about 1/2mv^2 and mgh.
If an object is lifted vertically up at a constant speed, the formula is mgh. But wouldn't the object also gain k.e. too due to the constant velocity? So wouldn't the total energy be mgh+1/2mv^2?
 ANSWER:
ANSWER:
If it is still moving when you get to h, then its
energy is indeed mgh+�mv2. In a textbook, we
usually envision the mass being lifted from rest at one location to being at
rest at some higher location. During this process, the total amount of work
you do is mgh and the total amount of work the weight (gravity) did
is -mgh so the total work done is zero and the change in kinetic
energy is thus zero.
 QUESTION:
QUESTION:
If you have two permanent cylindrical magnets (the kind with a hole in the center) and you stack them with poles opposite on a pencil, the top magnet will "float" above the bottom magnet. Energy is being expended to keep the magnet "up" the pencil. Where is the energy coming from? The bottom magnet will be pushing down with an equal but opposite force, but that does not cancel the energy needed to float the top magnet as far as I can see.
 ANSWER:
ANSWER:
I am afraid you do not understand energy. The lower magnet
exerts a force on the upper magnet. The force holds it there in equilibrium,
it does not require energy to hold it there. It is no different from saying
that if one of the magnets were hanging from a string, where does the energy
to hold it there come from? Or, if one of the magnets were sitting on a
table top, where does the energy to hold it there come from?

 QUESTION:
QUESTION:
I read of "gravity assist" swingy-bys of Jupiter to speed a spacecraft up to reach the outer planets. As the spacecraft approaches Jupiter, it speeds up. But it retreats from Jupiter on a symmetric path (a hyperbola I think) and Jupiter will therefore slow the spacecraft down by the same amount on the outbound path. It appears there should be no net increase in speed, just a bending of the spacecraft path. But bending a spacecraft path also takes energy. So Jupiter is providing the energy in some manner though it is unclear to me how.
 ANSWER:
ANSWER:
The trick is that the planet, with much greater mass than the
spacecraft, is moving in its orbit and the boost comes from using the speed
of the planet to speed up the spacecraft. The figure shows the idealized
one-dimensional interaction with planet; because the mass of the spacecraft
is much less than the mass of the planet, the spacecraft picks up twice the
speed of the planet. For those who have studied elementary physics, this
should look vaguely familiar: a perfectly elastic collision between a BB at
rest and a bowling ball with speed U results in the BB going with
speed 2U and the bowling ball still going U. (Of course, this
is only approximately true if the mass of the BB is much smaller than
that of the bowling ball; the bowling ball will actually lose a very tiny
amount of its original speed.)
 QUESTION:
QUESTION:
The number of known Mars Meteorites on Earth at last count I know of was greater than the number of Lunar meteorites. This is the opposite of what you would expect: The moon is 140 times closer than Mars with a weaker gravitational field to recapture the meteorites and no atmosphere to slow material blasted off the planet. The number of Lunar meteorites on Earth should be hundreds of times greater than Mars Meteorites.
 ANSWER:
ANSWER:
As always, a disclaimer that I am not an astronomer. The
origins of either lunar or Martian meteorites are major asteroid or comet
impacts; after impact, some of the debris has enough velocity to escape the
gravitational field. First of all, the cross sectional area of the moon is
about 4 times smaller than Mars, so all things being equal, the probability
of a major impact is 4 times greater for Mars. Second, Mars is closer to the
asteroid belt and would therefore, I presume, be more likely to suffer an
asteroid impact. Most major impacts occurred early in the history of the
solar system when embryonic planets were "sweeping up" material in their
orbits and there was a much greater potential of major impacts. These
early meteorites from the moon which landed on earth would have been eroded
away or taken under the crust by tectonic action; those from Mars would have
gone into orbits around the sun and land on the earth over a much longer
period, probably still landing today.
 QUESTION:
QUESTION:
My son and I are trying to build a Foucault pendulum. We have 11' ceilings so we need to dampen ellipsoidal motion and provide a drive mechanism to keep the pendulum moving. I've seen pendulum driver circuits that operate via magnetic induction with relays, transistors, etc. but do not prefer these; it's not clear that the pendulum and Earth are doing the magic, as opposed to the electronics.
I'm thinking of the following design: bend a 20' steel 1" conduit into a circle. Then wrap say 16 gauge bare copper wire evenly and entirely around the doughnut creating a precision ring shaped electromagnet. Then power the ring shaped magnet with a variable DC supply to create the proper pull on, say, a 6lb steel pendulum that swings inside the ring. The idea is to adjust the voltage to give the electromagnet enough pull to keep the pendulum swinging, but not so much that it overcomes the force of gravity pulling the pendulum back to the center, thereby sticking the bob to the electromagnet. That solves the problem of keeping the pendulum moving.
 ANSWER:
ANSWER:
After thinking about this a bit, I believe there are serious
flaws here and your idea will not work. If you put a ferromagnetic material
(e.g., your pendulum bob) in a uniform external magnetic field, that
field will polarize the material and essentially make it look like a bar
magnet with north and south poles. The south pole will feel a force opposite the
direction of the field and the north pole will experience the same magnitude
force in the direction of the field�a bar magnet in a uniform field
experiences zero net force (see left figure above). Admittedly, the field
due to your ring (see figure at the right above) is not uniform but, over
the size of your bob, it is approximately uniform. Forces due to the small
nonuniformity would be mainly in the vertical, not horizontal, direction.
 QUESTION:
QUESTION:
the bond between carbon and oxygen atoms in a carbon dioxide molecule behaves like an elastic spring and vibrates the molecule.why?
 ANSWER:
ANSWER:
It is easier to just talk about a diatomic molecule like O2.
When you understand that you can generalize to any molecule. Think about the
forces between two atoms. If you try to pull it apart, this force tries to
pull it back together or else it would not be a molecule; and, since the
molecule has a size larger than the size on one atom, if you try to push the
atoms together, the force tries to push them back apart. This is exactly the
way a spring works and so a reasonably good model for a molecule is that all
the atoms are attached by tiny springs. Of course, they are not but this
still is a model which can help you understand many molecular properties.
So, one of the ways you can excite (add energy to) a molecule is to get it
vibrating.
 QUESTION:
QUESTION:
why does the ground frost go deeper when the surface begins to thaw?
 ANSWER:
ANSWER:
The way you frame this question is that frost has gone to
certain depth before the thaw and then goes deeper because of the
thaw. In fact, there is what is called a
frost front, the line between frozen and unfrozen soil, which moves
slowly downward if the air temperature is below freezing. When the air
temperature goes above freezing, the top thaws but the frost front
continues moving down for a while because there is still a frozen region
above it which prevents it from getting the information that the air has
warmed. So, the thaw does not cause the frost to deeper, it is just
continuing what it was already doing. Eventually the thawing will reach the
frost front and all the soil will be thawed; in some arctic and antarctic
regions, the thaw will never reach all the way to the frost line and
permafrost results.
 QUESTION:
QUESTION:
If an elementary particle has a mean lifetime of say 1 second and there are 1 trillion particles in the system then about how many particles will be left after say 100 seconds?
 ANSWER:
ANSWER:
See a recent question and then do the
calculation: N=N0exp(-t/τ)=1012exp(-100)=3.7x10-32.
Although there is a nonzero probability (3.7x10-30 %) that there
will be a particle left, for all intents and purposes there are none left.
(Incidentally, there are two meanings of the word "trillion". In the US it
means 1012 but in some countries it means
1018. Look
here for
more detail.)
 QUESTION:
QUESTION:
During a discussion with my 6th grade class about the Law of Inertia and space travel, a student asked: "If a spacecraft leaves a solar system, for example Voyager 1, will its velocity increase due to the lack of gravity from the sun." Fairly certain the answer is no; however, it did spark a rather interesting debate. Can you explain?
 ANSWER:
ANSWER:
Perhaps the key is to note that "leaves the solar system"
does not mean that there is no longer any gravity from the sun.
Rather there is a boundary where the solar wind, particles like protons and
electrons, stops; this is called the heliopause and has been definitely
observed by the Voyager 1 spacecraft as shown in the graph to the right.
This shows the amount of solar wind the Voyager detected as it moved during
the months of 2011-2. In September 2012 it dropped to near zero. This is
where we define the edge of the solar system to be and it is about 50
Astronomical Units (AU) from the sun; the earth is one AU from the sun. But
the gravity from the whole solar system is still present and the craft will
continue slowing down, but ever so slightly since as you get farther away
from a mass the gravity gets weaker. This craft has enough speed that, if it
never encountered any other mass it would keep going forever. I did a rough
calculation and found that the acceleration of Voyager is about a=-0.01
mi/hr2 which means that it loses about 1/100 mph per hour; but
the speed is about 40,000 mph, so I think we could agree that it is moving
with an almost constant speed. As it gets farther away, the acceleration
will get even smaller (physicists call slowing down negative acceleration,
not deceleration). Until it gets close to something else, like some other
star, it will keep going with an almost constant speed. When it does
approach another star it will begin speeding up. Your students should
appreciate that the only thing which can change the speed of something is a
force, a push or a pull.

 QUESTION:
QUESTION:
I am building a cold frame to keep veggies alive in the winter. It will be 3' x 6' with two "doors" (called lights) each 3' x 3' that will be hinged to the frame. The frame probably weighs about 10 - 15 lbs. The doors will be quite lightweight, possibly only 3lbs each. I wanted to use magnets to keep the doors closed at night or when I am not venting the cold frame. We often get very windy days with 40mph wind speeds and gusts to 60 mph. From what I've read, magnets have different "pull force" properties. I'd like a way to figure out what pull force the magnet for each door needs to have to withstand the winds we get. Please don't tell me to just hook the doors closed -- shockingly, it appears magnets are a more cost effective solution.
 ANSWER:
ANSWER:
I must say that I cannot believe that you could not buy a
couple of simple hooks/latches for under $5, but I will do a rough
calculation for you to estimate the force you would need to apply at the
edge of the doors to hold it down in a 60 mph=26.8 m/s wind. When a fluid
moves with some speed v across a surface, the pressure is lower than
if it were not moving; this is how an airplane wing works and why cigarette
smoke is drawn out the cracked window of a car. To estimate the effect,
Bernoulli's equation is used: �ρv2+ρgh+P=constant,
where ρ is the density of the
fluid (ρair≈1 kg/m3), P is the pressure,
g is the acceleration due to gravity, and h is the height
relative to some chosen h=0. For your situation both surfaces are at
essentially the same height so PA=P+�ρv2
where the pressure inside your frame is atmospheric pressure (PA)
and the velocity inside is zero. So, PA-P=ΔP=�ρv2=�∙1∙26.82=359
N/m2=7.5 lb/ft2. This would be the pressure trying to
lift the door. So the total force on each door would be F=AΔP=9∙7.5=67.5
lb where A=3∙3 ft2=9 ft2 is the area of the
door. But, this is not the answer since we want to keep it from swinging
about the hinges, not lifting into the air. So, assuming that the force is
distributed uniformly over the whole area, you may take the whole force to
act in the middle, 1.5 ft from the hinges, so the torque which is exerted is
1.5∙67.5≈100 ft∙lb. But, the weight of the door also exerts a torque, but
opposite the torque due to the wind (the weight tries to hold it down)
-3x1.5=-4.5 ft∙lb. So, the net torque on the door about the hinges is about
95 ft∙lb. To hold the door closed, one needs to exert a torque equal and
opposite to this. To do this, it would be wisest to apply the force at the
edge opposite the hinges to get the maximum torque for the force. The
required force from your magnets would then be F=95/3=32 lb. Note
that this is just an estimate. Fluid dynamics in the real world can be very
complex. Also note that, if my calculations are anywhere close to correct,
you should probably be sure the whole thing is attached to the ground or the
side of your house since the total force on the whole thing would be
67.6+67.5-3-3-15=114 lb, enough to blow the whole thing away in a 60 mph
wind! Also, once the door just barely opens, the wind will get under it and
simply blow it up, Bernoulli no longer makes any difference.
 QUESTION:
QUESTION:
If a particle has a lifetime of say 100 years then what are the chances that that particle will decay in 1 year. How will one go about calculating particle decay probability?
 ANSWER:
ANSWER:
Lifetime has no meaning for a single particle. It is a
statistical concept as I will show. The rate at which a large ensemble of
particles decays is proportional to how many particles there are, dN(t)/dt=t/τ
where N(t) is the number of particles at some time t
and τ is the mean lifetime. The solution of this differential
equation is N(t)=N0exp(-t/τ)
where N0=N(t=0). So, when t=τ,
N=0.37N0, there are 37% of the original particles
left. For your question, you might want to ask what is the situation when t=1 if
N0=1 and τ=100:
N=exp(-0.01)=0.99. If you want to interpret that as a 1% probablility
that the particle has decayed, I guess that that would be ok. But, of
course, there is no such thing as 99% of a particle. Keep in mind, though,
that this is not linear; for example, if t=50=τ/2,
N=exp(-0.5)=0.61, not 0.5.
 QUESTION:
QUESTION:
where does electron go that created by beta emission?
 ANSWER:
ANSWER:
The electron is not "created" in a vacuum, a proton and a
neutrino are also "created" and a neutron "destroyed." The net effect is
that there is still the same amount of charge, zero, after the decay as
there was before. One possibility is that the electron never leaves the
source and, since the atom it left is now positively charged, the electrons
in the source all move around until all the atoms have the correct number of
electrons. Or, if it leaves the source, it will encounter other matter with
which it will interact, lose energy and either find a positive ion somewhere
to join or stick to a neutral atom which becomes a negative ion. Charge can
build up to some limit on anything.

 QUESTION:
QUESTION:
Galileo was punished by the Church for teaching that the sun is stationary and the earth moves around it.His opponents held the view that the earth is stationary and the sun moves around it.If the absolute motion has no meaning, are the two viewpoints not equally correct or equally wrong? i.e, By the concept of relative motion can't we say both?if so, then why do we usually say that earth goes round the sun,and the other way round?
 ANSWER:
ANSWER:
If the sun and earth were both just moving with constant
velocity and not interacting in any way, you would have a point. However,
because of their gravitational interaction and the fact that the mass of the
sun is hugely bigger than the mass of the earth, there is no way you can
sensibly argue that the sun orbits the earth. Each exerts a gravitational
force on the other (equal and opposite) but because the sun is so massive,
the force has almost no effect on it. If the earth were not orbiting but
simply released from rest, it would fall into the sun. There would be no
question which object had the greater acceleration�it would be obvious to
any observer that it was the smaller mass, the larger mass practically
unaffected. So, if any frames are accelerating, they are not equivalent to
those not accelerating. What you call "the
concept of relative motion" applies only to unaccelerated frames.
 QUESTION:
QUESTION:
Two spherical bobs, one metallic and other of glass, of same size are allowed to fall freely from the same height above the ground. Which of the two would reach earlier and why?
 ANSWER:
ANSWER:
Two objects with identical geometries (same size and shape)
experience identical air drag force while moving with a speed v.
While falling, the force has a greater effect on the less massive causing it
to slow down more. Therefore the mass, not whether glass or metal,
determines which gets to the ground first; the winner is whichever has more
mass. You can find links to many old answers about air drag on the
faq page.
 QUESTION:
QUESTION:
Suppose you have radiation detectors fixed on the ground on Earth. Will they detect radiation coming from a charged particle in free fall near them?
The first answer that comes to mind is: Yes, they will detect radiation because the particle is accelerated, and electrodynamics predicts that accelerated charges must radiate in this situation.
According to the Equivalence Principle, this situation is equivalent to detectors fixed on an accelerated rocket with acceleration g moving in the outer space and far away from the influence of other bodies. If the answer to the previous question is yes, then the detectors on the rocket should also detect radiation coming from a charge in free fall as observed by the reference frame of the rocket. But a charge in free fall in this reference frame is at rest in the inertial reference frame fixed with respect to the distant stars, and a charge at rest in an inertial frame should not radiate.
Is it possible that detectors fixed on the rocket detect radiation but detectors at rest in the inertial frame do not? Is radiation something not absolute, but relative to the reference frame?
 ANSWER:
ANSWER:
This is a fascinating question and points to an experiment
which would seemingly violate the equivalence principle. The answer to your
first question is an unequivocal yes, an electric charge accelerating in
free fall in a gravitational field radiates electromagnetic waves, an
electric charge not accelerating does not radiate. But, suppose that you are
falling along with the charge; relative to you the charge is not
accelerating and therefore not radiating. Or, equivalently, suppose that you
are in a spaceship in empty space with your rockets turned on. If you
release an electric charge inside, it will "accelerate" toward the rear of
the ship and therefore radiate because the equivalence principle states that
there is no experiment you can perform which can distinguish between the
accelerating frame and a static gravitational field. However, the charge
will move with constant speed relative to an inertial observer nearby and
therefore not radiate. In both cases we have an electric charge both
radiating and not radiating, a seeming paradox. Although I had not heard of this
paradox before, apparently it has been a topic of many articles. The most recent of
these, by
Almeida and Saa,
has evidently laid the paradox to rest. They demonstrate in this article
that observers for whom the charge is not accelerating "…will not detect any radiation because the radiation field is confined to a spacetime region
beyond a horizon that they cannot access…" and "…the electromagnetic field generated by a uniformly
accelerated charge is observed by a comoving observer as a purely electrostatic field."
Like all "paradoxes" in relativity, there is not really a paradox; rather a
radiation field in one frame may be a static field in another. Basically,
you nailed it when you said "radiation
[is] something not absolute, but relative to the reference frame."
 QUESTION:
QUESTION:
What would happen if a needle that weighed as much as the Earth and everything on it was placed on the surface of the planet? Where would the pin end up? What would be the impact on the Earth? Would the outcome be different if it was set on land or water?
 ANSWER:
ANSWER:
This is a wacky question but I guess I can do a wacky
question now and then. I will take "placed on" as being synonymous with
"suddenly appears at the surface". It will also be easier to think about if
the needle appears at the equator. I will also assume that no matter what
happens, the needle retains its size and shape. If the needle just sat
there, the effect would be that the earth would now rotate not about its
axis but about a parallel axis which is halfway between the center of the
earth and the needle; the length of the day would increase to about 5 times
the current 24 hours. But, it would certainly not stay on the surface of it.
The force which the needle would exert on the surface of the earth would be
about 6x1025 N. But this force is over an area of a needle, very
tiny, so the pressure would be astronomical. This would cut into the earth
and the needle would end up, probably after oscillating back and forth for a
while, at the center of the earth. The length of the day would return to
about 24 hours and everything on the surface would weight twice as much. If
the needle were to appear at a pole, there would be no effect on the length
of the day at all.

 QUESTION:
QUESTION:
If a dogs bark measures approximately 60-80 decibel, how much will it reduce traveling in air (average 20 Celsius) over 500 meter.
Could you please brake down the formula for me so I can calculate other distances.
 ANSWER:
ANSWER:
You should first read an
earlier answer for a detailed
explanation of what a decibel (dB) is. The main reason for loss of sound
intensity I (measured in watts per square meter, W/m2) is
that the sound waves spread as they get farther away so the energy per
second (power) striking your ear gets smaller. The intensity falls off like
1/R2 where R is the distance from the source. You
do not specify the distance from the dog that the 60-80 dB level is
measured, so I will arbitrarily put it at 1 m. Therefore the ratio of
intensities at 500 and 1 m would be I500/I1=1/5002
or I500=4x10-6I1. But,
the catch is that dB is a measure of the level L (a logarithmic
scale), not the intensity. So we need the equations to convert between L
and I. These are L=10∙log10(I/10-12)
and I=10-12∙10(L/10) where I is
in W/m2. So, as an example I will choose L=70 dB, so I1=10-12∙10(70/10)=10-5
W/m2 and I500=4x10-6∙10-5=4x10-11
W/m2. Finally, we find what the dB level of I500
is: L500=10∙log10(4x10-11/10-12)=10∙log10(40)=16
dB. I believe that this will the main source of quieting with distance, not
any absorption of the sound by the air. Wind can also have an effect on the
intensity if it is across the direction the sound travels to reach you. By
the way, when the intensity reaches 10-12 W/m2,
it will be below the "threshold of hearing" and you will no longer hear it;
that corresponds to 0 dB.


 QUESTION:
QUESTION:
My question is that whether gravitational field an be reversed
in Earth`s atmosphere? it would bring revolutionary changes in Aerospace
engineering.
 ANSWER:
ANSWER:
No.
 FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
but space organisations train their astronauts on how to deal in zero gravity in camps. then they have to create artificial zero gravitational field. how is it possible??

 ANSWER:
ANSWER:
You can simulate zero gravity but you certainly do not do it
by reversing the gravitational field. We are stuck with the field we have
and to simulate zero field there are two ways. The first is to put the
astronaut trainee in a free-fall situation. If you are in a freely falling
elevator, for example, it will seem like there is no gravity. The more
practical way to do this is to ride in an airplane which is moving over a
parabolic path it would follow if it were simply a projectile; inside that
airplane it will seem like there is no gravity. The plane which does this is
affectionlately known as the "Vomit Comet". A second way you can simulate
weightlessness is to build a giant tank of water and then the buoyancy will
provide a force opposite to your weight making the net force on you equal to
zero.
Finally, it should be noted that when you are in
orbit you are also not truly "weightless". In orbit you are constantly in
free fall so, although you still have your weight, you are in free fall just
as you were on the Vomit Comet.
 QUESTION:
QUESTION:
If we are given a graph showing pressure versus distance for a sound wave, does a higher pressure amplitude indicates a louder sound produced?
 ANSWER:
ANSWER:
Sound waves are longitudinal waves of pressure as shown in
the animation at the right. You are right that the greater the pressure
difference between the lowest and highest pressures, the louder the sound.
You should not think of the regions of high pressure being the regions of
loudest sound, though. Because the elapsed time between low and high
pressure hitting your ear is so short, your ear/brain averages the square of
deviation of the pressure in the wave from normal atmospheric pressure to
determine loudness. The information from the time difference is also
processed by the brain and interpreted as the frequency or pitch of the
sound.
 QUESTION:
QUESTION:
Let's say that we started mining for metals and such somewhere other than earth. What if any would the effects of large scale increase (and I mean really really big) in planet mass be? Also what would happen to the other planets we were robbing of minerals as their mass decreased?
 ANSWER:
ANSWER:
As long as the mass of the orbiting body is much less than
the mass of the orbited body, the orbital motion is independent of the mass
of the orbiting body. So, the length of the year would be unchanged.
However, increasing the mass and radius of the planet would increase its
moment of inertia, so its rotational speed would decrease and the day would
get longer. Keep in mind, though, that a huge amount of stuff would have to
be added for any real difference to occur.
 QUESTION:
QUESTION:
In case of string, when only a pulse is sent then why do the particles vibrate just above the mean position and not below the mean position?
Please answer in a way that i could understand. If your answer include some mathematics esp the calculus please simplify so that i could understand
 ANSWER:
ANSWER:
There is an equation, called the wave equation, which to a
fair approximation applies to waves on a string. One of the properties of
this equation is that the wave retains its shape as it propogates. Hence, if
you start with a pulse above the string, it will remain that way.

 QUESTION:
QUESTION:
I am trying to determine the buoyancy of a 10 kg polyethylene tray (density = 0.95 g/cm3=950
kg/m3) that is used in lobster pounds to hold lobsters. The tray holds 60 kg of lobster, and fills up with water up to the lid (which floats at the top of the water). The volume of the tray is 0.1223 m3. The lobsters are held in seawater (density = 1026 kg/m3). So, my question is how much air is required to be placed in cavities in the lid to keep the tray floating at the top of the water?
 ANSWER:
ANSWER:
I will take the "volume of the tray" to be the inside volume,
that is the volume occupied by lobsters and water. The density of a lobster
is sure to vary from animal to animal, but it certainly must be larger than
the water since the creatures dwell on the bottom. I actually found a
measurment of a lobster's density to be 1187 kg/m3, so I will use
that as an approximation for all lobsters. So, the volume occupied by 60 kg
of lobsters is Vlobsters=60/1187=0.0505 m3. So,
the volume of water needed to fill up the tray is Vwater=0.1223-0.0505=0.0718
m3; so the mass of the water is Mwater=1026x0.0718=73.7
kg. The volume of the polyethylene is Vpoly=10/950=0.0105 m3.
So, the total mass is 60+10+73.7=143.7 kg and the total volume is
0.1223+0.0105=0.1328 m3. The density of the full tray is then ρ=143.7/0.1328=1082 kg/m3; since this is greater than the
density of the water (1026 kg/m3), it will sink, hence presumably
the point of this question. In order for it to "just" float, volume must be
increased until the density is equal to 1026 kg/m3, i.e.
1026=143.7/V or V=0.1401 m3; so, the volume of the
air should be Vair=0.1401-0.1328=0.0073 m3=7300
cm3. This would be a volume of a cube about 20 cm on a side. I
guess I would increase that by at least 50% as a safety factor. (Note that I
have neglected the density of the air which is about 1 kg/m3.)
 QUESTION:
QUESTION:
What happens to gamma rays when they are blocked by materials like lead, and how come they're not blocked by some other materials?
 ANSWER:
ANSWER:
For all intents and purposes, gamma rays interact only with
electrons in the material. The two most important ways they interact are the
photoelectric effect where the photon gives all its energy to an electron
and Compton scattering where the photon scatters from an electron, giving
some of its energy to the electron. Which of these is more important depends
on photon energy and other factors. But, as you would think, the density of
electrons in the material is very important. To a very rough approximation,
atoms are all about the same size. That means that there are about the same
number of lead atoms in a cubic centimenter of lead as there are aluminum
atoms in a cubic centimeter of aluminum. But every lead atom has 82
electrons whereas every aluminum atom has 13 electrons. There are therefore
roughly 6.3 times more electrons in a cubic centimeter of lead than in a
cubic centimeter of aluminum; therefore lead will be much more effective in
shielding against gamma rays. Regarding "what happens" to the gamma rays,
they disappear completely if photoelectric effect occurs or become gradually
less energetic and changed in direction if Compton scattered.
 QUESTION:
QUESTION:
To tighten the loose head of a hammer, the base of the handle is sometimes struck on a hard surface. Explain the physics behind this maneuver.
 ANSWER:
ANSWER:
This sort of sounds like homework. The physics is inertia.
The head of the hammer is pretty massive and so it has a lot of inertia, it
wants to keep going. When the handle suddenly stops, the inertia of the head
keeps it moving so that it moves down a bit on the handle before stopping,
thereby becoming more tightly bound to the handle.
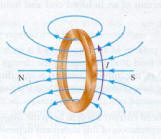
 QUESTION:
QUESTION:
What would happen to a beam of proton particles if the pass through a coil (perpendicularly) imagine a closed circle shaped loop. Currwnt is passing through this coil hencr generating a magnetic field. Will this B field make the particles vibrate? Accelerate them?
 ANSWER:
ANSWER:
I assume that you have the beam of protons very narrow and
moving along the axis of the loop. As you can see from the figure to the
right, the on-axis field is along the axis. Therefore, a beam of protons on
the axis would pass through unaffected because the force on a charged
particle is zero if the velocity and field are parallel. If the proton were
off axis, there would be a small force which, if the proton were in the
plane of the page here, would point either into or out of the page.
 QUESTION:
QUESTION:
Isnt the gravitational pull of an object determined SOLELY on the mass of that object and NOT its size or density? obviously distance from said object plays a role just as size and density affect mass.... however, if what i believe is true, there can be no such thing as black holes, which even today their existence is only theoretical, not proven... anyway my point is this... i believe that if our sun was the size of a basketball but still had the same mass it has today, (giving it almost infinite density)..(what many scientists today consider a 'black hole') but the Earth was still the same 93,000,000 miles from the actual surface as it is today, the orbit of the Earth and the planets would remain, and the sun would not be considered a 'black hole', nor would it behave like one, (sucking in all its orbiting masses, and even light itself).. it would be much smaller, but given the exact same mass and distances surface to surface, little would change as far as orbits go... could this be correct theoretically?
 ANSWER:
ANSWER:
If the object is spherically symmetric and you are totally
outside the mass distribution, then you are right�only the total mass
matters. But, this does not mean that black holes do not exist. It is
dramatic to say that nothing can escape a black hole, not even light, if you
are inside a critical distance called the Schwartzchild radius, but that
does not mean that objects could not orbit the black hole, either inside or
outside that radius. If the sun were a black hole, its Schwartzchild radius
would be
R=2GM/c2=2x6.7x10-11x2x1030/(3x108)2=3,000
m; so all the planets would be outside and would orbit just fine; they could
even be dragged away if you wanted. Only objects inside 3000 m would be
"trapped" but even they could still orbit the black hole. The figure to the
left shows some orbits of stars around the supermassive black hole at the
center of the galaxy which have been observed by astronomers.
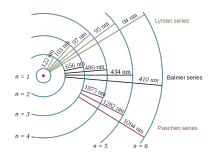
 QUESTION:
QUESTION:
I don't understand the hydrogen spectrum..the theory given in my book says that Balmer series will be observed when electron falls from n=3,4,5......(up to infinity) to n=2 but isn't n=2 for an electron of the hydrogen also an excited state,so it must fall back to its ground state?? Or am i getting something wrong here??
 ANSWER:
ANSWER:
Yes, it must get down to the ground state again once it
reaches n=2. But that is part of a different series, called the Lyman
Series. The radiation from that transtion is called the Lyman alpha line and
is in the ultraviolet region of the spectrum. The rest of the series is
n=3,4,5� going to n=1; all the lines in this series are in the ultraviolet.
Every level has a
series
terminating on it.
 QUESTION:
QUESTION:
if i create vaccum on earth ,like in a spherical shell,if pierced it will suck air around it, its not the case with atmosphere of earth,why it is not that space vaccum suck it?gravity is indeed much stronger near earth and atmosphere much more denser ?
 ANSWER:
ANSWER:
The reason that air does not leak into space is that gravity
holds it to the earth. Think of the air as a collection of molecules all
moving around with different velocities. The velocities are distributed
according to the Maxwell-Boltzmann distribution.
At normal temperatures, most molecules (e.g., O2, N2,
H2O, CO2,�) have almost no molecules have velocities
large enough to escape the
earth's gravitational pull. Lighter molecules, in particular H2
and He, have much higher velocities and do escape into space; you will find
almost no hydrogen or helium in our atmosphere.
 QUESTION:
QUESTION:
With respect to special theory of relativity, light speed c is an invariant, but wouldn't rest mass also be an invariant? If true, why is it not one of the postulates?
Velocity and acceleration are not invariants, but are there other properties that are invariants?
 ANSWER:
ANSWER:
Light speed is not usually referred to as an invariant; it is
simply a universal constant. Furthermore, as I have
stressed before, I see no need to call
the constancy of c a postulate; it is simply a
result of the principle of relativity
which states that the laws of physics be the same in all inertial frames.
Rest mass is the inertia something has in its own rest frame, so of course
it must be a constant. The word invariance usually refers to any
quantity which remains constant when a Lorentz transformation is performed.
For example, the total energy of an isolated particle E=√(m02c4+p2c2)
is an invariant.
 QUESTION:
QUESTION:
I've been trying to calculate how much impact force an object weighing 2,000,000 lbs traveling at 120,000mph will generate. I've run calculation conversions that tells me that the Newtonian Force is a whapping 48665704243.2 but what does that mean? I read about how an 80 pound 1 foot long object traveling at 52,000mph hit the surface of the moon with a force equivalent to 5 Tons of TNT exploding, creating a 65 foot wide crater!
What would my 1,000 Ton 157.64 Mach object do?
 ANSWER:
ANSWER:
For the umpteenth time, you cannot calculate a force by
knowing the mass and velocity of something; see my
FAQ page. What you can do, as your
example does, is calculate the energy which the object carries in. I will
not do what I usually do and convert to SI units since you seem to like
English units. The kinetic energy something has is K=�MV2
where M is the mass and V is the speed. Using your example, KTNT=5 if
K=�∙80∙52,0002=1.1x1011
lb∙mph2, so to convert energy in lb∙mph2, to energy in
tons of TNT you need to multiply by a factor of 5/1.1x1011 lb∙mph2=4.6x10-11.
So,
�∙2x106∙120,0002∙4.6x10-11=6.6x105
tons=0.66 Megatons of TNT. For comparison, the bomb dropped on Nagasaki in
WWII was about 0.02 Megatons.
 QUESTION:
QUESTION:
Why are loops provided for transporting oil/water for longer distances?
 ANSWER:
ANSWER:
When the temperature of the pipe changes it changes length.
In the figure to the left, the pipe will expand if you heat it up and
contract if you cool it down. If it were just a straight pipe, the resulting
forces on the pipe along its length could be large enough to cause it to
buckle and fail. Inserting loops allows the length changes to be taken up by
the size of the loop as shown.
 QUESTION:
QUESTION:
Can u get pure energy? Can you make it visible with power modulation?
 ANSWER:
ANSWER:
Since mass is just another form of energy, everything you can
see or feel is pure energy. Maybe you mean energy without mass? In that
case, the answer would be electromagnetic radiation like light or radio
waves. I have no idea what your second question means.
 QUESTION:
QUESTION:
My question relates to time dilation and the speed of light. When we consider the passage of time, and the speed of an observer or traveler on Earth, how does the speed of our planet around the sun, our arm of the galaxy and the speed of the galaxy itself play into the speed of time for someone on Earth? We talk about a spaceship travelling at a certain speed, but isn't the Earth itself like a spaceship for its inhabitants? And isn't the Earth rotating around the sun at a certain speed, and the spiral arm of our galaxy also rotating at a certain speed? So isn't the Earth also?
 ANSWER:
ANSWER:
Time dilation is meaningful only as a relative thing. One
observer can measure the rate at which the clock of another observer runs.
Relative to a clock on the sun, an earth clock would run slowly. Relative to
the center of the galaxy, an earth clock would run slowly differently.
Relative to a clock on Andromeda galaxy, an earth clock would run slowly
differently. This is the thing about relativity�it is only relative
measurements that mean anything; that's why they call it relativity.
Underlying your question is the misconception that there exists some
absolute rest relative to which all clocks in the universe will run. There
is no such thing as "absolute rest"; any inertial frame may be thought of as
being at rest. Incidentally, for all but the most accurate measurements, the
time dilations I have alluded to are negligibly small because the relative
speeds are small compared to the speed of light.
 QUESTION:
QUESTION:
I don't understand angular momentum but as a first step here is my question. If you hold out weights and turn on a pivot and bring the weights in; are the weights moving at the same velocity and you are spinning faster so that the weights move at the same velocity or are the weights actually moving faster?
 ANSWER:
ANSWER:
The angular momentum L of a mass M a distance
R from the axis around which it is rotating is of L=MVR where
V is its speed. It requires no torque to change
R, so L will stay the same if R is changed because
angular momentum of a system on which there are no torques is constant
(conserved). So, for example, if you change R to �R, V will double. If there were no
person spinning with the weights and no external torques (like friction),
this would be your answer. It is more complicated if you have anything other
than the weights. You probably want to ignore the rest of the answer below,
but I want to do it for completeness.
If you take into account the presence of the
person you need to introduce the moment of inertia I. The angular
momentum now is written as L=Iω where ω is the angular
velocity (in radians per second) of the system. If a point in the system
is a distance R
from the axis of rotation and moving with a speed V, the angular
velocity is ω=V/R. So, comparing with the idealized situation above
you can see that the moment of inertial of a point mass must be Ipoint-mass=MR2.
Now, the man holding the weights has some moment of inertia which I
shall call Iman; I will ignore the contributions from
his arms, so his moment of inertia does not change when he pulls in the
weights. The total angular momentum at the beginning is now L1=(Iman+2MR2)ω1=(Iman+2MR2)V1/R.
So let's again reduce the distance to �R. The new angular
momentum is L2=(Iman+2M(�R)2)ω2=(Iman+�R2)V2/(�R);
this needs to be the same as the original angular momentum, so (Iman+�MR2)V2/(�R)=(Iman+2MR2)V1/R.
Solving, V2=�V1(Iman+2MR2)/(Iman+�MR2).
Note that if Iman=0, you get the same as above, V2=2V1.
If Iman>>2MR2, there will
be negligible change in angular velocity and so V2=�V1
because V=Rω and ω did not change. Finally, there
must be a case where Iman is just right that V2=V1;
that would be if Iman=MR2 and would
correspond to ω2=2ω1.
 QUESTION:
QUESTION:
Where can I find the assumptions for conservation of linear momentum? I'm specifically looking for a source which says that both bodies in a linear momentum problem have to attain a common velocity. The assumption or condition I'm looking for is so basic I can't find it.
 ANSWER:
ANSWER:
You can read my
earlier answer on
momentum conservation. I am afraid I have no idea what you mean by "both
bodies�have to attain a common velocity". In fact, that does not even sound
right to me for a general case.
 QUESTION:
QUESTION:
The question, "Why does water freeze at 32 deg. F?" has been proposed all over the internet. There is not an adequate answer to be found. The answers will describe how it freezes, and what takes place, but never why it freezes. The freezing point of hydrogen is -241.746 degrees celcius and the freezing point of oxygen is -218.79 �C. So why does water freeze at 0 deg C?
 ANSWER:
ANSWER:
Iron freezes around 12000C, mercury at -390C,
etc. The temperature of the phase transition between solid and liquid
depends on the material; it is not a simple thing to predict exactly where
that transition will occur, but it can be done in some cases. It is also
dependent on the pressure. But I am curious: Why do you particularly ask
about water? Why didn't you ask me "why does molybdenum freeze at 26200C?"
This question is "all over the internet"? Guess i missed that.
 QUESTION:
QUESTION:
Hello,when we look at objects with triangular prism instead of of eye glasses we see spectrum or rainbow on objects edges ,why this spectrum is always formed on the edges.
I mean the edges of objects for example chair,wall etc. I mean things i look at through prism instead of eyeglasses.
 ANSWER:
ANSWER:
The ideal situation for seeing a spectrum from a prism is if
you have white light, all coming from the same direction and preferably
through a narrow slit. If you just hold the prism up and look through it,
light of many colors is coming from all directions. When you have an
obstruction, like the edge of a table leg, for example, it lis like "half a
slit" and light coming from the edge is restricted to come mostly from one
direction. If that light has a fairly large fraction of white light, you are
likely to see a rainbow spectrum.
 QUESTION:
QUESTION:
Hi I'm a high school student and having hard time understanding something about electric potential energy. Do electrons moving in a circuit have potential energy because battery has done some work moving them against electric field (from low potential to high potential)? If yes, suppose that I just put the wires around the battery and think about the moment when it took 1 electron from low potential to high potential. That electron now has a potential energy equal to the energy spent when moving the charge from low to high potential. But since a battery doesn't generate electrons (and just providing force to move them) and all other electrons were already there in the copper wire, how did other electrons get their potential energy? The battery hasn't done any work for them (or did it?).
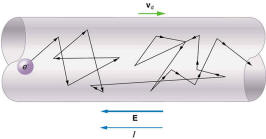
 ANSWER:
ANSWER:
The electric current in a conducting wire is not the best way
to learn about potential energy of charges because it is a rather complicated
process. What happens is that the potential difference across the ends of
the wire cause there to be an electric field inside the wire. Electrons see
this field and therefore each believes that it is in an approximately
uniform field and therefore it accelerates and gains kinetic energy as it
loses potential energy it has by virtue of the field. But what next happens
is that little electron almost immediately encounters an atom in the wire,
collides with it, and loses some or all the kinetic energy it has just
acquired and has to start all over again. So each electron bounces slowly
along the wire, repeatedly gaining and then losing kinetic energy. On
average, there is a net drift of electrons down the wire but it is really
quite slow and we consider the average electron to move with a constant
drift velocity. So any electron, moving from the negative terminal of the
battery to the positive terminal of the battery of potential difference V
moved, on average, with no change of kinetic energy but it has lost eV
Joules of potential energy. Where did that energy go? Put your hand on the
wire and you will see that it has warmed up. If you want a more lucid
example of electrons and potential energy, imagine a uniform electric field
of strength E (like in the gap between plates of a parallel plate
capacitor) with an electron released at some point. Then as the electron
moves, accelerating along the direction opposite the field (because it is a
negative charge), it loses potential energy eEz where z is the
distance it has traveled. After it has gone a distance z, it will have
acquired a kinetic energy �mv2=eEz.
 QUESTION:
QUESTION:
I am reading the ABC of Relativity. This is what I don't understand. If I get on a train in London and travel to Edinborough why is it equally true that Edinborough is travelling towards me? It am the one who initiates the motion. If Edinborough is really moving towards me, how is it also moving towards someone approaching it from the North, at the same time?
 ANSWER:
ANSWER:
The important thing to understand is that there is no test
you can do which determines who is "really" at rest�there is no such thing
as one frame of reference which is absolutely at rest. The way this is
expressed in the theory of special relativity is the laws of physics are
the same in all inertial frames of reference. (An inertial frame is one
which moves with a constant velocity in a straight line, no acceleration
allowed.) This means that there is no experiment you can do inside your
train which will have different result if you were in Edinborough or any other
train. All velocities are relative and it does not matter whom you consider
to be at rest to do physics. You, before you left London, were in the same
frame as Edinborough, and nobody would argue that it was you which caused
the change to a different frame since you were the one who accelerated and
consumed diesel fuel; that does not change the fact that the two frames are,
in all ways, equivalent once you are done accelerating.
By the way, it turns out that the laws of physics
have to be the same in all frames, including accelerating frames. This
is the basis for the theory of general relativity. But, you need not
worry about this is you are just studying special relativity. If you are
interested, see my FAQ page

 QUESTION:
QUESTION:
I was playing a game known as ''Fallout 3'' and in the game there are laser weapons. The laser weapons are powered by a marshmallow sized microfusion cells that are basically miniature nuclear reactors that fuses hydrogen atoms. In the game they produce enough power to turn a 500 kilogram bear into ash in one second. So could a reactor that small produce enough power for the gun and how energy much would a marshmallow sized blob of fused hydrogen produce? A normal microfusion cell in the game has enough energy to fire 24 of these shots. So would it be possible in any way for these laser weapons to be able to be this powerful with an energy source like the microfusion cell?
 ANSWER:
ANSWER:
I have no way to estimate the "power
to turn a 500 kilogram bear into ash in one second". I am sure you realize
that, with today's technology, the possibility of there being such a power
supply is zilch. Let's just do a few estimates to show how hard this is. One
gram of hydrogen fuel (deuterium + tritium), if fully fused into
helium+neutrons, releases something on the order of 300 GJ of energy; so, if
released in 24 one second pulses, each pulse would be about 10 GW. That is
probably way more than your bear burning would need, so let's say 100 MW
would do it; so, we would need about 10-2 g of fuel. I calculate
that to confine that amount of gas in a volume of 10-5 m3
(about 1 in3) would require a pressure of about 5,000,000
atmospheres! That, in itself, should be enough to convince you that this
machine could probably never be possible. If you need more convincing,
consider shielding: 80% of the energy produced is in the kinetic energy of
neutrons. How are you going to harvest that energy in such a small volume
and how are you going to protect yourself from the huge neutron flux? And
surely there needs to be some sort of mechanism to control the process and
convert the energy into usable electrical energy to power the laser; all
that is supposed to fit into 1 in3? This truly is a fantasy game
with no connection to reality!
 QUESTION:
QUESTION:
I read that when no external forces act on a system, the internal forces are paired to balance the momentum.
So if the Universe is considered as such a system where momentum is indeed conserved, every action will have equal and opposite reaction. Is this a sufficient explanation to consider Newton's third law to be a special case of Newton's second law?
 ANSWER:
ANSWER:
Suppose that Newton's third law were not true. For any single
particle in a system of particles Newton's second law would be true but you
would not be able to apply it to the system as a whole. Without Newton's
third law, the total linear momentum of an isolated system of particles
would have no physical significance, it would not be a conserved
quantity. Newton's second law refers only to a single particle and is useful
for systems of particles only because Newton's third law is also true. I
fail to see how that makes the third law a "special case" of the second.
 QUESTION:
QUESTION:
If you were to take a 2 liter bottle of air, down to 10 meters and were to let a slight amount of water into the bottle and then sealed the bottle, what would happen to the bottle when you brought the bottle back to the surface?
 ANSWER:
ANSWER:
It is always hard for a scientist to deal with amounts like
"a slight amount"! If you did not let any air out of the bottle, the
pressure inside would be "a slight amount" higher. If you let in as much
water as would go in without any air escaping, the gauge pressure of the
contained air would be about 1 atmosphere, that is, twice atmospheric
pressure.
 QUESTION:
QUESTION:
If two deuterium atoms collide at an ideal velocity and at an ideal angle, are there conditions where fusion will not occur and some sort of scattering will take place? If so, why or how would scattering occur?
 ANSWER:
ANSWER:
I do not know what you mean by "ideal velocity" or "ideal angle". I can tell you that whenever the two deuterons come close enough together to interact, there are a great many things which can happen, all with specific probabilities ("cross sections" in the usual parlance). Essentially any possible reaction allowed by conservation laws and selection rules can happen. Nearly always, the most likely thing to happen is elastic scattering where two deuterons exit
after the interaction.
 QUESTION:
QUESTION:
Assuming I had a piece of string that was a light year long and I was holding it on 1 end and my friend was 1 light year away holding the other end, with no slack in the string. If I pulled it would they feel the immediately, or no? If not, why?
 ANSWER:
ANSWER:
You would not believe how many times I have gotten variations
of this question. See my faq page for a
similar question. In a nutshell, the information would travel at the speed
of sound in your string so it would take far longer than one year before
your friend felt your tug.
 QUESTION:
QUESTION:
What would happen to a fly while an airplane takes off assuming that the fly was already flying forward while the plane was at rest?
 ANSWER:
ANSWER:
The effect on the air due to the acceleration of the airplane
is quite small; the air pressure at the rear of the plane would
increase very slightly.
In other words, the air stays almost at rest relative to the airplane. Since
the fly flies relative to the air, he is mostly unaffected. He is, however,
accelerating along with the air and the plane, so he would have to fly a
little harder in the forward direction of the plane to continue moving the
same as he was; since a typical acceleration of a commercial jet is about 3
m/s2, this additional forward force would be about 1/3 of his
weight.

 QUESTION:
QUESTION:
why are soap bubbles colorful?what colors are observed when a soap bubble is illuminated by monochromatic light?
 ANSWER:
ANSWER:
The reason is that a soap film has two surfaces from which
reflection of light can occur and they are very close to each other.
Therefore, light of certain colors will interfere constructively while light
of other colors will interfere destructively. A pretty clear explanation as
well as a calculator may be found on the
hyperphysics site. If you illuminate the bubble with monochromatic
light, you will only see that color or no light reflected at all.

 QUESTION:
QUESTION:
I just watched a nature document about the largest snake that ever lived on Earth that was the Titanoboa that could exert a pressure of 400 pounds per square inch and that lived in the water mostly. So my question is that could a Titanoboa destroy a submarine by coiling around it with the pressure of 400 pounds per square inch assuming that the submarine is small enough for the 48 foot snake to coil around it?
 ANSWER:
ANSWER:
The pressure under water increases by about 0.44 psi/ft. To
get to 400 psi, therefore, a submarine must go to a depth of 400/0.44=909
ft. WWII U-boats had collapse depths of 660-920 ft. Modern submarines have
collapse depths of around 2400 ft. So, it depends on the submarine, but most
modern ones could withstand 400 psi. The only proviso is that they are
designed to have the pressure uniformly distributed over the whole surface,
not a narrow band where a snake would squeeze; a very localized pressure
could cause a structural failure at a lower pressure.

 QUESTION:
QUESTION:
I came across
this just now.
It implies a balloon full of air weighs more than the same balloon empty. That doesn't feel right to me as an inflated balloon is surely buoyant by the amount of air it contains. i.e. The extra weight of the air is cancelled out by the buoyancy. The site above is a respected organisation and I would be surprised if is recommending an experiment based on a false assumption. However, I cannot see how the instructions they give could possibly be used to determine the density of air.
 ANSWER:
ANSWER:
You are right, the experiment ignores the buoyant force on
the balloon; if the density of the air in the balloon were identical to the
density of the air outside the balloon, the experiment would fail to find
any weight of air. However, the pressure inside the balloon is greater than
the pressure outside and therefore the density of the air inside is larger
than normal atmospheric density. The experiment then measures the difference
between the mass inside the balloon and the mass of an equal volume of air
at atmospheric pressure. This would still be a reasonable order-of-magnitude
measurement of the density of air. A more accurate experiment would be to
measure the pressure to which the balloon was inflated; with that
information you could do a better measurement of the air density.
 QUESTION:
QUESTION:
I'm interested in why we loose our signal when two walkie talkies get too far apart even there is no obstacle between us. Range of reach of EM waves is infinite, so what's the reason?
 ANSWER:
ANSWER:
You are right, in a vacuum electromagnetic waves last
forever. You are not in a vacuum, but absorption by air is probably very
small for your walkie talkies. The problem is intensity of the waves. If you
are far away compared to the size of the unit, you can say that the signal
spreads out from the sending unit like a sphere. But, there is only a
certain amount of energy in that wave and so the amount of energy
intercepted by the receiving unit gets smaller and smaller the farther away
you go. Eventually, the receiving unit is not sensitive enough to detect the
signal.
 QUESTION:
QUESTION:
What should be the temperature of a gas molecule if it needs to escape out of earth's gravitational pull suppose if we take the case of oxygen at what temperature its average velocity will be enough to escape earth's gravitational pull?
 ANSWER:
ANSWER:
Temperature of a gas is
a statistical quantity, no single gas molecule has a temperature. A gas of a
particular temperature has a distribution of speeds called the
Maxwell-Boltzmann distribution which contains all possible speeds. The
figure to the left shows this distribution for N2 for several
temperatures. The escape velocity from the surface of the earth is about
11,000 m/s, so you can see that a heavy molecule like nitrogen has almost no
molecules going that fast at normal temperatures (300 K), or even if T=1000
K. The picture to the right compares the distribution of speeds for N2
with that for H2, about 14 times lighter. You see that the most
likely speed of H2 is about 4 times faster than N2.
Comparing with the figure to the left, 300 K hydrogen gas would have a most
probable speed of more than 1200 m/s. Although there are still very few with
speeds higher than 11,000 m/s, there are still a few which escape.
Eventually, as the slower molecules speed up to fill in the distribution,
they would essentially all leak out of the atmosphere. That is the reason
why there is almost no hydrogen or helium in the atmosphere. Most hydrogen
on earth is locked up in water and other molecules, but since helium is
inert, the only source of it is from underground, usually as a byproduct of
natural gas wells. The form of the Maxwell-Boltzmann distribution is given
by 4π[m/(2πkT)]3/2v2exp[-mv2/(2kT)].
 QUESTION:
QUESTION:
Assume we're in a very large hollow sphere. (let's say r = 1 light year).
Then we take a very powerful laser with extremely low diffraction and we fire it while effectuating a full rotation with it.
Wouldn't the laser point travel faster than light on the inside surface of the sphere?
Or does it fall as into the immaterial category and is exempted from the rule?
 ANSWER:
ANSWER:
You do not need such an extreme condition to do what you
want. The distance to the moon is about R=3.8x108 m, so if
you swept your laser beam across the surface of the moon the speed of the
spot would be equal to the speed of light c=3x108 m/s if c=Rω
where ω is the angular velocity you are rotating the laser. So,
ω=3x108/3.8x108=0.79 radians/second=450
per second�really easy to do. But that spot is not anything, really, because
the spot a second from now will not be "made of" the same photons that it is
made of right now. The most important thing is that there is no way that
this spot could be made to carry information from one point on its path to
another. And you are right, it has no mass, but even massless light cannot
travel faster than the speed of light.
 QUESTION:
QUESTION:
As a chemistry teacher, I often get questions from students that are best asked of a physicist. Is there a "short" answer to explain the nature of charge? Why are there only two charges? We understand that the assignment of the negative to the electron could be completely arbitrary, but what exactly is a/the "negative charge"?
 ANSWER:
ANSWER:
For every force field in nature there is a corresponding
source of that field: gravitational mass is the source of gravitational
fields, electric charge is the source of electric fields, electric currents
are the source of magnetic fields, quarks are the source of nuclear fields,
etc. Further, if there are two such sources in proximity of each
other, each experiences a force due to the field of the other. We first are
aware of gravitational fields and conclude after some experimentation that
the property something must have to be a source of that field is mass.
Inspired by our success in understanding the gravitational field, we start
looking around for other forces. Combing our hair one morning, we notice a
new kind of force which is obviously not gravity. After some experimentation
we discover that some objects in nature cause electric fields if they have a
property which we call electric charge. So, putting two electric charges
near each other, we find, not unexpectedly, that both experience a force due
to the other. But now there is something different. In gravity, the force
between two masses is always attractive, never repulsive. So mass is
a relatively simple thing because there is only one kind of it. But with
electric charges, sometimes the force is attractive and sometimes repulsive,
so we conclude that there must be two kinds of electric charge which are
most easily distinguished from each other by assigning a sign, + or -. Of
course, further experimentation reveals that opposite charges attract and
like charges repel. Why are there two? Well, just because that is the way
nature is. You might just as well ask why there is only one kind of
gravitational mass. The way that quarks interact with each other is more
complex than just attractive or repulsive and three kinds of the quark
property called "color charge" are required. So the answer to "what exactly
is charge?" is that it is that property which something has which allows it
to both cause and feel an electric field.
-
To see questions and answers from longer ago,
link here.