Older Questions & Answers (#2)

QUESTION:
If Hydrogen is the simplest molecule, was it also the first?

ANSWER:
I presume you mean simplest atom. It is believed that the very early universe was nearly pure hydrogen with a small amount of helium and a smaller yet amount of lithium.

QUESTION:
Free neutrons are unstable. But free nutrons are used in fission reactions, neutron scattering and other processes. How is that possible? Don't the neutrons get converted into protons on the courese of motion?

ANSWER:
The average lifetime of a neutron is about 15 minutes, so their use in the applications you mention is not appreciably affected.

QUESTION:
What is meant by "spin = 1/2" for elctrons? DOes it have anything to do with the spinning of electrons?What is the physical significance of the quantity "spin quantum number"?

ANSWER:
Elementary particles, like classical particles, may have angular momentum. A particle may have orbital angular momentum (like an electron orbiting around the nucleus in an atom or like the earth orbiting the sun) or it may have intrinsic angular momentum (like the earth spinning on its own axis or like the spin angular momentum of the elementary particle). When one goes to the microscopic level of elementary particles, angular momentum is quantized, that is only discrete amounts of angular momentum are allowed; for example, if the angular momentum quantum number of a particle is L, its angular momentum is [h/(2π)]√{L(L+1)} where h is Planck's constant. For a spin � particle, the intrinsic angular momentum quantum number is � and so the particles intrinsic angular momentum is h√3/(4π). Although it is sometimes described as spinning of the particle about its own axis, this is a classical picture which is useful only as a rough means of understanding what spin is. For example, it is impossible to do anything to change the spin of the particle.

QUESTION:
All the diagrams of electromagnetic waves that I have seen in textbooks show the electric and magnetic waves being 180 degrees out of phase. I always thought that the decay of one field caused a buildup of the other and that this would put them 90 degrees out of phase. Are the pictures wrong?

ANSWER:
I do not understand what you mean by phase. In the figure to the right the electric and magnetic fields are in phase; this is the diagram you normally see. The fields are in phase in a vacuum or a nonconducting medium. In a conducting medium they are not in phase, but I do not think that is what you are interested in. This phase relationship is what is predicted by solving Maxwell's equations. What is shown here is what is called a sinesoidal plane-polarized plane wave; the wave fronts are infinite planes, the electric fields are everywhere along one dimension and the magnetic fields are everywhere along one dimension perpendicular to the direction of the electric fields.

QUESTION:
if an object falls towards the earth is because it is atracted by the earht's gravity OR it is because it's following the path of the space curved by the earth's mass and density? Second, is it true that every object in space is affected by the gravity of every object, but in very very very small quantities?

ANSWER:
Our best understanding, based on general relativity, is that it is the latter�space-time is curved. But the consequences of general relativity can be understood as saying that objects with gravitational mass attract each other. Certainly, any object with mass will attract any other.

QUESTION:
I am wondering if my idea is valid, since I have never seen it used before. It seems to me that a rocket launched vertically wastes a great deal of fuel just overcoming inertia AND gravity; and it seems to me that a rocket launched on a horizontal track, like a roller-coaster, which curves upward to the vertical would overcome inertia immediately, and upon leaving the vertical end of the track , would already have attained great speed. Can you tell me the pros and cons of this launch method?

ANSWER:
In the absense of friction it makes no difference how you get from point A to point B because the forces are conservative. You make it sound like you just overcome inertia and then can move on to overcoming gravity. In fact, the rocket has the same inertia regardless of its motion, it is not something you can just get rid of. Using a horizontal track would increase the friction compared to air friction, so it would be less efficient overall. Since the rocket will go very fast, air friction becomes important and so going vertically originally gets you out of the atmosphere as quickly as possible. You can get a little boost by using the rotation of the earth; that is why launch sites are as far south as practicable, for example France launches from French Guiana in South America.

QUESTION:
I have been reading about the new LHC (Large Hadron Collider) that will begin running in Europe soon. I noticed that the LHC will use proton-proton collisions. My question is, why did they decide to use proton-proton collisions instead of proton-antiproton collisions? It seems to me that proton-antiproton collisions would be more advantageous since protons and anitprotons attract and are therefore easier to make collide and protons and antiprotons also produce a disintegration energy when they collide that would add to the attainable energy of the collider.

ANSWER:
The main reason is that it is difficult to get an intense antiproton beam; the antiprotons first have to be made and then bunched together and accelerated. When doing experiments that look for rare events, intensity of the beam is paramount to give one a chance to see the event. Also, your ideas regarding an advantage from the attraction or the "disintegration" is flawed because the kinetic energies (TeV) are so high that the weak coulomb attraction is a negligible component and the mass energy of a proton-antiproton pair (around 2 GeV) is also neglibible.

QUESTION:
My Physics teacher was talking about electrons moving further away from the core when the atom is heated, and then unleasing energy as they move back, when the atom gets colder again... My question is; would it be theoretically possible to utilise that energy to knock a proton out of the core, or make it change polarity and remove itself from the core?

ANSWER:
No, not possible, because the energies associated with atoms is thousands of times smaller than the energies associated with nuclei. Also, the polarity of an electric charge (proton, for example) cannot change.

QUESTION:
My understanding of the nuclear fusion reactions, that are to be the basis of proposed thermonuclear fusion reactors of the future, is that a significant neutron flux is created? How is the structural integrity of the walls of such toroidal reactors going to be maintained, if bombarded by the neutron flux for extended periods?

ANSWER:
You have just hit on one of the many reasons why controlled nuclear fusion has proven so difficult to realize. It still seems decades away from realization. I have heard that it is generally accepted that the containment vessels will have to be changed periodically. That is by far not the most difficult problem faced.

QUESTION:
Is it possible to manipulate magnetic fields? If so, how?

ANSWER:
Of course. If you have a magnet and move it around you are manipulating the magnetic field. If you have an electromagnet you can vary the current to vary (manipulate) the field.

QUESTION:
Yesterday my manager came into work with a cup of water that had frozen in his car overnight. There wasn't a straw, or anything else, in the cup. But the ice, instead of being flat, had what looked like a thin, inch-long shard of ice sticking diagonally out of it. Also, the rest of the surface was kind of wavy, like hardened lava. Why would a frozen cup of water make that strange formation?

ANSWER:
This question has been previously answered.

QUESTION:
It is a simple question, but one that has great meaning for me. I am PhD biologist retired and playing around in a new area. Three bodies in a fixed volume have a fixed total momentum, distributed in the first case evenly, (5, 5, 5), and in the second case unevenly, say, (9, 5, 1). Are the collision rates the same? The answer I would prefer to hear is that the unbalanced case has a lower collision rate, though my instincts from Resnick and Halliday studied long ago fear that the collision rate of the system is just a simple function of the total momentum. Which? Use energy distribution instead of momentum distribution if that makes things easier.

ANSWER:
An important concept here is mean free path (L) which is the average distance a particle travels before encountering a collision. The mean free path depends only on the density of the gas (number of particles per unit volume) and the size of the particles. Average time between collisions will therefore be L/v where v is the average velocity of the particles. (So collision rate would be v/L.) So, in your example, if the masses of the three particles are the same, the average velocities would be the same and the collision rates would be the same. So what you need to look at is not the relative momenta but rather the relative speeds if the masses are unequal.

QUESTION:
If the acceleration of an object toward Earth is independant of it's mass, where is my logic wrong in this hypothetical situation: Suppose there are two objects. One is a golf ball. The other is an object the same size as the golf ball but with significantly larger mass than the earth (say 1,000,000,000 times the gravity of the sun). If you were to time the golf ball falling to earth and the object falling to earth from the same height at the same position in space, it seems they would not fall at the same rate. The object of larger mass would pull the earth instead of the earth pulling it. Since our reference point is the earth, we would see the object "falling" to earth just like the golf ball. But because the gravitational force of the object is many times greater than the gravitational force of the earth, it would have a faster acceleration than "g". So what I'm getting at is that from my limited understanding of this stuff, it seems like mass is negligible only if the mass of the falling object is NOT significantly larger than the object it is falling "towards". But mass is not supposed to matter in a free fall situation. Where am I confusing myself?

ANSWER:
Both objects will have the same acceleration, g. The reason is that each particle experiences a force F proportional to its mass m and each also has an acceleration a=F/m so the acceleration does not depend on the mass. But, Newton's third law says that in each case the earth feels an equal and opposite force due to other object. But the acceleration of the earth toward the golf ball will be unmeasureably small because the force is small and the mass of the earth is big; so the earth will essentially sit still while the ball falls. But the other object has a huge mass and so it exerts a huge force on the earth; so the earth will accelerate "up" with an acceleration much larger than the object accelerates "down", and comes up to meet it. In each case, the object has the same acceleration but the earth has different accelerations. It will therefore take a much longer time for the golf ball to hit the ground than the heavy object even though their accelerations are the same.

QUESTION:
The first question is about pair production. Could you explain it in a very simple (and yet on track) explanation for about the age of 13? The second question is about the law of conservation of mass/matter. While the universe is expanding, does this law apply? Why or why not?

ANSWER:
In future, please abide by the groundrules which stipulate single questions. Second question first: There is no such thing as conservation of mass/matter; in chemistry, it was one of the keystones: combine 16 grams of oxygen with 2 grams of hydrogen and get 18 grams of water. However it turns out that this is not quite true because of E=mc²; some energy is released when you burn hydrogen and this consumes a little mass. However, the chemistry rule is very close to true for chemistry because the energy released is tiny compared to the energy of all the mass. But it is not true for nuclear fusion which is what fuels stars like the sun and these stars get measurably lighter as they age. What is true is conservation of energy for a system (including mass energy).

Your first question answer: Again we are dealing with E=mc²; if we consider a photon (which is a little bundle of light), it has energy. The shorter its wavelength, the more energy it has. For very energetic photons, called gamma-rays, their energy might exceed the mc² energy of an electron plus a positron (the antiparticle of the electron, having the same mass but opposite charge as the electron). If this is the case, then it would not violate energy conservation if the photon suddenly turned into an electron-positron pair. For example, suppose that we have a 1.5 MeV (million electron volts, a unit of energy convenient for this kind of problem, look it up!) Now, the rest mass energy of an electron or positron is about mc²=0.5 MeV, so the photon could turn into a pair and that pair would have, in addition to their mc²energy, about 0.5 MeV of kinetic energy. That is pair production. (By the way, this will not happen spontaneously because a photon is a stable particle; instead you must "tweak" it which is usually done by shooting the photons into a strong electric field like that near the nucleus of an atom.

QUESTION:
im doing a project and im in 7th grade im trying to figure out how to measure the energy someone uses during the hours of a day i just dont know what the formula is to measure how much energy someone uses do you know?

ANSWER:
As a 7th grader, you should learn right now: physics is not about formulas, it is about thinking! Now, the question you ask can never have an answer because it all depends on how energy is used and what energy you want count in the your survey. For example, if I drive a car I would need to know how many miles I drove, what the energy content of a gallon of gasoline was, and how many miles per gallon my car consumed. I will give you one fairly simple example you can use if it is electrical energy you want to calculate. Most devices are rated by specifying their wattage; for example, a 100 watt light bulb comsumes 100 joules per second (a joule is a unit of energy). So, if I burn a 100 watt light bulb for one hour I consume 100 (joules'second) x 3600 seconds =360,000 joules of energy. So your formula is wattage x time (in seconds) = energy (in joules). A more familiar unit of energy is the kilowatt-hour. One kilowatt-hour is the energy consumed in an hour by a 1000 watt device (a kilowatt is 1000 watts) or 3,600,000 joules. If you look on your parents' electric bill you will see that each month you are billed by how many kilowatt-hours your household uses; a kilowatt-hour usually costs between 5 and 10 cents.

QUESTION:
I am a teacher (English teacher, though) writing a program to help visualize relativistic effects for college students (again, in English). I use it to help teach the Modernist worldview. To be accurate, my program needs a very precise definition of the speed of light. Apparently, the last time it was measured was in 1973, when it was 299792.4574 km/sec. My question is: has current technology not allowed us to refine this number to more decimals? I know that the current accepted value is an integer, but that is because in 1983 the uncertainty in the length of the meter was greater than the remaining uncertainty in C, so the meter was based on the then-current definition of C. But this doesn't touch the basic question of whether C has been refined since it was measured in 1973. Can you tell me the best current measurement of c in as many decimal places as possible?

ANSWER:
Well, here is some good news for you: the speed of light is exactly 299,792,458 m/s because the length of one meter is defined (since 1983) to be the distance traveled by light in 1/299,792,458 s.

QUESTION:
why there is no net charge on gaussian surface?

ANSWER:
There is no reason why there should be zero charge on a Gaussian surface. For example, imagine a conducting sphere on which I have placed a certain amount of charge. All the charge resides on the surface. If I say that Gaussian surfaces are concentric spheres, then the charged surface is one of them. Incidentally, any surface you choose to think about is a Gaussian surface as long as it is closed, that is encloses some volume; it just so happens that the most useful Gaussian surfaces are equipotentials.

QUESTION:
What is instantaneous velocity,and can you give me an aexmple using it?

ANSWER:
Average velocity is distance traveled divided by elapsed time. Instantaneous velocity is average velocity evaluated in the limit as the elapsed time becomes zero. This involves differential calculus which is why Newton had to invent calculus to do physics. If you are in a car which is speeding up and you look at the speedometer and it reads 20 mi/hr right now, that is your instantaneous velocity; a little earlier it was less, a little later it will be more. For simplicity I have not worried about the vector nature of velocity; I have assumed that travel is in a straight line like a long straight road. Things get a little more complicated if the path is not straight.

QUESTION:
Is the electromagnetic spectrum truly continuous such that for any two given frequencies, no matter how close together they are, there will always be another frequency between them?

ANSWER:
In principle, the answer to your question is a simple yes. In practice, there is a different answer. No real electromagnetic wave is comprised of a single frequency. Because of the uncertainty principle one needs an infinitely long wave to have a perfectly determined wavelength, therefore frequency. Or one can say that because of the uncertainty principle one needs to observe a wave an infinitely long wave to have a perfectly determined frequency, therefore wavelength. Real waves are of finite extent and therefore contain a distribution of all frequencies. (Determining the details of the distribution is called a Fourier analysis) However, you could have a distribution which peaked at a particular frequency and another which peaked at a frequency arbitrarily close to the first.

QUESTION:
This is somthing that has been getting to me for a while. If a long level is built with a horizontal vial on each end and that level is "calibrated" to work on the earth, will it work if I take it to the moon. Regardless of the moons off-center center of gravity. I Think that the curvature of the surface will be more sever and the distance to the center will be close and this will cause the bubbles to be slightly farther out from the center than they would be on Earth.

ANSWER:
You are correct if the length of the stick is not very small compared to the size of the earth or moon. Otherwise, the effect will be negligibly small.

QUESTION:
i know things don't fall faster at high altitude but it feels like it because there is lower air resistance (right?). In laymans terms, can you please explain to be why air is so thin at high altitudes which makes things appear and feel like the fall faster - Im things particularly in regards to skydivers - they seem to have a little more trouble landing and guiding their chutes in higher altitude.

ANSWER:
When there is less air resistance, things will go faster. If there were no air, the speed would continue getting larger without bound (well, not to the speed of light or higher!) The less air there is the faster an object will go before stopping its acceleration (called the terminal velocity). So, your main premise is wrong�you don't just feel like you go faster, you do go faster. The terminal velocity is also dependent on the mass and, particularly, the geometry; the reason a parachute works is because it has a lower terminal velocity than a rock. Yes, at higher altitudes there is less air resistance so a parachute is less effective; it would be useless if there were no air. The reason the air thins out at higher altitude is as follows. There is a certain amount of air in our atmosphere and, because it has weight, it arranges itself in a layer over the whole surface of the earth. But, the deeper you go into a fluid, the greater the pressure becomes; for example, when you go swimming you can feel the increased pressure by the pain in your eardrums as you go deeper. So, you are at the bottom of an ocean of air. There is a big difference between water and air, though, since air can be compressed and water cannot (for all intents and purposes), so the higher the pressure the denser the air will be. Therefore the air is dense at the bottom and gets less dense as you go up.

QUESTION:
If a spaceship leaves its engine on at full power, will it accelerate forever? (assuming it has endless fuel)

ANSWER:
Well, a really hypothetical question! Yes, it would continue accelerating but as it approached the speed of light there would be less and less velocity increase for each pound of fuel burned because the fastest possible speed is the speed of light. So the energy would keep increasing but the speed would hardly increase at all.

QUESTION:
I thought that magnetic and electric field lines were just convenient representations of how fields varied around charges and magnets, and, in reality the electric field, for example, would vary continously with distance. If this is the case, why do we see lines around bar magnets when sprinkled with ion filings, or lines between parallel plates in castor oil when sprinkled with semolina? What happens between the lines?

ANSWER:
You are right, the lines are just what we draw to convey what the field is like, there aren't really lines. Let me talk just about the iron filings around a magnet since both cases have a similar explanation (polarization). Focus your attention on an iron filing: it becomes polarized, that is it becomes a tiny magnet and it aligns itself with the magnetic field of wherever it is. Now, look at its neighbors: those near its ends will also be polarized but their N(S) pole will be close to the S(N) of our first filing, and they like that; but those alongside it will have their N(S) poles close to the N(S) poles of our first filing and will tend to be pushed away. The net result will be chains of filings separated from each other.

QUESTION:
I am an 8th grade Earth Science Regents student, and I am doing a project on the effect of the density of liquid on magnetism. The problem that I am having is that I cannot calculate the force of the magnet. If the magnet is too strong, it could pull out the object inside the liquid no matter what the density of the liquid is, and no difference will be present between the different types of liquid. How can I calculate the force of the magnet?

ANSWER:
You cannot calculate the magnetic field of a magnet, you have to measure it. It depends on its geometry, how far you are from it, what it is made of, how magnetized it is, etc. Do you have something ferromagnetic inside your liquids? You need to experiment so that your magnet is far enough away so that your sample will not be too strongly attracted but enough to measure. Not to be negative, or anything, but density is not the important quantity here but rather the nature of the liquid itself; is it paramagnetic, ferromagnetic, diamagnetic, etc.? Except for ferromagnetism, magnetic forces are very weak and you are going to have trouble getting reliable results without pretty sensitive equipment.

QUESTION:
When I go into my apartment in the winter, I am full of static electricity. If I touch my metal closet door first, I get an electric shock. I would rate this shock a "2" on a logarithmic 1 to 10 scale. However, if I first turn on the light, I get a shock that I would rate a "3" on the same scale. I do not get shocked by my outlets otherwise and I believe that I have the same static charge for both events. Why is there this difference in the amount of shock? What is the physics that causes additional shock? Is this related to what happens with lightning?

ANSWER:
Electrical codes require that there be a ground for all circuits, and this ground wire is connected to the metal parts of the appliance, lamp, whatever. So, even though one of the two leads to the "guts" of the appliance is also grounded, there is a separate ground for everything which is not electrical. Your door is not necessarily at ground potential. Also, the geometry of what you are touching matters. The door is flat and the lamp presumably has a curved surface; the electric charge on you hand induces a charge on the object you are about to touch which is has a larger charge density on the curved surface resulting in a greater potential difference. By the way, if it is a logarithmic scale, the difference between 2 and 3 is a factor of ten. Is that what you meant? For example, the Richter scale is logarithmic and an earthquake with a Richter scale of 8 is ten times stronger than one with a 7.

QUESTION:
what is a simple formula for calculating the beam divergence of a white light flashlight. Observationally it seems related to the ratio of emitter size to reflector size. E.g, lights with a large reflector diameter (and/or small emitter) seem to produce a more tightly focused beam. A WWII searchlight with a huge reflector produces a very tightly focused beam that converges for a long distance to a "beam waist", then diverges. Details: Assuming a typical white-light focusing flashlight (e.g, Mag-Lite) with a parabolic reflector focused to produce a convergent/divergent beam, how do I calculate the smallest achievable spot size (i.e, smallest beam cross sectional area) at a given distance? How does this vary with reflector diameter, focal length, and emitter source size? I can't just use angular field = arctan (source dia. / focal length), as the beam can be initially convergent then divergent.

ANSWER:
Ah, the neverending quest for simple formulas for a complicated world! There is no such simple formula Unless the source is a point placed exactly at the focus of a parabolic reflector; you must also ignore diffraction and any rays which exit without striking the mirror. In any other case you would have to have to do detailed raytracing which would require knowing the exact geometry of the source and where on the source the focus of the paraboloid was. You would also have to define criteria for quantifying what you mean as beam spot since there will never be a clear-cut spot. This would, of course, be best done with computers. Physics is not formulas!

QUESTION:
I teach AP physics in high school and had a question concerning the electrons of metals. What is the difference between the ionization energy of a metal and its work function ?

ANSWER:
The ionization potential refers to the energy required to remove an electron from an isolated atom. However, the properties of most materials are affected by being in a macroscopic solid, metals in particular. In a metal, the valence electrons are, for all intents and purposes, free to move around, that is they are already detached from the atoms of the metal. To remove an electron from a metal, though, means that you leave behind a positive charge which will attract the electron if you try to remove it, so it takes work to remove an electron from a metal; this is the work function.

QUESTION:
I know what Newton's first law of motion means but could you give me some examples of it? And please make sure they are comprehendible but good enough for a group of teachers.

ANSWER:
They are innumerable! I will give a few:

A spaceship is sent to Mars. Once it has escaped the earth's gravitation and not yet close to Mars, you do not have to keep burning your rockets to keep up your speed; Newton's first law (N1) says that with negligible force an object will move with constant speed in a straight line.
When you stand on a scale there are two forces on you, your own weight (the force the entire earth exerts on you) and the force which the scale exerts on you. Because of N1, the net force on you must be zero (you are at rest), so the force the scale exerts on you must be equal in magnitude to your weight but up. {To carry this a bit further, Newton's third law (N3) says that the force you exert on the scale is equal and opposite the force you exert on the scale and this is the force which the scale registers. A scale does not measure your weight, rather it measures the force you exert down on it which just happens in this case to be numerically the same. If you are in an elevator accelerating upwards, the scale will read something larger than your weight.}
You are pulling a box across a level floor with constant speed. The rope you are pulling on is horizontal. The force with which you must pull is equal in magnitude to the force of friction the floor exerts on the box.

QUESTION:
is it possible to increase gravitational force at a particular place or in a single room?

ANSWER:
The gravitational force depends on the mass located near that place, so all you have to do is put a huge block of lead under the room to increase the gravity. But the gravitational force is so weak that you would be hard pressed to observe any change since the mass of the earth is so large. I estimate roughly that if you put a 10x10x10 m³ block of lead under your floor that the weight of something in the room would increase by about 2x10^-4%!

QUESTION:
A ruler with length lo is at rest in a coordinate frame XY and tilt at an angle 45 degree. I know if paralell the length is not the same for both frame and if perpendicular it has the same length but what about the length of the ruler if it is at 45 degree? And how can i find the angle that i see between the ruler and the direction of motion?

ANSWER:
The component of the ruler along the direction of motion is shortened from (l₀/√2) to (l₀/√2)√[1-(v²/c²)] while the component perpendicular remains (l₀/√2). You should be able to do the trigonometry from here.

QUESTION:
I am a medical imaging student in PA. I asked this question in class and was told not to worry about it, I wouldn't be tested on it, but I would still like to clarify it in my mind. We were studying the difference between characteristic and Bremsstrahlung X-rays. The text stated that characteristic X-rays are dependent on the target material, tungsten for most diagnostic X-ray machines and Mo or a combination of Rh and Mo for mammography. The text further states that a characteristic X-ray occurs when a K-shell electron is knocked out of it's shell and this requires at least 70 KeV of energy and that no characteristic X-rays are produced below 70 KeV and any less would produce only Bremsstrahlung. This makes perfect sense to me when using a W anode, since the binding energy of the K-shell electrons are 69 KeV. However, if the anode is made up of Mo or Rh, the K-shell binding energy is around 20 KeV, so in a mammography unit, wouldn't a 25 KeV setting produce characteristic X-rays? Or would it only produce Bremsstrahlung X-rays?

ANSWER: (Thanks to Dr. Mark Haidekker)
I hope the following answer is helpful to you: You are "�correct in the assumption that characteristic X-rays are produced at lower energies as well. Bremsstrahlung is emitted whenever a high-energy electron changes its momentum. This is when it decelerates and some of its energy is converted to photonic energy. The spectrum of bremsstrahlung is broad. Conversely, when an electron or a X-ray photon of sufficient energy moves an electron out of its shell into a neighboring shell (excitation) or removes it from the atom entirely (ionization), the vacancy gets filled eventually. This process frees energy that gets released as an X-ray photon of exactly the binding energy difference. The emitted spectrum is narrow, and it depends on the atom. Therefore, it is referred to as characteristic X-ray radiation. Characteristic X-ray radiation is not limited to the K shell, nor is it limited to molybdenum or tungsten. If a K-shell vacancy of ionized rhodium is filled, the characteristic X-ray energy will be 23 keV. An electron dropping from the L- to the K-shell of rhodium would emit a 20 keV photon. A copper beam-hardening filter would produce scattered X-rays of about 10 keV. However, any of these low-energy characteristic X-ray energies would be absorbed: Either in the beam hardening filter that can usually be found in front of X-ray tubes, or in the tissue itself as the absorption coefficient of tissue is very high for low X-ray energies. This is why beam-hardening is done in the first place: If low-energy X-rays get absorbed in the patient's body, they don't contribute to image formation, but they do cause ionization in tissue. Therefore, low-energy X-rays get filtered out. In this context, characteristic X-rays from molybdenum or rhodium would not pass the beam-hardening filter, and low-energy emission would not be seen in the spectrum emitted from a typical X-ray unit."

QUESTION:
I left a bowl of water with three hard boiled eggs in the fridge and overnight the top 1/2 in of water froze. The fridge is only around 38 degree F, and nothing else in the fridge froze. Why did the water freeze? My fiancee says it has to do with evaporation because the fridge is really dry.

ANSWER:
I have answered questions before which involve frost forming at temperatures above freezing. These involve both evaporative cooling and radiative cooling, so your fianc�e has a good idea. However, I really find it hard to believe that this could be the answer to your question since a half inch of ice is a whole lot more than a little frost and the temperature is so far above freezing. I suspect a much more mundane reason: I have sometimes found ice on the top of a bottle of milk but only if the bottle has been put in a particular place in my refrigerator. Some locations of the refrigerator are colder than others because of proximity to cooling coils, a duct to the freezer section, or for other reasons having to do with how the refrigerator is engineered. And, the temperature you suspect, 38⁰, may be inaccurate so that the whole refrigerator is set too low making it even more likely that somewhere will be below freezing.

QUESTION:
we are trying to settle a debate at college. our questions regards the 4th dimension and its effects on ourselves in the 3rd dimension. the question is as follows. when you are watching television, are you watching something that happened at a different point in the 4th dimension?

ANSWER:
Normally, the 4^th dimension is regarded as time. Physicists refer to "spacetime" indicating that time is on an equal footing with space in relativity. So any two events which are not simultaneous can be regarded as having happened at different "�point(s) in the 4th dimension". It is interesting that different observers will not agree on what is simultaneous, one of the important findings of special relativity. Another way of saying this is that there is no such thing as absolute time, a god-given clock right for everybody.

QUESTION:
In my physics class, we are only looking at one method of pendulum movement, which is an approximation method depending on the angle being very very small, but i was very curious about what its function would be when the angle is larger. I tried figuring it out myself, but i came across a problem that i have no idea what to do about. Lets say we had a pendulum mass M, Length L, and distance from 0 of X (0 is the middle, where angle Z= 0) If we let it go from a certain point, then the force upon it would be F= Mg[sinZ] (note, using Z instead of theta for the angle made by the pendulum and vertical in radians) Then Ma= Mg[sinZ] So a=g[sinZ] -- a=g[sin{X/L}] (radians arc/length) ANd because in calculus acceleration is the second derivative of the postion function (X) we get X''= g[sin{X/L}] Now here is where i get lost, because i cannot figure out any way to find the function X and i really need help for this... You could rewrite this as f''(x) = sin[f(x)], to make things clearer as g and L are constants, but i have no idea at all how to find the integral to get f[x] (function x) and how to finish this to find a function that gives movement of pendulums.

ANSWER:
Well, you are treading on some pretty difficult stuff here. There are certain aspects of this problem which can be solved using exotic mathematical functions called elliptic integrals, but I suspect you don't want to go there. So let us just say that this problem is one (as are most of nature's real problems) which cannot be solved in closed form in terms of standard mathematical functions. That is, y"+sin(y)=0 is not a differential equation which can be exactly solved. But if we approximate sin(y)≈y, as you have learned in your physics class, it can be solved. But, now you want to do better than that. So you have to use a better approximation for the sine function. Where did the first approximation come from? It came from a series expansion for the sine, sin(y)=y-y³/3!+y⁵/5!-� So, if y is not so small a better approximation would be sin(y)≈y-y³/6. Now you will find that the period is better approximated by T=T₀(1-(A²/8))^-1/2 where T₀ is the period in the small angle approximation and A is the amplitude in radians. For example, if A=90⁰=π/2, T=1.2T₀, about 20% longer. I should warn you that, unless you are pretty handy with differential equations, this is not trivial to deduce. In this day and age, one can solve problems of this type numerically on a computer.

QUESTION:
I try to move a very large boulder here on Earth. If I try to move the same boulder on the moon would it take more force, less force, or would it be the same force. I say same force, because it has the same mass. F = ma. Makes since to me, but my students don't buy it. Any other possible explainations?

ANSWER:
Perhaps what is bothering your students is that friction has not been included in the discussion. In fact, why are you often unable to move a boulder at all here on earth? It is because the static friction between the ground and the boulder is larger than the force you are able to exert. Indeed, the friction is approximately proportional to the normal force which is in turn proportional to the weight, so you might very well be able to move a boulder on the moon which you could not move on earth. However, the lesson you are trying to teach is an important one. So, ask your students to imagine the boulder being placed on a cart on a track with negligible friction on both the earth and the moon; if you exerted a force the same on each, each would move identically. In fact, if you went to the middle of empty space where there was no gravity at all, the boulder would move just the same. This confusion arising from having systems which are complicated by many factors such as omnipresent friction was one of the major impediments to progressing from the Aristotelean view to the Newtonian view of nature.

QUESTION:
What is the relationship between an electromagnetic field or wave and a photon? What is the distinction between a wave and a field?

ANSWER:
Electromagnetic (EM) waves are time varying electric and magnetic fields. An EM wave is normally characterized by a frequency f, a wavelength λ, a speed c, and an amplitude usually specified by specifying the maximum electric field value. It was discovered in the early 20th century that sometimes an EM wave will behave like a stream of particles called photons. (You might want to research the photoelectric effect and Compton scattering to see the historical origins and verifications of this discovery.) This type of duality turns out to be pervasive for all of nature, in particular a thing we have always thought of as a particle (an electron, for example) will behave like a wave if we design an experiment to look for wave properties. It is a true feature of nature and physicists and philosophers refer to it as the wave-particle duality. For EM waves, the amount of energy which a photon has turns out to depend on the frequency of the radiation, E=hf where h is Planck's constant. A photon is a special kind of particle in that it has no mass.

An EM wave is, as I said above, time varying electric and magnetic fields which propogate through empty space (unlike most waves) and has a speed which is independent of the speed of the source or observer, independent of the frequency or wavelength or amplitude of the wave. So all EM waves are fields. However, all fields are not waves. For example, there is an electric field around an electric charge but it is not a wave if the charge is at rest or moving with a constant speed; and, there is a magnetic field around a current carrying wire which is not a wave if the current is steady.

QUESTION:
Some of my friends and I recently moved to St Louis, MO. We have all independently found that twist top bottles, no matter where they are originally from, are somewhat difficult to open. We have been told that the center of the continent and the center of mass of the continent are nearby and that St Louis or the surrounding area used to be a huge exporter of lead. Does any of this explain this weird phenomenon? Do nearby dense areas have an effect on torque? If so, would this translate into the tightening of a twist top bottle over time?

ANSWER:
You're jokiing, right?

QUESTION:
My students hear all the time that there is ZERO G. I tell them that astronauts are free falling, like someone jumping out of an airplane. But I hear professionals say zero G all the time and the kids are confused. How do explain that gravity exists everywhere, and then they hear of zero g on the space station ?

ANSWER:
First, let me say that your example (which I have not included here) is not a good one. Let me attempt to give an answer to the question regarding zero-g (sometimes referred to as weightlessness). Those terminologies are, strictly speaking, incorrect. What is your weight? It is the force which the earth exerts on you. It is not what is measured by a scale; a scale measures the force you exert on it, not the force the earth exerts on you. Of course, in every day life the force which you exert on the scale happens to equal your weight, but if you are in an elevator accelerating up the scale will read more than your weight. If you are in an elevator free falling down, the scale reads zero but your weight is still the same. If you say zero-g you imply that the gravitational field is zero but that is certainly not true anywhere near the earth (except at that point where the earth's and moon's gravity cancel). I presume that you have taught your students about centripetal acceleration. Anything which moves in a circle of radius R with speed v has an acceleration toward the center of the circle of v²/R. A satellite in a circular orbit has just the right speed such that this acceleration is equal to g so, as you correctly state, it is the same as the free falling elevator�you feel like there is no gravity. All this is standard physics.

Here is another perspective: Einstein's principle of equivalence states that there is no experiment you can do to distinguish whether you are in a gravitational field or in an accelerated frame of reference (that is, the freely falling elevator and having zero gravity are physically indistinguishable from inside). So, if it looks like a duck and quacks like a duck, we might as well call it a duck!

(One final note: Note that I have ignored the tiny correction that if you are orbiting with your feet "down" your feet have a slightly different acceleration from your head.)

QUESTION:
What exactly is in light that makes it be affcted by gravity? please give me a thorough informtion about what light contains that is affected by gravity.

ANSWER:
See an earlier answer.

QUESTION:
Assume an electromagnetic wave in vacuo. From my reading, I infer: 1: that a photon is a single cycle os a wave 2: that each change in the orbital level of an electron produces one photon. 3: that the intensity of light emitted from a source is governed by the number of atoms in which electrons are changing orbital level 4: that the basic difference between "ordinary light" and lased light is that in lazsed light the photons are brought into tandem as a continuous stream (wave) of photons. 5: that the energy of the photon is equivanent to the energy lost by the electron during the orbital transition.

ANSWER:

As in your question below, a photon is not a wave at all.
true
true (number/second decaying)
essentially correct. The waves (think of waves, not photons) are coherent, that is they are all in phase with all the others.
true, but I would say energy lost by the atom rather than by the electron.

QUESTION:
Is there a fixed relationship between the wavelength of a photon and its amplitude? Electromagnetice waves are usually graphed as two perpendicular sine waves. But I suspect that they must extend laterally to some extent. Is the shape if viewed longditudinally known? Can to direct me to a site that would dispaly such?

ANSWER:
A photon is a particle, not a wave. So it does not have a wavelength or an amplitude in terms of electric and magnetic fields. A photon has fixed energy so that if you think about the wave which is equivalent to the photon, its amplitude will be determined by how spread out in space it is, that is by the uncertainty as to where the photon is.

QUESTION:
I have read that according to Einstein's theory, if a person were able to travel at the speed of light, they could stop time completely, and slow time (from people on Earth's perspective) if they were to travel near the speed of light. Also, I read that the greater the gravitational force, the slower your biological clock would run. Why would scientists not utilize this theory in humans to slow their biological clocks and thus allow them to see a greater future? It is probably possible with certain machinery to elevate the force of gravity within a unit.

ANSWER:
You are breaking the rules! No questions about traveling the speed of light! I can give you two reasons we don't accelerate humans to velocities near the speed of light:

The energy it would take get you going to 99% the speed of light is huge.
Even if we were willing to invest the energy is such an adventure, your acceleration would have to be so enormous that your body would be crushed beyond all recognition.
Similarly, you body would not be able to remain uncrushed in a huge gravitational field.

QUESTION:
If i have a superconductive wire and i attach a positive electrode to one end and a negative electrode to the other end there will be some measurable current through the wire. every time i recreate this circuit within the same parameters the same current will be read. not any current, only this current. if the wire were thicker (assuming that the cross sectional area of the electrodes were increased the same extent) , more electrons would be able to flow through the wire. thus the current would become greater. if were to replicate this circuit i would again read this same greater current, not any. to my understanding a potential difference is increased when the ratio of electrons to protons on the positive electrode increases or when the ratio of electrons to protons in the negative electrode decreases, thus the attractive force between the departing electrons in the positive electrode and the immovable protons in the negative electrode would in increase with increased potential difference. i acknowledge that my conceptualization of potential difference mat not be correct, but if it is why would placing a positive and negative electrode to either end of a superconductive wire result in a potential difference of zero? would the electrons not flow more quickly through a superconductive wire if the attractive force between them and the positive electrode is greater?

ANSWER:
By definition the potential difference across zero resistance must be zero. When you connect a power source across it, the voltage across the terminals must drop to zero or else the wire must go nonsuperconducting. I have answered this question many times. You might be interested in searching through previous answers for superconductor.

QUESTION:
I have a few unanswered questions about gyroscopic precession. I looked thought the archive but I haven�t found anything that directly answers my question. I understand if you spin up a gyroscope, put It down at an angle, its axis will precess around in a cone. I further understand (and correct me if I am wrong about this) that in a completely frictionless environment it will precess forever around its center of mass. This strikes me as similar to a spinning an object in space. Spin it once and it goes forever baring friction and outside influence. However in the case of the gyroscope where does the initial energy come from to start in precessing? Does it tilt slightly more upon release thereby lowering its center of mass and make use of some potential energy? Does the gyroscope itself reduce speed slightly? If we assume one of these things is true than it would seem the energy would have to go somewhere once the gyroscope stops precessing. For instance say we built a half circular frictionless tack that is the correct height such that it supports the gyroscope once it gets to it, without lifting it. Now, when the gyroscope reaches the track it should stop precessing because there is no longer a tilting force applied to it. However if the gyrocope initially derived energy for precession from a slight drop or a decrease in rotation, does the reverse happen? It would seem that it could not rise back up because then it would then have a tilting force again. Does the gyroscope gain rotational speed?

ANSWER:
Your question comes close to violating the "single, concise, well-focused questions" groundrule! Let's start out talking about translation instead of rotation. Suppose you have a particle moving along with some momentum and then you apply a force which is perpendicular to its momentum; the result is that the momentum changes (its direction, not its magnitude). This is because of Newton's second law which is often more useful in the form of force equals rate of change of momentum than force equals mass time acceleration. For rotational motion, Newton's second law takes the form that torque equals the rate of change of angular momentum. The gyroscope will not precess if there is no torque on it, that is, if it were in empty space, it would not precess. Like in the case of the particle above, the angular momentum changes its direction rather than its magnitude; the spin rate stays the same but the spin axis changes its direction. If you were to suspend the gyroscope so that there were no torque on it (as in gyrocompasses, for example) it would not precess. Most of your questions are sort of not answerable because you did not understand the basics which I have tried to convey. The motion is actually more complicated than it appears but is well-understood; it depends on the initial conditions but usually includes small wiggles (called nutating) about the precession which are usually damped out quickly by friction in real systems.

QUESTION:
if one has a circuit containing a superconductive wire with a certain cross section of area, there will exist some measurable current unique to this cross section of area. even though there exists no electrical resistance through the wire there is still a definite number of electrons which can fit within the wire's cross section of area, all traveling at some velocity. how does a definite number of electrons unique to a given cross section of area all traveling at the same velocity not result in some definite current unique to a superconductive wire with this cross section of area?

ANSWER:
What makes you think all the charge carriers would have the same velocity? Your argument could equally well be made for a normal conductor. In fact, all the charge carriers are in motion and the faster the average motion the larger the current.

QUESTION:
If I sent you in a spaceship to Alpha Centauri or say, Vega, and spun you in a circle, how would you reliably return to Earth? Since those are relatively close, what about the center of the Milky Way? I'm basically asking, since you would be at a different point in the universe, how would you reliably navigate back to Earth since the sky would look very different? The difference might not be too great at Alpha Centauri, but at say, the center of the Milky Way, I can't imagine how you would know which direction you came from if you were "spun" around to face a random direction once you got there.

ANSWER:
You underestimate the power of computers in the current state of celestial navigation. All you need to know is the position (say relative to the sun or maybe relative to the center of the galaxy) of as many recognizable stars as possible. Then any even modest computer could easily calculate how those stars would appear to you as seen from anywhere.

QUESTION:
I understand that when an atom makes a transition from one state to another it emits a particle of light called a photon.. well now, is the photon in the atom ahead of time that it comes out? or is there no photon to start with? and if there is no photon to start with then where does it come from and how does it come out??

ANSWER:
Let's first discuss a radio station. The way we broadcast the radio waves is that we cause electrons to move back and forth in the antenna. These wiggling electrons cause the waves to be emitted from the antenna. Did these waves exist before we started wiggling the electrons in the antenna? Were they somehow sitting there waiting to be sent off? No, of couse not. The wiggling electrons created them, not from nothing but using the electrical power we put into the wiggling electrons in the antenna. For example, if we put 50 kilowatts into the antenna, then 50 kilowatts of radio waves will come out of it. Now to your question. The excited atom is like a little antenna; when the atom drops to a lower energy state the electron has to change the way it moves in the atom, sort of by wiggling into the new state. But the atom lost energy equal to the difference between the two states, so electromagnetic energy is radiated away, the photon which is the smallest possible bundle of electromagnetic wave.

QUESTION:
What is meant by " Protons gyrating at very high magnetic fields"?

ANSWER:
I have not this expression before. It probably refers to the precession of the proton's magnetic moment in the magnetic field. This is just the same as a top which precesses in the earth's gravitational field. I can't say more than that without knowing the context of the quote.

QUESTION:
i understand that all is always in motion & therefore changing/transforming/decaying. My question is what does gold change to?

ANSWER:
I have no idea what you are talking about. Just because something is in motion does not mean that it is "changing/transforming/decaying". A passing car is in motion but not changing into something else. Gold is a stable element and does not change into anything.

QUESTION:
Given a circuit comprised of superconductive material and a known voltage how could the current be calculated?

ANSWER:
I have answered this question a couple of times before. What it boils down to is that if the resistance is zero the potential difference is zero. You simply drain the power source by shorting it out. The current can be anything and the voltage must be zero.

QUESTION:
We have just started a physics project and I was wondering if you could offer a little help. Our teacher hung a remote-controlled plane from the ceiling by a string. He turned it on and waited until it reached a constant velocity (it travelled in a circle). Then he timed how long it took for the plane to complete 15 revolutions. Our job is to find out how long it took for this to happen. We are allowed to take any measurement we want execpt for measuring the time. The mass of the plane is 29.6g. The length of the string is 2m 90cm. The radius of the circle in which the plane travelled is 2.37m. I'm not asking for an answer for this project but I was wondering if you could give me some ideas and inspire me. Heh heh. Every time I try to plug it into one of our distance, acceleration, momentum, etc. equations I hit a dead end. I have an idea about using the angle that the string was at to somehow play into this.

ANSWER:
This pretty much sounds like homework, so I cannot tell you how to do it. I will give you a hint: the vertical component of the tension in the string must be equal to the weight of the plane. Look up the analysis of the spherical pendulum. Incidentally, you should not say that the plane has constant velocity, it has constant speed. Velocity is a vector and since the plane's direction is constantly changing its velocity is constantly changing.

QUESTION:
My friend received a speeding ticket a long time ago on a motorcyle. He says it was for a speed much faster than he was ever going. He says a knowledgeable person told him that the false reading was due the the motorcyle wheel spokes going faster than the speed of the motorcyle, or the velocity of the spokes adding to the motorcyle speed. Its been a while since I took a basic college physics class, but it seems to me that the if the bike is going speed X, the circumference of the tire - the part that contacts the road, has to be going the same X. If the tire tread is rolling out at a velocity of X, any spoke - being less far from the axle, has to be going less than X. EG, the spoke cant be going faster than the speed of the bike. Is it physically possible parts of a motorcyle wheel can indicate on a radar, a speed that is faster than the actual speed over ground of the motorcyle?

ANSWER:
The axel of a wheel goes forward with the speed of the vehicle, the bottom of the wheel is at rest, and the top goes forward with a speed twice the speed of the vehicle. Any particular spoke might have a forward speed anywhere from about zero to about twice the vehicle speed depending on where you look. I would say that the likelihood of the radar reading the speed of a spoke is virtually zero. Either your friend was mistaken about his actual speed (likely) or the radar malfunctioned. The speed of the spoke argument is not likely to be the explanation.

QUESTION:
My question is about light. If light is affected by gravity, what is in light that makes it be affected like any other matter? I know that light is affected by light because they are pulled into blackholes. Try to make two answers....one answers for a 6th grader (easy) and one for a teacher level (confusing).

ANSWER:
I have answered this question previously. The answer has a part geared toward an 11 year old and another from the perspective of warping spacetime.

QUESTION:
why does it become significantly easier to balance a bike the faster you are going (either pedaling it or say going down a hill)? For instance, it would be very difficult to balance on your bike if it was standing still, less difficult when you first start to pedal away, and even less difficult when you get some speed. I can balance with no hands best when my bike is moving swiftly. Why is it that the additional speed results in easier balance? And is there a point of diminishing returns, like a point at which the additional speed doesn�t help you but hurts your balance? Let�s assume for all of this that we are on a �good road,� i.e. you aren�t trying to balance your bike on a rocky trail or something.

ANSWER:
This is actually a tricky question and one which requires more space than I can give to a single answer. The glib answer would invoke the gyroscopic behavior of the spinning wheels but, although this is often cited in elementary physics classes as an explanation for steering a bike it turns out to be a very small part of the explanation of bicycle stability. Here are two sites where you can get a pretty lucid explanation:

http://en.wikipedia.org/wiki/Bicycle_and_motorcycle_dynamics
http://socrates.berkeley.edu/~fajans/Teaching/bicycles.html

Or, you can do a google search on physics of bicycle.

QUESTION:
Particle accelerators take up alot of space, would it be possible to make them take up less space by making them in a dense curled corkscrew shape?

ANSWER:
A particle with extremely high energy is extremely hard to deflect from a straight path. Even using the strongest magnets available (superconducting magnets) only a modest deflection of the passing beam of particles can be achieved. So it is simply not possible to bend them around a closed path in a very small space. An interesting detail is that once you get very close to the speed of light, the magnetic field does not have to be adjusted to compensate for the greater energies as the particles gain energy; a magnet will bend a 500 GeV proton just about the same as a 1000 GeV proton, so you can use the same path for the particle as it is accelerated. The accelerator does not really accelerate the particle much at all as the energy increases (like a proton traveling at 99.9999% the speed of light would have a much higher energy than one with a speed 99.999% but almost the same speed). So accelerators would be better named energizers than accelerators!

QUESTION:
how much percentage of light would be lost if light (say a flash light) was shot into a box with the dimensions of 1ft. by 1.ft by 1 ft., filled entirely with the best reflecting mirror found in the world?

ANSWER:
All of it, and very quickly. See an earlier answer to get a perspective on how fast the light would be lost. Incidentally, the light is not really lost but is converted into thermal energy when it is absorbed by the mirrors.

QUESTION:
What effects would we feel if a black hole approached the earth? What would happen to our orbit around the sun and the moon's orbit on us?

ANSWER:
That depends entirely on how massive the black hole is and how closely it approaches. If the earth were inside the event horizon, it would be swallowed up.

QUESTION:
As I understand the Quantum Mechanics double slit experiment an electron (or photon) is shot through a wall with two slits. If there's an observer (which I understand to mean any force that impacts on the experiment's system) then the electrons hit photoelectric paper as if the electrons were particles, in other words they hit in one and only one place. If there isn't an observer they hit as a probability wave. My question is, why isn't the photoelectric paper considered an "observer" since it clearly interferes with the system, in fact it's there to observe the behavior. Given my limited understanding of the Quantum Eraser experiment I don't see why time should have an impact on the recording of the electron's hitting the paper.

ANSWER:
You do not have it quite right. It is not "if there's an observer" but rather whether the observation makes a measurement which tells you which slit the electron (or photon) passed through. If you make this determination, the interference pattern does not appear.

QUESTION:
a single photon of red light does not possess sufficient energy to remove an orbiting electron from its nucleus. in theory, if more than one photon were to contact one electron (of course quite an improbable scenario) could the combined energy of the photons potentially cause ejection of the electron?

ANSWER:
Yes, it is called multiphoton ionization. It is practicable with high-intensity lasers.

QUESTION:
I am holding a 20 newton object at arms length a constant 1.5 meters above the ground. My body will clearly be expending energy to maintain the object at that height. How do I calculate the rate of energy expenditure (power) required to hold the object at the specified height? This problem is vexing to me, because the same object could be placed on a stationary 1.5 meter platform to accomplish exactly the same thing, but the platform will obviously not have to expend any energy. I am having trouble understanding exactly how these scenarios differ.

ANSWER:
This energy which you perceive as being consumed is not going into the object you are holding up. There is no work being done on it. I agree that some chemical energy will be used by your body to achieve this, but there is no way to calculate this since it depends on the individual's fitness, metabolism, etc. The energy expended would end up in thermal energy and would be used for the biochemical reactions necessary to maintain the required tension in the muscles.

QUESTION:
When two objects come into contact (say my buttocks and a wooden chair) does an exchange of matter occur between the two? If so, what gets exchanged? Do they, for example, exchange electrons?

ANSWER:
Yes, of course. Untold millions of atoms go both ways. But millions is a really small number compared to the total number of atoms in the objects (like on the order of 10²⁴). But, ultimately this is why clothes get dirty, clothes wear out, things have to be repainted now and then, etc. Also, electrons can go one way or the other which is why you sometimes have a static charge on you after rubbing on something.

QUESTION:
If a free electron interacted with a photon (in a vacuum if it helps), what would happen? For example, would the photon reflect off the electron, or does it depend on the motion of the electron?

ANSWER:
It depends on the energies of the electron and photon. If their combined energies are high enough then production of elementary particles could happen. For example, the photon could convert into an electon-positron pair. I suspect that is not really what you are asking, though. Regardless of the energies, the most likely interaction is simple elastic scattering, the photon and electron have the same total energy and linear momentum as before the scattering but move in different directions than before with different shares of the energy. The best known example of such scattering is called Compton scattering. This is probably what you refer to as "reflect off the electron".

QUESTION:
1. Using a conversion factor such as (12inches/foot), the conversion factor is equal to what? 2. How to convert mm to meters? 3. How to convert ms to seconds? 4. How to convert cm to meters?

ANSWER:
The key is to multiply by 1 so the units come out the way you want them. For example, suppose you wanted to convert 73 miles to centimeters: 73 mi(5280 ft/1 mi)(12 in/1 ft)(2.54 cm/1 in)=73 x 1.61 x 10⁵ cm =1.175 x 10⁵ cm; note that each quantity in parentheses is 1 even though it is numerically not 1. The ones you ask for are easier: N mm(1 m/1000 mm)=N/1000 m; N ms(1 s/1000 ms)=N/1000 s; N cm(1 m/100 cm)=N/100 m.

QUESTION:
I'm trying to see I have the right "image" in my mind of how photons work, specifically in the photoelectric effect. Suppose someone was trying to free electrons from a metal by using light. Would this mean that even though an individual photon can have a range of energies the amount of photons must be an integer number? The "image" in my mind is someone trying to break a window by throwing an (integer) amount of small projectiles, but he has the choice of rocks or ping pong balls. He could use a thousand times more energy throwing a million ping-pong balls at the window, than using a single rock, but the single rock will break the window (minimum frequency can release an electron) while throwing ping pong balls does nothing (does not release an electrons).

ANSWER:
I guess your visualization is ok. Your ping pong balls would represent photons with energy smaller than the energy required to remove an electron. Your rock would represent a photon which does have enough energy.

QUESTION:
I teach third grade and students have built a ramp and are using a toy car without mass and with mass to see if the distance increases with mass. The car should go further, correct? But why in third grade terms.

ANSWER:
I have addressed this question twice before. If you read those answers you will find that yours is not a simple question easily answered in terms of basic physical laws. There are too many complicating factors and friction is not nearly as clean a topic as it is often represented in elementary physics textbooks. I am assuming your ramp takes the car down to a flat surface. If there were no friction, the loaded and unloaded cars would move exactly the same and would keep going forever. If the friction were proportional to the weight, (which is what an elementary physics textbook will tell you) the two cars would still move identically and go the same distance before stopping. So, this experiment is a good example of an experiment you can do to see if the simplest physics works. If not, tell your kids that what scientists do all the time is test accepted theories and when those theories fail the scientists try to figure out why. Since you are using the same car for both tests, I would think they would go about the same since the friction should roughly double if you double the weight.

QUESTION:
Doesn't a photon have to have a mass equal to its energy divided by the speed of light squared?

ANSWER:
The trouble with having a well-known equation like E=mc² is that it is often used when not appropriate. If you write E=mc², then this is the energy of a mass which is at rest; or else it means that the mass has a different meaning from what you usually think of when it is moving with speed v, namely m=m₀/√(1-(v²/c²)) where m₀ is the mass of the particle at rest, what you usually think of as inertial mass. As I have said in many earlier answers, I prefer to not think of mass as increasing with velocity, m to me just means rest mass. The correct equation for energy is E=√(p²c²+m²c⁴) where p is the linear momentum. So, if a particle is at rest, momentum is zero and E=mc²; if the mass is zero (as is the case for a photon), E=pc. So a photon has momentum even though it has no mass. One thing to be careful of, as explained in my earlier answers, is that momentum is no longer mv but rather mv/√(1-(v²/c²)).

QUESTION:
Has the superstrings theory been discarded?if yes why if not then what are these strings made of?

ANSWER:
String theory is still a very active area of research. However, many physicists, including myself, are not attracted to a theory which cannot make any predictions about nature which seems to be the case with string theory. It is not an appropriate question to ask what the strings are made of; supposedly everything else is made from them.

QUESTION:
A classic paradox in Greek philosophy is the paradox known as "Zeno's Paradox" which involves the race between Achilles and the Tortoise. According to this paradox, Achilles must traverse an infinite number of points to overtake the Tortoise, which is physically impossible and yet he does in fact overtake the tortoise. Hence the paradox. Most people have thought that the concept of "Limit" in calculus has solved this paradox, but apparently such solutions don't do justice to the paradox in it's original form. (See the entry on wikipedia on Zeno's paradox). It has been suggested that the correct solution comes from Physics directly. In other words it is better to consider that space-time is not infinitely divisible but is rather essentially discrete and that motion is actually a series of jumps from one quantum space-time coordinate to the next. This solves the Paradox since now Achilles actually traverses a finite series instead of an infinite one.

ANSWER:
I don't think any serious logician finds anything paradoxical about Zeno's paradox. There is no need to discretize space to get a more satisfactory explanation. If we assume space is continuous there is still no problem understanding why the fast catches up with the slow. However, the question of whether or not space is in fact continuous or discrete (as well as time) is an open one and of interest to physicists, particularly those studying quantum gravity. I have previously answered a question similar to yours.

QUESTION:
An ideal gas is inside an insulated container so heat can't escape. If the cas is compressed, according to the first law, internal energy is increased so temperature increases - am I right? If so, why does the temperature increase? The temperature relates to how fast molecules are moving. I am thinking that if they hit against a piston coming at them, they will rebound faster - am I right? This would explain the temperature decrease if the gas expands If I am right, I am thinking that if the piston is moved very slowly compared to very fast, I would expect a different final temperature - am I right? Also, why does gravity seem to have no effect on molecules. If gravity has any effect at all, I would expect all the molecules in the container to eventually end up at the bottom of the container if is left alone for a very, very long time.

ANSWER:
The first law is energy conservation. If you arrange so that no heat goes in or out of the gas, then the work done on the gas must equal the increase in energy of the gas. This is called an adiabatic compression (AC). It may be shown that for AC the pressure and volume are related by PV^γ=constant where γ=C_p/C_vand C_p and C_vare the specific heats of the gas at constant pressure and volume respectively. The work done on the gas when you go from P₁, V₁to P₂, V₂is W=(P₂V₂-P₁V₁)/(γ-1). One can easily relate this to the temperature change because work may also be written as W=C_v(T₂-T₁). All the details can be found in any introductory physics textbook. Your qualitative analysis of the moving piston speeding is the gas molecules is a good one. There is no reference in my remarks above about how you get from 1 to 2, so your expectation that the temperature change depends on how rapidly your compress the gas is not right; when you go slowly you give the molecules many little kicks but when you go rapidly you give them a few big kicks. In the real world we usually want the compression to be fast to guarantee that it is adiabatic because it is hard to make a really well insulated cylinder so if you compress slowly heat is more likely to leak out as the gas heats up. But, if it is well insulated it should make no difference. Regarding gravity, it does have an effect but, because the molecules are restless (they can't all settle at the bottom because they keep moving around if the temperature stays constant), the effect is smaller than you expect. In fact, the density of gas at the top of a container is very slightly smaller than at the bottom. You might find this difficult to believe, but it happens for the same reason that the density (pressure) of the air decreases with altitude.

QUESTION:
I just emailed you some very basic questions about thermodynamics. One of them was why gravity doesn't cause all ideal gas molecules to evetually settle at the bottom of the container. I am thinking now that this may be due to the temperature of the walls of the container. Since the walls are at the same temperature, maybe the motion of molecules in the walls excites the gas and keeps that from happening. I feel like these are all dumb questions because they seem so basic - yet I don't remember these questions being answered in school, although it has been a long time.

ANSWER:
Your questions are not dumb. When we derive the ideal gas law we assume that the collisions of the molecules with the wall are elastic, that is no energy is lost or gained in a collision. This is not necessarily true for any given collision but, if the gas and the walls are in thermal equilibrium, it will be true on the average, just as many collisions gaining energy from the walls as those losing energy. When you are dealing with something like 10²⁴ atoms, the average is what matters, not one particular event.

QUESTION:
On Saturday I visited my sister in freezing eastern Pennsylvania and I noticed a strange ice formation in her outdoor birdbath, which is currently frozen due to subfreezing tempertures. This is a cheap 12 dollar birthbath, it is not heated. I would like to send you a photograph of the gravity-defying ice formation and hope a physicist can tell be what law of nature would cause water in a birdbath to freeze up into a small column.

ANSWER:
This question has been previously answered.

QUESTION:
I've never quite fully understood the classic "bicycle wheel and spinning chair" demonstration. Specifically, I've never understood the middle stage, in which the wheel is rotated 90 degrees, rather than the full 180. At this stage, the student should be rotating around a vertical axis in the same direction in which the wheel was initially spinning (say, clockwise), with the wheel's initial angular momentum. But the wheel is itself still rotating (around a horizontal axis) with its full initial momentum. There seems to be a new angular momentum vector, orthogonal to the system's initial angular momentum and equal to it in magnitude, that was not introduced by an external torque. What am I missing?

ANSWER:
Imagine that you are in empty space where angular momentum must be conserved. You start with angular momentum L₀ which is parallel to your spine, say. Later the wheel has angular momentum L₀ perpendicular to the original direction of your spine. So the change in angular momentum of the wheel is in a direction 45⁰ relative to the original direction of your spine so that is the axis along which your angular momentum must have to conserve angular momentum. When you do this experiment you should feel like something is trying to push you off the stool but you can only rotate about an axis parallel to your spine so angular momentum is not actually conserved; the friction between you and the stool exerts an external torque.

QUESTION:
They say that the blackholes' gravitation is so massive that it devours light but the photon has no actual mass so how is he attracted to the hole?

ANSWER:
Light is affected by gravity just like mass. The reason it is not evident is that light travels so fast. Imagine a baseball zipping by at near the speed of light; you would be hard pressed to see at drop much as it zipped by. It has been observed experimentally by observing the bending of distant starlight as it passes close to a massive object, for example the sun during a solar eclipse. This is all understood in the theory of general relativity where the explanation of gravity is that massive objects actually warp the space around them and when light is bent by gravity it is simply following a "straight line" in this warped space.

QUESTION:
What is heat or thermal energy on the atomic or sub-atomic level? Is it the nucleus spinning or perhaps the nucleus is bouncing around relative to the electrons? Do we even know or have theories?

ANSWER:
First of all, heat is energy transfer, not energy content. For example, heat flows from a hot object to a cold one but you do not say that the hot object has more heat than the cold one. If we refer to the internal energy of something, for example a gas, it is the average energy per constituent; it is this average energy which temperature measures. In a gas this is the average kinetic energy per molecule. So let us define thermal energy as average energy per constituent. Then in a nucleus the average energy per nucleon is the "thermal energy". A "hot" nucleus is a highly excited state.

QUESTION:
From a previous question a basketball zipping by at a substantial percentage of the speed of light will have its apparent shape change from sphere to an oblate spheroid because of the shrinking along the direction of motion. This will cause a decrease in its volume and surface area. If the basket ball is replaced by a black hole will the decrease in surface area cause a corresponding decrease in its entropy and mass?

ANSWER:
First, it is wrong to refer to its "apparent shape". Relativity tells us how things are, not how things appear to be. Length contraction says that a meter stick moving by (parallel to its own length) is actually shorter than one meter if we make a measurement of its length. (The operational definition of length is to measure the positions of the two ends of something at the same time.) Regarding entropy, I believe the article I referred you to in the earlier answer showed that entropy, like temperature, is not a useful concept in relativity. The mass is also an ambiguous thing; many people simply envision mass as increasing with velocity, but in many earlier answers I have argued that one may simply say that rest mass is the useful concept and momentum is no longer defined as mass times velocity.

QUESTION:
If a basketball zips by at a substantial percentage of the speed of light will its shape still be a sphere or will the length contraction in the direction of motion cause the shape to change? If the shape is different would the volume be the same or would it change and the pressure of the air inside change?

ANSWER:
The diameter of the ball along the direction of motion will get smaller so the ball will not be a sphere. The volume therefore gets smaller as measured by an observer seeing it zip by. The volume will be reduced by a factor of √(1-v²/c²). That is the easy part of the question. The question concerning the pressure is a very difficult one and I have not found anybody who can give me a definitive answer. I have done a little research and have found more information about temperature than pressure in special relativity. There is a what is called the Planck-Einstein transformation for temperature: the temperature of the gas in the passing ball is reduced by the same amount as the length, that is √(1-v²/c²). So if we now assume that the ideal gas law, PV=NkT, is correct in the moving system, then if V'=V√(1-v²/c²) and T'=T√(1-v²/c²), it follows that P'=P; the pressure is unchanged. That is all well and good, but recent research has shown that the Planck-Einstein transformation is incorrect. In fact it appears that there is no Lorentz transformation for temperature which essentially means that temperature as we define it is not a useful variable in relativity. I suspect that the same could be said for pressure, that is it is not a variable which we could transform into a moving system, there would not be a way you could measure pressure in your moving ball. That is the best I can do with this question. If you get a better answer somewhere, I would be most interested in learning what you learn.

QUESTION:
My husband and I are having a disagreement on the energy used to air dry laundry indoors. He argues that it is less energy efficient than, or at least the same as. running the gas dryer, to air dry laundry indoors in winter because then the house heating system has to work harder to convert the water molecules in the clothes to liquid and gas. I don't have a good answer for him, but it just seems counter-intuitive. It seems like the air drying clothes are at the same temperature as the surrounding air, and don't need heat to "wam up" the water in the clothes. It also seems like the water in the clothes would evaporate due to the dry air (some mumbo jumpo about liquid/vapor equilibrium), not because of heat energy being transferred to the molecules. He doesn't deny that air drying provides moisture to the room, his argument is that the energy required to evaporate the water ultimately comes from the furnace so we might as well run the humidifier and the gas dryer. What do you think?

ANSWER:
Your husband is not going to like this, but he is dead wrong. You could turn your furnace off and your clothes would dry just about as fast. Certainly air drying clothes takes energy from the environment, but the amount is trivial compared with how much your furnace needs to put out to keep your home warm. Believe me, your furnace will never notice. Yesterday it was about 35 degrees at my house and I hung out clothes which dried in about 2 hours. Clothes dryers are among the biggest energy hogs of all our appliances because so much of the energy goes out the exhaust or heats up the dryer drum or just leaks away in some other way. When I started hanging out my clothes instead of putting them in the dryer my electric bills went down about $20 per month. Here is another thing (ok, this is kinda off the wall!): if you dry your clothes in the house it will humidify your house which makes it feel warmer so you can actually turn the furnace down!

QUESTION:
How can Bob who lives in a 2 dimensional world (a) discover the 3rd dimension (b) imagine the 3rd dimension?

ANSWER:
This is a pretty open-ended question. Let me give one example. In some respect you live in a two-dimensional world because you live mostly on the surface of the earth. If you did not understand that your two dimensions were embedded in a three-dimensional space you might be inclined to think that you were on a big flat plane. But, if you started walking due west you would eventually get back to where you started from and you would start thinking maybe there were higher dimensions.

QUESTION:
Simple: All mass gives off a gravitational field. The more mass the stronger the field as well as the greater it's area of effect. Density is the amount of matter in a given space. So my question is: If you take all the matter in the Earth and increase it's density by two will the gravitational field effect space and matter the same as at normal density or will the area of effect half it's size while it's gravitational field strength doubles? This ratio is off the top of my head but an equation with explanation of the variables if ones exists will suffice.

ANSWER:
What you describe will double the mass of the earth. The result will be that the gravitational field due to the earth will double everywhere. I do not understand what you mean by "...the area of effect...". The gravitational field extends to infinity regardless of its strength.

QUESTION:
What does it mean when a field is represented by 2nd-rank tensors (Einstein's gravity)? If a scalar (0-rank) is a numerical quantity representing magnitude, and a vector (1st-rank) is a magnitude that has a direction, then is a matrix (2nd-rank) a plane represented by orthogonal vectors (squared magnitude/perpendicular directions)? Have 3rd-rank tensors ever been used in any physical theories?

ANSWER:
This is really too technical a question for the purposes of this web site. I can tell you that a physically observable quantity may be characterized by how it transforms under certain tranformations; examples of transformations are translations, rotations, space reflection. If you are doing physics in an N-dimensional space then you need one number to specify a scalar quantity, N numbers to specify a vector, N²to specify a tensor (although symmetry proporties usually reduce this number, maybe something like T_ij=T_ji), etc. I do not know how to answer the question "what does it mean", it simply is what is mathematically necessary to describe accurately something in nature. An example more accessible than gravity is perhaps electromagnetism. Here we may describe the electromagnetic field by specifying two 3-dimensional vectors, the electric and magnetic field; this requires 6 numbers. However, the field may be alternatively represented by a single quantity, the field tensor, also containing six numbers but having the elegance of a single quantity rather than two.

QUESTION:
I was reading the short article: Scientists Expose Light's Wierd Quantum Nature, #65, pg 56- Discover Magazine-The Year In Science-Jan 2008. Isn't Light's quantum nature fairly obvious taking the macro approach? For instance...if two planets were one light year apart...and planet A flashed a bright light at planet B...wouldn't the guy on planet B be able to look through a (very powerful) telescope focused at 1/4 the distance in three months and see the same flash that he would be able to see three months later by focusing at 1/2 way point, and three months later focused at the 3/4 point? In other words, the same event would not only exist in an infinate number of places at an infinate number of different times, but given the spray effect over that far a difference, would exist at an infinate number of focal points from an infinate number of points of view...wouldn't it?

ANSWER:
Your telescope does not allow you to observe someplace instantaneously as you assume. When you focus your telescope at the 1/4 the distance point you see light which started from there 9 months ago, not light coming from there right now. If you focus your telescope there you will see your sought pulse in your telescope in 9 months. And so forth.

QUESTION:
A middle-aged man typically has poorer hearing than a middle-aged woman. In one case a woman can just begin to hear a musical tone, while a man can just begin to hear the tone only when its intensity level is increased by 6.0dB relative to that for the woman. What is the ratio of the sound intensity just detected by the man to that just detected by the woman?

ANSWER:
Let D be the intensity in decibels and I be the intensity in W/m². Then the definition of the decibel gives D_woman=D_man+10 log(I_woman/I_man). Then D_woman-D_man=6 dB=10 log(I_woman/I_man). So log(I_woman/I_man).=0.6 and solving I find I_woman/I_man=3.98 .

QUESTION:
If you could lump all of the atomic nucleuses in the human body into a ball, how big would it be? Smaller than the head of a pin? About the size of a pea?

ANSWER:
The size of an atom is on the order of 10^-10 m and the size of a nucleus is on the order of 10^-15 m. So, if we say the size of the body is on the order of 1 m, the size of the nuclear matter in the body would be about 10^-5 m, about 1/100 of a millimeter!

QUESTION:
In a nuclear reactor, what is the importance of particle speed in relation to cross-sectional area?

ANSWER:
I am not sure what you are talking about but have a rough idea, I think. In a reactor, the fuel is induced to undergo fission by absorbing neutrons which makes the nucleus unstable to fission. As luck would have it, when fission occurs several neutrons are produced which may be used to induce still more fissions (chain reaction). However, these neutrons are very fast and unlikely to get absorbed before escaping from the reactor. Hence, to enhance the probablility of these neutrons causing more fissions they must be slowed down (moderation). Slow neutrons are likely to get captured and maintain the chain reaction. So where does the cross section part come in? It turns out that the probability of neutron capture is related to a quantity called the neutron absorption cross section and, as should be evident from the discussion above, the cross section increases as the neutron gets slower. Essentially, cross section is a measure of how big the nucleus looks to the neutron.

QUESTION:
Have you heard of "ball lightning?" If so, is it really lightning? Also, would you know of the microwave ball lightning demonstration, and, if so, what degree of danger it presents as an experiment?

ANSWER:
I have previously answered this question. I don't know what the demonstration you refer to is.

QUESTION:
Does the vapor generated by heating water in a container increase if the volume of water is increased? That is, would 2 cups of water create more steam than 1 cup at the same heating temperature? To me that seems logical, but someone told me that the rate (water) vapor is generated might be limited by the surface area (the same in both cases above).

ANSWER:
The rate at which steam comes off is proportional to the net rate that heat flows into the water and the surface of the water. So having two cups of water in a particular pan on a particular burner does not generate steam at a greater rate than one cup would. (Of course it will ultimately generate more steam.)

QUESTION:
My question is, does the electromagnetic field have a dualistic property? Or is it better understood as a single entity?

ANSWER:
The most sophisticated way to think about it is as a single entity. However, it is more comprehensible if we approach it from a historical perspective (electric and magnetic fields). One reason this approach is easier to understand is that the required mathematics are less demanding: electric and magnetic fields are vectors but the electromagnetic field is a tensor. Also, most devices fall rather neatly into electric and magnetic categories.

QUESTION:
Is hinge a simple machine?

ANSWER:
This is not something physicists really worry about, more often it is important to fourth grade teachers teaching science! It depends on how you define a simple machine. The hinge itself would have a mechanical advantage of 1. The hinge-door system might be considered a lever I guess.

QUESTION:
Have we actualy measured the electromagnetic force of protons and electrons or are there values simply theory?

ANSWER:
Yes, of course we have. The measurements are amazingly accurate.

QUESTION:
I am a 5th grader in Texas and I am working on a science project concerning friction. Could you tell me how friction works?

ANSWER:
Friction is a very complicated thing microscopically and you should probably not, at your age, try to dig too deep since this is not a terribly well understood thing. I would recommend that you focus your project on something like the empirical observation that the force of friction when something slides is proportional to the normal force (the force a horizontal surface exerts upward on the sliding object). This normal force is just the the weight of the object and whatever is stacked on top of it if the surface is horizontal. Therefore, suppose you have a wooden block sliding on a wooden table top. If you measure a frictional force of 1 lb if the block weighs a half pound, then if you add another half pound to the block it should have twice the friction force, 2 lb.. Note that the surface area of the block does not matter, according to this empirical "law". I think it would be a good 5th grade project to test this. I have judged many science fairs and have always found that the best projects are those with a simple, well-focused, interesting, and achievable objective.

QUESTION:
please explain briefly: cold is merely the absence of heat and darkness is simply the absence of light.

ANSWER:
Cold and dark are qualitative terms, not quantitative. If on object is colder than another the energy per molecule is smaller. Dark usually refers to absense of visible electromagnetic radiation but also sometimes can refer to absense or low intensity of other wavelengths. Dark also does not necessarily imply absense but may imply low intensity; when we say it is dark out we certainly do not mean there is absolutely no light.

QUESTION:
To calculate the escape speed from the the earth's surface is straightforward with KE = PE. How would I approach the same calculation if a hole were drilled to the earth's center and I wanted to launch from the earth's center?

ANSWER:
First you must make an assumption regarding the earth's mass distribution. Although not true, most standard problems of the type you present, assume a uniform mass density. In that case you will find that the force on the object increases linearly from zero at the center until you reach the surface. Therefore, the problem is simply a simple harmonic oscillator problem (identical to a mass on a spring). This is a standard problem you will find in many elementary physics textbooks. So you must calculate the speed the particle would need at the center of the earth to have the usual escape velocity at the surface.

QUESTION:
Can an object that is heated only get as hot as the flame that is heating it? I've thought about this question for a while and intuitively it seems that an object can only get as hot as the source. However, if we think of the source as having an infinite source of energy that is supplying heat to an object and that object can only dissipate heat at a certain rate due to radation, convection, etc...then at some point couldn't the object get hotter than the flame? At some point there will be equilibrium but that doesn't limit the object to the flame's temperature correct?

ANSWER:
The flame is not just some object at some temperature, it is a source of energy. An object in a flame can, as you correctly conclude, become hotter than the flame itself since heat will continually flow into the object from the flame and, if heat leaves more slowly, will continue increasing its temperature.

QUESTION:
my question concerns the hypothesized constant expansion of the universe. if the universe is growing exponentially as predicted, would not every object that we use as measurement also expand proportionally? thus it would be entirely impossible to measure such expansion? also, in what way does such an expansion change our view of the universe?

ANSWER:
It is the universe which is expanding, not the space in which it is embedded (although that is changing also but differently). Imagine two cars moving away from each other: would you measure, with a meter stick on one of the cars, that they were not?

QUESTION:
When we drop water on tissue paper, why does it spread evenly ?

ANSWER:
Because of capillary action.

QUESTION:
If everyone in the world began to walk due east at a given time, would the rotation of the earth slow down (in order to conserve momentum)?

ANSWER:
Technically, yes (it is angular momentum conservation). However, the mass of all the people on earth is so small compared to the total mass of the earth that the effect would be too small to measure. (See following question.)

QUESTION:
I wonder: in the event the north pole (artico) thaw completely and turn around the ice water, the balance of rotation of the earth suffer amendments? The masses of the planet will have to be redistribuidas to enter new balance? The axis of inclination of 23 degrees should be amended because of this?

ANSWER:
The total mass of all the water on earth compared to the total mass of the earth is so small that the effect would be too small to measure. (See preceding question.)

QUESTION:
I have question regarding conventional radar systems. As you're aware, stealth technology is based on the notion of reflecting, absorbing, scattering radio signals and cancelling them at the source. Conventional radars look for a positive image of the sky. Rather than looking for a positve image of the sky, what if we look for a negative image instead. If we used naturally occuring or systhesized background radiation, couldn't we passively look for holes at ground sites? In other words, look for the absence of radiation rather than it's presence. Track and triangulate on holes rather than positive returns. Also, if our background radiation source is broad, could we also determine molecular composition of a target through the methods used in spectroscopy?

ANSWER:
In principle you could do something like you suggest. But let me point out a few difficulties:

Background radiation is relatively weak and difficult to receive reliably.

Background radiation is a whole spectrum of wavelengths, some of which would go through, some of which would diffract efficiently around the aircraft.

Because it is a whole spectrum, your detector would have scan frequencies or lock in on one you like, which would further enormously reduce the intensity.

The radiation comes from all directions so you would need very tight directional detection, again greatly reducing the already tiny intensity.

Overall, it is not practical.

QUESTION:
when you walk, do you do any work? The force I believe is perpendicular to the motion (which means no work), but why do you move forward?

ANSWER:
I have previously answered this question.

QUESTION:
How long will carbon dioxide take to disperse in a closed container because of the Brownian effect? How does the Brownian effect work?

ANSWER:
Brownian motion refers to particles suspended, not to other gases or liquids. The carbon dioxide will diffuse into the rest of the gas. The rate of diffusion and the time it takes depends on many things that you have not given information about like temperature, volume, pressure, etc.

QUESTION:
according to Einstein's special theory of relativity the rate of time's progression for any body is contingent upon its speed. Is it posssible to express the rate of times's progression for a body without relating it to other rates of progression (greater or less than another by some factor)? is there some variable, indepedent of time, to which a rate could be expressed with respect?

ANSWER:
In any frame of reference, a clock runs at exactly the rate you would expect it to if you are in that frame. All other clocks run slower than yours if not at rest in your frame.

QUESTION:
There are two objects equal in mass and size and shape... identical blocks of wood for example. They are on a horizontal plane with no friction. The first object moves at 10 mph and collides with the second which is at rest. The two masses merge together (unlike billiard balls,where one stops and the other moves on), and continue as one mass. How fast will the two be travelling after the collision? It seems like it should be half of the speed of the original object, but i was told by a physics instructor that it would be more like 90 percent of the speed of the original object, allowing an arbitrary 10 percent for heat loss in collision. But, doesnt the first object give up some of its speed to the mass of the second object, so that both now move with the same energy at a lower speed?

ANSWER:
Wow, either you misunderstood your instructor or else he has no business being a physics instructor. What you describe is called a perfectly inelastic collision but in any collision where there are no external forces (the only relevant forces here are the forces the two blocks exert on each other) the linear momentum must be conserved, that is remain constant. The linear momentum is the mass times the velocity, and it must be the same before and after the collision. Before the collision the momentum is mv₁ and afterwards it is mv₂+mv₂=2mv₂. Therefore, mv₁=2mv₂or v₂=v₁/2, exactly like your intuition told you. What is not conserved is the energy. Before the collision, E₁=½mv₁²and after the collision, E₂=½(2mv₂²)=¼mv₁². So, you see, exactly half the energy was lost and most of this will show up as thermal energy.

QUESTION:
Has anyone measured the amount of time it takes for electrons to jump from one atomic orbital to another? For example, how long does it take for a stimulated electron in a hydrogen atom to jump from a 99% probability of being in the 2s orbital to a 99% probability of being in the 1s orbital? And, when during the transition does the quantum of energy get emitted?

ANSWER:
You could not make this measurement on a single atom without disturbing the system. The only way to do this is statistically with a large ensemble atoms and the information you get is the transition rate or half life.

QUESTION:
Since water is incompressible, could a deep-diving "chamber" for an aquanaut be built by means of a transparent balloon full of water in which the aquanaut would float suspended without being subject to the pressure of whatever depth the balloon assumed? This balloon would submerge, surface and maneuver by means of machinery external to its surface, controlled (perhaps) via fiber optics links.

ANSWER:
The pressure inside the balloon would increase just like the water on the outside; just because the volume remains constant does not mean the pressure does not increase. Imagine a volume of water in a cylinder with a piston on top and an aquanaut in the water. Now start piling weights on the piston; the volume stays about the same (nothing is perfectly incompressible) but the pressure will increase. Same idea.

QUESTION:
I am trying to figure out a simple puzzle, which is in my head a bit confusing. The puzzle is this: If I mount a cannon on the posterior surface of the earth, that is the rear of the planet as it circles the sun, pointing the camera perpendicular to the plane tangent to the surface, that is apparently straight up as seen from an observer on the ground, and fire the cannon, then the earth should see a tiny increase in speed equal to the momentum of the cannonball divided by the mass of the earth. Then, as gravity slows the cannonball eventually to a stop this increase in speed should be cancelled by the cannonball's pull on the earth. I suppose I am wrong but this seems to be a zero sum situation. Then as the cannonball comes back down and slams into the earth, the original momentum is once again returned to the earth, effectively once again adding speed to the earth. In all of this there is an overall net gain in speed imparted to the earth without any mass being ejected. Since this makes no sense to me I would like to know where my conceptual error lies.

ANSWER:
The cannon fires and momentum is conserved, that is the momentum of the earth plus the cannonball are equal and opposite, adding to zero. Note, however, that energy is not conserved because both the earth and cannonball have kinetic energy; this energy came from the chemistry in the gunpowder. During the whole flight of the cannonball momentum is conserved so that the earth and the cannonball always have equal and opposite momenta. So when they collide they are both moving, the earth "upwards" and the cannonball "downwards". They now collide and stick together; momentum is still conserved, so they must both end up at rest because the total momentum must remain zero and both must have the same speed which must be zero. Energy is not conserved since the kinetic energy disappears; this energy shows up as thermal energy (ball and earth heat up a little), energy of the sound produced, work it takes to squish the earth, etc.

QUESTION:
I've read your answer about a theoretical mirrored room and whether or not the room would remain lit after turning off the light source. My wife has this crazy idea that due to light pollution, even if all the lights in a city were turned off, the glow of the lights would remain for some period of time. I've explained that the if the bulbs were turned off, the existing photons of light would be absorbed, reflected off into space, etc... nearly instantaneously and the entire city would become dark. She insists that the atmostphere would still have light bouncing around and would still give off light. She says that this question won't be put to rest until somebody with serious Physical knowledge gives a complete answer. Can you tell me wife she's being silly and doesn't know what shes' talking about?

ANSWER:
Certainly energy is conserved. However light is usually absorbed and then reemitted as radiation which is outside the visible spectrum. For example, the greenhouse effect is when visible light is absorbed and reemitted in the infrared; the infrared does not effectively penetrate out of the atmosphere so that energy is trapped. But you cannot see it. I agree with you that visible light will almost instantly dissappear when the source is extinguished. An exception would be if you had phosphorescence, the phenomenon behind "glow-in-the-dark" materials, but the air, clouds, and most of the world is not phosphorescent.

QUESTION:
I've read about the wigner effect where exposure to fast neutrons can store energy in graphite that can later be released as heat. My question is, if graphite is exposed to neutrons in a "clean" environment (not contaminated by other radioactive elements) does exposing the graphite to neutrons make it radioactive too?

ANSWER:
This effect is an atomic, not nuclear phenomenon, where atoms of carbon are displaced from their previous locations in the crystal lattice. It is essentially what is called radiation damage and results in such things as electronic components being ruined by exposure to radiation. There is no radioactivity associated with it. That is not to say that there is no radioactivity as a result of neutron activation but I would bet that it would be vanishingly small because if carbon absorbs a neutron (for which the probability is very small) it will simply make another stable isotope of carbon. More exotic reactions could occur but these would be rare. Neutron absorption by impurities in the carbon could also occur, but you presumably would have a pretty pure graphite sample.

QUESTION:
An elementary problem in Newtonian physics is to show that the theory predicts simple harmonic motion of a test object falling through the center of a uniformly dense spherical mass. I've never seen, either in the context of this problem per se or otherwise, any DIRECT empirical evidence in support of the Newtonian prediction. Confidence in the solution appears to be entirely based on observations of motions very far from the centers or beyond the surfaces of gravitating bodies; i.e., extrapolations. It seems to me that the oscillation -- or at least a first approximation thereof -- would not be too difficult to arrange with a suitably modified Cavendish balance. Has an experiment like this ever been tried? If not, why not?

ANSWER:
And the point of this experiment would be…? Gravity is one of the best understood of nature's phenomena and there is really no need to verify each cute little example which has been dreamed up. The idea of drilling a hole all the way through the earth will obviously not work not to mention that the earth is not really a uniform sphere. To do as you suggest is really hard because the Eötvös experiment is one of the hardest around to perform with precision (a group of renoun experimentalists at the University of Washington has been working for years to measure G with great precision this way). The main reason is that gravity is so weak even for objects of mass of tens of thousands of kilograms which you might be able to do an experiment with will experience forces so weak that it might take years for one oscillation to occur. Similar experiments are much easier with electric charges which are also 1/r² forces.

QUESTION:
In a home refrigerator freezer set to 0 degrees F, assuming all the contents have enough space to give up their heat, will all the contents eventually end up at 0 degrees F? I'm aware that not everything freezes (which I read as "becomes solid") at 0 degree F, so some of the freezer contents could still be liquid or flexible (as in sports gel paks). If not all the contents go below 0 degree F, why not? And at the other end of the thermometer, why can I pick up aluminum-wrapped bread just out of the oven with my bare hand? Is the aluminum not as hot as the oven? If not, why not? Thank you very much.

ANSWER:
In an isolated system, which we assume the inside of the freezer approximates, everything will eventually come to thermal equilibrium, that is everything will eventually have the same temperature. Your other question, about the foil, I answered a long time ago.

QUESTION:
I am struggling to understand why it is easy to balance a basketball on your finger when it spins but difficult when it is not spinning. I consider the motion of the center of the ball, since it moves as though all its mass is concentrated there and all external forces are applied there. When the spinning ball tilts slightly so it its axis is at a slight angle from vertical, gravity applies force at the center of mass to pull it off your finger. There must be a countering torque when the ball is spinning to balance the ball on your finger and keep it from falling. Due to the torque from gravity, the ball precesses so its center of mass moves in a circle around your finger. Since the center of mass moves in a circle, there must be a net centripetal force greater than zero acting on the center of mass of the ball. I believe this centripital force provides the countering torque to balance the ball. If the ball was not spinning there would be no countering torque because the center of mass would not move in this circle. The problem I have is that I know that the precess angular velocity (which to my understanding is the angular velocity of the center of mass of the ball as it moves in this circle) is inversely related to the angular velocity of the ball. So the faster the ball spins, the lower the precess angular velocity when it tilts at any angle, and therefore the lower centripetal force and lower countering torque. This seems backwards to me because it seems that there should be more countering torque when the ball spins faster.

ANSWER:
The spinning ball has an angular momentum which is a vector which points along the rotation axis. I will suppose that this vector points vertically up (which means that the spin is counterclockwise as seen from above}. The nonspinning ball has no angular momentum. Now, if the ball starts to fall toward the left as seen by you there will be a torque about your finger which points toward you. Newton's second law states that torque is equal to the time rate of change of the angular momentum, so if the ball is initially not spinning it has no angular momentum so after a short time it has a small angular momentum toward you which means that it is falling to the left; but the torque gets bigger as it falls further so the falling accelerates. Now, if the ball starts with an angular momentum it will be changed also by a small amount toward you but since it already had a lot, its angular momentum vector will change its direction slightly toward you in a short time; this is precession. So, you see that a small error in balance leads to falling for the nonspinning ball but precession for the spinning ball. Now, you simply keep correcting as precession starts which is easier to correct than if falling starts.

QUESTION:
I have some questions regarding strength of an electromagnet
1) Does the size and the material of the core affect the strength of an electromagnet?
2) Does the thickness of the coil affect the strength?
3) The electromagnets I've seen so far had only one layer of coils wrapped around them. Would the electromagnets become stronger if I warp a multiple layer of coils around them?

ANSWER:

The field is proportional to the current around the core and the number of turns per unit length. Therefore the strength is not greater but there is more of it over a larger area. However, the material certainly matters and a ferromagnetic material, usually iron, works best.

Answer 1 covers this.

Again, answer 1 covers this because if you wrap two layers around you are essentially doubling the current.

QUESTION:
What causes gravity? How can gravity be explained? General Relativity, as I understand it, says that gravity is not a force or interaction. Rather that spacetime is "curved" by the presence of mass, and that this curve "tells" other matter ( a test mass?) how to behave. Have I got that right? But the question remains does it not? Accepting what GR says is one thing, but in reality the real question is why or how does mass cause spacetime curvature? Am I thinking correctly here? I teach astronomy at a local school, and some of those kids come up with some tough (for me) questions.

ANSWER:
General relativity starts with a simple premise, the equivalence principle: there is no experiment you can perform which can distinguish whether you are in a gravitational field or in an accelerating frame of reference. For example, if you were in an elevator which was accelerating and a beam of light entered through the side it would follow a curved trajectory to the opposite wall; this is exactly what would happen if you were sitting still in a gravitational field. This principle, coupled with the principle of special relativity (the laws of physics are the same in any inertial frame of reference) leads to the general principle of relativity, the laws of physics are the same in any frame of reference. One implication of this theory is that mass deforms spacetime which is, as you state, how gravity works; mass deforming spacetime is simply a consequence of the postulates of the theory. Is it the last word? Probably not because gravity has not been reconciled with quantum theory and the quest for a theory of quantum gravity is one of the holy grails of physics. I would not say that gravity is not a force just because we understand the mechanism for that force. Asking "why or how" mass causes the curvature is essentially equivalent to asking what is mass, why do objects possess it? The current well-publicized quest for the Higgs boson is important because this is the particle which physicists think is responsible for endowing the elementary particles of nature with mass.

QUESTION:
Are metals more efficient as thermocouples or alloys?

ANSWER:
What does efficient mean in this context? Most sensitive? All common types of thermocouples have one or both metals being alloys.

QUESTION:
Two friends are standing on opposite ends of a canoe. The canoe is initially at rest with respect to the lake. The person on the right throws a very massive ball to the left, and the person on the left catches it. After the ball is caught, the canoe is (ignore friction between the canoe and the water) moving in what direction? A.) To the left. B.) To the right. C.) Stationary

ANSWER:
The linear momentum must be conserved because there are no external forces on the system (boat, ball, and two people). Since it starts out at rest it ends up at rest. During the time the ball is in flight the canoe and passengers must move in the opposite direction, so they do not end up in the same place, but still at rest.

QUESTION:
Can energy exist only in certain quantities, or can it exist at any level, but only be realesed at fixed amounts, or neither? If so what is the minimum amount of energy possible?

ANSWER:
For a given system, e.g. an isolated atom, a mass on a spring (harmonic oscillator), or a beam of light of a given frequency, the energy may only have certain discretized values. The simplest example, the photon, of which the light of frequency f is composed, must have an energy of only hf where h is Planck's constant. Therefore the energy of a beam of that light may only have a total energy of some integer times hf. However, there is no constraint on what the frequency can be and so there is no constraint which says that the energy of a beam of light must be discretized. Similarly, the energies of a harmonic oscilator of a particular mass on a particular spring are quantized; however, there is no constraint on the value which the spring constant can have, so energy itself is not constrained to only discrete values.

QUESTION:
I have a problem with making a contraconcave mirror. Please refer to these links if my question is somewhat incomprehensible...I seem to be having a hard time wording this question...
http://ec.hku.hk/schoolscience/Volumes/Vol_3/SSHK_Vol_3_03.pdf
http://www.wfu.edu/physics/demolabs/demos/6/6a/6A2035.html
http://www.i-am-bored.com/bored_link.cfm?link_id=17162
Anyways, it seems fairly simple enough to make this, however, I am facing two major problems. These are:
1. How can one find out the focal length of any given concave mirror? Is there a formula defined for this?
2. How would the size of the hole in the top mirror affect the mirage produced? If the hole has to be of some exact size, how can one find out what size should it be when making a contraconcave mirror?

ANSWER:
If it were a spherical mirror, the focal point would be half the radius of curvature of the mirror. In the case of a parabolic mirror, the focus is at the focus of the paraboloid. However, It is realatively easy to directly measure the focal length by focusing a distant object (the sun is good) to a point; be careful, though, since the focused sunlight can burn what it is focused on. The hole does not effect the quality of the image because the mirror uses all points on its surface to form the image. Cutting a hole anywhere will slightly reduce the brightness of the image, not its quality.

QUESTION:
I work in an industrial plant and we have air diffusers which are round and have small holes punched in them in a regular pattern. So think of it as a tube about 2 feet in diameter standing on end. The small holes (.125 inch or so) are regularly spaced about .375 inch or so apart. When you stand back from the diffuser you see a pattern that changes depending on your orientation to the diffuser, you see a pattern of much larger light and dark areas that seem to match the pattern of holes in the diffuser (tube) the patterm remains the same, but the size of the pattern will change with distance from the object. I've also seen this same effect when I lay one material with a pattern on top of identical piece of material with the same pattern that is back lit, as you change the orientation relative to each other you see the pattern seem to shift and expand in size. Is this just a complicated version of the interference pattern from the famous 2 slit experiment that proves that light has the properties of both a wave and a particle? file:///C:/Documents%20and%20Settings/todd/Desktop/moire.jpg

ANSWER:
I believe what you are seeing is a moiré pattern which is what you see when you superimpose two or more patterns on top of each other. It is a type of interference on a macroscopic scale, that is, it is not the light which is interfering but the patterns themselves. An example is shown at the right. The fabric satin is pretty because of this kind of effect. You can download some software where you can play around making your own moiré patterns. I guess that I am a little surprised that you can actually see this in this circumstance since I would expect that you would not be able to see the air from the holes as being distinct from the ambient air; maybe it is a different temperature, or contains a little dust, or…? Have you tried to photograph it? I would be interested.

QUESTION:
I teach 5th grade science, and I desperately need a fifth grade answer to this question. I have wonderful bright students who ask excellent questions and I stuggle to answer accurately without completely overwhelming them. "If light is electromagnetic waves caused by the vibrations of atoms or electrons, and if a vacuum is defined as the absence of all matter; then how can light travel in a vacuum?"

ANSWER:
Imagine two magnets in a vacuum. Do they exert forces on each other? The answer is yes as you could prove in your classroom if you have a bell jar to create a vacuum in. What about electric forces? Think about an atom: the nucleus exerts a force on the electrons even though there is a vacuum between the nucleus and electrons. So, both electric and magnetic forces can be transmitted through a vacuum. Physicists often express the presence of forces experienced at some point in space by the existence of something we call a field. If a magnet feels a force it is because it is in a magnetic field; if an electric charge experiences a force, it is because it is in an electric field. Hence, fields can exist in a vacuum. An electromagnetic (EM) wave (like light, radio waves, microwaves, x-rays, etc.) is composed of electric and magnetic fields which are oscillating and move through space with a speed of 186,000 miles/second. A picture of an EM wave is shown above. Think of this as a snapshot; a little later the whole thing will have moved to the right. This is why EM waves have no trouble propogating through a vacuum.

Extra material for the teacher if you think the kids can get it:
If there are fields in a wave, then where are the charges and magnets which cause fields? It turns out that if a magnetic field changes it can cause an electric field (which is how generators work) and if an electric field changes it can cause a magnetic field (which is how electromagnets work). Therefore, if you get a wave going (from an atom or from an antenna), it will keep itself going as it propogates.

QUESTION:
On a sunny day when a sun angle shadow can be measured, and knowing the time of day, how would you calculate the latitude for that position? Also, it you note the sun angle rate of change, dy/dt, can you also determine the longitude by angular displacement or by linear translational velocity? Lastly, if you look at a day/night view of the Earth, the curve appears sinusoidal with respect to the equator. If that's true, then all sun angles on the sunny side should also follow a similar curve. That being said, how would you calculate the longitude/latitude fix of a given sun angle with respect to some other know point along the sinusoidal path?

ANSWER:
In principle, it is simple, just a problem in three-dimensional geometry; you need to know the two angles which specify where the sun is in the sky, the angle of tilt of the earth's axis, and the exact time of year. In practice it is a very complicated process. Nowadays, you could program a computer to take the input data and output the latitude, but I have never heard of this being done since GPS systems make it all so simple. In traditional celestial navigation you wait until the sun is at its highest point, measure the angle, and look up your latitude in a table which is appropriate for the date. Of course, the tables would be in a laptop these days. I do not understand your second question at all. Your third question, the "sinusoidal" day/night boundary, refers to an illusion; the boundary on the globe is a simple circle around the earth and that which you see on a flat map is an artifact of the projection from the sphere.

QUESTION:
An object in motion has kinetic energy. Energy/mass warps spacetime. So as you accelerate, let's say an electron, arbitrarily close to the speed of light (hence its mass/energy increases without bound) ... at what point does its kinetic energy cause gravitational collapse into a blackhole? And couldn't two observers in relative motion each argue with equal validity that its an electron (with respect to its rest frame) or a blackhole (at 99.999 ... 999% c)? Would this imply that were I to chase after and catch up to the electron so that it is now at rest in my reference frame, it somehow undoes its own blackhole formation before my very own relativistic eyes?

ANSWER:
As I have said many times in previous answers I consider the interpretation of special relativity that mass increases with speed to be a good qualitative crutch at best. Your question is one of the best arguments I can think of to support this point of view. Although there are lots of other reasons to consider an electron as an impossible candidate for a black hole, how could it both be and not be one? In its own rest frame the electron would not be a black hole.

QUESTION:
The whole of an electron is negatively charged, what stops the particle blowing itself apart?

ANSWER:
Let's look at something else as an example to put my answer in context. Why does a nucleus, positively charged, not blow itself apart. Because the strong nuclear force, which is attractive for protons/neutrons interacting with protons/neutrons, holds it together. Why does one of the constituent protons not blow itself apart, being positively charged? Because it is composed of fractionally charged quarks which interact with each other via gluons (which is ultimately, the origin of the strong nuclear force. Then why do not the charged quarks blow themselves apart? Because we regard them as fundamental, elementary particles which simply are as they are. I know, that is a very unsatisfying answer, but eventually in science you get down to a point where, until something better comes along, it is simply the best answer. An electron, like a quark, is believed to be a fundamental particle, and is simply indivisible.

QUESTION:
Gravity question. If a bowling ball and a tennis ball are dropped from the same spot they will hit the ground at the same time. So why do I (bowling ball) get to the bottom of a snow covered hill so much faster than my daughter (tennis ball)? We are falling aren't we? Aren't the factors of friction (weight and sliding) balancing with each other?

ANSWER:
This is not an easy question. See my two previous answers.

QUESTION:
Is it possible to describe the motion of a double pendulum as a function of time alone? If so what would this function look like?

ANSWER:
Well, sure but not in terms of mathematical functions you would be familiar with. Even the simple pendulum is easily solvable only for small oscillations. The most useful analytic solutions to such problems involve what are called normal modes; choosing the initial conditions then determines a superposition of these modes. However, the most useful solutions are often computer simulations which are numerical computations of the function which interests you; this is particularly true for large amplitudes of the double pendulum which are chaotic.

QUESTION:
I was curious, if you plugged in the Rydberg Constant, into einstein's equation e=mc2, could you get the smallest theoritical mass of a particle?

ANSWER:
Where would you plug it? The Rydberg constant has the dimensions of 1/length, SI units of m^-1, so it is neither an energy nor a mass. Also, why would you think that there were some generalization here when the quantity is specific to the hydrogen atom? You are also ripe for a physicist's reprimand: physics is not about

QUESTION:
I was wondering about light falling into a black hole. If gravity is pulling light in doest this imply that gravity can accelerate things beyond the speed of light? Or that the force of acceleration of gravity is faster than the speed of light? Have velocity calculations of the x rays and other high energy states leaving black holes? If one were to shine a light beam and an x ray out of a black hole and the light falls bends back in while the x ray escapes, wouldn't this mean that the x ray is technically moving faster than light in that specific state?

ANSWER:
When light is acted on by gravity it does not accelerate like matter does but it does have its energy changed. Light falling into a black hole gains energy so its wavelength gets shorter. But all electromagnetic radiation moves with the same speed in vacuum. And x-rays are no different in this respect. No radiation, regardless of energy, can escape a black hole. And no electromagnetiic wave in a vacuum moves with a speed other than 3 x 10⁸ m/s.

QUESTION:
Lets imagine i have a long stick(please continue reading) thats rounded and as long as the galaxy itself, im holding one side of the stick and the other side is near me, but the stick is a big halo that outlines the galaxy, my question is, if i move the side im holding how long will it take the "move" to reach the other side of the stick, lets say i give 1 step with my stick, how long will it pass until i see the other end moving. I was wondering if that would be faster than the speed of light. I'm here at earth with a stick as long as 4 years light, can i poke instantly somebody by moving this imaginary stick. For the purposes of this the stick wont brake and its light.

ANSWER:
The implications of your question emphasize that it is really unphysical. Suppose we make the halo as light as possible: I reckon that the number of atoms if the halo is a single chain of atoms would be about 10³¹ and the mass would be on the order of 1,000,000 kg. And this would not be very strong would it? Anyhow, the motion at the other side cannot happen faster than the speed of light and it would not even come close to the the speed of light, more like the speed of sound in the halo. I have previously answered a similar question.

QUESTION:
Is there any tangible evidence to Planet X and 2012? If so, why isn't EVERYONE talking about this now? If this thing actually enters our solar system, then we're all history. Is that correct?

ANSWER:
The first thing that comes up on a google search is a site devoted to Nostradamus prophesies. Does this tell you anything about tangible evidence?

QUESTION:
if one were to stand on an infinitely large plane and look off into the distance there would be a horizon. how would one calculate the apparent vertical distance between the lowest point visible and the horizon? As an object moves away from a viewer its apparent size becomes smaller and smaller. If an object were to move away from a viewer at constant velocity what function would designate its apparent size with respect to time?

ANSWER:
A horizon is the line beyond which you cannot see the surface. There is no horizon on an infinitely large plane. An object moving away at constant rate would shrink in apparent size at a constant rate.

QUESTION:
I'm studying Specific Latent Heat at the moment, and I've taken an interest in Plasma outside of school. So I came up with a question, that my teacher couldn't answer. Is there such thing as a Specific Latent Heat Of Plasmarisation? Or something along those lines?

ANSWER:
It takes a certain minimum amount of energy to ionize an atom. You could therefore define some sort of specific heat but I have never heard of anybody doing it. One reason not to do it is that atoms (except hydrogen) can become multiply ionized so that some of the energy you put in would be used to remove even more electrons from already ionized ions rather than to atoms not yet ionized. Melting ice, on the other hand, you use all energy of your latent specific heat to melt, you can't melt it further.

QUESTION:
I have a cylinder which has a piston inside it, 2 inches in diameter. When the end of the cylinder is unrestricted, (a 2 inch opening) it is very easy to draw material into the cylinder and to expell it from the cylinder by moving the pison back and forth. But if the opening of the cylinder is restricted down to 1/2 in diameter, it becomes much harder to draw material in and out of the cylinder. What is the physics behind this?

ANSWER:
Bernoulli's equation is ½ρv²+ρgh+P=constant. Here ρ is the density of the fluid, h the height above some reference, and P the pressure. In this case h is about the same for fluid inside and outside the piston. The pressure outside is atmospheric regardless of what happens inside, so the constant is the same regardless of which opening you use. The half inch opening has an area 16 times smaller than the 2 inch opening, so the velocity will be 16 times greater for the same rate of flow. Therefore ½ρv²+P_2"=½ρ(16v)²+P_½". So P_½"=P_2"-½(255)ρv² so the pressure for the smaller opening must be much lower to move the fluid at the same rate which means you have to pull on the piston much harder. This analysis neglects things like viscosity, compressibility, etc. but gives a reasonable qualitative explanation.

QUESTION:
I have a question relating to an aircraft in flight. Since the total mechanical energy of an aircraft in flight is the sum of it's potential energy and kinetic energy, is the total mechanical energy of the aircraft derived from the fuel source? In other words, does the BTU equivalent of the energy expended by the power plant equate to the total energy of the aircraft? If not, where does the additional energy come from?

ANSWER:
Suppose you suddenly acquired a tailwind. The kinetic energy of your airplane would increase without any additional expenditure of fuel. Also, nearly all the fuel you consume is not used to give energy to the aircraft but rather to make up for the energy lost to air resistance.

QUESTION:
Is there any definitive proof that the rate of radioactive decay of any isotope is constant over the period of Earth's existance?

ANSWER:
The halflife of any particular radioactive nucleus is determined only by the constants of nature. There is absolutely no evidence that there has been any change in the constants of nature over so short a time as the age of the earth.

QUESTION:
Is gravity a form of energy?

ANSWER:
To create energy you need to do work and to do work you need to exert a force over a distance. Gravity is a force so it can do work. For example, drop a ball and it acquires kinetic energy as it falls because of gravity.

QUESTION:
If I have a reservoir filled with water that's 10m deep, 10m long, and 10m wide. And if I have a square hole on the bottom of the reservoir that is 2mx2m in size. And this square hole extends downwards 1m and runs under the reservoir 5m then up vertically 10m to exceed the surface of the reservoir (10m+). What is the initial velocity of the water at the start of the square hole (at -10m)? Also, will the water reach the top (10m+)?

ANSWER:
I make the following assumptions: the fluid is ideal, i.e. laminar flow, incompressible, no viscosity. Then the operative equation is Bernoulli's equation, ½ρv²+ρgh+P=constant. Here, the pressure P is the same at both the surface of the reservoir and the surface in the tube so we may use ½v²+gh=constant; I will choose g to be about 10 m/s² to simplify my arithmetic. Choose h=0 at the bottom of the tank and note that the velocity in the 2 m² tube is 25 times the velocity of the surface of the reservoir. Then ½v²+10 x 10=½(25v)² and so the speed v at the surface of the reservoir is v=0.566 m/s and the speed at the hole is 14.2 m/s. Now, for your second question, we are interested in what the heights of the two surfaces are when the velocities of the surfaces are zero. From the equation ½v²+gh=constant you can see that when the velocities are zero the heights must be equal. The relative heights of the surfaces will depend on the details of the shape of the tube below the reservoir (your descriptions are a bit ambiguous). I estimate that the volume below the bottom of the reservoir is about 31 m³ and so 100h+31+4h=1000, so h=9.32 m. So the fluid will never rise even to the top of the reservoir.

QUESTION:
If you have two tires on a vehicle and they are the same size and ambient temp, is it possible with the front tired at 0psi and the back tire at 35psi to achieve 20psi in the front and 20psi in the rear if you use the 35psi tire to fill the front 0psi tire?

ANSWER:
Provided that the volumes start the same and do not change the final pressure in each will be 17.5 psi.

QUESTION:
I found that the photon have zero rest mass, but when we apply the formula E=m*cc if the rest mass is zero then the E=0. Is there another formula to calculate the energy of a photon?. or E=mc*c only applies to macroscopic objects?

ANSWER:
E=mc² applies only to a particle of mass m at rest; a photon has no mass and is never at rest. The general relation is E=√[m²c⁴+p²c²] where p is the momentum. (See an earlier answer for the definition of relativistic momentum.) So a massless particle has energy E=pc. The energy of a photon is also related to the frequency f of the corresponding electromagnetic wave by E=hf where h is Planck's constant.

QUESTION:
In a vacuum photons travel at it's maximum speed. Then why if they travel that fast based on the formula E=mc*c, why photons don't convert into mass themselves?

ANSWER:
A photon is a stable particle and will not change its identity spontaneously. However, you can induce a photon to create mass. The most common process is called pair production; here a photon, when passing close to a nucleus, will spontaneously turn into an electron and a positron if the photon has more than twice the electron rest mass energy. A positron is the antiparticle of the electron and has the same mass and opposite charge. (See the preceding question for discussion of energy of a photon.)

QUESTION: ;
I can not understand how Heisenberg principle is valid in this case: an EM wave of wavelength L is faling from direction z on a slit d. The photons have p(z)=h/L. So after the slit maximum p(x) = p(y) as it was before the slit. So uncertainty in p(x) is limited to Dp= p(y)-0=h/L. But the slit d can be made as small as desired thus making Dp.d less then h (sufficient is d<L). What is wrong here? Or photons just can't go thru apertures smaller than heir wavelength?

Thank you very much. I am sorry you didnt understand the question and the fault is mine. I really commited an error in writing p(x) = p(y) instead p(x)=p(z). PLEASE TAKE A LOOK AT THIS. I simply mean there is not enough p in the incident beam to satisfy HUP in the case when its wavelength is smaller than the slit. (If the photons dont take impluse from the walls.) Indeed the photons spray after the slit and according HUP [p(x).d>hbar] the component of the impulse parallel to the slit p(x) of at least one photon must be greater than hbar/d. But the photons which are falling have p=hbar/L (L>d wavelength bigger than the slit). What they can do after the slit is to turn to 90 degrees PI/2 maximum. If a photon does so it would have maximum p(x) =p(z)=p=hbar/L Because the impulse must be preserved p(x) can not be greater than p what it had in z direction before the slit (e.g p=hbar/L). But this is smaller than p(x)=hbar/D because L>D.

ANSWER:
The problem is that you are treating a two-dimensional problem as a one-dimensional problem. A vector may be uncertain with respect to either its magnitude or its direction but in one dimension only the magnitude can vary. In the case you describe, the narrower the slit becomes the more uncertain the direction of the photon becomes because of uncertainty in the magnitude of the x-component of the momentum. However, there is still the constraint that the total momentum be unchanged, so the maximum value of p_x is p when the angle with the z-axis is 90⁰. As the slit approaches zero width, the direction of the momentum becomes completely uncertain as required by the uncertainty principle.

QUESTION:
Does a body in the universe at the farthest distance away from the earth exert any real or even theoretical gravitaional or other attractive effect on the earth and vice versa?

ANSWER:
Such force would be so small as to be unmeasurable

FOLLOWUP QUESTION:
Is that the same as non-existent or is it like thediference between .999 repeating and 1.0?

ANSWER:
Theoretically, the force is inversely proportional to the square of the distance, so the force is not zero because the distance is not infinite. However, with distances so vast, we can't really verify this theory by a measurement because of the smallness of the force. Another way to say this is that the laws of gravitation have never been really tested for such huge distances. No good scientist would insist on the correctness of a theory which cannot be tested.

QUESTION:
Compared to the buoyant force of the atmosphere on a 1-liter helium-filled balloon, the buoyant force of the atmosphere on a nearby 1-liter solid iron block is considerally more, considerally less, or the same. My classmante thinks its more because the baloon would displace more space, but i thought it was the same because of the buoyant force law?

ANSWER:
The buoyant force is determined only by the displaced air and a liter of iron displaces the same amount of air as a liter baloon, so both have the same buoyant force on them. But, the iron has much weight greater than the buoyant force so it drops; the baloon has has weight less than the buoyant force so it rises.

QUESTION:
A ship anchored at sea is rocked by waves whose crests are 14 m apart. The waves travel at 7 m/s. How often do the wave crests reach the ship? Using the formula speed=wavelength x frequency the answer would be .5 seconds. Conceptually it seems the answer should be 2 seconds. Can you help explain?

ANSWER:
This sounds like homework, but you seem to already have done the work; plus, you have commendably done one of the most important things in solving a problem which is to ask yourself "does this answer make sense?" You are confusing frequency and period. Frequency is the number of crests per second, and 0.5 s^-1 is the right answer; check your answer for units, though, which should be inverse seconds, not seconds. Period is number of seconds per crest, and 2 s is the right answer. The period is the reciprocal of the frequency, T=1/f.

QUESTION:
Does background microwave radiation or the higgs field provide a means of averaging the energy measured coming from different directions and establish a "special reference frame" that is "at rest" with the background of space?

ANSWER:
First of all, the Higgs field is a hypothesis and never observed, so let's dispense with that. The microwave background would appear to present us with a preferred reference frame and, in fact, it does. However, this is not a violation of the principle of relativity which demands that the laws of physics are the same in all inertial frames: the laws of physics are unchanged in a frame in which the average velocity of the background photons is zero. You could also argue that a preferred frame is one in which the average background photon has a velocity of 20 mi/hr toward the North Star. All the background does is provide a particular inertial frame.

QUESTION:
Why is the speed of light, seemingly arbitrarily limited to 299,792,458 meters per second? More exactly, in being a finite speed, is there anything particular about a photon that makes it travel at this speed in a vacuum, and not another speed, faster or slower? It just strikes me as odd that this has never been explained to me before. I understand that it simply an observation, but is it explained?

ANSWER:
There is absolutely no mystery why the speed of light is a universal constant. Electromagnetic theory predicts waves with a speed determined only by the strengths of the electric and magnetic fields in empty space. An earlier question spells this out in detail. The fact that Maxwell's equations (laws of electricity and magnetism) predict this and Einstein felt strongly that the laws of physics should be the same in all inertial frames is partly what led him to propose the theory of special relativity. Incidentally, the speed of light is exactly the number you quote because the meter is defined as the distance which light in a vacuum travels in 1/299,792,458 seconds.

QUESTION:
If a projectile is shot at high speed from a non-rifled barrel, from the air into the water at an angle, what path does the bullet take through the water? Does any projectile experience a "refraction-like" bending in the water the way a light ray would when moving into an optically denser medium? This question arose when a friend and I were discussing the refraction of light from the perspective of individual photons. I guess the bigger question is: can a strictly particle-view of light explain refraction?

ANSWER:
If you do experiments with particles, you get the wrong result for refraction, that is if the particle slows down it is deflected away from, not toward, the normal to the boundary. So, presumably your bullet would be deflected so as to move more parallel to the surface. If too large an angle of incidence is used, the bullet will skip off the surface, "total internal reflection" except it is really what we would call external reflection in optics. Also, a stream of particles doesn't partly reflect and partly refract, it is either one or the other. Nevertheless, you can still get the right answer if, for photons, you impose the principle of least time: the path taken by the particle (photon) will be that which minimizes the time of flight.

QUESTION:
To my understanding no object can exceed can exceed or even acheive a velo. If an object starting from rest were to have a force exterted on it which would cause it to exhibit an acceleration of 30 km/s*s, according to kinematics after 2.7 hours the object should be traveling at light speed. what would actually happen at this point? does the inertia of the object become infinitely great? continuing to exert a force on this object could cause no change in acceleration. for the action of exterting a force on this object there could be no equal and opposite reaction. does this not violate newton's first law? does this not also violate the law of conservation of energy? If the force exterted on the object over a distance (energy) doesn't go into the acceleration of the object, where does it go?

ANSWER:
(Your first sentence is a little difficult to read; I assume you are referring to the velocity of light.) You cannot use classical kinematics to do this problem because it is incorrect for high speeds. Instead of writing F=m[dv/dt] you must write F=dp/dt where the momentum is defined as p=mv/√[1-(v²/c²)] (not p=mv) where c is the speed of light. If you now exert a force of 3x10⁴ N as you propose (for a 1 kg object), the time to reach speed v is given by t=v/√[1-(v²/c²)]/3x10⁴. So, for example, to reach speed c/2, half the speed of light, it would take, by my calculation, about five and a half years. It would take infinite time to reach the speed of light. When the speed of the particle is large, adding energy by doing work increases the energy of the particle but it changes the speed by almost nothing. (I have always thought that high energy particle accelerators should be called energizers, not accelerators!) You might find the answer to an earlier question interesting regarding why momentum has to be redefined in relativistic mechanics.

QUESTION:
Inertia is a property of mass but is it necc. when moving a mass from rest to apply force or energy exclusively to overcome inertia? In other words, when I begin pushing on a boulder, regardless of friction, won't it remain temporarily motionless in spite of my effort until I overcome the interia? Can that energy be calculated?

ANSWER:
Any force you exert on the boulder will cause the boulder to accelerate unless other forces on it prevent that. You use the phrase "regardless of friction". Do you mean there is no friction? If there is no friction, then that boulder begins accelerating the instant you begin pushing on it; if the mass is very large and your force is modest, the acceleration may be small enough for you to think that it is not accelerating, but it is. However, friction here on earth is never really zero. Here is what happens when you push on the boulder (on level ground):

There is no friction before you begin to push, but when you start to push a little the (static) friction turns on, the net force is zero and there is no acceleration.

As you push harder, so does the friction, so still no accereration.

If you aren't strong enough, you will never be able to move it; for example, maybe the boulder is Mount Everest which you will never be able to budge.

But there is a limit to how big friction can get, and if you are strong enough or the floor is slippery enough eventually it will accelerate since you will now be pushing with a force bigger than the frictional force which is trying to slow it down.

If you stop pushing, the frictional force will cause an acceleration opposite the motion and it will slow down and stop.

When it stops, friction dissappears again.

If the boulder does not move you expend zero energy. If it does, the work you do on the boulder (your force times the distance you push) is equal to the energy expended. Don't forget that friction does work too, negative work since it takes energy away from the boulder.

QUESTION:
WHAT MAKES SCIENTISTS THINK THAT THE FUNDAMENTAL PARTICLES ARE ROUND SHAPED. AS THE STANDAR MODEL SHOW IN ITS GRAPHIC?. WHAT SHAPE DO THEY REALLY HAVE?

ANSWER:
Just because a graphic shows something does not mean it should be taken literally. Now, what do you mean by shape? Shape of the mass distribution? the charge distribution? the current distribution? Physicists measure things called moments which are used to quantify shapes. For example, an electric dipole moment of a neutral particle would imply that there was some positive charge on one side of the particle and an equal amount of negative charge on the other. An electric quadrupole moment of a charged particle would imply a football-shaped (positive moment) or doorknob-shaped (negative moment) charge distribution. The earth is known to have a large monopole moment (it's mainly a sphere), a modest negative quadrupole moment (bulges at the equator), and a small octupole moment (somewhat pear-shaped). Extensive measurements of moments have been made for nuclei but little is known about elementary particles. We really have no means of measuring mass moments which is probably what you think about when you think about the shape of something. It is often assumed, at least for nuclei, that mass distribution usually follows pretty closely the charge distribution.

QUESTION:
Assume that our sun is not a large gaseous sphere but a solid of the same mass. It will attract and hold an atmosphere. What would be the density of the pseudo solar atmosphere at the surface and how thick would such an atmosphere be? Also, considering the refractive index of air on earth, how would the refractive index on this pseudo solar atmosphere vary with altitude?

ANSWER:
This is a pretty complicated question and the answer depends on what assumptions you make in modeling the atmosphere. I will assume that the density of the atmosphere is independent of temperature and that the areal density (the mass above a given area of the "planet") is the same as for the earth. You say that it "will attract and hold an atmosphere". Hold an atmosphere, yes, but it wouldn't attract an atmosphere since space is essentially empty so whatever it has would have to have already been there or to get there somehow. It is fairly easy to show, given the mass of the sun and its radius, that the acceleration due to gravity at the surface would be about g_S=270 m/s² compared to the earth's approximate g_E=10 m/s², about 27 times bigger. If we assume the density ρ of the compressible atmosphere is proportional to the pressure P, ρ=ρ₀P/P₀where P₀ and ρ₀are the pressure and density respectively at the surface of the planet, we find that pressure as a function of height h is P=P₀exp[(-gρ₀/P₀)h]. Because the areal mass density is the same as on earth, one may now show that the pressure and density at the surface are about 27 times greater than on earth. Similarly, the height at which the density would drop to some fraction of what it is on the surface would be 27 times smaller than on earth. The question regarding index of refraction is too technical for this site and depends on assumptions; clearly, the index would be larger than for earth's for my model because the gas is much more dense.

QUESTION:
Consider this scenario - there's a room full of mirrors (for argument's sake let's say all surfaces in the room are 100% reflective). There is a single light source in the ceiling which is sending photons bouncing back and forth off the mirrors. If the light source is switched off one assumes the room will go dark. Why is this the case though? Why don't the photons already emitted from the light source continue to be reflected around the room ad infinitum (i.e. why doesn't the room stay bright)? Why would shutting off the light source affect photons that have already been emitted?

ANSWER:
There is no such thing as a perfect mirror. If there were, you had better not leave the light on too long since the light will continue to increase because there is no loss. When you turn it off, the light would remain bouncing around. Suppose that the mirrors were 99.99% efficient, far better than the best mirror, and the walls were 3 m apart. Then in one millisecond (10^-3 s=0.001 s), the intensity of the light would be reduced to about 1/22,000 of its original intensity! So the real world can impose pretty big constraints on ideal situations we can dream up.

QUESTION:
Why does the front and rear window of my car frost up during winter while the side windows mostly get a bit moist?

ANSWER:
I am not really sure, but I believe that it may be because the side windows are vertical whereas the front and back are not (but the back is in SUVs and vans). This allows them to radiate toward the sky more easily. I know that this is not clear, but I have answered similar questions three times before and if you read those answers (click here and follow the links as you go) you can follow my reasoning in my guess to your question.

QUESTION:
the speed of light is a constant. If i were in a spaceship traveling at half the speed of light, one would think that a beam of light passing by me would appear to me to be moving at half the speed of light, but since the apparent speed of light is an inependent constant time would dilate (slow down) for me in order to maintain an apparent velocity of 300,000 km/s. In essence time has been manipulated in order to maintain an apparent velocity equal to lights absolute velocity. From this i conclude that the speed of light is such a constant that time itself itself will be manipultaed in order to maintain a constant velocity. I happen to know light travels fastest in a vacuum and slower through a medium. do you happen to know how this occurs and why time would not be manipulated (dilated) in order to prevent light from maintaining a constant velocity?

ANSWER:
The constancy of the speed of light results in our having to rethink our ideas of both time and space, not just time as you suggest. But that is not really relevant to your main question concerning the speed of light in a material. The fact that the speed of light is slower than in a vacuum has nothing to do with relativity. I have previously answered a similar question.

QUESTION:
Why are some object transparent? Why do some gases have colour and some don't?

ANSWER:
It all depends on the atomic or molecular structure of the object or gas. Let's take gases as the example. When light shines through a gas it might interact with the atoms. If the energy of the light is just right, a photon might be absorbed by an atom and excite it to an excited state; then, quickly, that excited atom drops back to the original atom and emits a photon of the same energy as the one originally absorbed. But the new photon is radiated in a random direction, so you would see it and the gas would appear to be that color. For example, if yellow light could be absorbed then the gas would look yellow in color. But suppose that there were no states in the atom which could be excited by visible light; then all visible light would pass right through and the gas would be colorless; we would say that this gas is transparent.

QUESTION:
IF GRAVITY IS NEGLIGIBLE AT THE ATOMIC LEVEL, WHY THE GRAVITATIONAL FIELD OF A STAR, FORCE LECTRONS TO FUSE WITH PROTONS, CREATING NEUTRONS? ISN'T THAT A BIG INFLUENCE OF GRAVITY UPON ATOMS?

ANSWER:
When people say that gravity is negligible on the atomic level, they mean that, for example, the gravitational interaction between an electron and a proton if negligible compared to their electrical interaction. When in a sufficiently intense gravitational field, any object with mass will respond. And any atom experiences gravity; that is why the earth's atmosphere does not fly out into space.

QUESTION:
The speed of light moves @ constant velocity & hence is not accelerating. This means that dv/dt = 0. This is the speed limit that nature imposes & nothing can travel any faster. For there to be an acceleration there must be a change in velocity, so if I shoot fireworks into the night sky ( say a Roman candle) & at a later time (dt), I see a flash, hence light. Before the flash occurred, there is only the core material launched & the light didn't exist because the explosion hadn't yet occurred. To me this means the light had an initial velocity = 0. Did the light not have to accerlate from v = 0 to v = constant? I had a change in velocity, hence, the light had to accelerate initially?

ANSWER:
You say that the light did not exist before the explosion. That is the key—it is created already having the speed c. In terms of photons, they are created having a speed c and are absorbed by being annihilated without slowing down. In terms of waves, there is some kind of "antenna" (imagine a charge on a spring) which has both electric and magnetic fields which are time varying and propogate with speed c. (Imagine that a charge is created (as in pair production); the electric field from that charge will appear to an observer a distance d away after t=d/c seconds because fields propogate with speed c.)

QUESTION:
Friends and I are discussing: If a ball is perfectly elastic and it is released over a surface that is also perfectly elastic, and there are no other sources of friction (like air) and no other ways for the ball to lose energy, will the ball continue bouncing forever? Of course these restrictions can never be realized. The question evolved into: Does gravity alone, independent of any other pathways of lost energy like friction, contribute to the successive lower bounces of the ball and the ball's coming to rest? Some are saying that gravity alone contributes to the successive lower bounces; I think this cannot be true.

ANSWER:
Of course, this is a completely hypothetical question, as you note. Let me start on a seemingly unrelated topic: some binary star systems, two stars rotating around each other, are observed to be gradually losing energy for no apparent reason. In the theory of general relativity, accelerating masses will radiate energy much as accelerating electric charges radiate energy in the form of electromagnetic waves (it is how an antenna works). The gravitational radiation is usually referred to as gravitational waves. Gravitational waves have never been directly observed but there is an active program to try to detect them. If you calculate the energy predicted to be radiated by the binary stars referred to above you get a very good match with measured rates, so this provides the best evidence we have so far for gravitational waves (indirect evidence). Your hypothetical ball is constantly accelerating and should therefore radiate energy away and eventually stop bouncing. I don't know how to do the calculation, but I suspect the time for the ball to lose its energy would be extremely long (like you would probably notice no measureable effect in your lifetime or the lifetimes of many generations to come).

QUESTION:
1)IF A PHOTON IS ABSORBED BY AN OBJECT, AND THAT OBJECT EMITS ANOTHER ONE, BOTH PHOTONS WOULD HAVE THE SAME VELOCITY? 2)IF A PHOTON IS ABSORBED BY AN OBJECT AND THAT OBJECT EMITS ANOTHER ONE IT WOULD STILL BE THE SAME PHOTON, OR WILL IT BE THE SAME PHOTON WITH A DIFFRENT FRECUENCY? 3) WHEN ARE TWO PHOTONS THE SAME?

ANSWER:
It makes no sense to talk about a photon being the "same photon" in quantum mechanics. If two photons exist in the same quantum mechanical system, they are identical particles and cannot labeled because their identity can be mixed, that is a particular photon might be 10% of photon A and 90% of photon B. Essentially, your questions are not meaningful in quantum mechanics.

QUESTION:
according to the laws of physics, friction does not depend on surface area. Why then do Formula 1 cars not have narrow tyres and wheels to save weight?

ANSWER:
The so-called "law of physics" is, presumably, f=mN. This is not a law of physics, it is an empirical reltaionship which is approximately true under restricted conditions. Friction is a very complicated thing, not the simple thing normally presented in elementary physics courses. I have previously answered your question, so have a look there.

QUESTION:
Has anyone ever suggested a place for tachyons in the Standard Model or any other model of particle physics?

ANSWER:
I am not aware of any inclusion in the standard model. It is apparently of interest in quantum field theory. See the Wikepedia entry on tachyons.

QUESTION:
The speed of light and gravity. Is the speed of light restricted to the speed at which gravity propergates, if so why? Or is it the case that both gravity and the speed of light is restricted to some other cause like say the speed of the expanding universe or currently where we are in the universe. Further to my previous question, is the speed restriction on the photon caused at the point of where it is released from the atom or is it forced on it all the way along it's journey through space by the fabric of space time itself, or even both?

ANSWER:
The speed of light is a universal constant, it depends neither on the source nor the receiver nor the "fabric of space." The speed of gravity has never been measured but is widely assumed to be equal to the speed of light. See my earlier answer on this question.

QUESTION:
what is RADAR,end howe did worked

ANSWER:
Radar is an acronym and stands for radio detection and ranging. The basic idea is that radio waves are transmitted and when they encounter something they are reflected. If you then detect these reflected waves you can deduce the distance of the reflector by the time of travel, the direction toward the reflector using a directional receiving antenna, and the speed of the reflector by observing the Doppler effect on the detected waves. I would urge you to read the Wikepedia entry on radar.

QUESTION:
what determines how long an electron stays in an excited state?

ANSWER:
The lifetime of a state is determined by something called the matrix element. Essentially this quantity includes the wave functions of the initial and final states and a mathematical object (called the transition operator) which describes the type of transition. Various transitions are allowed for any pair of states characterized by things called multipolarity like electric dipole, magnetic quadrupole, etc. Hence the decay of one state to another generally has many lifetimes corresponding to different multipolarities; one is usually much more probable than all the others, though, and will be the shortest lifetime. The larger the matrix element is the shorter the lifetime.

QUESTION:
Why does a wave with a short wavelength not diffract as much as a wave with a longer wavelength.

ANSWER:
How do you quantify diffraction? What does "diffract as much" mean? Suppose we take, as an example, single-slit diffraction: the longer the wavelength the more spread out is the first maximum in the diffraction pattern. The equation for the location of the first minimum is sinθ=λ/W where λ is the wavelength and W is the width of the slit. So the angular width is approximately 2λ/W. Since this is proportional to the wavelength, longer wavelength is more spread out. You can see this at this site.

QUESTION:
Based on the principal of binding energy when we burn fossil fuels we are reducing the net mass of the earth. So how much mass has the earth lost from burning fossil fuels (coal, oil, and natural gas) in the last 100 hundred years.

ANSWER:
Assuming that the released energy does not escape from the earth, the total mass of the earth does not change; this is because of conservation of energy of an isolated system.

QUESTION:
My 8 year old asked me if gravity has the same effect on water vapor as for everything else. I thought this an interesting question and wondered about the effect of heat on gases and what about mass? I thought that mass was not a factor in gravity's effect.

ANSWER:
Gravity has exactly the same effect on any object: the object experiences a force which is proportional to its mass. This force is called the weight of the object. So, yes, gravity affects water vapor molecule by molecule. If there were no gravitational force on water vapor, when water evaporated it would simply fly out into space and all water would have been long gone by now. By the way, that is why there is no evident water on the moon—the gravity there is not strong enough to hold its atmosphere. Keep in mind that weight is seldom the only force on an object. Consider a dust mote; it appears to float around weightlessly but it is experiencing forces from the air it is in which keep it from dropping the same way a bowling ball would.

QUESTION:
I want to know what is the force behind electrons in a moving circuit. I want to know what makes them move. Explain what potential difference is.

ANSWER:
The potential difference between the ends of the wire causes there to be an electric field inside the wire. This field exerts a force on the electrons which then move. If there is a potential difference between two points in space this simply means that a charged particle between those points will experience a force. Positive charges will experience a force towards lower potential and electrons will experience a force towards higher potential. Potential is related to potential energy of a charge in a field. If the potential energy of a charge Q is U then the potential at that point is V=U/Q.

QUESTION:
This is a question about why optical fibers are designed the way they are. I know that an optical fiber has a center core of glass with a high index of refraction which carries the light signal. There is an outer cladding of transparent material around the core which has a lower index of refraction than the core. The light signal is confined to the core because it reflects off the interface between the core and outer cladding due to the difference in index of refraction. My question is this: why don't they simply use a single glass fiber with a uniform index of refraction and coat the outside of the fiber with mirror silvering so that the light signal is confined to the inside to the fiber by mirror reflection? In other words, why is the index of refraction interface better for confining the light than a mirror surface?

ANSWER:
The kind of reflection which occurs in fiber optics is 100% efficient, that is no light is lost. It is called total internal reflection and occurs when a boundary with another medium with smaller index of refraction is encountered at an angle greater than the critical angle. In principle, one could just have a glass fiber in air which has an index of refraction smaller than glass; the sheathing is just for uniformity. A mirror, on the other hand, is not very efficient, maybe only something like 90%. 90% sounds good, but when you think of the millions of reflections the light undergoes, you quickly end up with almost nothing—0.9^1,000,000≈0.

QUESTION:
is it considered possible that space has a structure , Iv;e read (popular magazines and science channel) that some physicists believe that it is like a lattice , foam, or granular fluid and if so could it flow like a fluid? what do they theorize it might be composed of ?

ANSWER:
You are essentially asking whether space is quantized. I have previously answered this question; the answer involves what is called the Planck length. It is certainly not possible with present knowledge to prove that space is discretized.

QUESTION:
I would like to know what causes a charge at the atomic level. I know that if you were to have more electrons than protons then you would have a negative charge. Or even at a more basic level what causes quarks to have fractions of a charge? What causes an electron to have a negative charge?

ANSWER:
See the answer below. Electrons and protons have equal but opposite charges. The electron's charge being negative is a arbitrary; it simply must be opposite that of the proton.

QUESTION:
If electromagnetism is conveyed by photons, why is electricity considered a flow of electrons? Why isn't it a flow of photons?

ANSWER:
The photon, as you correctly state, is the conveyer of the force. Electric current, by definintion, is the flow of charge and photons have no charge. Some signals are conveyed by flow of photons: when pulses are sent down a fiber optic cable it is light which carries the information much as electrons do in a copper cable. Come to think of it, light from a light bulb is a flow of photons.

QUESTION:
Hello, I'm a high school student and I have a few questions which are probably very annoying. For most of these things I have only been able to get circular or abstract meanings which don't explain HOW and WHY these things occur. Here's one of them: 1) What is charge actually? (not just when it's said that an atom is charged because it has more positive/negative protons/neutrons etc., but also the charge that forms electric fields. In other words what exactly are coulombs measuring, and what DOES and electric current consist of?). Thankyou!

ANSWER:
The problem often is that people don't know what physics is. In many instances, particularly at the foundations, we are compelled to be empirical, to simply acknowledge that some things are because they are. We begin doing physics by looking around at forces in nature. We feel our own weight, the force the earth exerts on us because we have mass and, through many experiments and calculations, we discover that two objects that have mass exert forces on each other. But we don't really know what mass is, do we? It is a property that most things in the universe have which allows them to exert and feel gravitational forces. That may be unsatisfying to you, but sometimes it is the best science can do. Armed with our experience studying gravity, maybe we now look around for other kinds of forces in nature. One day when combing our hair we notice that there seems to be a mysterious force which attracts our hair to the comb, seemingly having nothing to do with gravity. We start doing experiments and make a remarkable discovery—some objects in the universe possess a new property which we decide to call electric charge which allows them to cause and feel this new force which we call the electromagnetic interaction. It is a force much stronger than gravity and may be either attractive like gravity always is or repulsive; hence we conclude that there are two different kinds of charge whereas there is only one kind of mass. But what actually is charge? We really don't know, we simply infer its existence by observing nature.

QUESTION:
ordinarily, in order to find the electrical current through a conductive medium one can utilize Ohm's equation and simply divide the electric potential by the overall resistance of the medium through which the electricity travels, but if one were to attempt to find the electrical current through a superconductive medium by using Ohm's law one would have to divide the electric potential by an overall resiatnce of zero, making the electrical current, In theory, infinite. I know in actuality this can't be the case. How would one find the electrical current through a superconductive medium if Ohm's law is not applicable?

ANSWER:
Ohm's law is not really what I would call a law because it is something only approximately true for only some materials. So, technically, Ohm's law will not tell exactly what the current is in anything. In a super conductor imagine you get 10 amperes of current flowing; it will continue to flow forever dependent on nothing and so you would have to simply say the "law" is I=10 for this situation. Now go in and increase the current to 20 amperes; now the "law" is I=20. How can you cause a current to flow? Just momentarily attach to a battery or use a changing magnetic field to cause an induced current.

QUESTION:
I am a high school student, currently having a debate with my friends about existence of "coldness" As an active pursuer of philosophy, I was taught that there is no such thing as "cold" - It is only the absence of heat. However, as my knowledge extends only so far, I have no confidence nor proper knowledge to effectively pursue my friends of this simple concept when the debate turns into a science debate. So I ask you, if, scientifically, "cold" is merely a word to describe the absence of heat (or the movement of molecules, for that matter)

ANSWER:
Hot, cold, warm, cool, tepid, lukewarm, scalding, icy,… These are all qualitative words which give us qualitative information about the temperature of something. So, the pertinent question is: what does temperature measure. In physics, temperature is a measure of the average kinetic energy per molecule of the object. (Kinetic energy of a mass m with a speed v is ½mv².) This is actually what temperature is for a gas; for a solid it is a little more complicated but essentially comes down to average energy per molecule. So, when we say one object is colder than another it does not mean that it has more of something called coldness as suggested by your friends; rather it means that it has less internal energy per molecule, the molecules are jostling around with less speed than something not so cold. Incidentally, your use of the word heat is incorrect; but don't feel badly because lots of physicists use it incorrectly too. Heat (Q) should be reserved for energy which is transferred from one object to another whereas the temperature of something is determined by its internal energy (U). The first law of thermodynamics is essentially energy conservation. The change in internal energy of a system equals the heat which flows into the system plus the work W done on the system, ∆U=∆Q+W.

QUESTION:
Some 30 years ago I took an electronics course and there was an ongoing debate over the amount of time it took from when power was first applied to a circuit to when it was available throughout the circuit. Some said it was instantaneous, while others argued the point. I was never fully sure if what they really meant was "relatively instantaneous" (as in the speed of light), because for all practical purposes there would be no effective difference in most circuits. Do you have an answer?

ANSWER:
Hell, I have an answer for anything; I might not be right though, my wife tells me. When you switch on a light it comes on instantaneously. Or, does it? As you probably know, the drift speed of the electrons which flow in the circuit are very small, much smaller than a millimeter per second. However, that which moves the electrons is an electric field in the wire and when you turn on the switch, the field appears in the wire at the speed of light, so it is not really instantaneous, but since the speed is so large, it is for most practical purposes. There are other effects which make more noticible delays. When a current starts flowing in a loop, a magnetic field starts building up and this changing field causes a back emf around the circuit which opposes the increase of current; this is Lenz's law. Another way of saying this is that the self inductance of the circuit will keep the current from changing too fast. So if you had a simple circuit with a resistor, a battery, and a switch and you watched the voltage across the resistor with an oscilloscope when you closed the switch, you would see a time much longer than the speed-of-light time.

QUESTION:
Is there any study or theory to explain the electrical charge of an electron as a internal way of motion of the electron?

ANSWER:
No.

QUESTION:
If the rear wheel of a a 3/4 ton car, moving at 10mph, drove over someone's ankle, would that person be able to get up and walk away withiout a bruise, a mark or injury of any kind?

ANSWER:
I am not a forensic expert, so my opinion should hold no sway from a legal perspective. This could certainly happen if either the tire or the ground were soft. Also, if the victim were wearing a shoe with a relatively strong sole which could support the weight of the car momentarily.

QUESTION:
I did the following experiment: I parked one car on my driveway. I parked the other car in the garage but left the garage door WIDE OPEN. Overnight, the temperature dropped below the dew point. The garage walls are insulated but the ceiling is not. The garage is not heated. Result: Frost formed on the windows of the car on the driveway but not in the garage. I assume that the temperature inside and outside both cars was the same overnight so why did frost form on the windows of the car in the driveway but NOT on the car in the garage?

ANSWER:
I have answered similar questions twice before. There are two important factors in frost formation at temperatures near the freezing point, radiation cooling and evaporative cooling. My research has led me to believe that radiation cooling is more important. If you read my earlier answers, which are much more exhaustive than this answer, you will see that all things radiate away energy and that tends to cool them. However, there are also many things in the environment which are also radiating energy and this energy will be absorbed by its neighbors, and so everything will tend to be in thermal equilibrium. So, look at the car in the garage: it, the walls, and the roof are all at, say, 34⁰ and radiating but also absorbing so all stays at 34⁰ and no frost forms. Now look at the car outside: its environment is at 34⁰ and it is radiating accordingly but it does not have the walls and roof from which to absorb energy and so it cools to a lower temperature and frost forms. The second factor is evaporative cooling. As you probably know, since it takes energy to evaporate water, evaporation cools; just take a damp rag and twirl it around and you will see that it gets cold. If there is a breeze which would hasten evaporation and the car in the garage is sheltered from the breeze, this would again give the outside car the cooling advantage. I have noticed this effect even if one car is parked in the vicinity of a house and the second is not.

QUESTION:
two walls stand opposite each other. The length between them is L. one of the walls is moving toward the other at velocity V a bird sits on that wall starts to fly back and forth at velocity 2V how far will the bird travel before it gets crushed (assume the bird has no dimension and that only when the walls meet will the bird be crushed)

ANSWER:
This is a trick question, much easier than it seems. The walls will smash together at the time T=L/v and during that time the bird will fly a distance S=2vT=2L. OK, I will admit it—I spent some time trying to compute the infinite series before I figured this out! But it was kind of cool because I was able to use simple logic to find that the infinite series from n=1 to n=∞ of (1/3)ⁿ is 1/2 which I could not do mathematically because I am not very good at evaluating infinite series.

QUESTION:
Are all coupling constants dimensionless and is this a strict requirement?

ANSWER:
This is mainly a case of semantics. A coupling constant is something which tells the strength of an interaction; for example, electric charge could be thought of as a coupling constant for electrostatics or mass as a coupling constant for gravitational forces. However, field theorists prefer to work with quantities which do not depend upon the system of measurement and so coupling constants are usually defined in such a way that the constant is dimensionless.

QUESTION:
Thank you in being available for this type of thing. I chat at physorg and I learn alot, but there are some cranks who state things of opinion as fact. Please laugh at this question! A member of physorg is adament that the neutron is the force carrier for gravity. Myself and 2 or 3 others are trying to explain why and how that can't be and why the graviton fits with our current knowledge, but he continues to claim he is correct. Could you please come up with one statement of why this is impossible so that I can quote it to him. There must be a perfectly clear answer that even he has to recognize as fact, yes?

ANSWER:
The current theory of gravity, general relativity, attributes the gravitational force to geometric effects, the warping of space-time by the presence of mass. There is no successful theory of quantum gravity, that is the field has not been successfully quantized thereby allowing identification of the "force carrier". There is no such thing as a graviton, it is only a qualitative idea at this time. So, your nemesis thinks maybe the neutron is the graviton, right? Here is what is wrong with that:

To the best of our knowledge, the gravitational force propogates with the speed of light. The neutron, being a particle with mass, cannot travel the speed of light. In fact neutrons, having no charge, are quite difficult to accelerate and are usually relatively slow in nature.
The neutron is not a stable particle unless it is bound inside a nucleus; a free neutron has a lifetime on the order of 15 minutes at which time it will decay into a proton, and electron, and an antineutrino. This would not be very good for communication of the gravitational force between, say, the sun and Jupitor would it?
Forces which have carriers with mass, for example the strong nuclear interaction with mesons as field quanta, are very short ranged. Gravity is a long-range interaction like electromagnetism, that is it falls off like 1/r². The force carrier for electromagnetism is the photon which is massless and one would therefore expect the graviton to be massless.

QUESTION:
is energy quantized ?

ANSWER:
If a system is bound, its possible energy states are discrete or quantized. If a system is unbound, its possible energy states are continuous (not quantized).

QUESTION:
Sorry in advance for what may be a overly simple question; but after watching various lectures on particle physics I was wondering is there an actual proton, or is a 'proton' now verbal shorthand for the two up & one down quarks which make up a proton? Or in other words, after you remove (theoretically of course) the three quarks which define a proton, is there anything left?

ANSWER:
This is just a matter of semantics, isn't it? Would you say that there is no "actual" hydrogen atom because we know it to be composed of an electron and a proton?

QUESTION:
Are power density and specific power the same thing? I know power is work per unit time. Seems they would have different units--power density--power per volume and specific power -power per unit mass. The same for energy density and specific energy.

ANSWER:
I never heard of power density or specific power. It turns out, according to Wikepedia, that they are engineering terms and are apparently synonymous, both meaning power per unit mass. In physics energy density is energy per unit volume. Specific energy is apparently energy per unit mass but I have not seen this quantity used in physics except in the context of specific heat.

QUESTION:
Is there (potentially or actually) light in the universe we cannot or potentially cannot DETECT (or see visually) on our color spectrum systems? Does all light in the spectrum we know about/see, travel at the same speed: light speed?

ANSWER:
By definition, light is the portion of the electromagnetic spectrum to which our eyes are sensitive. It is a tiny part of the whole spectrum which includes also radio waves, ultraviolet radiation, xrays, gamma rays from nuclei, infrared waves, etc. All electromagnetic radiation travels with the same speed in vacuum.

QUESTION:
how law of conservation of energy is not voilated in step up & step down transformer

ANSWER:
Because it is not the law of conservation of voltage. You may not draw more energy from a transformer than you put in. Since the power is VI, the power input VI must equal the power output VI. For example if you have a transformer which has a step up factor of 10, you may only have a current 1/10 of the current supplied to the primary. (Your email address is not valid.)

QUESTION:
Does a kernel of popped popcorn have the same number of calories as it had before it was popped? Do not consider that it is fried in butter, or that tiny particles of the popcorn fly off when it is popped. My friend suggests that it uses energy (calories!) in the popping process, I believe it simply is releasing energy it has received in the heating process, which cause moisture in the kernel to turn to steam, expanding, and creating the "popping". Do total calories remain the same before and after?

ANSWER:
The first thing we should acknowledge is that what "cooking" does is change the chemical composition of whatever you are cooking, and changing the chemistry inevitably changes the caloric content. That said, let's examine what happens when you "cook" popcorn. The water inside the kernel becomes superheated and the hull cannot contain the increased pressure and the kernel explodes. When this happens the starch contained in the kernel expands rapidly which is what the popcorn is. The rapid expansion causes cooling which tends to keep the starch from undergoing a chemical change, and therefore popping corn is, to a large extent, not really cooking. So, in my judgment, you are correct: the caloric content is not much changed by the popping.

QUESTION:
Can you please explain electron spin? It does not seem to fit in with the model I have been taught of a cloud of electrons 'orbiting' a central nucleus.

ANSWER:
The earth orbits around the sun. Therefore the earth has an angular momentum called orbital angular momentum. The earth rotates about its own axis. Therefore the earth has an additional angular momentum which we could call spin angular momuntum. The spin angular momentum has nothing to do with the orbital angular momentum.

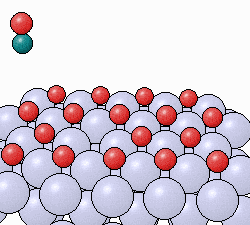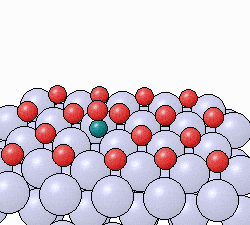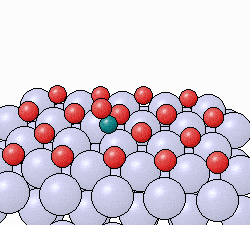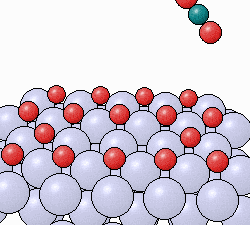
An electron orbits around the nucleus (or, more sophiscatedly has a wave function which contains the information about the electron cloud). The electron has an angular momentum called orbital angular momentum, the information about which is also contained in its wave function. Like the earth, the electron has an additional intrinsic angular momentum which we call spin angular momuntum. It is as if the electron were spinning on its own axis (although that classical idea has problems if taken too literally). The spin angular momentum has nothing to do with the orbital angular momentum (or the electron cloud).

QUESTION:
How to derive E=m.c.c?

ANSWER:
You should be able to easily find this in any physics text. I have outlined the derivation in an earlier answer. You basically calculate the amount of work necessary to speed an object of mass m up to a speed v and call that the kinetic energy.

QUESTION:
For a non-scientific person, what would be an explanation of the term "array" when used in discussions regarding lasers? (i.e. medical lasers or ipl)

ANSWER:
This simply means a bunch of something. Array usually implies that they are arranged in an orderly way.

QUESTION:
the situation is this you use the elevator in the mall and you put a weighing scale inside the elevator you measure your weight and mass due to explain the second law of motion. is there changes in your weight as you go up as you go down?. if there changes, what is the reason of it changes. what is the scientific principle of it?

ANSWER:
Your mass is a measure of how much matter there is in you. Being in an accelerating elevator cannot change that. Your weight is the force which the earth exerts on you. Being in an accelerating elevator cannot change that. What changes is your apparent weight, how heavy you feel. You can determine this by looking at a scale on which you are standing; this scale does not really measure your weight but rather the force with which you push down on it. If you are accelerating, Newton's second law says that the net force on you will not be zero and the only forces on you are the scale (up) and you weight (down). [Keep in mind that the force the scale exerts up on you is equal and opposite to the force you exert down on it because of Newton's third law.] If you are accelerating up (either going up speeding up or going down slowing down) you will feel heavier. If you are accelerating down (either going down speeding up or going up slowing down) you will feel lighter.

QUESTION:
How close are scientist to developing a super laser similar to the weapon used in the death star in star wars or is it even possible to develop such a weapon. If it is no t possible to make a laser like that then what is some of the weaknesses of this model and please explain why it cannot be done if possible.

ANSWER:
Nobody is even considering trying to develop such a weapon. The reason is very simple—we do not have access to the amount of energy it would take to operate it. If you were to totally blow apart an earth-sized planet the total energy you would have to supply is about 10³² J; to calculate this, just use the magnitude of the total gravitational potential energy of a uniform sphere is, 3GM²/(5R). Now, the death star took about one second to blow up the planet, so the power had to be 10³² W=10²⁶ MW. The entire power output of the US is about 10⁶ MW, about a million megawatts. So it takes a mere 10²⁰ Americas delivering all their energy in a second to fuel the death star laser.

QUESTION:
Eart pulls the yo-yo downward and the yo-yo pulls earth upward.Which of Newtons laws explains this?

ANSWER:
The third.

QUESTION:
What happens tp particles at 0K?

ANSWER:
It cannot happen, quantum mechanics forbids it. You can extrapolate from nonzero temperatures and conclude that all the molecules would be at rest, but you can never really get there because the Heisenberg uncertainty principle says that you cannot know the velocity exactly if you have any knowledge at all of the position of the particles.

QUESTION:
If light beams bend in the presence of mass, then, if we view the entire universe as a pretty large mass, then all light beams must be bending. That means that 2 light beams departing an object in different directions might eventually cross each other's path (might take a few billion years but might happen). Is it possible, therefore, that, when we look up into the sky, we might be seeing the same object more than once - as x light-years away in one direction and y light-years away in another? If we see this object at very different ages then there might be no way to determine that we are, in fact, looking at the same thing.

ANSWER:
In fact this has been observed many times in an effect called gravitational lensing. If, between us and a distant galaxy, there is a very massive and compact object, light passing to the right and to the left will both be bent, for example. In that case we will see two images of the same galaxy. More commonly, one just sees blurs or streaks of light from the source. Some nice images may be seen here. Your hypothesis that something could have images at very different times because of very different path lengths is unlikely since the intensity of the earlier image would be hugely reduced because of the much longer distance the light had to travel.

QUESTION:
What is the definition of a megarod (pertaining to radiation)?

ANSWER:
I think you must mean megarad. One rad is the amount of radiation which will deposit 0.01 J of energy in 1 kg of material. So, you see, a different amount of radiation will be 1 rad for steel than for human flesh. A megarad would be 10⁶ rad. Incidentally, the rad is an obsolete unit and radiation doses are now more often quoted in Grays (Gy) where 1 Gy=100 rad.

QUESTION:
Does the orbital velocity of a meteoroid at the Earth's distance from the Sun (in space) depend upon the eccentricity and size of the meteoroid stream? Are the speeds of meteors from meteor showers the result of two vectors: the Earth's orbital velocity and the meteoroid's orbital velocity?

ANSWER:
I really do not understand what the first part of your question is asking. Certainly the velocity of any object in orbit around the sun depends on the orbit and where the object is on that orbit. If we view the velocity of a meteoroid on the earth, then the velocity we see will be the the velocity of the meteoroid relative to the sun minus the velocity of the earth with respect to the sun, v_ME=v_MS+v_SE=v_MS-v_ES where, for example, v_MS is the velocity of the Meteoroid relative to the Earth. This ignores the fact that we also have a velocity due to the earth's rotation about its axis.

QUESTION:
is it possible to prove that there is a mimimum size X and nothing can be smaller than X ? I seem to recall this may be Planks constant. A similar analogy is there is a maximum speed ie C and nothing can go faster than C

QUESTION:
What is gravity at the sub-atomic level

ANSWER:
Negligible.

QUESTION:
I assume the earth performs work in keeping the moon within its orbit about the earth, otherwise the moon would just fly off into space. As it performs work is expends energy. Further I assume there is a minimum size that something can be as everything is composed of waves. The smaller something is the smaller the wave the shorter the wavelength. Wavelength is proportional to the energy the wave contains. If a wave has infinitely small wavelength then it has infinite energy within a finite volume and therefore infinite energy density. As energy density is proportional to an objects gravity infinite energy density means infinite gravity. From the above I conclude that gravity does not expand out into space for an infinite distance as the amount of work done by the earths gravitational field on a planet billions of light years from earth would be so small that it would be smaller than the minimum sized object…is this right?

ANSWER:
Consider a book sitting on your desk; since it does not fly off into space the earth must be doing work on it, right? Wrong. Just because one object is bound to another does not mean work is being done on it. So, first examine the moon situation: let's start out making the approximations that the moon's mass is negligible compared to the earth's and that the moon's orbit is circular; these are both approximately true. Then, since the moon's velocity is always perpendicular to the gravitational force it feels, no work is done. Hence, to an excellent approximation, the earth does no work on the moon. Now the more general case: If the moon's orbit is such that the moon is getting closer to the earth, the earth is doing positive work on the moon and if the moon is getting farther away, the earth is doing negative work. But, the moon exerts a gravitational force on the earth which is exactly the same magnitude as the force which the earth exerts on the moon but in the opposite direction (Newton's third law); therefore the moon is always doing work on the earth which is just the negative of the work which the earth does on the moon, so the net work done by the earth-moon system is zero, that is the total energy of the system does not change.

Your statements regarding wavelengths of particles are incorrect. A bowling ball going 100 mi/hr has a much shorter wavelength than an electron going the same speed. Wavelength is not determined by size of the particle.

I have no idea what you are trying to say about infinite gravity etc., but it probably doesn't matter because it seems to be based on your ideas of wavelength.

QUESTION:
If you are using a laser to cool an atom, the momentum of a collection of photons is used to in a way counteract that of the atom. So if you have an atom moving towards the right, it hits a photon traveling towards the left, tuned to the resonance frequency of that atom and hence is more likely to be absorbed. The tiny amount of momentum that the photon has is transferred to the atom in the opposite direction to the direction of travel and hence slows the atom down. However what i would like to know, is that once the atom has absorbed the photon, it cannot stay in that excited state forever, so surely eventually it must emit another photon in a direction which is totally random i believe. As the photon is emitted will it not give the atom a slight kick in another direction? Considering the direction of emission is totally random i would like to know why laser cooling is still so effective at cooling atoms.

ANSWER:
A thousand small kicks opposite the direction the atom is moving will make a significant change in the speed of the atom. A thousand small kicks in random directions will average out to just about zero change in the speed of the atom.

QUESTION:
Is gravity a byproduct of electromagnetism or somehow related to it.

ANSWER:
Nobody has ever successfully unified electromagnetism and gravity; there is no known relation between the two. Interestingly, Einstein, after completing the theory of general relativity (which is our best theory of gravity) in 1916, spent the rest of his life (he died in 1955) trying to develop a unified field theory which would unite the two forces but with no success.

QUESTION:
Hello, I would like to know how much time passes on earth, doing one light year. The reason I'm asking this question, years ago, I read an article about traveling to the Andromeda Galaxy from earth at the speed of light and return. The article said the earth would 300 million years older when you return. I seen other articles on the internet suggesting 2, 4, and even 20 million year would pass. So what would be the correct time passage on earth? Could you also tell me in layman terms, how you came up with the anwer, Thanks!

ANSWER:
For starters, your terminology needs some touching up: a light year is a distance, not a time; it is the distance light will travel in one year. Second, no material object may go the speed of light, so your question technically has no answer. Now, Andromena galaxy is about 2.5 million light years from earth. Now, let's assume that the spaceship is going 0.99999 the speed of light. Then from earth's perspective it will take almost exactly 5 million years for the round trip so the earth will be that much older. The ship, however, will see the distance to be only 2.5√(1-.99999²)=0.011 million light years=11,000 light years so the time for the trip as measured by clocks on the ship would be about 22,000 years.

QUESTION:
If you had 2 trains traveling side by side Train A. at top speed and Tran B. at half of that speed. As the two trains are traveling along Train B. is ahead of Train A. but as Ta is about to pass Tb at the exact moment they are exactly side by side lightning strikes 1000meters ahead of them. Considering the fact that time slows down the faster you travel, which Train driver would see the lightning strike first? i believe if it was possibale to measure, the Train driver travelling slower (Train B.) would see the light first. This is similar to einsteins thought experiment.

ANSWER:
I believe the key here is length contraction. A train with speed v will measure the distance to the light source not as 1000 m but as L=1000√(1-(v²/c²)) where c is the speed of light. He will see the light approach him with speed c regardless of what v is (the basic postulate of special relativity) and, while the light approaches him he is approaching to meet it. So, calling t the time (measured by the train) until the light is seen, we can write ct=L-vt. Doing a little algebra, you will find that t=(1000/c)√[(c-v)/(c+v)]. Note that the larger v is, the smaller t is; so, as measured by the clocks on the trains, the faster train sees the light first.

QUESTION:
Please explain why a magnet does not drop straight through a copper tube.

ANSWER:
The magnetic field of the magnet moves with it so the magnetic field experienced by the copper is changing with time as the magnet drops. However, Faraday's Law states that a time varying magnetic field will induce an electric field and this electric field will cause an electric current to flow in the copper. This electric current will have an associated magnetic field which will exert force on the magnet.

QUESTION:
Does gravity cause an elrctron to orbit

ANSWER:
No. The orbit is caused by the electric force. Gravity is totally negligible on the atomic level. I have previously answered a similar question.

QUESTION:
how does the magnatism of the sun and the magnatism of the earth affect the earths orbit ?

ANSWER:
In no measurable way. Magnetism is totally negligible here.

QUESTION:
does Atmospheric pressure effect ones weight on a plant.

ANSWER:
The atmosphere does not affect weight since weight is the force of attraction to the earth. However, one's apparent weight is affected because there is an upward buoyant force which adds to the weight force to make the weight appear less; for example, a helium balloon has a greater buoyant force than weight and so it appears to have negative weight. A more thorough discussion of this may be seen in an earlier answer.

QUESTION:
If an object is traveling east with a decreasing speed the direction of the objects acceleration is: 1-North 2- south, 3 east. 4- west? My grandson was given this question in a physics work book the answer the teacher gave was 4-West. I believe the answer to be 3-east. I believe the book for H.S. students is trying to give one familiarity with the definition of acceleration which is a change in velocity and or direction. Since the object is slowing down (constant speed) it is accelerating ie its velocity changed ie in the negative. I know that velocity and acceleration are vectors and that speed is not etc.amI correct ie it accelerates in the direction it is going east but is negative. I understand that Physicists do no like to use the word decceleration.Kindly help since my grandson and I have differing opinions.The teacher is a biologist who is also teaching physics. There is no disrespect but simply I want to know since I am quite interested in this.

ANSWER:
What you are saying is incorrect, the teacher's answer is correct. An object speeding up has an acceleration vector in the direction of the velocity vector; an object slowing down has an acceleration vector opposite the direction of the velocity vector. The negative sign which your argument deduces is correct and means that the vector representing the change in velocity, which is tells the direction of the acceleration, is opposite the velocity.

QUESTION:
I've used this: "all energy will go from high to low spontaneously" as a rule-of-thumb definition when explaining events in the context of the Second Law of Thermodynamics. I haven't found a shorter or simpler explanation, but now I've been told that my rule-of-thumb definition is wrong. I don't think it is wrong and the person who told me it was wrong is not a physicist, but perhaps you could show me where it is wrong? And, if it is wrong, could you give me a short and simple rule-of-thumb definition that I could replace it with?

ANSWER:
You have to be careful when you throw around the word energy. Also, your definition does not state high or low what. If you mean that "heat cannot spontaneously flow from a material at lower temperature to a material at higher temperature", then your statement of the second law is correct.

QUESTION:
As a non-scientist doing primary science teaching - I have a problem and I can't work out the answer. Doing stuff using a toy car on a ramp, it seems that the heavier the vehicle, the faster it is going at the bottom and consequently the farther it goes at the end of the ramp. My gut reaction is that the heavier vehicles have better axle construction, so less friction - and it is this not their mass that causes the difference. I have done maths and know about KE and PE and I cannot see how the extra mass would in fact increase the velocity, although the momentum would be greater - am I correct or am I missing something?

ANSWER:
Well, this is very interesting. A recent question was very similar except that experiment had just the opposite result, the lighter car went faster! I can only reiterate that, in simplest physics, with no friction all cars will reach the bottom at the same time. This is also the result if there is friction but the friction is proportional to the weight (as in the usual f=µN for sliding friction where N is usually proportional to W). So, your gut reaction is right—the result of the experiment must indicate that the friction of the winner is smaller (relative to the weight).

QUESTION:
A ball rebounds one-half the height from which it was dropped. The ball is dropping from a height of 160 feet and keeps on bouncing. What is the total vertical distance the ball will travel from the moment it is dropped to the moment it hits the floor for the fifth time?

ANSWER:
This is really not physics, it is math. Until it hits the first time it goes 160 ft; until the second time, 2x(1/2)x160 ft; until the third time 2x(1/4)x160 ft; etc. So the total distance would be 160+2x(1/2)x160+2x(1/4)x160+2x(1/8)x160+2x(1/16)x160=160x[1+2x(1/2+1/4+1/8+1/16)]=460 ft.

QUESTION:
I'm wondering about the distances between subatomic particals and that relationship to their size. If the subatomic particals of all atoms on the Earth, for example, were to collapse to the point of actually touching each other, what would be its diameter?

ANSWER:
First of all, subatomic particles do not have well-defined sizes (they are sort of smeared out over space) so "touching" each other does not really have a definite meaning. However, if we suppose the protons and neutrons in a nucleus are just touching, we can compress the whole earth so that its density becomes that of nuclear matter (the mass of a typical nucleus divided by its volume) and see how big it is. The density of nuclear matter is about 10¹⁸ kg/m³ and the mass of the earth is about 6x10²⁴ kg. So the volume of the earth compressed to nuclear matter density would be about 6x10⁶ m³. This would correspond to a radius of about 113 m, pretty small! Incidentally, this is what happens to a star when a neutron star forms in stellar evolution.

QUESTION:
me and my friend have been arguing about this for a week and he refuses to accept defeat unless i get a "credible" source. So here goes: We were talking about mars has approximately a third of the gravity that earth does, and he said that is because the ATMOSPHERE is thinner there and it wouldnt be a third if mars had an atmosphere similar to Earths. This turned into a debate with him claiming that the atmosphere has everything to do with gravity and your weight, how do I explain in a way that makes sense that gravity is entirely about the mass of a planet and not atmosphere? He says that even if i were right, if the earth all of a sudden had no atmosphere whatsoever we would all weigh less because there would be less total mass around our planet. Please help!

ANSWER:
You are correct that the mass of the atmosphere is negligibly small compared to the mass of the earth, however that is not the reason why gravity at the earth's surface is independent of what the total mass of the atmosphere is. If the atmosphere were as dense as lead and 5,000,000 miles thick the gravitational force of something on the surface of the earth would be the same as if there were no atmosphere at all. The reason is that for a spherically symmetric mass distribution^*, the gravitational force is determined only by how mass there is inside of where you are. One way to convince yourself that this is true is that if you are at the center of the earth you would experience no weight because there is just as much mass no matter which direction you look. Here is one technicality: because the atmosphere is not dense we normally ignore the buoyant force (although you certainly can't for a blimp, for example). However, there is a tiny buoyant force which makes our weight appear to be less (your weight is still the same, there is just a different force up); hence, your friend is wrong on two counts since if the atmosphere were less dense as it is on Mars, there would be a smaller buoyant force so objects would appear to weigh more.

^*This means that the density depends only on how far you are from the center, not on where you are angle-wise; so everything looks the same at the north pole as at the south pole, for example.

QUESTION:
I would like to know what impact did Millikan's oil drop experiment have on science during and before 1920? Why is the electron charge so important? What is used for?

ANSWER:
This is a strange question! I believe that understanding the world around us in as much detail as we can is required by the human spirit. If you did not know the electron charge you could have no atomic physics. Experiments like that done by J. J. Thompson were able to measure the ratio of the charge to the mass, but to get either you had to measure one independently which is what Millikan's experient did. So you could say that knowing the charge gives you the mass and knowing the mass of something is important in physics. The electron charge is used, like many other fundamental constants, for understanding the universe; what could be more important than that?

QUESTION:
Where does the word "moment" in "moment arm" come from? How do the two terms relate to one another in analyzing torque?

ANSWER:
An alternative word for torque is moment, so moment arm is the distance from the axis around which torques (moments) are calculated. The torque is generally written as the moment arm times the component of the force perpendicular to the moment arm. A completely equivalent writing of torque is force times the component of the moment arm perpendicular to the force; I call the component of the moment arm perpendicular to the force the effective moment arm.

QUESTION:
I am an 8th grade teacher trying to teach Physics. When I make up word problems for force, am I always using acceleration due to gravity. For example: I can say a 15 kg object is being accelerated 9.8m/s², what is its force? But can I say a 20 kg object is moved 2m/s² what is its force? Are not all force problems using gravity as acceleration?

ANSWER:
The basic law is Newton's second law, F=ma which relates the net force F experienced by a particle of mass m which has an acceleration a. When a 15 kg object is freely falling the only force on it is its own weight (assuming no air resistance), so if we measure its acceleration to be 9.8 m/s² the weight must be 15x9.8 kg m/s²=147 N (newtons)=33 lb. For the object of mass 20 kg which is measured to have an acceleration of 2 m/s², the net force on it must be 40 N which is about 9 lb; since its weight is 20x9.8=196 N, there must be other forces on this object. An object may certainly have an acceleration different from 9.8 m/s². For example, a box sliding across the floor might have an acceleration of magnitude 2 m/s², that is as each second ticks by the speed gets smaller by 2 m/s so if it starts with a speed of 10 m/s it takes 5 s to stop. (We usually say that the accerleration is, in such a case, negative, but the important thing for 8th graders to understand, I think, is that acceleration tells you how the speed changes, so you should think of an acceleration of 9.8 m/s² as 9.8 (m/s)/s so that if you drop something it has a speed of 9.8 m/s one second later, 19.6 m/s two seconds laterr, etc.) If you are in the US, it would probably be helpful for your students to know that 1 N=0.225 lb since they probably think in terms of pounds; so a newton is about a quarter of a pound.

QUESTION:
I'm interested in understanding the interactions between subatomic particles. So I would like to ask two questions. 1. Is there any thinking or explanation of how the charges between the electron and proton are so evenly balanced, despite the large difference in their respective masses? It seems like there would logically be some underlying similarities that I don't see discussed very much. 2. If these parcicles are really "smeared" like a probability function, how can they exist for so long?

ANSWER:
Why would the relative masses have any correlation with the relative electric charges? If electrons and protons were not of identical charge, the universe would be a very different place since atoms would not be electrically neutral. Since the electric force is very strong, the lack of neutrality of matter would cause there to be no objects as we know them (the repulsive electric force would tend to keep objects from coalescing. And, what does a particle being smeared have to do with its existence?

QUESTION:
If two cars approach each other from opposite directions, each traveling at a speed of 50 km/h, each car one would perceive the other as approaching at a combined speed of 50 + 50 = 100 km/h to a very high degree of accuracy. But two spaceships approaching each other, each traveling at 90% the speed of light relative to an outside observer, do not perceive each other as approaching at 90% + 90% = 180% the speed of light; instead they each perceive the other as approaching at slightly less than 99.5% the speed of light. Why does this happen?

ANSWER:
Of course I cannot give you a complete explanation since that would require that I do a complete exposition of the theory of special relativity. Relativity is the reason. Relativity is based on the postulate that all observers, regardless or their motion or the motion of a source of light, will measure exactly the same speed for light in a vacuum. So, if you measure the speed of some particular beam of light to be c, somebody moving with the speed of 95% the speed of light relative to you will measure the speed of the beam to be c also. One of the consequences of this postulate is that no object can move faster than the speed of light relative to any other object. Hence, having two objects have a relative speed of 180% violates this rule. The speed of light is a universal speed limit. If you are truly interested, you should learn the theory of special relativity; it requires only algebra to understand it.

QUESTION:
I have a major question in my mind and I have not found any website that helps me and so please help me to answer my question: How is time affected by the amount of mass? For example: if we put a cart on a slope which is 10.3 g, the result will be 3 seconds... In addition, if we change the mass into 15 g, there will be an increase of time which will be 7 seconds... ( I have conducted an experiment exactly like the example above, and I see that the more mass we put on the cart, the longer time we will get)

ANSWER:
Simple physics would say that there should be no difference if there were no friction. Also, if there were friction and it was proportional to the weight, the times would be the same. However, if the friction were not proportional to the weight, for example the lighter car had a frictional force 1/10 the weight and the heavier car had a frictional force 2/10 the weight of the car, the heavier car would have a smaller acceleration as you have found. See earlier answer on this subject.

QUESTION:
My 8 year old son would like to know if an object is moving faster than the speed of light, will it cast a shadow.

ANSWER:
The groundrules of this site clearly state that I no longer answer questions about going faster than the speed of light. However, I want to encourage inquiring young minds, so I will make an exception. No object may go faster than the speed of light or even as fast as light. The reason is that the theory of special relativity, which is extraordinarily well-verified experimentally, shows that the energy required to accelerate an object to the speed of light is infinite and, of course, there is not an inifinte amount of energy in the universe.

QUESTION:
if you have a car in the air and you fill the tires to 35 psi, when you put the car on the ground the psi stays at 35 with the weight of the vehicle on the tires. why?

ANSWER:
I have previously answered this question.

QUESTION:
How far would a golf ball travel on the moon if hit at a 45 degree angle at 200 km/hour?

ANSWER:
I first checked and found that the speed you indicate is far less than the escape velocity on the moon. I then assume that the height attained and the distance traveled will be small compared to the size of the moon so that I can assume that the moon is flat, just as we do when we do such calculations on earth. The acceleration due to gravity on the moon is about 1.6 m/s (compared to 9.8 on the earth). Then I find (I presume you just want an answer, not all the details) the ball will be in the air for about 49 s, travel a distance of about 1930 m, and achieve a height of about 483 m. Since these are very small compared to the radius of the moon, my assumptions are fine.

QUESTION:
Does noise require energy to happen?

ANSWER:
I presume you mean sound noise. Sound is a wave and sound waves carry energy. Therefore, the source of the noise must supply energy.

QUESTION:
Somewhat technical question, so I don't know if it breaks the ground rules. I work in MRI and have had some QM courses a long, long time ago. But this continues to puzzle me. I don't mind at all looking it up in the QM books if only I knew what to look under. Could you provide a reference or the correct "topic" I could read up on? A charged spin-1/2 particle has a gyromagnetic ratio. For example, a proton has a QM spin-magnetic moment. When it is placed in a constant and uniform magnetic field its magentic moment will be at an angle (about 54.7 degrees) to the direction of the applied uniform magentic field and it will precess around the direction of this applied, external field. The proton will radiate as it precesses in the magnetic field. This can be detected by pickup coils. For example, this is how an MRI system works. (But I am interested in a single particle case, not in an ensemble of particles.) Question: Where does the energy come from to drive the precession and the associated radiating process as the particle precesses? If from the magnetic field, then wouldn't this "drain", say, a permanent magnet (system of magnets) generateing the magnetic field? That doesn't seem right (but maybe).... Being in a uniform magentic field, the gradient of B would be zero. So I guess there wouldn't be any net translational force on the particle. I think this is because there would not be any difference in energy between being at p1=(x, y, z) and being at p2=(x+dx, y+dy, z+dz) so no net force to translate the particle from p1 to p2. So does the particle just sit there radiating as it precesses? That doesn't seem right. If it radiates it should be loosing energy and going into a lower energy state. But there doesn't seem to be a lower energy state to go into? Or, for every "bit" of energy radiated it must be getting that amount of energy from someplace else, but where/how? That is what is confussing to me. If the magnetic field were not uniform I could see that the particle would translate into a lower energy state and would convert some of the potential energy into kinetic energy and radiation energy. But in a constant uniform magnetic field?

ANSWER: {this answer is not complete yet, I have to go to a concert!}
Your question is closer to breaking groundrules for not being concise and well-focused than being too technical. However, I will answer it because it is interesting. If you work with MRI, I am afraid I must tell you that you do not really understand what is going on. If a classical magnetic moment is placed in a uniform magnetic field it will align with the field. That is what it wants to do. If it is a quantum mechanical particle (that is it has a spin angular momentum) it cannot align with the field because the component of the total angular momentum (which is J=ħ√[3/4]) along the field direction may be only ±½ħ. That is where your angle comes from, cos(54.7)=½/√[3/4]. It is not really correct to say that the proton precesses; it is more correct to say that it is equally probable to be at any azimuthal angle and so many texts describe this situation as precession. Go ahead and think of it as precession, but it certainly does not radiate energy. Note that the moment is "up", that is 54.7⁰ relative to the field direction. Its other state, 54.7⁰ relative to the opposite direction ("down") is at a higher energy because it takes work to take the "up" aligned moment and turn it to a "down" moment. Let us say that it takes an energy E (which depends on the field strength) to flip the moment from up to down. In an MRI what happens now is that we shine in some electromagnetic radiation. If the radiation is of just the right frequency, that is f=E/h, there will be a high likelihood that the radiation will be absorbed resonantly (hence the "R" in MRI, magnetic resonance imaging). This absorption is what is detected in MRI. This is a very simplified overview, but it gives the basic physics principles. The details of how the whole imaging process is very much more complicated because of the problem of locating where the absorption is taking place.

QUESTION:
I was wondering if it is possible you could explain to me the basic facts of how zero point energy works. If you could explain in most basic form please as I am not very physics or maths orientated. I have heard it could be used as a prepulsion method. However I cannot find anywhere an explanation i can really understand.

ANSWER:
The only meaning zero-point energy has to me is the lowest possible total energy of a quantum mechanical system. Take, for example, a mass hanging on a spring; classically the lowest total energy of this system is zero corresponding to when the system is at rest. However, a simple harmonic oscillator (which is what a mass on a spring is called) is a classic problem in quantum mechanics because it is a system which can be solved analytically. It turns out that it is impossible for the mass to be exactly at rest, it must have some very small motion and the energy of the system in its lowest energy state is called the zero-point energy. The reason you are not aware of it in everyday life is that the motion is so incredibly small for a macroscopic size mass on a spring that you could never hope to observe it. On a microscopic scale, however, it is observable. For example a diatomic molecule may be modeled as two masses connected by a tiny spring and the lowest state is not with the molecule at rest. Obviously, this is nothing which you could use for propulsion.

QUESTION:
if an object is falling at a fixed rate of 500 feet per minute, what g-force will that object experience upon impact on the earth's surface. If possible include the formula so other rates could be used, since I would also like to calculate the g-force for the forward motion at different velocities. FYI: this is an attempt at calculating the best combination of conditions for an off-airport landing in un-inviting terrain by an aircraft experiencing complete power loss.

QUESTION:
I fell down the stairs two years ago and am still wondering what effect the impact might have had on my brain. I fell head-first from the top to the bottom, and hit the wall where it meets the small landing at the bottom - with my head. My body kind of crumpled to my left. I fell 11 steps of normal height, with my body turning head first, without touching the wall or railing. The landing at the bottom is about 3 feet from the stairs to a plaster wall. The impact was at the top of my head. Please let me know the fall's velocity and force of impact of my head - and if you can, how my brain would have moved inside my skull after the impact.

ANSWER:
Both of these questions are unanswerable because the force is proportional to the acceleration, that is the time rate of change of velocity. So knowing the velocity when an object hits and the fact that it is at rest afterward gives you the change in velocity but you cannot compute the rate of change of velocity without a time. So, if an object changes its speed by 500 ft/min =2.54 m/s, its mass is 100 kg, and it stops in 0.5 s, the average acceleration is 2.54/0.5=5.08 m/s² and the average force experienced is ma=100x5.08=508 N=114 lb. Since the weight of 100 kg is about 220 lb, the force of the ground must be 114+220=334 lb. So the force you would feel is larger than your weight by 334/220=1.5, so you would feel a 1.5 g-force. This is an example, but if either of these questioners really wants an answer, more data are needed.

QUESTION:
While working out I was lifting dumbbells and had the following question...what percent of the work is gravity doing when I curl a 20kg dumbbell? For a specific example, here are some numbers that may help…say I have a 20kg dumbbell and I’m doing curls with one hand. It takes me 5 seconds to raise the dumbbell and 5 seconds to lower it. My arm is about 35 cm from the elbow to the hand and my elbow remains stationary during the curl. When I lower the dumbbell it is much easier, so gravity must be doing some of the work, right? So what percentage of the work is gravity doing while LOWERING the dumbbell in relation to the amount of work it takes me to RAISE the dumbbell? For example, if it takes me 10 Joules of work to curl the dumbbell and it takes me 5 Joules lower the dumbbell, then is gravity doing 50% of the work when I lower the dumbbell?

ANSWER:
Assume that the dumbbell is at rest at the bottom, then the top, then the bottom. The work that gravity does on the way up is 20x9.8x(-0.35)=-68.6 J; work is negative because the weight (20x9.8 N) is a force down and the vertical distance (0.35 m) is up. The total work done is zero and so the work you do must be 68.6 J. On the way down it is just the opposite, you doing negative work and the weight doing positive work. The total work that you do is zero as is the work done by gravity. Does this mean you have gotten nothing from the exercise? Of course not. It is just that asking what the work done on the dumbbell is is the wrong question. You should ask a more biological question like how much energy is required by your body to do this exercise. If you lift it very quickly you will still do the same amount of work on the dumbbell, but it will require less energy expenditure from your body than lifting it slowly.

QUESTION:
What would happen to an object if it suddenly became immune to gravit (silly thoiught that idea is)? Oddly it would depend what time of day it is. Assuming it's midnight when this immunitry strikes (ie it is on the outside of the earth's orbit) it would continue on a tangent to the orbit of the earth while the earth continues around the sun. I have worked out that the Earth veers away from that tangential line by over 4,000 km an hour. Is this right? If so the gravity iummune object would leave the earth's surface with a huge acceleration. (If it was midday when immunitry struck the object would suddenly appear to weigh a vast amount more). I realise that gravity is simple the result of objects following curved space, is not really a 'force' and so cannot have a anti-force (other than curving space the other way?!) and that all anti-gravuty devices are simply using magnetic or electrostatic forces. But this question has bugged me since reading a book calles The Seach for Zero Point.

ANSWER:
Here is the problem with trying to answer your question: for an object to be "immune" to gravity, it would have to have zero gravitational mass. But for it to behave as you expect, moving in a straight line with the constant speed it had at the instant of its immunity, it must obey Newton's first law which applies only to objects which have inertial mass. However, inertial and gravitational mass are the same thing (a long-held experimental fact and a cornerstone of general relativity theory). So, I am afraid that your question would fall into the same category as questions like "suppose we could go faster than the speed of light"; it is "suppose an object had inertial but not gravitational mass", an unphysical situation.

QUESTION:
Is there a way of determining how temperature affects diffusion. For example, say I have a jar filled with a foul odor and want to lower the temperature to the point that none of the odor diffuses through the molecular pores in the jar. Is there an equation or method for determining what the required temperature would need to be?

ANSWER:
This is a quite technical question. In order to calculate diffusion rate you must know the diffusion constant. The temperature dependence of the diffusion constant is given in Wikepedia and is an exponential function. You can then put this result into the diffusion equation and solve. As you can see, this is a complicated problem.

QUESTION:
I understand Bohr's idea about quantum amounts of energy and that a photon is emitted (or absorbed) when a electron changes energy states. And I have read several times that this idea explained the spectral lines of a hydorgen atom. But what I have not been able to find (and has caused me to bother you with this question) is how this expains the exact wavelength produced. Related, can you direct me to something that explains how the speed and/or frequency of an electron that is emitting electromagnetic wave relates to the wavelength of the light produced. Math equation on this last one is fine... I am sure the info is "out there" and/or in one of my texts, but I can't find it. Hints or help would be appreciated.

ANSWER:
The key is to understand the relationship between the energy (E) of a photon and its frequency (f). The photon is the quantum of light emitted when a transition occurs. This is the famous relationship Einstein discovered in his theory of the photo electric effect, E=hf where h is Planck's constant, h=6.62×10^-34 m²kg/s. Hence, if an atom makes a transition from a state with energy E₁to a state with energy E₂, the frequency of the emitted radiation is f=(E₁-E₂)/h. Then the wavelength (l) is just l=c/f where c is the speed of light.

There is no well-defined energy of the electron while it is emitting the photon, so your second question has no answer. Anyhow, it is probably not a good idea to take the idea of an electron crusing around in a well-defined orbit too seriously.

QUESTION:
In the Movie "The Core" They travel to the center of the Earth. Now if you were down there wouldnt gravity not effect you as much, or what because almost half of the earth is above you?

ANSWER:
The gravitational force is only caused by mass not outside you. Therefore if you go down to half the radius of the earth your weight will only be ⅛ of what it is at the surface. If you get to the center your weight will be zero. You might be interested in an answer to an earlier question.

QUESTION:
If you started with a lightbulb. Surrounded the lightbulb with a perfect glass sphere, which was coated on the inside, with a first-surface reflective mirror. Removed the air from inside creating a vacuum within... and turned the light on, then off... In theory, would the light inside the sphere bounce around within the sphere indefinitely?

ANSWER:
I have previously answered this question.
PS there is no such thing as a perfect vacuum either.

QUESTION:
Okay, let's say that the wind is blowing at a constant velocity of 30 km/hr from the south. If a person were travelling at the same constant velocity, would that person feel wind? Since the air around the person is moving exactly as fast as the person is, would it be safe to say it would be the equivalent of someone standing still when there is no wind outside?

ANSWER:
You are correct, you would be at rest relative to the air and therefore would feel no wind. An example of this is a hot air balloon or a helium filled balloon. One of the problems with using such vehicles to move around is that they can't be steered, they are totally at the mercy of the winds and go where they are blown. An airplane can only steer because of the air moving past its surfaces.

QUESTION:
If there were a civilization on a planet orbiting Alpha Centauri 4.37 light years away, how big would the diameter of their radio telescope have to be to clearly receive a TV signal from Earth? I asked the people at SETI the same question once and never got an answer.

ANSWER:
OK, I will take a stab at this. But, I am not an engineer and do not really know for sure how much information one must receive to be able to put together a tv picture. I will assume that, since the wave nature of the radio waves carries the information, we will need at least one million photons per cycle of the wave. My thinking is more in line with AM radio waves where there is one constant frequency of carrier waves and the information is carried by the amplitude of the wave; I realize that this is not really what tv is but it should give an order of magnitude estimate. The typical power of a tv station is about 100 kW=10⁵ J/s. The energy of a single photon is hf=6.6x10^-34x10⁸=6.6x10^-26 J/photon so for our power source we have N=10⁵/6.6x10^-26=1.5x10³⁰ photons per second. The frequency of a tv station is about 100 MHz= 10⁸ s^-1. To get 10⁶ photons per cycle we therefore need 10⁶x10⁸=10¹⁴ photons per second. 4.7 ly=4.4x10¹⁶ m so the intensity (in photons/second/square meter) at Alpha Centauri will be about 1.5x10³⁰/[4p(4.4x10¹⁶)²]=6x10^-5photons/s/m². We therefore need an area of 10¹⁴/6x10^-5=1.7x10¹⁸ m². That is about an 800,000 mile square. This hinges mainly on my assumption of needing 10⁶ photons per cycle of the wave which might be wrong by several orders of magnitude.

QUESTION:
Can beef melt? This will help me settle a long-standing debate with a coworker.

ANSWER:
There is no definitive answer to this question because beef is not a homogenous substance like iron or water or salt or oxygen or whatever. It is a mélange of many different things. It has lots of water in it and we wouldn't argue that water can melt; thaw a frozen steak and the ice in the steak melts and becomes water. It has fat and we wouldn't argue that fat melts; put it on a fire and watch the melted fat drip onto the coals. But it also has lots of organic molecules which, when heated, change their molecular identity, that is heat causes a chemical change rather than a phase change (which is what melting or evaporating are). When you cook something, that is what you do—cause the food to undergo a change into something different from the uncooked food. So regardless of which side of this argument you are on, you both win and lose!

QUESTION:
an arrow is shot up from the ground at 30 m/s one second later, another arrow is shot up from the ground at 40m/s what is their displacement from the ground when they collide? (This was the most difficult question on a test that i had 2 days ago. The top 5 students of the class all got different answers. My answer was around 170, i don't remember exactly, i just want to know the answer.)

ANSWER:
I only need the kinematic equations y=y₀+v₀t-½gt² and v=v₀-gt and I use g≈10 m/s² for calculational ease. First, find out where the first arrow is and how fast it is going after 1 s. y(1)=30x1-5x1²=25 m and v(1)=30-10x1=20 m/s; the purpose of this step is to find the initial conditions for arrow #1 to use in the next step of the problem. Now write the y equations, choosing t=0 when the second arrow is shot, for each arrow. y₂=40t-5t² and y₁=25+20t-5t² (we don't need the v equations since we are not asked for any speeds). Now set y₁=y₂ and solve for t and find t=1.25 s. Put this t into either y equation and find y=42.2 m. You could go on and write the v equations to find out the velocity of each when they collide. v₁(1.25)=20-10x1.25=7.5 m/s and v₂=40-10x1.25=27.5 m/s.

QUESTION:
Take a look at this website: http://web.jjay.cuny.edu/~acarpi/NSC/3-atoms.htm It's from CUNY so they are not exactly cranks. Note in the 3d paragraph they say centrifugal force keeps the electron from coming into contact with the nucleus. Is the CUNY website wrong?

ANSWER:
This is atrociously poorly written! Believe me, centrifugal force is not a real force. In even the most elementary physics course we learn that a force perpendicular to the velocity (as in an orbiting particle) causes the direction, not the speed, to change. Hence there is no reason to ask the ridiculous question of what "keeps the two particles from coming into contact with each other" since the orbiting particle just orbits. Let me try to clarify what centrifugal force is. As I have alluded to above, we easily calculate a circular orbit for a particular force and velocity using Newton's second law, F=ma, where F is the electrostatic attraction to the nucleus, m is the electron mass, and a is the acceleration where a=v²/r for circular motion and r is the orbit radius. Now, suppose that you are standing on the electron; how do you describe the situation? Well, Newton's laws are not true in an accelerating system which is the case here. And it is really obvious that they are not valid because there is only one force and yet, if you are in the electron's frame of reference, no acceleration. But suppose that you insist on using Newton's laws to describe your motion; the only way you can do that is to invent fictious forces to make things work out. In the case we are discussing the electron is not accelerating and there is one real force pointing toward the nucleus of some magnitude F (this is referred to as the centripetal force, center seeking if you know your Latin); but the sum of all forces must be zero and so you must postulate the existence of a force which has magnitude F and points away from the nucleus (centrifugal force, center fleeing if you know your Latin). That is not really there but it is often very much to our advantage to force Newton's laws to be true in accelerating (so called noninertial frames of reference) for computational reasons. Let me give you a couple of other examples of fictious forces.

Suppose you slam your foot on the accelerator of your car. You feel a force pushing you back in your seat, right? There is no such force; the only force on you is the seat back pushing you forward and since you would like to use Newton's first law your brain perceives there to be a force pushing you back.
What force makes weather patterns circulate? Because we are on a rotating earth there is a fictious force called the coriolis force. Long-range artillery gunners have to correct for this "force".

I can't imagine what course the CUNY page was supposed to serve, but probably a physics for artists kind of course where the students were assumed to be incapable of understanding Newton's laws or what acceleration is. My own feeling is that anybody can understand these if motivated.

QUESTION:
What is the correct equation for momentum in Newtonian physics? I thought it was mass X acceleration. (And I've never understood why it would be mass X acceleration.) It seems to me it should be mass X velocity. When I looked up momentum on Wikipedia, it gave the equation: mass X velocity. (Which makes sense to me.) But I could swear when I was in college the equation for momentum was mass X acceleration. On the other hand, I didn't do so well in college physics, so maybe I'm remembering it wrong.

ANSWER:
You are right, it is p=mv. The reason that ma sticks in your head is that Newton's second law may be written F=ma. There is another connection: since a is the time rate of change of v, dv/dt (do you know calculus?), Newton's second law may be written F=dp/dt, that is, force is the time rate of change of momentum. This is how Newton originally expressed it and is the way you must express it in special relativity, that is F=ma is not true in special relativity. In special relativity, though, momentum must be redefined to be p=mv/√(1-(v²/c²)) where c is the speed of light. Note that when v<<c, p≈mv.

QUESTION:
I don't know very much about how light works. And for some reason this idea just came to me. if there was a video camera that took the video with an extremly high frame-rate would some of the frames be blacked out, or would there be some picture missing from it because there wasn't any light in it at the time? So is it possible that light could travel in waves of particles, much like this: ))))) So everything we see is actually like a series of pictures with a rediculesly high frame-rate? ( . the dots are pictures the video camera takes and, ) brackets waves of light particles and the image that comes with it) could the camera take pictures between the waves. like this: ).).).).)?

ANSWER:
Light may be thought of either as a wave or as a stream of particles (called photons). However, it would not be possible to take light which you would otherwise send into a camera and make a shutter speed high enough to let through zero photons; there are simply too high a density of photons in a visible beam of light. However, if you had a very low intensity light ray, you could arrange it so sometimes the shutter would let through only one photon, sometimes none. So each frame would have zero or one little dots on it. If you ran the movie you made at say two frames per second you would see individual flashes as the photons hit the film; if you ran it at real time the frames would be too close together for you to perceive anything but the totality of all the photons, the image of the original object.

QUESTION:
A friend of mine who is an electrical engineer told me that a prof once told him electrons don't actually orbit the nucleus of the atom. Is this true? My friend says there is experimental evidence that sometimes the electron goes right through the nucleus. We were drinking beer when he told me this, so is this just BS or is there some truth to it? Lastly, assuming electrons really do orbit the electron, I believe they move very fast. Do they move fast enough to gain mass due to relativity? Also I assume the weak nuclear force has to be pretty strong to keep the electrons from flying away due to centrifugal force. On the other hand, even a weak battery can make electrons flow in an electrical current. So how can the electrons withstand centrifugal force as they orbit the nucleus and yet move so easily in the flow of electricity?

ANSWER:
Part of your question has been answered earlier. It is a useful but inaccurate picture to imagine electrons in little planetary orbits around the nucleus. When scales get as small as atomic distances the identity of a particle becomes inaccurate and we should think of particles as being represented by probablility distributions, that is a mathematical distribution that allows you to predict the probability of finding the "particle" in some particular small volume. Therefore it is more accurate to visualize an electron as being a cloud in the atom, the cloud being more dense where the particle is more likely to be. This probability distribution extends right into the nucleus and therefore there is a nonzero (but still very small) probability of finding the electron inside the nucleus so, indeed, the electrons do sometimes pass through the nucleus.

Electrons move very fast, but relativity is only a minor correction. Anyway, I have argued that you shouldn't think of mass increasing with speed.

The final question is completely different from the others. A solid is bound together by the clouds of adjacent atoms interacting and forming bonds. In some materials, which we call conductors like copper, silver, etc., the outer electrons become essentially free to move around in the material; in fact these electrons behave pretty much like a gas inside the solid. When a "weak" battery is connected across such a material, it is like a fan in a gas and it causes the electrons to drift in the direction from negative to positive.

QUESTION:
How do you go from the fully relativistic form for Kinetic Energy, to the more well known ke=1/2mv²?

ANSWER:
This is a standard derivation which can be found in nearly any textbook which covers special relativity. The trick is to do a binomial expansion of the square root:

KE=m₀c²[(1-b²)^-1/2-1]≈m₀c²[1-(-½)b²+…-1]≈½m₀v²where b=v/c and c is the speed of light. I have used (1+x)ⁿ≈1+nx+… for small x.

I hope this was not a homework problem since I don't like that and you would have cheated!

QUESTION:
Is there any relationship between a sine wave and the bell shaped curve used in statistics? They look similar. Is there a reason for this or is it just a coincidence? I suppose a mathematician could come up with a formula to describe the relationship. However, would such a formula have any significance? (It just occurred to me I'm asking the same question twice. If such a formula lacks significance that implies any relationship between the two curves is just coincidence.)

ANSWER:
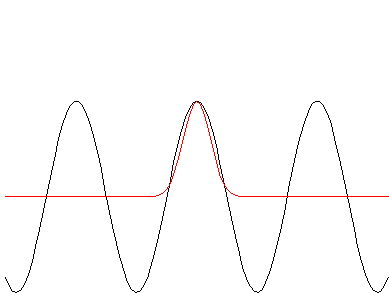
You have been looking over too restricted range if you think that a bell-shaped curve and a sinesoidal function have similar shapes. To the left is a comparison between the two. Once you get away from the central maximum of the bell-shaped curve there is no relationship between the two. There is no mathematical relationship between the two functions however you could make a bell-shaped curve by adding an infinite number of sinesoidal curves with appropriate weights; this is called a fourier transform representation of a gaussian function (another name for a bell-shaped curve).

QUESTION:
There is a lot of "missing mass" in the Universe. Galaxies furthest away from us are receeding at close to light speed (~c) -- and we are receeding from them (relatively) at ~c. When objects move at close to c their mass increases. Could galaxies receeding from each other (relatively) at ~c be gaining extra mass that accounts for the "missing mass" in the Universe?

ANSWER:
First, I always have told students to not take too seriously the often stated claim that mass increases with velocity; see the answer to an earlier question to see my viewpoint on mass. I had a long discussion with a friend who is an astronomer quite well versed in the theory of general relativity. He argues that this could not possibly explain dark matter for a number of rather esoteric and complex reasons which are beyond the scope of this site. However, there is one simple example which should put the matter to rest: in our own galaxy where no objects have speeds anywhere near approaching the speed of light relative to earth, there is a severe dark matter problem. The orbital velocities of stars around the center of our galaxy cannot be understood in terms of observable mass in the galaxy; the similar motions of other galaxies as well as our own are the best evidence that we do not understand something about celestial mechanics and the postulation of a mysterious dark matter is one hypothesis to explain these problems.

QUESTION:
is there pure concussive effect of an explosion in a vacuum

ANSWER:
I am not sure what you are asking. However, concussive means the ability to shake or agitate and in the case of an explosion would mean the propogation of a pressure pulse and, of course, that cannot happen in a vacuum. When you see a space movie and there is the explosion of a Klingon starship, you would not really be able to hear it even though all space movie directors seem to think you could.

QUESTION:
Would it be possible, with respect to efficiency, to build a minature electrical generator to attach to an axle of a car, transfer the electrical energy generated by the rotating of the axle to a rechargeable battery? This would be done in order to transfer the stored energy to your home when your car is parked in your garage. If you had a system set up where you had a plug that you could connect from your rechargeable batteries in the car to the input of electricty to your house? This question has been on my mind since I read about using wind and or hydroelectic power to cut down on your energy bills.

ANSWER:
This is essentially how the electrical system of your car already works, that is your alternator recharges your battery so you can always start up your car (or listen to the radio when the car is not running). If you put a generator on your car you can't turn it for free, that is you must supply the energy which you are storing in batteries and so your gas mileage will plummet. Furthermore, if you are going to carry enough batteries to make a serious dent in your household needs, the large weight of these will also cut down your mileage. Since electricity is relatively cheap and gasoline is relatively expensive, this idea is not a viable one. You may be interested in an alternative which is one of the ways hybrid cars work: if you connect your generator to your wheel only when you want to brake, then the kinetic energy of your car will be converted into electrical energy instead of into heat which is what conventional brakes do. This energy from braking is used to charge up the batteries used to run the car in its electric mode.

QUESTION:
i really need help with prooving/finding something. I have no idea how to do it and everyone i ask has the same problem, but i think it can even be done without calculus. The question goes as follows: If i have a box on a surface with coefficient of friction= mu (not given) and i pull the box with a force T at theta degrees above horizontal, find as a function, at which angle will i MAXimise the acceleration for any value of mu? (as a function?). So naturally my first step was to realized what they wanted and i got: T(cos[theta]) - ({mu}[mg - Tsin{theta}]) = ma (where m= mass, a = acceleration etc..) Now i have tryed rearanging it, finding inequalities and many more things but i just cant find it!! I really dont know how to do it and i would be so happy if you could show me!

ANSWER:
I don't know how to solve this without calculus, but it could probably be done if you were clever. Your equation is correct, Tcosq -mmg+mTsinq=ma. If you solve for a and then differentiate a with respect to q and set the result equal to zero you will find: tanq=m.

QUESTION:
I have learned that we all will inhale (at least once in our lives) the very same atoms as our ancestors from thousands of years ago. If this is true, does this mean that our bodies atoms are bound to this Earth and remain here permanently after we die. Does our atmosphere and (or) gravity restrict our atoms (after death) to the Earth, or can our atoms find their way off the Earth into space and possibly to other worlds? I ask these questions for spiritual reasons and out of true scientific curiosity.

ANSWER:
Suppose that we assume that the atmosphere gets completely mixed up by weather patterns after a relatively short time, say a year; this essentially means that a molecule here today is equally likely to be anywhere else in the world in a year. Now, I calculated the volume of the atmosphere assuming it to be 20 km thick; that would include most of the molecules. Now, I assumed a typical human breath is about 1 liter; then I find that the number of lungs full of air there are in the atmosphere is roughly 1.5x10²¹. Next I roughly estimate the number molecules in one lung full of air to be about 3x10²². So, if I take one breath and redistribute the air over the whole atmosphere, I will find about 20 molecules of that air in any other breath. So, very roughly speaking, each breath you take will have 20 molecules of the last breath John Kennedy took before he died. But, we might more likely be interested in the number of molecules over a lifetime; taking Leonardo da Vinci, who lived to age 67 as an example, the number of breaths breathed in his lifetime was about 7x10⁸(I assumed about 20 breaths/minute), so every breath you take will contain about 1.4x10¹⁰ molecules (that is about 14 billion) that were breathed by da Vinci! Keep in mind that my calculations are very rough but they should give a good approximation of orders of magnitude.

Your second question is not really related. Gravity does a good job of keeping most molecules in the atmosphere confined to this world. However, there are virtually no hydrogen molecules or helium atoms in the atmosphere because they have escaped into space. Helium is recovered as a byproduct of natural gas, having been confined underground where it cannot escape. The reason for this is that temperature is a measure of the average kinetic energy of the molecules and lighter molecules have much higher speeds than say oxygen or nitrogen at the same temperature. The speeds are large enough that the fastest have a velocity larger than the escape velocity and fly off into space. For the same reason, the moon has no atmosphere because the escape velocity is much lower and all the gas escapes.

QUESTION:
I've been wondering for a while about the effects of fusion on gravity. Fusion is a process by which lighter elements join to make heavier elements, releasing large amounts of energy at the expense of small amounts of matter. However, concentration of large amounts of matter defines gravity as a curvature of space. If matter is lost due to fusion, does the gravity which that matter represented go away too? Is it redistributed somehow?

ANSWER:
Let's imagine a universe with no mass, just photons. Then I believe that spacetime would be flat. So, when mass gets smaller spacetime gets less curved. Realize, however, that the fractional change of mass in a star over its lifetime never really approaches a large fraction. You should not think of gravity as being something which is conserved (as implied by your question "Is it redistributed somehow?"). If there is one mass there is a gravitational field; if it is made to go away (conserving energy), the gravity goes away too.

QUESTION:
I don't know if this is a silly question or not, but I can't find it in your old answers (at least, not in a form that I understand). There is a lot of "dark matter" in the Universe; and mass increases as matter moves nearer the speed of light; the galaxies are moving away from each other at the speed of light. Therefore, doesn't the mass of the galaxies increase enormously as they are moving away from each other? Couldn't this account for the missing mass of the "dark matter"?

ANSWER:
For starters, dark matter is hypothetical and has never been directly observed. The universe is expanding but the speed of the most distant objects is not the speed of light, in fact not really close to the speed of light even though they are moving rapidly, just not that rapidly.

"CORRECTED" ANSWER:
I talked with an astronomer friend and found out that in fact the most distant objects are moving with a speed quite close to the speed of light (about 95%). Nevertheless, this cannot be the answer to the dark matter puzzle for reasons explained in a similar answer above.

QUESTION:
A metal spoon and a wood spoon have been in boiling soup for a long while. If I take out both spoons, the metal one will feel hotter. Does the metal spoon in fact have a greater temperature or is it just a better conductor? I guess my real question is how can this guy be holding a white hot space shuttle tile in his bare hand that is 1260 degrees C? Can two objects have equal temperature where one burns you yet the other does not? http://upload.wikimedia.org/wikipedia/en/thumb/5/5b/TPScube.jpg/300px-TPScube.jpg

ANSWER:
It is because the metal is a better conductor. They both have the same temperature (assuming that they were both submerged). This is why you never see fire walkers walk on red-hot metal surfaces. The reason the man can hold the hot shuttle tile is because it has been heated up locally so that it is hot where it was heated up but not hot where he is touching it; this is because the tile is a very poor conductor of heat. In the spoon example maybe I misunderstood what you meant. If the two spoons are in the soup with their handles sticking out, the metal handle is hotter the metal is a better conductor.

QUESTION: ;
The reason for this email it’s because I have a question about the ocean tides here on earth. I understand that gravity bends time/space based on Albert Einstein’s theory. My question is: Do the ocean tides follow the path of the space bent due to the presence of the moon? I'm working on a presentation and I wanted to talk about this subject and at the same time give a graphical representation of this phenomenon. For some reason I keep thinking that this phenomenon can be explain showing the fabric of space being bent by the two bodies (Earth and Moon) resulting on the ocean tides in other words, the earth will look oval due to the ocean waters. The small deformation of space due to the moon's presence will create an oval looking basket on earth's space forcing the waters to fallow this shape depending on the moon's position. It’s this some what correct?

ANSWER:
Suppose the oceans were full of molasses; the tides would be much smaller, probably not perceptable at all. And yet, the curvature of spacetime would be the same. It is therefore fallacious to assume that the shape of the ocean reflects the shape of spacetime. Curvature of spacetime is best visualized by observing the bending of light by strong gravitational fields. Research this and "gravitational lensing" for your presentation.

QUESTION:
Who was most responsible for the Grand Unification Theory?

ANSWER:
There is no single GUT. Read the Wikepedia entry on GUTs.

QUESTION:
why does fire burn up? I mean if you point a match down the falme still goes up, why doesn't gravity draw the fire to the ground rather than the sky?

ANSWER:
I have previously answered this question.

QUESTION:
My question relates to how icebergs reflect the heat of the sun back out of the atmosphere. I know that white reflects light, but does it also reflect heat? This is mysterious to me. What about a mirror? If the sun shines on a mirror, does the mirror effectively redirect the light and the heat? If, in a dark room, I blow hot air onto a white block of ice, will it reflect away? Are the sun's light and heat one radiation or two?

ANSWER:
When we talk about heat we are talking about energy transfer and that can be accomplished in several ways thermodynamically. Heat energy from the sun is simply the infrared portion of the electromagnetic spectrum which is comprised of light with wavelengths somewhat larger than can be seen by the eye. When this heat hits a reflective surface it is reflected much the same a visible light. Blowing hot air, however, is a very different kind of heat transfer; this is basically forced convection where you move a volume of hot air to replace a nearby volume of cooler air. It is essentially meaningless to talk about reflection of this kind of heat transfer. There are other ways to transfer heat, the most important of which is conduction; for example, sticking an iron rod into a fire and waiting until your hand gets burnt.

QUESTION:
The situation is a ball attached to a string like a swing. Apparently, no work is done on the string, but surely the weight of the ball has a component that is in the same direction of the motion of the ball, so some work is done on the string.

ANSWER:
In the case of a simple pendulum the ball is considered to be a point mass and the string to be massless. If the string is massless you cannot do work on it because it can acquire neither kinetic nor potential energy. If, however, the string has mass, work will be done on it by the ball and by its own weight. In fact, if the string has mass you don't even need a ball at the end. This is called a physical pendulum, one consisting of things other than point masses and massless pieces.

QUESTION:
The strong nuclear force is said to have a very short range, owing to the short lifetime of its carrier particle (at least as I was taught in high school many years ago). This rang is said to determine the maximum size of an atomic nucleus, hence this is why Uranium is the heaviest naturally occuring element; any larger a nucleus and the electromagnetic force would start to take over and the nucleus would fall apart. My question is: the above make sense only if the strong force originates from the centre of the nucleus, but it has always been explained to me as though all nucleons (even the ones on the edge) can experience the strong force (the classic demonstration involves magnets coverred with velcro to show how the replusion is overcome if you get close enough). So where does the strong force really come from and why do the outer nucleons 'feel' it to a lesser degree?

ANSWER:
It is an oversimplification to say that nucleus becomes unstable because of the Coulomb force becoming dominant over the nuclear force. And, it is incorrect to simply say that in a large nucleus the outer nucleons are "out of range" of the nuclear force. The nuclear force is the force between individual nucleons and so each nucleon interacts only with its nearest neighbors due to the short range of the force. The nucleons on the surface see only neighbors inside the nucleus and so they are bound to the nucleus as a whole. Those on the inside see essentially no force since each sees just as many neighbors in one direction as the opposite direction and all forces approximately cancel out. In fact the simple model that the nucleus is an impenetrable sphere (particles move freely but cannot escape) does a remarkably good job describing nuclear structure as long as you include the nuclear spin-orbit force which I will not go into here.

QUESTION:
Does the acceleration due to gravity change between day and night? During the day, the sun would pull us toward it thus lowering the earth's pull. At night, it would add to the the earth's pull, increasing gravity. Is this reasonable?

ANSWER:
The answer is yes, but the effect is very small, probably not measurable. I calculate the acceleration due to gravity at the earth's orbit due to the sun to be about 6x10^-3 m/s². Assuming that g=9.8 m/s², the two values would be 9.806 and 9.794 at the equator, less than 0.1%. This is small compared to variations in g due to the nonsphericity of the earth, local mass variations, the rotational motion of the earth and other effects.

QUESTION:
I am reading Roger penrose's The Emperor's New Mind, and on page 301 he says that when two slits are open the intensity at the brightest part of the screen is 4 times what it was before, rather than twice, as common sense would predict. I took that to mean that photons which are subject to positive interference carry more energy than before they passed thru the slits.

ANSWER:
I have previously answered a similar question.

QUESTION:
Regarding radiolysis, I have read about it in textbooks, but I still have the following questions: If the body is 80% water, doesn't radiolysis happen alot in diagnositc radilogy? If yes, why is this not a big concern-or is it?

ANSWER:
Radiation can be used to dissociate water. However, the probabilities are very small. A number that I could find to give an example is that only about 20 molecules dissociate for every 100 electron volts of radiation energy deposited. The energy of a typical xray is like 1000 electron volts so if completely absorbed could result in 200 destroyed atoms. And, of course, most xrays are not absorbed. Even if a million of them were, 200,000,000 is a tiny number compared to the number of water molecules in a thimble full of water.

QUESTION:
I'm sorry to bother you but this is something that has been bothering me for a while and I'd really appreciate your help. In Feynman's book on QED he cites that the probability that an electron will couple with a photon squared is 1/137 (or aprox. .085). He goes on to say that the proton has a 'magnetic moment' of 2.79. Now I assume that these two things are the same, the probability of and electron/photon coupling and the 'magnetic moment', since electromagnetic force is carried by photons. Therefore I would expect the 'at rest charge' of one proton would be greater than that of one electron in proportion to their coupling amplitudes; because in Feynman diagrams it is said that the reason particles of like charge repel each other is because they exchange a photon and the photon momentum knocks them away from each other; like billard balls. However, when I watched an online lecture from MIT on electricity and magnetism, the professor stated that the force between two repulsive electrons and two repulsive protons was aproximately the same. This is my point of confusion. Why are they the same?

ANSWER:
You have several very different things jumbled up here.

First the 1/137 number is called the fine structure constant and is the number which is used to characterize the strength of the electromagnetic interaction. It is a particular combination of physical constants like electron charge, speed of light, Planck's constant, etc.; see the Wikepedia entry for fine structure constant to get the exact definition.
The magnetic moment of the proton has nothing to do with the fine structure constant. Most elementary particles look like tiny bar magnets and the magnetic moment is simply an experimental measurement of the strength of that magnet. It is dependent on the structure of that particle and reflects what the density of electric currents is. A simple (overly simple) model would be that a proton is a charged sphere which is rotating and the rotation of the charge comprises a current which gives rise to a magnetic field.
The third statement, I believe, simply states that the electric charge on a proton is of opposite sign but identical magnitude as the the charge on an electron and has nothing to do with the magnetic moments or magnetic forces.

QUESTION:
I don't understand Newton's Third Law. If it is true then surely, for example, it is impossible to move your hand through a table since the reaction will always equal the weight.

ANSWER:
Newton's third law (N3) says that if one object exerts a force on another, the other exerts an equal and opposite force on the one. Many students misunderstand this law as you demonstrate in your example. Instead of talking about a hand, let us assume there is a book on the table. Are there any forces on the book? Yes, there is its own weight straight down (let's call that force W) and maybe the table, which touches the book, also exerts a force on the book (let's call that force T). Since the book is not accelerating, the total force on it must be zero (that is Newton's first law, N1) and so T must be a force straight up which is of the same magnitude as W. These forces are equal and opposite because of N3, right? WRONG, WRONG, WRONG! These forces are equal and opposite because of N1 and they have absolutely nothing to do with N3. They cannot be a N3 pair because both are on the same body (book) and N3 addresses forces on different bodies. So, what is the N3 (reaction) force which pairs with the force T? Since T is the force the table exerts on the book, N3 tells us that the book exerts a force down on the table which has the same magnitude as T. And, what is the N3 (reaction) force which pairs with the force W? Since W is the force the earth exerts on the book, N3 tells us that the book exerts a force up on the earth which has the same magnitude as W. That's right, the book exerts a force on the whole earth. N3 can never cause something not to move because the relevant forces are on different objects.

QUESTION:
In a standard Newton's Rings experiment, we place a convex lens of large radius over an optocally plane glass plate. What will be the fringe pattern if the optically plane glass plate is replaced is replaced by a concave lens, such that its radius is larger than that of the convex lens?

ANSWER:
It will still be a bullseye pattern but the fringes will be farther apart because the air gap widens more slowly as you go out.

QUESTION:
Why does the refractive index of a material change with wavelangth?

ANSWER:
Basically it is because the permittivity (e)of a material depends on the frequency of the electric field it experiences. And the speed of light is proportional to 1/√e. The reason the permittivity depends on frequency is that the interaction of varying electric fields is mainly the interaction with electrons bound to atoms. A simple model is to imagine the electrons bound by tiny springs to atoms. This then becomes the driven damped oscillator model and the response depends on how close the frequency is to the natural frequency of the electron on the spring (resonance).

QUESTION:
When a detector is placed at one of the slits in the double slit experiment with light, is the wave function collapsed by the observation of people or by the presence of the detector? (i.e. if a detector was placed at one slit, but no one actually looked at the results would you still get a interference pattern?) Also I am not including the actual interference pattern in the results, only the information given by the detector, the information of course being which hole the particle went through,

ANSWER:
Any measuring device which determines which slit the photon passes through will destroy the pattern, it does not require a human to know.

QUESTION:
When the leaf has fallen a certain distance its speed becomes constant, why?

ANSWER:
It has to do with air friction. When an object passes through a fluid like air it experiences a retarding force. This is how you can feel the wind, for example. This force depends on the speed of the object; it is easy to convince yourself of this by putting your hand out the window of a car at low and high speeds—greater force at higher speeds. To a good approximation, the force is proportional to the square of the speed so something going 80 mi/hr will experience 16 times the force as something going 20 mi/hr (which is why you should not drive too fast if you want to conserve gasoline). A falling object is speeding up as it falls from rest because of its weight which is a force down; but the air resistance, which is a force up, gets bigger and bigger as it speeds up until the force is equal to the weight of the object. Now the object experiences zero net force so it stops accelerating. This speed is called the terminal velocity. You can read much more detail in an earlier answer if you like.

QUESTION:
2 bicyclists on identical bicycles roll down a hill (starting from a stop or identical starting speeds). One bicyclist is heavier than the other; will this person reach the bottom of the hill faster?

ANSWER:
It depends on the assumptions you make. I will outline the essential considerations:

If there is no friction then they should both get to the bottom at the same time. This is because the force down the hill on each is proportional to the weight which is proportional to the mass so the accelerations are the same (I am assuming you know Newton's second law).
But there is friction in the bearings of the bike, the rolling friction of the tires, friction of the roadway, etc., but these are also approximately proportional to the weight, so again there should be a tie.
Air friction is determined by geometry and speed, so it is not determined by weight. The greater the speed the greater the force of air friction (approximately proportional to the square of the speed), so eventually an object will have a force from air friction precisely equal to but opposite the force from gravity and it will stop accelerating; it has reached its "terminal velocity". An object moving under the influence of gravity and air friction experiences a greater. The terminal velocity for the heavier person is larger, so if air friction matters (and it does because pedaling into wind is much like going up a hill) the heavier person will win. You can see more detail about air friction in an earlier answer.

Friction can be a complicated thing, so it would be interesting for you to try things out experimentally.

QUESTION:
Coulombs constant 9 x10^9 can be found as 1 / (4 pi x permittivity of free space ). It is also found as c^2 x 10 ^-7, or 1 / permittivity x permeabilty x 10 ^-7), why is this?

ANSWER:
If you measure the force between two point charges separated by a distance r, this force is found to be proportional to product of the charges and inversely proportional to r². If you measure the charge in Coulombs and the distance in meters, then k=9x10⁹ Nm²/C² as you state. This is simply an experimentally measured number, that is the force between two charges each 1x10^-3 C and separated by 1 m would be 9000 N, a number you could measure to get k. Suppose that you have a number N and you want to define a new number M=2N; that is all permittivity is, a redefinition of k, e₀=1/(4pk). Your last question is most interesting. The permeability of free space is m₀=4px10^-7Ns²/C² and, like k, it is just a proportionality constant which tells you the magnetic force between two current carrying wires. Now, it turns out that when you do the mathematics you find that the equations of electricity and magnetism (called Maxwell's equations) predict waves which have a speed of c=[e₀m₀]^-1/2 and this speed just happens to be the speed of light in a vacuum. And so if you now do the simple algebra, you find that k=10^-7/[e₀m₀]=c²x10^-7.

QUESTION:
I have heard that if one inhabited a two-dimensional macrocosm and a three-dimensional sphere passed through this macrocosm, then one would see a point grow into a circle, before collapsing into a point and disappearing again. Now I apologise for asking you about such an unscientific conjecture, but could it be that the appearance and subsequent disappearance of particles and atoms and so forth which has been observed by physicists to be occurring constantly; could it be that these transient particles are, de facto, entities from a higher cosmos passing through this three-dimensional cosmos?

ANSWER:
You are referring to virtual particles as you indicated in a later message. How can a particle, with energy mc², simply appear from nothing? The answer is that you can violate energy conservation as long as you also obey the Heisenberg uncertainty principle, i.e. as long as the time during which you violate energy conservation is short enough. Quantitatively, The product ET (energy time time) must be on the order of about Planck's constant which is a very small number (on the order of 10⁼³⁴ in SI units). So, you may spontaneously create 1 Joule of energy as long as it does not exist longer than 10^-34 seconds. This picture has done remarkably well in understanding virtual particles. (Incidentally, you cannot have a virtual electron, for example, because that would violate conservation of electric charge; instead you must have a vitrual electron-positron pair.) Could they be understood as evidence of higher dimensions? Scientists are loathe to say anything is not possible, but more than simple conjecture would be needed to convince anybody—predictions of nature are required for acceptance of a hypothesis.

QUESTION:
If there was no wind present what force would a raindrop hit a piece of wood, (siting on the gound) at? At what point would the force generated by a raindrop be enough to cause damage to a piece of wood? What is the wood was covered in a tar-like substance?

ANSWER:
A large raindrop has a terminal velocity of about 20 mi/hr. Have you ever been hit by a large raindrop? It does not really hurt so the force must be pretty negligible. The force of a raindrop hitting wood will not damage it.

QUESTION:
I've been looking at various videos on Youtube about homompolar motors. In some videos a battery is used and in other there is not, but in both types of set-ups... What is it that causes the spinning action. I can some what understand the spinning when a battery is used. In a battery set-up there is a current in the wire that makes a magnetic field around the wire, or wires, and it is this magnetic field that conflicts with the current in the wire causing it to be pushed away. But in the videos that don't use a battery what is making the whole assembly spin? I is my understanding that magnetic flux fields are stagnant. So when a charge is applied to the "no battery" homopolar motor is there a current traveling along the flux lines causing it to spin? I've attached some links to clarify my question:
http://www.youtube.com/watch?v=2hHfkK4iGBQ
http://www.youtube.com/watch?v=hXbFfMBW97A&mode=related&search=

ANSWER:
In each of your examples things get started with two wires. These are attached to a battery which supplies the current and gets things spinnining. A good explanation is given at http://www.evilmadscientist.com/article.php/HomopolarMotor . After the wires are taken away the motor continues spinning but because there is very low friction; it is not being driven anymore. If you let it go long enough it will eventually stop.

QUESTION: ;
I think no object can travel any faster than whatever the force that pushes it travels. Like a bullet from the muzzle of a gun. I assume its greatest speed in its journey is at the muzzle of the gun. If true, and baseball pitchers routinely pitch 100 mph baseballs, how is it possible for the pitchers finger (s) to decelerate from 100mph in a space of what can't be more than a fraction of an inch in a fraction of a second. Seems like that would tough on any part of the body.

ANSWER:
Well, you should not think of a force as being something which has a velocity; it is simply a push or a pull. The velocity of something is maximized or minimized as determined by the acceleration which is determined, via Newton's second law, by the force. In your example of a bullet, the velocity is likely greatest just as the bullet leaves the barrel because there has been a large force acting on it and a small force acting against it (air friction). As soon as it leaves the barrel, the only forces on it are air friction (which slows it down in the direction it is moving) and gravity (which accelerates it in a downward direction). The pitcher example can be understood as follows:

The instant that the ball leaves the hand the hand must be moving with speed 100 mi/hr and, as you note, must experience a force to stop it.
But the hand does not stop in a fraction of an inch, it probably travels a couple of feet or more.
Understanding this you can see one of the reasons for "follow through" in throwing balls, golf swings, etc.
A rough calculation of the force is: let the time to stop be 0.2 s, the initial velocity be 100 mi/hr=45 m/s, the mass of the hand be 1/2 lb=0.23 kg, and the distance traveled be 1 m=3.3 ft. Then the average acceleration is 45/.2=225 m/s²=503 mi/hr/s. Then the average force is 225x0.23=52 N=12 lb. The source of the force on the hand is the wrist. Note that the distance does not factor into calculating the acceleration, just the change of speed and the time. The distance and time are not independent and making the distance larger makes the time larger which makes the acceleration and force smaller.

QUESTION:
Is there any type of matter which cannot be melted, even when heated?

ANSWER:
It depends on factors like the temperature and pressure. So there is no simple answer to your question. Many compounds will not melt for some pressure ranges but they will sublime, that is turn into a gas directly from the solid. An example is carbon dioxide (dry ice) which does not melt at atmospheric pressure, but it does sublime.

QUESTION:
How far would a person need to fall before they accelerate to their "terminal velocity." 100 feet? 500 feet? Higher? I'm told that terminal velocity is about 125 mph for a person free falling.....and that the acceleration formula is 33 feet/second/second. But I don't know how to reverse that math.

ANSWER:
What the terminal velocity is depends on a number of things including the skydiver's weight, the density of the air, and how he orients himself relative to his fall. If he orients in a belly flop position he will have a lower terminal velocity than if he falls feet first. Also, he technically never reaches the terminal velocity but just approaches it asymptotically. But you can estimate when he is within, say 95% of the terminal velocity. The details of the physics are given in a previous answer; I will just give you the results for your situation here. Choosing the mass to be 100 kg (about 220 lb), the air density to be 1.3 kg/m³, cross sectional area to be 1 m² (more like the belly flop position), and the drag coefficient 1.2, I find a terminal velocity of about 35.4 m/s (about 79.4 mi/hr). The characteristic time is about 3.6 s; this is the time it takes the speed to go to about 76% of the terminal velocity. If you wait twice the characteristic time, about 7.2 s, you will reach about 96% of the terminal velocity. The characteristic distance is about 64 m; this is the distance it takes the speed to go to about 63%. If you go three characteristic distances, 192 m (about 630 ft), you will reach about 95% of the terminal velocity. If you are interested, the characteristic time is v/9.8 s and the characteristic length is 19.6/v² m where v is the terminal velocity in m/s. It is interesting to note that cats that fall out of skyscrapers usually survive because their terminal velocity is slow.

QUESTION: ;
How can motion be generalized by simply looking at an objects velocity and acceleration. More specifically, why do we only use the first two derivatives of distance to explain the change of distance? Why don't we consider higher order derivatives? Wouldn't an inclusion of these higher order derivatives be necessary to fully account for motion? The question is "Why can we generalize changes in distance by looking only at two derivatives of distance?"

ANSWER:
Actually, you don't really need anything but the position as a function of time to know everything there is to know about the motion of a particle. Once you know that, just differentiate it to get the velocity which is the rate of change of position. If you care to know the rate of change of velocity (acceleration), differentiate the position twice. If you wish to know the rate of change of acceleration (which engineers often do and call "jerk"), differentiate the position three times. If you want to know how the jerk changes, differentiate four times. And so forth. But every bit of this information is contained in the position as a function of time. Physicists are normally only interested in velocity and acceleration because, among other things, Newton's second law (N2) says that a force causes an acceleration. It turns out that accleration is not a useful quantity in the theory of special relativity since N2 in the form F=ma is actually not correct in relativity.

QUESTION:
Do electrons maintain a standard orbit about the nucleus?

ANSWER:
Actually, the idea of electrons being in well-defined orbits in an atom is just a pictorial way to qualitatively understand atomic structure. Originally Niels Bohr solved the puzzle of how atoms are constructed but his ideas later evolved into a much more complete theory of atomic structure. An atom consists of "clouds" of electrons around the nucleus, that is the electron does not maintain its identity as a point particle but becomes "smeared" over the volume in a way which is determined by the properties of the "orbital" it is in. This is quantum physics. However, if you say that the shape of the cloud represents the orbit, then, yes, electrons in one atom have the same distribution as in any other atom of the same element.

QUESTION:
Hypothetical situation: I'm walking in the park. Then, the earth explodes, casting the fragments of earth to outer space. Not unlike the big bang. Now, I am smack dab in the middle of one of those fragments. What is the cause of my death? Will my tendency to remain unmoved turn me into a meat puddle? Or will some other force counter act that so that I die from the loss of atmosphere and loss of oxygen (I doubt this)? From freezing (I doubt this too)? Your help is great appreciated as to what method in which I would die, and about how long my existence will be from explosion to death.

ANSWER:
The fragment you are on suddenly experiences an enormous acceleration as a result of the enormous force it experiences. It pushes outward on you to give you the same acceleration, so it must push on you with an enormous force, far more than your body is designed to survive. It is basically the same as your hitting the ground with a very high speed (like after jumping from a tall building)--the huge acceleration of your stopping requires a force and that force kills you.

QUESTION:
If I heated my oven to something like 500 deg F, and it was a perfect insulator, would the temperature inside eventually decrease due to irreversible processes such as friction between gas molecules and possible deformation from molecular collisions?

ANSWER:
By definition a "perfect insulator" will not let any energy out. We never talk about friction between two atoms or molecules since it is a macroscopic phenomenon resulting microscopically from interactions between molecules. In this context if one molecule gains energy in a collision the other mus lose exactly the same amount. I do not know what you mean by deformation, but at normal temperatures the only excitation possible is rotational excitation and this is already included in the microscopic description of the hot gas. So, the temperature will not change.

QUESTION:
I recently read an article about "nothing" in the center of the universe. Since the "hole" is 5 to 10 Billion light years away, how long would it take to get there using current technology (such as the fastest man-made object: 250,000 km/h) and in a space craft traveling at 99% of the speed of light? Also what would be the relativistic age difference (earth vs spacecraft observer)?

ANSWER:
(I will take the 10 billion light year distance; everything is half as large for 5 billion light years.) The first velocity you quote, 250,000 km/hr is about 0.00023=0.023% the speed of light, so both observers would see the same elapsed time which would be 10x10⁹/2.3x10^-4=4.3x10¹³ years, about 43,000 billion years. The case of a speed 99% the speed of light, we would see it take about 10 billion years (just a hair longer) but the observer in the space craft would see much less time elapse. He would see the distance to the hole to be contracted to 10x(1-.99²)^1/2=1.4 billion light years; so the time it would take him, according to his clocks, would be 1.4/.99=1.42 billion years.

QUESTION:
An acquaintance and I are having a heated discussion relating to the 1960 jump from 103,000 ft from a gondola by Joe Kittinger. According to several reports, Kittinger reached speeds over 600 MPH after he jumped. Since I can't prove that he did, I'm no physicist, he believes he must be correct. How can I determine the speeds that were reached in this jump?

ANSWER:
In principle, this is a simple free fall problem. In practice, we need to worry about air resistance since that becomes important in real life at high speeds. However, there is very little air above about 60,000 feet, so let's assume that there is no air resistance and see how far he has to fall to reach a speed of 600 mi/hr and if it is less than about 40,000 feet he probably achieved that speed. The acceleration due to gravity is about 21.8 mi/hr/s; that is a freely falling object will gain about 21.8 miles/hour as each second clicks by. One pertinent physics equation is v=at where v is the speed (assuming we start from rest), a is the acceleration, and t is the time. So, putting 600 in for v and 21.8 in for a we can solve for t: t=27.5 s; in other words, after about a half a minute the object will be going 600 mi/hr. The second pertinent equation is s=½at² where s is the distance traveled in time t. Solving for s I find s=12,000 ft, that is he will have a speed of 600 mi/hr when he is at about 90,000 ft, still far above where there is signficant air. (Incidentally, in the second calculation I used a=32 ft/s/s so the units would come out right, viz. feet.) So, I would say that yes, he must have gone at least 600 mi/hr. I did a little research and saw 714 mi/hr quoted as the highest speed he achieved. Once he starts encountering significant amounts of air he will begin slowing down.

FOLLOWUP QUESTION:
This is a follow-up, and didn't know if I should post it online or not, since you've already answered it. But, the person with whom I'm having this discussion still insists you're answer is wrong. He fancies himself smarter than a nuclear-physicist, I guess, and, by his calculations , the top speed that Kittinger could have reached is 350 mph. Here is his argument and his calculations, referring to your response.

"That's just a repeat of what the other professor said, and in both cases they conveniently ignore drag. If you're going to ignore drag then ignore it and the guy keeps falling at increasing speed. Why stop accelerating at the point that corresponds to what the claims are? When you plug the drag variables into NASA's algorithm Kittinger doesn't get to 614mph. The professors don't bother to verify that the air is too thin to have any effect. Tell the college professor's to go to the Chemical Engineer's Handbook and look up Fluid and Particle Dynamics. In there is a table that describes the activity of bodies in free fall through a fluid. When they're going slow, they are stable. As they increase in speed they first start to tumble erratically, then they start spinning about their axis of least inertia. The tumbling starts somewhere around Mach 0.4 and the spinning around Mach 0.6 That's the flat spin the story eludes to, and the college professors ignore. If he fell at 614mph he's at Mach 0.9 and is in a flat spin. The big problem is all the contradictory statements that are attributed to Kittinger. He the first supersonic skydiver. He gets to an estimated 614 mph or 714. He has no sense of speed, yet he knows he keeps accelerating after the drag chute opens. That chute opens at 13 secs, or 16 secs or at 96000 feet. First of all drag doesn't work like a break. A body sitting still has no drag. As it speeds up drag increases and keeps increasing until the force propeling the object and the force of drag are equal. Then the object stops accelerating and moves at constant speed as long as force and drag stay the same. Drag is related to Velocity(speed) by the drag equation. D = 0.5 x Cp x p x A x V^2 So as long as you keep the Cp,p, & A the same, there is one value for drag for every value of speed (V) I'm not going into all the other crap, but the force pulling Kittinger down and causing him to speed up is gravitiy working on his weight. At roughly 300 lbs it takes 300 lbs of drag to stop him from accelerating. He's the shape of a brick, roughly half as wide as long and 1/3 thick as long. The Cp of a brick is 2.1. We use that to compute air flows through our tunnel kilns at the brickyard. The density of the air is about 0.00004 slugs/cuft. He is exposing about 15 sqft of area to the "wind". So if we plug in all those numbers in the Drag equation and solve for V(speed), he stops accelerating at 690 fps or 470mph. I'd say the air is thick enough to make a difference. But that doesn't take into account the drag on the small parachute he deployed to keep himself from going into that flat spin. It's 6' in diameter that's 28.26 sqft of area. The Cp for a round chute is 1.5. So as long as the drag on the chute and the drag on Kittinger doesn't total 300 lbs or more he is still accelerating. At 13 secs the total drag is 254lbs and his speed is 283 mph. He'll accelerate for less than a second more and get to about 290 mph. At 16 seconds the total drag is 384 lbs, so he'll decelerate from 347 mph with a pretty good jerk. I have no idea where or why the 96000 ft comes from, so I'm going to ignore it. He supposedly used a timer to deploy the chute. The speed of sound is around 660mph and tumbling would start somewhere around Mach 0.4 which is 0.4 x 660 = 264mph. That's damn close to the 13 sec mark. We'll never know based on the info available, but I don't think he got over 300-350mph."

Here are the facts, as presented in an article at http://www.centennialofflight.gov/essay/Explorers_Record_Setters_and_Daredevils/Kittinger/EX31.htm
1. Kittinger jumped from 102,800 ft.
2. His weight is approximately 300 lbs.
3. He was falling in a backward orientation
4. After falling for 13 secs, a small chute, 6 ft. in diameter, opened.
5. He feel for 4 min. and 36 secs more bringing him to 17,500 ft.

ANSWER:
Your friend certainly makes some quite good points, although he is maybe a bit overemotional and maybe a little hostile to us college professors. It is true that we often simplify problems to get to the core of a problem. So let me be a little more careful and go over the calculation of your friend the way I would do it since some of the numbers he quotes are undocumented and some of them (in particular slugs/ft³) are completely incomprehensible to a modern physicist! Your friend must be an engineer. His equation is quite correct, that is the terminal velocity is given by v=[(2mg)/(rAC_p)]^1/2 . Now it is easy to see how disputes can arise because the answer, of course, depends the choice of constants some of which are not easy to estimate (for example, I would say approximating the man as a brick is what some nutty college professor might do). The density of the air at 100,000 ft is about 1/100 the density at sea level and, since the density at sea level is about 1.3 kg/m³, I will take r=1.3x10^-2 kg/m³. I searched the web for tables of drag coefficients and found that a parachutist has C_d=1-1.4 (not 2.1 as your friend assumed); I will use 1.2. The cross sectional area also requires a rough estimate since it depends on whether he is falling, for example, feet first or is falling "belly flop" orientation. I will assume the latter so as to get as small a speed as possible and I will estimate the area as about A=2 m x 0.5 m=1 m² (your friend uses 15 ft², about 1.4 m²). Using m=136 kg (300 lb) and g =9.8 m/s², we are ready to estimate v; I get v=413 m/s= 924 mi/hr.

But, there is important information which you did not tell me the first time through--the opening of the small chute. So now the cross sectional area is about 2.5 m² and the drag coefficient is about 1.42 (I model it as an open hemisphere into the wind). So now I get a reduced terminal velocity of v=240 m/s= 537 mi/hr.

Now I have the terminal velocities, what happens in our specific example? The space is too limited here to put in all the details, but I have assumed a constant density for the first 4000 m (about 12,000) of fall. I went back to an intermediate mechanics book to find the dynamic analysis of the falling body with quadratic velocity dependent drag force and I could apply (knowing the terminal velocities from above) the analysis to this specific problem. In the first 13 seconds I find that he falls about 1000 m and ends up with a speed of 130 m/s (291 mi/hr). Then, after he has fallen 3000 m more he will have a speed of 208 m/s (465 mi/hr). But he is still accelerating but now the air gets denser so his acceleration decreases even more; nevertheless, as he falls, since he is still fairly far below terminal velocity (240 m/s) he will end up going faster than 465 mi/hr.

So who is right here? Well, your friend is right in that we will never know based on information we have. I can easily imagine that I have made a factor of two error in the density, the area, or the drag coefficient (and so could your friend); increasing all by a factor of two would reduce the terminal velocity by almost 2/3 which is the difference between 600 mi/hr and 200 mi/hr. The results are too sensitive to modest changes in the parameters.

QUESTION:
At our work we have gone stupid over GREEN Issues, we have been instructed to turn off the hand dryer at the wall plug when our hands are dried, thus saving some of the blow cycle. Now when you dry your hands you turn it on at the plug, get the remaining part of the last cycle and then have to turn the blower on by the big silver button on the dryer. Are we saving enery at all or is "turning on/starting the dryer" the big user of power? Thus it would be better for it to finish its cycle each time

ANSWER:
It is not true that turning an electric appliance on and off uses more energy. (It is also not true that turning a car off and back on at a long traffic light consumes more gasoline than running the whole time.) Electric heaters like your hand dryer are among the worst energy hogs so running them only as long as necessary to dry your hands does make sense. However, if your employer is really serious about energy conservation, he would uninstall the electric dryers and replace them with paper towels or, even better, one of those machines which has a long cloth roll which is simply washed and then reused when it is all used up.

QUESTION:
Compressing gaseous nitrogen makes liquid nitrogen which is very cold. But compressing things makes them hotter. Any help alleviating my confusion will be greatly appreciated.

ANSWER:
The compressed gas does get hot, but that is not the end of the process. Here is a link with an explanation.

QUESTION:
This question has to do with television signals emitted from this planet. If there is a star that is say exactly 40 light years from us, how weak would our "electromagnetic reflection" be from the star or a planet (I'm assuming a reflection is possible?) by the time we get it back, some 80 years after it left? I realize that probably not all stars would reflect equally, so my question is geared toward whether there might be anything at all that could be measured and analyzed someday.

ANSWER:
Almost anything will relfect electromagnetic radiation. The real problem here is the intensity. The intensity of radio waves emitted from the earth will fall off approximately like 1/r² where r is the distance. So, if you have a certain intensity 1,000 miles from earth, the intensity 1,000,000 miles away will be (10⁶/10³)²=1,000,000 times weaker; and 1,000,000 miles is a very small number compared to the distance to a star. And the reflected signal will lose just about the same fraction coming back. My guess is that the intensity would be so low that no information could be obtained from it.

QUESTION:
If an object is completely submerged in water (let say sitting on the bottom of a lake) why does buoyant force help you to lift the object out of the water. What I'm confused about is why the pressure of the water pushing down on the object doesn't hurt you as much as help you?

ANSWER:
Let's think of it as a box. The bottom of the box experiences a force due to the pressure in the water which pushes up. The top of the box experiences a force due to the pressure in the water which pushes down. But the force on the bottom is bigger in magnitude than the force on the top because the pressure gets bigger as you go deeper. Therefore there is a net upward force on the box which we call the buoyant force.

QUESTION:
What is the speed of gravity?

ANSWER:
This quetion has been previously answered.

QUESTION:
How would i calculate the number of grains of sand on Earth ???

ANSWER:
There is, of course, no way to calculate it. You could estimate it, however. I am not a geologist, so I really don't know how much sand there is in the world but it must be a lot. I will take a wild guess that there is enough sand to cover the entire earth to a depth of 10 cm =10^-1 m (there is probably more than that). The surface area of the earth is about 5 x 10¹⁴ m² (from A=4pR²) so the total volume of sand is about 5 x 10¹³ m³. Now, I will guess that a typical grain of sand would have a diameter of maybe 0.1 mm=10^-4 m so the volume of a typical grain of sand would be about 10^-12 m³. So the number of grains of sand would be the ratio of the volumes (volume of sand/volume of one unit of sand), about 5 x 10²⁶, quite a lot! This is comparable to about how many atoms there are in your pencil.

QUESTION:
during the double slit experiment, i understand the bright patches are caused by the peak of one wave interfering with the peak of another to form a doubly high peak. but when the bottom of two waves also interfere with each other to produce a doubly low wave, does this also produce the bright patch?

ANSWER:
Every point on one wave interferes destructively with the corresponding coincident point on the other wave.

QUESTION:
One of my classmates claimed during our study group that if you glue two permanent magnets together, north to north that eventually they will reverse poles… is this true?

ANSWER:
What happens depends on many things like the materials from which each magnet is made, temperature, how strong each magnet was, etc. One thing is for certain, though: they will not both reverse their polarities. Either neither will or one will or both will become demagnetized.

QUESTION:
Let's say I have a metal rod about a half an inch thick and 300,000 kilometers long. Then say I give one end of said rod a mighty whack with a hammer, propelling it forward by one inch in a mere fraction of a second. My questions is, wouldn't the impact of my hammer cause the other end of the rod to move forward one inch just as rapidly as the end where I whacked it? And would this violate Einstein's law that states that nothing can move faster than "C"? Or would the far end of the rod have to wait one second after my whacking my end before moving forward by one inch?

ANSWER:
Have you thought about the implications of your question? I figure the mass of the rod would be about 10¹⁰ kg. Suppose that you exert a constant force such that after 0.1 s it is moving with a speed of about 0.5 m/s; it would have moved about an inch in this time. The force is the change in momentum divided by the elapsed time so, roughly speaking, the required force is about 10¹² N. Where are you going to get such a force? Anyhow, to the meat of your question: no, the other end would not start moving instantaneously. It could not begin moving until at least one second later than your end started moving for the reason you state: no information can travel faster than c. In reality, it would be much longer than one second because your "mighty whack" will compress the rod and this compression will move with the speed of sound in the metal and this compression is what travels to the other end to move it.

QUESTION:
If I were to stand on the moon with my head facing directly forward into the line of orbit, would I weigh more than if I were standing on the exact opposite side of the sphere, in the rear so to speak? In other words, does the movement of a planetary object either add or subtract from one's mass depending on where they might be situated?

ANSWER:
Your weight is the force which you experience due to the gravitational field you are in. Assuming the moon to be a homogenous sphere, your weight is independent of where you are on the surface and of the motion of the moon. Your mass is the inertia you have in your rest frame and it is independent of everything. Rest mass is an inherent property of an objece, weight is determined solely by mass and field.

QUESTION:
Given that gravitation and acceleration are locally indistinguishable, and that "gravity" is causing the light to bend in gravitational lensing, can acceleration also cause gravitational lensing in some aspects?

ANSWER:
Suppose that you are in an accelerating elevator with a hole drilled in the side; if a beam of light enters parallel to the floor, you will see it follow a parabolic trajectory as it crosses the elevator. So the answer is, yes, light bends when observed from an accelerating frame of reference.

QUESTION:
Given initially that a Powerful large magnet and a heavy soft iron are attached magnetically to each other , we obviously have to expend a lot of ENERGY to separate it away from each other. But by law of conserv. of energy and E=MC^2 ,should the soft iron(or magnet) initially attached to magnet (or iron) weigh more? If not where is the energy we expended? if so it is unclear where we should bring relativity to solve it. (Same can be asked with gravitationally strong object.But it would bring Gen.Rel into question, which would be uncomfortable for this simple question)

ANSWER:
Yes, the magnets will be more massive after you have separated them. But, the amount will be unmeasurably small. Suppose that you do 100 J of work to separate them. Then the mass increase will be Dm=100/(3x10⁸)² kg, about 10^-15 kg!

QUESTION:
If an object weighing 500lbs (let's say an elevator) falls from a height of 1,000ft (without any resistance other than air) and hits the ground (concrete), how much energy would it be equal to. And if you would, please translate into sticks of dynamite.

ANSWER:
The energy when it hits the ground is about 680,000 J which is equivalent to about 0.16 kg of TNT.

QUESTION:
Whats the lowest Temperature ever attained here on earth according to latest details ?? .Some unconfirmed source told me that it was less than a millionth degree above 0 kelvin

ANSWER:
The lowest temperature I have found reference to is 100 pK. That is one ten billionth of a degree Kelvin.

QUESTION:
often aluminum outboard props bend and warp, the manufactures answer is that over trimming the engine so that it sucks air down into the props vortex, the air becomes traped, supper heats and then warps or melts the prop. wouldnt that trapped air have to reach 660 degrees to melt the prop? is that even possible?

ANSWER:
The prop is not being melted, just warped. At high temperatures metals become softer, more easily deformed (that's why the village blacksmith had a hot fire).

QUESTION:
To our eye + brain, a material has color when it absorbs all wavelengths of the visible spectrum and reflects 1 wavelength. For example, a red brick has color because it absorbed visible light and reflected light with the wavelength associated with the red color. Why did all the other wavelengths of light get absorbed and the red light not get absorbed? Are all wavelengths absorbed and the red color wavelength is radiated? Does this have anything to do with the HOMO-LUMO Gap (chemistry)?

ANSWER:
Of course, your explanation is a little oversimplified. Nothing absorbs everything except one wavelength. A red brick absorbs more of the light in the shorter wavelength (blue) end of the spectrum than in the longer wavelength (red) part of the spectrum. But your general idea is right. What gets absorbed is determined entirely by the properties of the molecules in the material, it is an atomic-level effect. All molecules have absorption and radiation spectra and they vary from material to material. I have no idea what the HOMO-LUMO gap is.

QUESTION:
Light, radio signals, and audio are all types of waves which can be measured in Hertz. I know that what we hear (audibly) are compressions of air created by the wave (let's assume for this question we have an audio wave of 900Hz). Light is also a wave, lets choose yellow which would be 515THz ( terahertz ). Considering this, light can travel accross empty space (obviously) as a wave. Here is where I find a problem that I want answered: If a 900HZ wave were created from a source in space (not as sound, just a 900hz wave) and was directed toward earth could we (on the earths surface) detect the 900hz signal? If so how, wouldn't this cause sound compression when it reached our atmosphere, making it audible? If not then why, 900hz is a wave just like 515THz, is it possible to have a 900hz wave that you can't hear on the surface of the Earth with air? Or If 900hz can not travel through space then why can a lightwave (or whatever wave) travel through space at 515THz but a 900Hz wave cannot, radio and lightwaves do not require the presence of air to travel through space? Unless there is another possibility I have not thought of above, all the options seem contrdictory to what I Understand about physics, sounds waves, etc... I am by no means a scientist or even a physics student, just a pondering thinker.

ANSWER:
The whole key is "what is doing the waving". For sound, as you note, it is the air. For electromagnetic waves (radio, light, xray, gamma ray, microwave, etc.) it is electric and magnetic fields. You can hear compression waves in the air but you cannot hear electric or magnetic fields. Your eye can detect electromagnetic waves in a narrow frequency range and we have instruments to detect other frequencies. Hence, if the 900 Hz wave came across space then it must have been electromagnetic so you could not hear it but you could detect it with an appropriate antenna and electronic receiver. By the way, the wavelength of such a wave would be about 333 km.

QUESTION:
Hi I'm a 52 year old high school teacher and this is a problem I could not solve in the new curriculum. Here it is, word for word:

A red ball is stationary on a billiard table OABC. It is then struck by a white ball of equal mass and equal radius with velocity u( -2i + 11j ) where i and j are unit vectors along OA and OC respectively. After impact the red and white balls have velocities parallel to vectors -3i + 4j, 2i + 4j respectively. Prove that the coefficient of restitution between the two balls is 1/2.

ANSWER:
First, allow me a little rant! It is utterly ridiculous that this problem is part of a high school curriculum. Coefficient of restitution (COR) is one of the least important concepts in classical mechanics. Furthermore, it is nearly always defined in terms of a one-dimensional collision which the collision in your problem is not, so it looks like the problem writer is trying to confuse the reader (which I consider to be poor educational method). Furthermore, I find that I do not get 1/2 for the coefficient of restitution when I work the problem. I will outline the solution to the problem and give my results. You can reconstruct the solution and see if I have made any errors. First, the COR e is related to the energy loss Q in the collision by Q=½mv²(1-e²) where m=m₁m₂/(m₁+m₂) (reduced mass) and v is the incident velocity (if one of the two particles is at rest as it is here). It makes no difference what the actual masses are since they are equal, so I shall choose m₁=m₂=1 kg such that Q=31.25(1-e²) J. (I have used v²=125 m²/s² as given in the problem.) Now, just calculate Q to get e. The information given about the recoiling velocities is their directions, not their magnitudes; to get the speeds you must do momentum conservation. The red ball moves at an angle of 53.1⁰ above the negative x axis and the white ball moves at an angle of 63.4⁰above the positive x axis. Conserving momentum in x and y directions I now find the speeds of the red and white balls: v_r=7.5 m/s and v_w=5.59 m/s. Hence the energy after the collision is 43.75 J and before the collision 62.5 J, so Q=18.75 J. Solving now for COR: 18.75=31.25(1-e²), e=0.63, not ½.

There is actually another way you can do it: if you work in the center of mass system it essentially looks like a one-dimensional collision since the two particles after the collision move colinearly apart with speeds of 3.54 m/s each so that the speed of separation is 7.08 m/s and the speed of approach before the collision is 11.18 m/s. The COR is defined as the ratio of the speed of separation over the speed of approach which works out to, you guessed it, e=0.63! Now I have more confidence in my solution.

QUESTION:
what, if any, would be the major 'noticeable' differences in the universe if the speed of light were drastically higher, say 10x, 100x or 1000x?

ANSWER:
For starters, you would not be here to ask this question. The existence of life as we know is very sensitive to the values of the most important physical constants, the speed of light, c, being one of them. The easiest way to see dramatic effects is from good old E=mc². If c were 10x bigger, the energy equivalent of mass would be 100 times greater, so the energy being produced by the sun would be 100 times what it is; talk about global warming! Assuming that protons and electrons still existed you could still have hydrogen since atomic physics is not very affected by relativity, but when you tried to make a nucleus you would find that the masses of the nuclei were very much less than the sum of its components due to the enormous binding energies. In fact, I do not think you could have a neutron so you could make no nuclei and therefore you would have no chemistry and the stars would not be able to make energy using fusion.

QUESTION:
What is the basic physics behind laser cooling.

ANSWER:
The basic physics is essentially momentum conservation. If a ball is moving toward you and you shoot it with a bb gun, the ball slows down (cools) a bit. Many collisions with bbs will slow it down more. In laser cooling, the ball is an atom and the bbs are photons from the laser. A nice simple explanation can be seen here.

QUESTION:
Given COMPLETE information about Hydrogen and Oxygen and Using physics laws "as it is now" to its full extent (forgetting about the mathematical and Quantum mechanical complexities) can we basically "predict" how a combination of type H2O out of these gases behave? for example ,"Predict" that such a material would be liquid under room temp. and has 1Kg/cc density, etc etc.?(we can dispense with all other branches of science and make physics "universal"

ANSWER:
When you say to forget about "quantum mechanical complexities" you guarantee that the answer to your question is no. However, "complete information" really means detailed wave functions of hydrogen and oxygen atoms; given that information, excellent predictions of the properties of H₂O may be calculated.

QUESTION:
I was wondering why increasing the distance between the plates of a parallel plate capacitor (when it's charged and not connected to a circuit) increased the Voltage. I realize that since this decreases the capacitance and the charge remains the same then by then equation Q=CV the voltage must increase. But logically this doesn't make sense to me. Since the equation for voltage is V=kq/r, this would imply to me that as you increased the distance between plates you'd also be increasing the distance between charges. Thus I would think voltage would decrease.

ANSWER:
The voltage you quote is for a point charge, not parallel plates. For parallel plates the electric field E is uniform and so the potential difference is V=Ed where d is the spacing between the plates. The field is determined by the charge Q on the plates and the area A of the plates, E=Q/(e₀A) so the field stays the same when the plates are separated.

QUESTION:
Which weighs more. There are two identical water bottles both are filled with the same amount of liquid water. One is then frozen. Both bottles arer taken on a hike. The dew point is such that the frozen bottle starts to form condensation on the outside. Will the frozen bottle endup weighing more due to the condensation that forms on the frozen bottle ?

ANSWER:
Freezing the water will not affect its weight so both bottles will weigh the same after one has been frozen. So, the condensation will cause the cold water to be heavier. [A technicality: because E=mc², the frozen bottle, because energy has been taken from it to cool and freeze the water, will actually be lighter. However, the amount by which it will be lighter will be unmeasurably small, so it may be ignored. A rough estimate: suppose that 1,000 J of energy are removed in doing the freezing; the mass equivalent is 10³ J/(3 x 10⁸ m/s)² which is about 10^-14 kg!]

QUESTION:
This is a question that's bugged me for a long time. If you can shine a light into a hollow perfectly smooth, reflective sphere with no means of the light escaping that sphere - is any sort of energy built up within?

ANSWER:
There is no such thing as a perfectly smooth, perfectly reflective surface. If there were, energy would build up inside the sphere.

QUESTION:
I understand that the speed of light is a constant, ie it is always the same in all circumstances. I have also been taught that refraction is caused as light hits a substance, through which it can pass, at an angle and is slowed. The lower part of the wave hitting before the upper, relative to the surface, and slowing causing an angle in the lights path.. So which is it, is light actually slowing when it travels through a substance or not?

ANSWER:
The law is that the speed of light in vacuum is the same for all observers. Light, when passing through matter, moves slower.

QUESTION:
Real life question: Tire pressure on and off the car: I am getting a new tire for my car. While it's on the rack, they check the pressure and it's a perfect 32 psi. They put the tire on my car, then lower the 3000 pound car back down on it, and say see ya' later. I say,"Shouldn't you check the pressure while the weight of the 3000 pound car is down on it?" "Nah", they say, it doesn't change. That doesn't make sense to me. I actually asked this question to my brother who is a ultra-high vacuum physicist at Sandia Labs, and he didn't know. I also asked this question at the famous Cartalk.com forum and got laughed out of it.

ANSWER:
Here is the basic physics, the ideal gas law: PV=NRT where P is pressure, V is volume, T is absolute temperature, N is the amount of gas, and R is a constant of nature. Let's assume that T stays the same when the car is lowered off the rack. Now, presumably the volume of the gas in the tire decreases a little bit; therefore, the pressure must increase a little bit to keep the product PV equal to the constant NRT. However, the volume changes by a very small amount compared to the total volume of the tire, so for all intents and purposes (but not exactly) "it doesn't change".

QUESTION:
If you consider a rock hanging from a two vertical massless ropes with a symetrical wieght distribution, and the system is staionary, is there anyway possible that the tension in the ropes will be greater than or less than half the weight of the rock?

ANSWER:
It depends on where the strings are attached to the rock. If one is directly above the center of mass, it will carry all the weight and the other will have zero tension. If they are equal horizontal distances from the center of mass, each will carry half the weight. The thing is that the sum of all the torques about the center of mass must be zero. So T₁d₁=T₂d₂ and T₁+T₂=W. where d is the distance of each string horizontally from the center of mass.

QUESTION:
How does High voltage transmission of electricity through long distances helps in reducing the energy loss during transmission?

ANSWER:
The power P dissipated in a resistor R is P=IV; if you increase the voltage and keep the power the same, the current becomes small. But, in the transmission line, if you use Ohm's law V=IR, P=I²R, so low current means low power loss.

QUESTION:
By the phrase "High Tension wires" what should we asssociate the meaning for "Tension"? Frequency (Hz) ? Volts ? Current strength? (Amps)?

ANSWER:
The voltage is high. The current is low. The frequency is 60 Hz.

QUESTION:
I have a question concerning a dream I had when I was 12. Now I am 22 but I just thought of it again. I'm not much for math, but this question has more to do with physics and the rules of the universe. So, my dream was about Jimminy Cricket of "Pinocchio" fame sitting on the Jolly Green Giant's shoulder while floating in the middle of outer space. In the dream the Green Giant was two light years tall while Jimminy was like an inch or two high. The question I woke up with was how long did it take each (Jimminy and the Giant)to see the Green Giants feet? Would it take both the Giant and Jimminy two years to see the Giant's feet? Is mass in anyway associated with the speed of time, with the greater the mass, the faster the time? I think that the Giant would be able to see his feet before Jimminy could. Sort of like how smaller moving objects, like insects, blood and obviously atoms appear to be moving fast for someone of human size, but does blood or an atom feel they are going ridiculously fast? I know that this question must have been asked and answered, but I don't know where to find the answer. And you guy's appeared in a google seach titled 'ask a pysicist.'

ANSWER:
The way you "see" something is to detect the light which came from it. Both the giant and the cricket, at any given time, see light which left the giant's feet 2 years ago. It makes no difference what the masses of the detectors are.

QUESTION:
The question deals with the center of gravity for a very specific object. Given a cylinder 12 inches in diameter and 8 inches long which is made of a homogeneous mass distribution; that has a 1.5 inch hole through it's center in the radial plane and is subjected to a uniform field. Viewed from the radial plane and aligned so as to see through the hole where would the center of gravity be? Viewed from the radial plane but orthogonal to the through hole where would the center of gravity be? I really don't need a specific numerical value but only to know if the center of gravity moves or does it stay located at the same place and is it the center of the volume?

ANSWER:
The center of gravity is independent of any external field and independent of how you view it. This object has the center of gravity on the axis of the cylinder and 4 inches from one end.

QUESTION:
Could antimatter ever be a threat to space travellers especially for space travelers within a solar system?

ANSWER:
Certainly not in the solar system since if there were any significant amount of antimatter we would certainly have observed its effects. There is also no evidence that there is a significant amount of antimatter anywhere in the universe. So, I would say, the answer to your question is no.

QUESTION:
I had a question about gravity. I have read that Einstein said gravitation is caused by geodesics and the tendency of mass to follow them. Is gravity a force?

ANSWER:
A force is something which causes an object which feels it to accelerate; so gravity is certainly a force in the classical sense. What is the origin of this force? That is what general relativity answers by saying that space is warped by mass, that is the gravitational force results from the geometry being altered by the presence of mass.

QUESTION:
I am a librarian assisting a library patron. The patron says at one time he had a book that gave him a formula to compute the weight of an object. If you put an object, such as a car, on a tire or ball or something that is pressurized, and you know the PSI, you can measure the size of the point of contact with the ground (the flat surface of the tire on the ground) and calculate the weight of the object.

ANSWER:
Consider a piston of cross sectional area A, vertical, which has a pressure P under it and a weight W sitting on it and everything is in equilbrium; for simplicity, neglect the weight of the piston itself or imagine it to have been absorbed into W. We must not forget that there is an atmospheric pressure P_a pushing down on the cylinder. Then Newton's first law specifies that the sum of all the forces must add to zero, and so PA-W-P_aA=0 (pressure time area equals force) so W=(P-P_a)A. But (P-P_a) is what is called the guage pressure, it is the pressure which most pressure guages read, the amount over (or under) atmospheric pressure. So 30 psi means, usually, 30+14.7 psi since P_a=14.7 psi. This seems to me to be equivalent to your question. Let's check it for reasonableness: suppose a car has each of its four tires in contact with the ground by an area of 6"x4" and the tire (guage) pressure is 30 psi. Then the weight of that car would be 6x4x4x30=2880 lb which is about what cars weigh.

QUESTION:
Is it possible to accurately measure the speed of a moving vehicle by just watching it?

ANSWER:
Well, I guess that depends on what you mean by "accurately" and what you mean by "watching it". In order to make an accurate measurement of speed you need to measure a time accurately and a distance accurately. Hence, if you know the distance between two landmarks and time the car from one to the other, its average speed is the ratio of distance/time. If you use your experience to judge the speed, I would call that estimating the speed not measuring it.

QUESTION:
If the moon were to leave earth orbit into space, what would be the effect(s) on earth .

ANSWER:
The most noticeable would likely be that the tides would nearly stop. Obviously, there would be no more solar (or lunar) eclipses. It is well established that many biological systems depend on the timing of the phases of the moon to time their functioning, but I am no expert on that. The moon also affects the precession of the axis of the earth, but this is a pretty small effect.

QUESTION:
what is the difference in brightness of three lamps if they are connected in parallel/series

ANSWER:
I assume they are identical. I will also assume that the light intensity is proportional to the power dissipated by the bulb; this is not a very good approximation because the resistance of tungsten wire is dependent on its temperature which is in turn dependent on the current through it. Then brightness depends on power which is proportional to V² where V is the voltage across the bulb. The bulbs in series will have only 1/3 the voltage across each as the bulbs in parallel, so they will be only 1/9 as bright.

QUESTION: ;
Is there a scientific proof that the atom is neutral?

ANSWER:
Basically you are asking if the magnitudes of the proton and electron charges are equal. Many very sophisiticated experiments have been done and the best results to date indicate that the charges are equal to an order of about 10^-21 where the magnitude of the electron charge is 1. In other words, you would have to go to at least the 21^st decimal place to see any difference.

QUESTION:
What keeps the protons and electrons together to form an atom?Gravity?Let`s speak on a simple atom of hydrogen.How can the proton+ which is 1840 the mass of the electron- be electrically balanced?

ANSWER:
The Coulomb force holds the atom together; this force is due to the electrical charges on the p and the e and those are equal but opposite in sign (there are two kinds of charge). Gravity is totally negligible in atoms and the relative masses of the two has nothing to do with the problem. Actually, that is not quite true: if a proton and an electron had equal masses they would orbit around a point halfway between them but this has nothing to do with gravity.

QUESTION:
The medieval model of the solar system, which places the earth at the center and the other planets (including the sun and moon, per the medieval definition of "planet") in orbit about it, is incorrect; however, if one makes a mathematical model of the solar system by, e.g., assigning a position vector to each object, and then subtracting earth's position from each object, one obtains what seems to be a consistent, working geocentric model. In fact, it vaguely resembles the less popular medieval model designed by Tycho Brahe.

Is there a reason that this model is inaccurate? It seems that the heliocentric vs. geocentric argument is really just a question of which reference frame should be preferred, when in fact there is no preferred reference frame. Granted, the geocentric model I have suggested is cumbersome and less useful for practical purposes, but it seems that it is accurate. Most people believe that the sun is at the center of the solar system and that ignorant persons of the past believed that the earth was at the center. It seems more appropriate to say that one can arbitrarily choose a center, and that ignorant people of the present think that the choice of center is important.

Am I wrong? I have been really curious to discover whether or not I'm just missing some important point.

ANSWER:
Suppose that you are in a very large rotating drum (they have rides like this at an amusement park sometimes). You perceive yourself as being pushed into the wall and if the drum spins fast enough you will be crushed by this "force". What is actually happening is that, because you move in a circle, you are accelerating even though your speed stays the same because the direction of your velocity is constantly changing. Because of Newton's second law, a force is required to keep you moving in this circle and the wall of the drum exerts a force on you to achieve this acceleration. Now suppost there is a man at rest standing in the center of the drum. He feels nothing at all. Now, you want to say, "Let's choose me as being at rest and the other guy going in a circle around me; that will be just as good a description of the situation." But, alas, as you can see, there is a world of difference. If two objects have constant velocity it makes no difference which you consider at rest, but if one is accelerating and the other is not, they are not equivalent. Finally, you know that the earth moves the way it does because there is a force on it by the sun; the sun feels the same force. But since the sun is so enormously more massive than the earth, there is no way this force could cause the sun to move in an orbit around the earth.

QUESTION:
Why gravitational constant cannot be determined accurately just like c=299792458 m/s.As far as possible this was the result-: G=6.6732 X 10^-11 in units -m^3 kg^-1 s^-2.

ANSWER:
There are several answers. First, since the meter is defined in terms of the distance light travels in a given time interval, the speed in m/s is, essentially, a definition and not a measurement. Still, in order to make this definition, the speed of light had to be measured very accurately in terms of the older definition of the meter. The speed of light (or anything) is relatively easy to measure accurately: if you have very accurate clocks and rulers you can measure a speed very easily. The gravitational constant, on the other hand, requires that you measure very accurately a mass (not too hard), a length (not too hard), and a force. But the gravitational force between two laboratory-sized masses, say a couple hundred kilograms, is very difficult because gravity is nature's weakest force. A group at the University of Washington has been performing innovative experiments for many years trying to improve the accuracy of G.

QUESTION:
Has any 2 (atleast) of the 4 fundamental forces been successfully unified just like electricity was joined to magnetism earlier?

ANSWER:
The weak interaction has been unified with the electromagnetic interaction; one refers to the electroweak force. The weak, electromagnetic, and strong forces have been unified into what is referred to as the standard model of particle physics. Gravity is the odd guy out.

QUESTION:
The law of physics are the same on every point of the surface of the planet Earth or not?

ANSWER:
If it is truly a law of physics, it is true everywhere in the universe.

QUESTION:
Please can you explain what happens to the energy released by the shattering of a glass on a hard surface? We are told that the energy on Earth has remained constant since the formation of the planet so what is the fate of the energy produced by this event?

ANSWER:
What makes you think energy is released? Why does a piece of glass not just spontaneously break? The fact is, you must put energy into the glass to make it break. If you drop it, it has kinetic energy when it hits and then the surface does work on it by exerting forces on it. So the question should be what happened to the energy which got put into the glass to break it. It takes work (energy) to break molecular bonds which were holding the glass together before it broke; there goes some of the input energy. It makes a big crash; there goes some more of the energy (sound). It will heat up a little bit; there goes some more of the energy.

QUESTION:
What sort of interaction between the atoms and photons makes them to be reflected (bouncing of the mirror) and/or refracted (like through diamond) ?.If the answer involves quantum mechanical implications does that pose any limitation to the possible making of perfectly reflective mirrors?

ANSWER:
Photons interact with electrons via the electromagnetic force. However, it is much more fruitful to understand reflection and refraction by considering light as waves. Then, whenever a wave encounters a medium of a different index of refraction (that is the light travels at a different speed) it has the possibilities of either reflecting or refracting. The amount of each depends on numerous things, particularly angle of incidence, both indiexes of refraction, and polarization. There already is a perfect mirror which is total internal reflection which is used for fiber optics for example. (Please note that I say "perfect" in a hypothetical way since no surface is perfectly smooth and all media absorb light, so no reflection is really 100%.

QUESTION:
Fusion of (ionized) hydrogen molecules is done by increasing their temperature AND squeezing them using powerful electromagnets.(right?). If so, is it possible to "FUSE" them under normal room temperature just by indefinetly increasing the electro-magnetic force?. If so possible, what about "FUSION" under temperatures near 0 Kelvin ?

ANSWER:
The magnetic fields are not to "squeeze" them but to confine them. The high temperatures are required so that the positive ions have enough energy (that is enough speed) to overcome the electric repulsion from other positive ions. They need to get close enough to feel the nuclear force for fusion to occur and slow ions cannot do this. Furthermore, magnetic forces are perpendicular to the direction of motion so this force cannot squeeze; also, the magnetic force is proportional to the speed of the particle, so the slower the particle is moving (cold) the smaller any magnetic force is.

QUESTION:
Are there any acceptable alternatives to the current Big Bang model of the Universe? What are they? What is the best evidence for the Big Bang model?

ANSWER:
I know of no reputable astrophysicist who would not accept the big bang as the only viable theory of the beginning of the universe. This is not to say that there are not problems (like where did all the energy come from?). The best evidence for the big bang are the microwave background and the fact that the universe is observed to be expanding out from a single point. A more interesting question to most astrophysicists than the birth is the ultimate fate of the universe; answering this question involves the currently fashionable topics of dark matter and dark energy.

QUESTION:
SIr why does gravity so different from other forces that it doesn't depend on the mass of the object where the gravitational force acts?

ANSWER:
I guess you are asking why all objects have the same gravitational acceleration; the reason is, simply that the acceleration is inversely proportional to the mass but the force is proportional to the mass and so mass cancels out. See an earlier answer for more details.

QUESTION:
am a member of a group of people with an interest in space & the universe. We have been having a debate that is no closer to being solved than when it first arose. This is topic being debated: If an alien race were to live on a planet several light years away from Earth, we know that Earth would look like a star in their night sky. We also know that the light they saw would've left Earth many many years ago; perhaps even when the dinosaurs lived. If they were to have a telescope SO powerful that it could zoom in on the living animals on the surface of Earth, would they be zooming in to see the animals of present-day Earth? Or, would they be looking at the dinosaurs? I would VERY much appreciate if you could help us in finally putting this debate to rest.

ANSWER:
To see something, your eye (or telescope) must detect light which was emitted from that object (or reflected from it). So, when you look at a friend who is 100 m away, you are not seeing him as he is right now but how he was 100/3 x 10⁸=3.3 x 10^-7s ago. 1/3 of a millisecond is a quite measurable time. Now suppose you are on a planet which is 100 light years from earth. When you see the earth you are seeing as it was 100 years ago because a light year is the distance light travels in a year. The moon is 1.3 light seconds from the earth and the sun is 8.3 light minutes from the earth. So, when you see the moon you are seeing it as it was 1.3 seconds ago. If the sun were to blow up right now, you would not know it for 8.3 minutes.

QUESTION:
Is there a thought experiment that shows (we can deduce from it) how mass increases at relativistic speeds just as there's plenty of such to show how coordinates transform?

ANSWER:
I am not aware of a simple explanation such as those used for length contraction and time dialation. In fact, there is no particular need to even say that mass increases; what you must do is redefine momentum such that momentum is conserved for an isolated system and one possible interpretation of this redefinition is that mass increases. See my earlier discussion of this topic.

QUESTION:
In the phenomenon of polarisation, when a ray of light is passed through a crystal, the ray splits into two, on the basis of the direction of vibration. How is it possible when the light is a combination of electric and magnetic vectors vibrating in mutually perpendicular direction?

ANSWER:
An unpolarized beam of light has electric fields pointing in random directions; for each ray there is also a magnetic field normal to the electric field. Light which is polarized has all electric fields pointing in the same direction and all magnetic fields are perpendicular to the electric fields. It is convention to choose the direction of the electric field as the direction of polarization but the magnetic field is still perpendicular to that direction. The phenomenon you cite is called birefringence and the split beams have different polarizations.

QUESTION:
why do the astronomers say that viewing an event like a supernova is like looking back in time?

ANSWER:
Because they are far away and when we witness the event, the light has been traveling for thousands or millions or billions of years to get to us.

QUESTION:
is the energy carried by an infrared photon greater or smaller than the energy carried by a visible photon light?

ANSWER:
The energy is proportional to the frequency. Infrared has a lower frequency than visible light, so the infrared photon has a lower energy.

QUESTION:
why do bats and owls have good night vision compare to humans?

ANSWER:
You have probably heard the phrase "blind as a bat"; well, bats are not really blind but their eyesight is not very good. The way they "see" using sound waves like radar: they emit ultrasound which then bounces off things in their environment and they are able to navigate by hearing the echos. They might as well be blind. Owls, however, have very good night eyesight. There are several things about their eyes which give them good night vision:

Their eyes are quite large,
the iris can open very far to let in more light,
the eye is cylincrical rather than spherical which allows the retina to be larger,
the retina is packed with a great many "rods", cells most sensitive to low-level light (cones, the other type of vision cell, allow color vision), and
the back of the retina is reflective which means that light which does not interact with the rods on its way in gets another chance.

Most animals have better night vision than we do because of the reflective layer called the tapetum lucidum which we do not have. That is the reason that the eyes of many animals at night tend to shine when light is shined at them--it is reflected back.

QUESTION:
Why does the fundamental wavelength of a string increase as the tension on the string increases?

ANSWER:
You are putting the question wrong since "fundamental wavelength of a string" really has no meaning. The fundamental frequency of vibration of a string clamped at both ends depends on the length of the string and the speed of waves in the string. For the fundamental, the wavelength on the string is 1/2 of a wave and the velocity is proportional to the square root of the tension. The wavelength l on the string stays the same as tension increases but velocity v increases. The frequency with which the string vibrates is given by f=v/l, so the frequency increases when the tension increases (which is, of course, the way you tune a stringed instrument). If you are asking about the wavelength of the resulting sound (which has frequency f) then it is given by l_s=v_s/f where v_s is the speed of sound in air and l_s is the wavelength of sound in air, so that wavelength is shorter when the tension is increased because the frequency is larger.

QUESTION: ;
I understand the theory behind evaporation - some molecules have average kinetic energy that is great enough to enable them to escape the intermolecular forces that hold them together as a liquid. I'm given to understand that the kinetic energy is a Maxwell distribution? A bell curve? Also, when evaporation occurs, the liquid becomes cooler, because it, as a whole, has less energy. If this is so, why does evaporation go to completion? So the majority (or large portion of molecules) dont have enough KE to escape, and when the ones that DO have enough KE to escape, actually do so, the temperature (and hence average KE) decreases for the liquid - shouldnt this mean that LESS molecules have enough energy to escape, and then evaporation will eventually stop?

ANSWER:
The Maxwell distribution is not a bell curve since it cannot exist below zero. And, this distribution of kinetic energies is for ideal gases. But neither of those points are really germaine in answering your question; the important point is that the distribution is something which has one maximum the position of which depends on the temperature, approaches zero as kinetic energy approaches infinity, and is zero at kinetic energy equals zero. So, as you state, a small but nonnegligible number have kinetic energies large enough to escape; of course the direction of the velocity matters too (velocities into the fluid will not come out even with enough energy). Now, when the high-energy particles escape they leave a gap in the distribution and so, in order to maintain the same distribution of energies some lower-energy particles speed up but, in order to conserve energy this means the whole distribution must shift to a lower temperature (that is some other paricles slow down); that is the cooling. Rate of evaporation does depend on the temperature, but this is not a huge effect for modest temperature changes. In the real world the fluid is usually in contact with its environment and tends to come to thermal equilibrium with it; hence, when you set a glass of water on the table in a room at a given temperature, water will evaporate at a pretty constant rate as the room continually warms up the water. The most important factor affecting evaporation rate is the surface area and that does not change. Finally we get to the situation where only the last single-molecule layer is left. Now the overriding factor is how does it bond (or not) to the substrate. But even if this last layer of water stayed there, you would likely judge the container as bone dry because the number of molecules, while still very large, would be tiny compared to a macroscopic amount of fluid (say a teaspoon of water).

QUESTION:
When two objects "a" and "b" make an elastic linear collision, the after ci=ollision velocity of object "b" is given by Vb'=(2Ma/(Ma+Mb))Va+((Mb-Ma)/(Ma+Mb))Vb And a similar equation holds for object "a". As I understand it, these equations are derived algebraically from conservation of kinetic energy and conservation of linear momentum. Suppose the objects are billiard balls and each is rotating about its center of mass with constant angular velocity. If I assume no energy is lost due to friction when the two surfaces are in contact (ok, maybe not realistic, but it doesn’t seem too unreasonable for an approximation ??), would analogous equations hold for angular velocities? ie, can I replace mass by moment of inertia and replace velocity by angular velocity in the above equation to get after collision angular velocity? I can’t see why not, given that angular momentum and rotational kinetic are conserved, but I have not seen such formulae anywhere.

ANSWER:
The equations you quote are true only for one dimensional collisions, collisions where all the velocities before and after are directed along a line. There is a much more general solution if the balls scatter to different directions. You are right, angular momentum must also be conserved if the balls come in with spins as long as the table is frictionless; otherwise the table would exert an external torque. Also, the angular momentum due to the velocity of the balls could not be ignored; they have no such angular momentum in a head on collision, but that would probably not be the case usually. In addition, the pertinent inertial parameters would be moment of inertia, not mass. If there were friction when the balls were in contact, angular momentum would still be conserved but energy would not, further complicating the problem. So the answer to your question is a resounding no: there is no such simple equation for the real world situation. The problem is sufficiently complicated that numerical methods on a computer would likely be required to make accurate prediction.

QUESTION:
The compressions and rarefactions of sound waves generate adiabatic temperature fluctuations in the medium (take air). Is there any limit to the temperature fluctuation? or., is it possible to create sound waves with such an intensity that TEMPERATURE inside COMPRESSION reaches SEVERAL THOUSANDS (if not possibly millions) of degrees (and temperature of rarefaction reaches NEAR ABSOLUTE ZERO)? (it is useful to completely sterilise the air)..

ANSWER:
Let's look at the pressure fluctuations in a sound wave. At the threshhold of pain, the loudest sound you can hear without feeling pain, the pressure variations amount to about 30 N/m²; compare this to the pressure of the air, about 100,000 N/m². I believe that the resulting local temperature fluctuations would be negligible.

QUESTION:
How would I draw a diagram that shows refraction of light that causes "water-like" mirages on the pavement.

ANSWER:
I plagarized this from Tipler's excellent book Physics For Scientists and Engineers, Freeman/Worth Publishers.

QUESTION:
Why does a diamond glitter so much?

ANSWER:
In a nutshell, it is because diamond has a very high index of refraction, 2.42. For reference, the indices of refraction of glass and water are about 1.5 and 1.3 respectively. What this means is that light travels much more slowly in diamond than in air and the result of this is that it is very much bent when it goes from air to diamond or vice versa. It also has the effect that much of the light which enters the diamond does not go through but is reflected back (due to something called total internal reflection, also the way that fiber optics works). This effect can be accentuated by cutting the diamond cleverly and that is the purpose of the facets. Therefore, the "glittering" is because most of the light which strikes it bounces back toward you.

QUESTION:
I am learning about magnetos in school, and we were taught that they have a tendancy to arc at high altitudes. Why is this? Does the Permittivity of air change with temperature and pressure?

ANSWER:
The only thing I found about this topic is very interesting. It says that the arcing is temperature dependent, not altitude dependent. Thus, when a pilot takes off the temperature of the coil is relatively low but, as time goes on, the temperature of the magneto gets higher and, of course, this will be happening at higher altitudes so the pilot reports that the magneto problems occur at higher altitudes but the culprit is really temperature. You can read a more complete explanation here.

QUESTION:
If the effects of general relativity are taken into account then does mass of an object A near another large massive object B depend on A's distance away from B?.

QUESTION:
Consider this situation where a heavy ball of'rest mass' of value 'm0' be thrown upwards at velocity 'v' such that it reaches the height 'h' before falling back; according to the law of conservation of mass-energy, the sum of kinetic energy,potential energy and the energy of 'rest mass' (m0c^2) are conserved at ground as well as at height h. But the gamma factor isn't same. Let m1 be the relativistic mass due to velocity at ground and m2 be the 'rest-mass' at height h. Apparently m2=m1 since the mass-energy is conserved. but m1=m0*gamma(v) at ground,hence m2 = m0*gamma(v) at 'h'. clearly the gravity was little less at 'h' than it was at the ground. Does that mean that the "rest-mass" will be more under less gravity?

ANSWER:
These two questions both essentially ask the same thing--what is rest mass in general relativity. Having done a little research, I find that this is not an easy question to answer because several different definitions are used. A discussion of this question would be too lengthy for this site, but there is a good discussion at Answers.com.

QUESTION:
A polythene rod can gain a negative charge when rubbed with a cloth. a) Explain, with reference to electrons, what has happened? b) Why is difficult to detect any charge on the cloth?

ANSWER:
This is called the triboelectric effect. In fact, for charge to be transferred from one to the other, only contact is required, not rubbing. Different materials are placed in the "triboelectric series", those near the top tend to give up electrons (become positively charged) and those near the bottom tend to gain electrons (become negatively charged). Polyethylene is near the bottom and wool or silk near the top, so the polyethylene gains electrons on contact. The magnitude of the effect depends on many different things and is generally not very predictable. You can read a detailed explanation in Wikepedia. I am not certain why the charge on the cloth is not so easy to detect, likely that it is easier for something to gain electrons from the air (lose positive charge) than to lose them (lose negative charge). Or maybe it is because the cloth has so much more surface area over which to spread the charge. Or maybe the sharp points (fibers, rough areas, etc.) in the fabric encourage corona discharge.

QUESTION:
How can you tell if a point is 180 degrees out of phase?

ANSWER:
I presume that you mean phase relative to some other wave. First, define a periodic wave: it is one which, after some elapsed time T (period) repeats exactly what the wave did since the time t=0 until time t=2T, and so on. One could also define it in terms of space: it is one which, at any particular time, repeats its shape when you travel along a distance l (wavelength). Let us call the the time of the beginning of the wave t=0 and the time of the end of that one period t=T. Then 0 corresponds to 0 degrees and T corresponds to 360 degrees. Thus, the exact middle of the wave corresponds to 180 degrees. Now, if another wave of the exact same shape is such that its beginning is at t=T/2, it is said to be 180 degrees out of phase with the other wave. An example of two waves 180 degrees out of phase (red and black) is shown at the right. Notice that if you were to add these two waves up you would get zero; that is another way you can tell if two waves are 180 degrees out of phase. You really should think of waves, not points, as having relative phase.

QUESTION:
what would be the weight of a astronaut standing on the moon whose earth weight is 180lb

ANSWER:
The acceleration due to gravity on the surface of the moon is about 1.6 m/s² and on the earth it is about 9.8 m/s², so the weight of something on the moon is (1.6/9.8)W_e where W_e is the weight on the earth.

QUESTION:
When an airplane engine spins, it creates an image of the propeller standing still or barely rotating. You can also see this with car tires, fans, or any other spinning things. What causes it to look as if the propeller is barely rotating when it is at high rpm's?? Also, why does the image change directions???

ANSWER:
I do not believe that you will see this effect in sunlight, just artificial light which has an otherwise imperceptible flicker. Also, you often see this effect in movies or on television (you know, the wagon wheels on a western which look like they are going backwards). The explanation is in an earlier question I answered.

QUESTION:
How can photons exert pressure (Nichols Radiometer) if they have zero mass?

ANSWER:
In special relativity we find that anything, like a photon, with zero mass travels with the speed of light and that it posesses both kinetic energy and linear momentum. Since a photon has momentum it can transfer momentum to something and thereby exert a force.

QUESTION:
G is the graviational constant, but I don't know what it's worth. I don't know what the mass of an electron is either, or a proton for that matter. But what, according to the best numbers we have, would be the strength of the gravitational field of a electron, proton, or heck, even a neutrino be?

ANSWER:
You can easily look these constants up. G=6.7 x 10^-11N m²/kg², m_e=9.1 x 10^-31 kg, m_p=1.7 x 10^-27 kg, F_g=Gm_pm_e/r² where r is the distance between the two. I take r=0.5 x 10^-10 m, approximately the size of an atom. The force turns out to be about 4 x 10^-47 N. To put this in perspective, the electrical force between the two is about 9 x 10^-8 N, so gravity is totally negligible on the atomic scale. The neutrino mass is far less than that of an electron, so gravity plays essentially no role in its interactions either.

QUESTION:
As I was driving down the street looking at houses on my right, I noticed my cars shadow on the houses (approching the streetlamp on my left). My shadow caught up and passed me. Like a lever and I was the fulcrum. Using this anology, if light approched an object closer that its shadow was cast, wouldn't the shadow be moving faster?

ANSWER:
Yes.

FOLLOWUP QUESTION:
You answered "yes" to my posted question about a light approching an object that cast a shadow further than the distance of the lights approach. Faster than light speed! I thought light was the theoretical limit?

ANSWER:
I guess I don't understand your question. There is no difference between your moving or the source of light moving. For example, if you move at 50 mi/hr, the source is at rest, and the shadow moves at 150 mi/hour then the shadow moves at a speed of 100 mi/hr relative to you. If you are at rest and the source moves with a speed 50 mi/hr then the shadow moves with a speed of 100 mi/hr relative to you. This assumes that the geometry has not changed (distances between you and the source and the shadow. The "speed limit" is that nothing can move faster than the speed of light, not, as you seem to suggest, faster than the source of the light. However, it is subtler than this. In fact, the shadow may move faster than the speed of light because the shadow is not "something". You more often see the example of taking, for example, a laser beam and shining it on the moon; now rotate this laser very fast so that the spot on the moon moves faster than the speed of light (which is pretty easy to do). But, that spot, again, is not "something". The acid test is that if you imagine the shadow moving (more quickly than the speed of light) from point A to point B, you must not be able to use this moving shadow to transmit information from A to B.

QUESTION:
This question deals with free-float. An object is falling toward earth. A tunnel has been previously excavated completely through the earth at exactly the location of the object's landing, through the core and out to the other side of the planet. The object continues its fall through the tunnel without touching the sides of the tunnel. I know the earth's rotation is an issue, but imagine that the object makes it through untouched. Where would the object stop its fall? Newtonian gravity was described as an attraction to the center of the planet. But that is no longer our understanding of gravity. Would the object, travelling at its terminal velocity exit the earth on the opposite side, travel up into the air, then fall back to earth? Or would the object travel just to the surface on the opposite side, then fall back into the hole, thus continually boomeranging through the earth? Or maybe something else?

ANSWER:
I recently answered this question.

QUESTION:
Have you seen ' YouTube - Walter Lewin Makes a Battery out of Cans and Water ' I have never seen anything like it !! My friend asked me to give it my best shot.. we are both in our 50's, and not students.. My response is below. Do you know how this works?

ANSWER:
This is called Kelvin's thunderstorm or Kelvin's waterdrop electrostatic generator. There is a pretty good explanation here.

QUESTION:
Which is the difference between matter and waves? Which is property that says that matter is matter and waves are waves?

ANSWER:
Everything is both particle and wave. If you look for a particle, you will find one. If you look for a wave, you will find one. The classic example is light. If you take light of a particular color (wavelength) and do an interference experiment (for example the Young double slit experiment) you will only be able to understand the experiment if you say "light is a wave". If you take the very same light and shine it on a metal and measure the properties of the ejected electrons (photoelectric effect) you will only be able to understand the experiment if you say "light is particles".

QUESTION:
If Resistance of super conductors is ZERO then how would we calculate amperes if a current is flowing through it formula:- Amps=Volts / Resistance.?

ANSWER:
Ohm's law is not universal, it only applies approximately to some materials under some conditions. There is no reason to suppose a superconductor is ohmic (obeys Ohm's law) but it does: V=IR, so if R=0, then V=0 no matter what I is. So a current may flow with no potential difference. Another way to say it is that a superconductor is everywhere at the same potential regardless of any current flowing through it.

QUESTION:
If two hydrogen atoms are sitting alone next to each other, and they then combine to form a hydrogen molecule, what happens to the energy produced by this reaction? What form is it in?

ANSWER:
This is just a chemical reaction, and, as in most exothermic reactions, the energy appears as heat. On a more microscopic scale, the energy is in the kinetic energy of the H₂molecules.

FOLLOWUP QUESTION:
My question now is what kind of motion does the hydrogen molecule acquire? When the (identical) hydrogen atoms snap together to form the molecule they are moving straight at each other; I can't picture in which direction the molecule would move away, or is it the case perhaps that the molecule wouldn't actually move away, rather the bond between the atoms would stretch and contract in an endless oscillation (endless anyway until we introduce something else into the system such as other molecules for this one to bump into)?

ANSWER:
If the two were moving in opposite directions with equal speeds, then they would have to be at rest afterwards (that is their center of mass must be at rest). So the energy would have to be in internal energy of the molecule, either rotating or vibrating. In this case, the excited molecule would either break back apart or would decay to the ground state via radiation. These "inelastic" mechanisims for conserving the total energy could happen also in cases where the two did not happen to have zero linear momentum before the collision. So, if you want to understand it completely, it is more complicated than just an increase in temperature.

QUESTION:
In a nuclear reactor, a neutron hits a uranium atom, causing an explosion, then a chain reaction. Where does the first neutron come from?

ANSWER:
A fissile material, like uranium or plutonium, will usually have a small probability for spontaneous fission, that is fissions just happen randomly in the material. Therefore you don't really need a source, your fuel will provide needed neutrons to get the chain reaction started. However, although I am not a nuclear engineer, I suspect most reactions have a separate neutron source. The best known source historically is to take an alpha particle emitter and coat it with a light nucleus like berylium and there will be a reaction with neutrons as one of the reaction products; one is the PuBe source, using plutonium and berylium. you can learn form by looking for neutron source in Wikepedia.

QUESTION:
What are the properties of the cambdien rods that absorb neutrons in a reacto to control the rate of reaction?

ANSWER:
I believe you mean cadmium. There are hundreds of stable nuclei and you can shoot a slow neutron at any nucleus and there will be a probability that the neutron will be absorbed. This probability is quantified by a quantity called the neutron absorption cross section s, the larger the probability the larger the cross section. Some cadmium isotopes have unusually large values of s.

QUESTION:
what happened after Galilio threw the two balls?

ANSWER:
It is my understanding that the experiment probably never took place, that is it is an apocryphal story. See this link. If it did take place as legend has it, the two balls of different weights would have hit the ground approximately simultaneously.

QUESTION:
How was the speed of light calculated?

ANSWER:
I believe that the first part of an earlier answer will answer your question. Essentially Maxwell's equations predict waves which travel at the right speed.

QUESTION:
One thing that has always been a question: When Rutherford fired "positive particles" at gold foil, how was he able to separate atoms in order to "shoot" these particles out? Similarly, when we talk about speeding protons around a supercollider (like the Large Hadron Collider), again, how are these protons isolated so they can be accelerated?

ANSWER:
Rutherford used alpha particles which came from radioactive decay from heavy nuclei, that is these positive particles exist charged in nature. However, one can rather easily make alpha particles from helium gas by simply removing the electrons from the nuclei. Similarly the protons for a proton accelerator can be made by ionizing hydrogen. There are many types of ion sources but the simplest to think about is simply a spark which is nothing more than a plasma of electrons and positive ions in the gas allowing current to flow (mainly the electrons) across a large voltage difference.

QUESTION:
Hi, if you change the mass of a ball rolling down an inclined plane and the angle of the slope is constant the final velocity of the ball will always be the same no matter what its mass is! I know this is because acceleration due to gravity on earth is constant but is there a better explenation. Is it because you break the weight of the ball into two vector components: Force parallel which accelerates the ball down the slope and also Force perpendicular which supplies the normal force to the ball. When the weight of the ball increases the two vector components also increase and Force parallel increases to a magnitude which accelerates the ball at the same rate if its weight were less. F=MA then if M increases F parallel will also increase and A remains constant?

ANSWER:
You are making this harder than it need be. Essentially the reason that the acceleration of gravity is constant is that weight is proportional to mass and acceleration is proportional to mass and so acceleration is independent of mass. See an earlier answer.

QUESTION:
When sleeping on an air mattress does a person's body heat become lower than if they were sleeping on a standard mattress? Is there any heat transfer?

ANSWER:
I think your question is answered by an earlier answer. If you sleep on the cold ground, for example, heat will be transferred more quickly from you to the ground by convection if you are on an air mattress than if you were on a mattress which is a poor conductor and consists of many "tiny air mattresses" as explained in the earlier answer.

QUESTION:
How is it that gravitational compression can dominate electrostatic repulsion between protons in our sun to result in temperatures sufficient to support fusion? I am anticipating ionisation of hydrogen and separation of electrons and protons - the former to outer regions and the latter to core.

ANSWER:
I do not see why you would assume that the electrons and protons would rise and sink respectively. In fact, when the temperature becomes large enough to ionize the hydrogen, you have a plasma; if this plasma did separate into positive and negative parts, then you would run into problems with the Coulomb repulsion. In the unseparated plasma, however, electrons around protons shield protons electrostatically from other protons (and vice versa).

FOLLOWUP QUESTION:
Why is it not reasonable to expect separation of electrons and protons under the gravitational force within the sun given the vast difference in masses of these two entities?

ANSWER:
The dynamic effects of gravity are independent of mass; for example, drop a bowling ball (proton) and a marble (electron) and both move exactly the same.

QUESTION:
A 50-kg box is pulled by a force at an angle of 30 to the horizontal. If the box accelerates at a rate of 3 m/s2 , and coefficient of sliding friction is 0.4, what is the magnitude of force pulling the box? Problems I am having: Imagining the box where is the rope attached? At the top right corner or the bottom right corner? I have not found a simple way to figure out which is cos and which is sin. Please help! I am studying for the MCAT.

ANSWER:
This is a problem where you are supposed to view the box as a point mass, that is, you do not worry about torques, etc; it is a simple Newton's second law, F=ma, problem. It makes no difference where the rope is attached. The force has a component horizontal which provides the acceleration, and a component vertical which "helps the table hold up the box". So the equations to be solved are: 50*3=-f+F*cos30 0=-50*9.8+N+F*sin30 where f is the frictional force which is f=0.4*N and N is the normal force. So you have three equations with three unknowns, F, N, and f.

QUESTION:
Aside from the big bang and black holes, are there other reasons to consider the unification of gravity and the other forces (i.e. quantum mechanics) a fundamental requisite for a complete theory of all that is?

ANSWER:
This is really a philosophy question rather than a physics question. It is the philosophical bent of most scientists to seek to understand nature using as few laws as possible. For example, if you found the laws governing the flight of a baseball and the flight of a basketball, you would be displeased to have separate laws for each; you would seek an overriding law to describe the flight of anything.

QUESTION:
What is the medium through which electromagnetic waves propagate? It's easy to see physical waves go through water. And I can understand sound waves traveling through air. But what is the stuff that carries electromagnetic waves?

ANSWER:
This is one of the classic questions in the history of physics and its answer resulted in one of the great revolutions in physics, the theory of special relativity. The simple fact is that, since it is electric and magnetic fields which are "waving" and these fields may exist in perfectly empty space, that electromagnetic waves may propogate through perfectly empty space. They are the one wave which requires no medium through which to travel.

QUESTION:
Is there a temperature at which fire will not burn? Lets say that it is 10 degree F below 0. I think you can create a burning fire at this temperature. But what if it is 200 or even 2000 degrees below 0. Is fire still possible? Or is there a point at which humans cannot create enough speed in the molecules to create flames? Just a curious question. We were sitting around and couldn't come up with a viable solution that we could all agree on nor could we discover the answer online. We all agree that a human probably couldn't survive at 2000 below 0 but you know.... Thanks for any advice you might have..

ANSWER:
First of all, the lowest temperature is -459 F which is absolute zero. It is tricky to just say the temperature at which you can have something burn since it obviously depends on what you are burning. For example, helium will not burn at any temperature and paper burns at 451 F (remember that book/movie Fahrenheit 451?). So a sheet of paper below 451 F will not burn. But if you get it burning by elevating the temperature at one corner, as it burns, since energy is being released, the adjacent paper will heat up and burn until it is all burned out; this is regardless of the temperature of the environment around it as long as there is oxygen available to support the burning. Oxygen liquifies at -130 F, so would not be available for burning unless the paper were immersed in it.

QUESTION:
Chad Johnson,Wide receiver of the Cincinnati Bengals football team recently raced a colt in a 100 meter race.Johnson covered the 100 meters in 11.720 seconds.How many miles per hour was Johnson racing at?

ANSWER:
His average speed was 100/11.72=8.53 m/s. This can easily be converted to mi/hr: 19.1 mi/hr. If you are interested in the details of the conversion, write back.

QUESTION:
does light have weight?

ANSWER:
It depends on what you mean by weight. If you mean the classical definition of the force which the earth exerts on something by virtue of its mass, then light does not have weight because it has no mass. However, if you mean is light affected by a gravitational field, then you could say that it has weight because it bends in a gravitational field as if it had gravitational mass; this phenomenon is explained by the general theory of relativity where a gravitational field is viewed as a warping of spacetime in the vicinity of a mass. An earlier answer may be of interest to you.

QUESTION:
What is the definition of dust and what is it's constituents?

ANSWER:
According to Wikepedia, dust is defined to be anything with a diameter less than 500 x 10^-6 m. This is half a millimeter, so it seems rather large to me. At any rate, dust can be composed of anything which exists as a solid at the conditions of the environment.

QUESTION:
Our sky appears blue because of the sun's light is scattrated by air molecules, and our sun appears yellow/red at sunset for the same reason. My question is will the sun appear white if you were viewing it from the surface of the moon?

ANSWER:
On the moon the sky is black and the sun is white.

QUESTION:
I'd like to ask how can I convert Coulombs to Newtons, Newton to Kilograms and kilograms to meters/second. For example how can I find the acceleration that can be caused by the pressure of say, one ton?

ANSWER:
You might as well ask me how to convert elephants to tigers. All your requested conversions are impossible to do because the units measure different quantities. A Coulomb is a measure of electric charge, a Newton is a measure of force, a kilogram is a measure of mass, and meters/second is a measure of speed (and a ton is a measure of a force, not pressure, in English units). The only possible answer I can give you is that in common (not scientific) parlance in countries using the metric system of units a kilogram is often used as a measure of weight; this is technically incorrect because weights should be specified as Newtons but in this context 1 kilogram is the weight of an object on the earth's surface which is actually 9.8 Newtons. Hence, one could say that 1 kilogram equals 9.8 Newtons when referring to the weight of an object.

FOLLOWUP QUESTION:
Yes converting was the wrong term. What about deriving these units? For instance, by the coulombs law two positive point charges of 1 coulomb gives an in-between repulsive force of 8.988×10^9 Newtons. How they got to that number?

ANSWER:
One additional thing: it is the force between the two charges separated by 1 m. Many laws of physics cannot be derived, they must be determined experimentally. Th way you come up with what that force is (after having appropriate operational definitions of what a Coulomb and a meter are) is to actually measure the force. Of course, you would not use 1 C charges because that is a huge amount of charge (as is evident from the huge force). Rather you would take, for example, two 1 mC charges separated by 1 cm in which case the force would be 0.8988 N because F=kq₁q₂/r² where k is 8.988 x 10⁹N m²/C².

QUESTION:
I have what I think are two fairly simple and related questions about transfer of heat when a person is sitting on cold metal bleachers. First, do people lose heat faster through 1) the contact with the bleachers, or 2) the exposure to the cold air (assuming no additional layers on either their lower or upper half)? Second, when a person is in contact with a cold surface, are pockets of air (like an air mattress) a better insulator than a more solid insulation material (like a blanket or dense foam cushion)? I am guessing that contact with cold metal draws more heat than cold air, and that air is better than solid, but I don't have the science to back it up.

ANSWER:
Heat is generally moved faster by conduction than by convection, so your derrier will get cold faster sitting on the bleachers than standing up; of course, since your body is a source of heat, it is possible that you can actually warm the seat up which then reduces the heat loss to the seat. The air is a better insulator than something solid for the same reason. You are right on both counts.

MORE:
One thing I should have added is that an insulator made up of many little "bags" of air is better than an equal volume of air (for example something like styrofoam). A convection current in a big container of air can be set up such that air flows quickly across the temperature gradient whereas that cannot happen in the many little volumes. That is why, of course, it is better to fill your walls with fiberglass insulation rather than just let it be filled with air.

QUESTION:
I was thinking about hydrogen and the fact that it is less dense than air, and water and the fact that it is denser than air... Could the gpe gained by hydrogen, and the gpe converted into kinetic energy by water be used? By that i mean, water is allowed to fall, some sort of dynamo is turned by the falling water (as in power stations) generating electricity. This electricity is used to electrolyse water, producing hydrogen (and oxygen). Hydrogen is allowed to rise, then when it reaches the top again, it is burnt, producing water again. Surely there is an excess energy here or am i missing something blindingly obvious? Surely the larger the distance travelled down by the water and up by the hyrodgen, the greater the excess energy.

ANSWER:
Here is the problem with your plan: If you drop 1 kg of water from a height of 100 m it acquires about 1000 J of kinetic energy. This is the most energy you could get out of the turbine generating electric power if it were perfectly efficient (which is of course impossible). Now, the energy required to do electrolysis on that water is about 1.3 x 10⁷ J. So you would have only enough energy available to do electrolysis on about 1/10,000 of the water which fell.

QUESTION:
My question is about the momentum light is know to carry . I was wondering , if an object falls into the sun , won't it get slowed down by light pressure so that it will posses less kinetic energy as it would without light pressure. Doesn't that mean the sun-object system is losing energy since the photons carry energy and that energy was used to slow down (remove energy) from the object and as they slow the object down the photon cease to exist (removing energy again).

ANSWER:
If the photon transfers its momentum by being absorbed (perfectly inelastic collision) then the photon disappears but its energy does not. The object would get that energy in the form of heat or maybe atomic excitations or ionizations. Energy of the system would not be lost when the photon disappeared but just transformed to some other kine of energy. You are right that the object will have a smaller acceleration toward the sun than it would without light pressure, but I suspect the difference would be trivial.

QUESTION:
Could you please answer this question to me? it has had me wondering for about 3 months now: What happens to energy carried by an electromagnetic wave when it interferes with another? If energy carried by a EM wave is like E^2, (E field intensity squared), and in phased interference of two waves, they add linearly, energy would be 4 times greater instead of two! Another way to pose the same problem, but with resulting energy null: Consider that I send a wave from point A, and in its way it sums with another one in point B, which travels in the same direction and way, so they share their path from that point forwards. Imagine that they add with 180º phase difference: they will "destroy" (cancel) each other, so from B onwards, there would be no EM field at all, right? then... where did the energy of wave A, and the energy of B go?? Or maybe waves do not carry energy at all? Energy conservation must hold.

ANSWER:
You should not think of there being energy at a particular point in space due to the presence of electromagnetic waves. Rather, there is a flow of energy through each point in space. Although there is always zero energy at a point of destructive interference, energy is flowing through that point. I do not believe there is any to do your proposed experiment--they simply cannot be aligned to share their paths exactly.

QUESTION:
I was told that with artificial gravity (based on rotating an object), that you would have to have something very large in diameter in order to provide the uniform gravity required by our bodies to avoid interfering with blood flow. Is there a set number for this and how was it determined?

ANSWER:
I am not aware of any rule. To set such a rule would require knowing about physiology and how much of a variation we could tolerate. You can make an estimate by making a reasonable guess. Suppose that we can tolerate a 1% change over the height of a man, say 2 m. Then if R is the radius of the floor, then the radius at his head is R-2 and so, v²/R=g and v²/(R-2)=1.01g. If you solve these two equations you will find R=202 m, large as you say. If our bodies could stand a larger variation, R could be smaller.

QUESTION:
Imagine two billiard balls coming at each other in a direct head-on collision. The billiard ball coming from the left is going 10 m/s, while the one from the right is going 5 m/s. They have the same mass and little deformation occurs in the collision. I say that the ball going 10 m/s stops dead (for all practical purposes) and gives its momentum to the other ball, causing it to reverse its direction of motion and move away at a speed of 5 m/s. My friend says this is counterintuitive - that the ball with the greater momentum should "win" (in his words). What's the correct answer?

ANSWER:
Usually a billiard ball problem assumes a perfectly elastic collision, so that is what I will do. The problem cannot be solved without specifying energy loss in the collision, and elastic means no loss. So, conserving both energy and momentum it is an easy problem. I find that after the collision both balls have reversed their directions; the one which came in with speed 10 m/s exits with speed 5 m/s and the one which came in with speed 5 m/s exits with speed 10 m/s. A quick outline of the solution:

the mass does not matter, so take it as 2 kg.
The momentum before the collision is p_b=2x10 + 2x(-5)=10 kg m/s
The energy before is E_b=½x2x(10)²+½x2x(-5)²=125 J
The energy after is the same as the energy before, E_a=½x2x(v₁₀)²+½x2x(v₅)²=(v₁₀)²+(v₅)²=125
The momentum after is the same as the momentum before, p_a=2v₁₀+2v₅=10
Here v₁₀ and v₅ are the velocities after the collision of the balls with initial speeds of 10 and 5 m/s respectively. Now solve these two equations for the two unknown velocities and you will get -5 and 10 m/s respectively. (You will also find a second solution, because the energy equation is quadratic, of 10 and -5 m/s which corresponds physically to a "miss".)

QUESTION:
Why does not the lightening go in a straight line?

ANSWER:
Lightning propagates by a series of small steps called leaders. Each leader shoots forward about 150 feet, then a new leader, often in a different direction, is formed carrying the electric current, etc. For the leader to be able to carry the current, the air must be ionized and the field relatively far from the cloud does not have an intense enough field to do this. However, the field at the tip of a leader is strong enough to do this. There is a pretty good discussion of the mechanisms of lightning at this link.

QUESTION:
I know that Einstein's account of gravitation involves the LOCAL interaction of masses. But Newton's universal constant of gravitation, G, is global. Do we throw out G as a consequence of the general theory of relativity?

ANSWER:
I am not sure I understand your question. Newton's universal law of gravitation is an empirical law, simply a mathematical description of experimental data. On the other hand, general relativity is a theory which explains why Newton's law is correct, because of the warping of spacetime in the vicinity of gravitational mass. Hence, you do not have to throw anything out.

QUESTION:
Is CONDUCTION of temperature --- none other than inter-molecular (or inter-atomic) transfer of heat energy through RADIATION? Or is there any other factor involved which makes CONDUCTION different from such radiation transfer.

ANSWER:
No, conduction is something different from radiation. If you heat up one end of an object, the molecules will contain a higher vibrational energy than their lower temperature neighbors and will transfer, via the forces between molecules, energy to them. Think of two masses connected by a spring and one of them is set vibrating; before long, the other will be vibrating too. A simpler way to say the same thing is that the energy is transferred by collisions.

QUESTION:
Would you answer a question for me? Since a quark of a given flavor and its antiquark tend to annihilate each other when they come together, how is it that a phi meson (made up of a strange quark and its antiquark), a psi meson (made up of a charm quark and its antiquark), and a upsilon meson (made up of a bottom quark and its antiquark) can exist in a metastable state and not immediately annihilate each other?

ANSWER:
There is no reason why a particle and its antiparticle cannot exist in a bound state. The best known example, perhaps, is positronium where an electron and a positron appear in a ground state.

QUESTION:
Do gravitational waves really take away the energy from system of rotating bodies? how long will it take for earth to crash into the sun then?

ANSWER:
First let us establish that gravitational waves have never been directly observed. However, there is indirect evidence where the energy of a particular binary star system is decreasing at the rate which would be expected if gravitational waves were being generated as predicted by general relativity. The rate of energy loss depends on the masses of the objects and, I am quite sure, the sun will run out of fuel and die long before there is any noticable change in our orbit due to gravitational radiation.

QUESTION:
I have a question about the twins paradox that's been bugging me for a while. In it, the twin in the spaceship is said to be under acceleration and therefore he ages more slowly than his twin on Earth. But if no frame of reference is privileged, couldn't one just as reasonably say that the spaceship remains motionless while the Earth undergoes acceleration away from and then back towards it? In that case, shouldn't the earthbound twin be younger when they reunite? The same question would also apply to mass change due to acceleration: why isn't it just as reasonable that the Earth (and every other object in the universe) should gain in mass instead of the spaceship?

ANSWER:
There is never any question as to who is actually doing the acceleration. When the traveling twin slows down he feels being smashed against the front of his ship. The earth-bound twin feels no such force. Also, the ship needs to burn its engines to accelerate, the earth does no such thing. However, I very much dislike the explanation that all the aging takes place during acceleration periods. See an earlier discussion of this. Regarding mass, there is no mass change associated with acceleration. However, a moving particle has increased mass and both twins would agree, as long as they are moving, that the other has larger mass.

QUESTION:
If gravity is understood in Relativity Theory as a distortions of spacetime, how is the use of gravitons as the particle of gravitational exchange reconciled with the relativistic model? Also, can we profitably model the electroweak and strong forces as distortions of spacetime?

ANSWER:
For your second question see the following question. For your first question, see my earlier answer.

QUESTION:
I'm a senior in high school. Over the past few years I have obtained a growing interest in theoretical physics. Anyway, recently I have been thinking over general relativity, Einstein's law of gravitation, and the Grand Unified Theory. One question has been bothering me. If the force of gravity can be defined as the curvature of spacetime, why can't electricity and magnetism, or any other force for that matter be considered a curvature in spacetime. I'm sure the answer is alot to explain in an email, so if you would rather direct me to paper's or books, or simply telling me that this approach has been tried before, I would be grateful.

ANSWER:
The answer is fairly simple, I believe. In the theory of general relativity, mass "warps" the spacetime around it so that it is curved. However, electric charge does not warp spacetime. Electric charge is the source of electromagnetic fields and mass is the source of gravitational fields. Also perhaps of interest to you is that there is a good quantum theory of electromagnetism but there is no satisfactory theory of quantum gravity.

QUESTION:
I have a question about supercooling. Last year, a fisherman I know was changing his lobster traps, and he checked the sandbags used to weigh down the traps. When he took it out, the bag was well below freezing, and immediatly began crystallizing the water in the air. I wonder if salt water can be supercooled, and would the ocean floor be candidate for the supercooling phenomenon?

ANSWER:
Two sequential questions, one about supercooling and one about superheating; that's supercool! When the water is very deep, the pressure is very high. If the pressure is high, that will keep the water from becoming ice because it is necessary that ice have a lower density than water, that is it must expand. So, if the pressure is high enough, water will be below the freezing point but not freeze. Now, bringing this water up to the surface where the pressure is lower will allow it to solidify.

QUESTION:
I have been researching zero kinetic energy and microwave fields so that I may find the answer to a question between my brother and I. From all the research I have gathered, I have not come up with proof that microwaves (from an actual microwave oven, of any variety) can cause energy pulses to increase and heat liquid well after the microwaves have ceased. Case in point - If liquid is heated for a specified amount of time using microwaves, and is then removed from the microwaves, can the kinetic energy cause the liquid to continue to rise in temp for any duration of time? Even after the microwaves are no longer affecting the liquid?

ANSWER:
Gee, I have no idea what you are talking about! I do not know what you mean by zero kinetic energy. However, what you may be asking about is a fairly well known phenomenon where a liquid will become superheated in a microwave oven. Superheated is when a liquid has a temperature above the boiling point but does not boil. This can be dangerous since it is easy to cause the superheated liquid to boil violently (just disturb it mechanically by putting a spoon in it, for example). Maybe this is what you are referring to when you refer to a continued rise in temperature; the temperature does not go up, it is just that the liquid boils. I suspect the temperature would actually go down to the boiling point when the boiling begins. For more information, go here.

QUESTION:
There are two observers standing on a stationary platform. A spark of light is emitted from a light source that is equal distance between them. From the frame of reference of the two observers, they will see the spark at the same time. If the platform on which the two observers is moving and the light source remains in the same spot as it was before. From the frame of reference of the two observers, which would receive the light first? Why is this the same/different from the first scenario?

ANSWER:
If there are two observers at rest with respect to each other and their is a flash of light halfway between them, they see it at the same time (regardless of how the source itself is moving, as long as it is halfway between when it flashes). So the answer to your question is that they will see the light simultaneously. However, and here is the catch, if you are standing on the ground and they are moving by you will not see them observe the light simultaneously but the guy at the back will see the flash first and then the second. Hence, you and the guys moving by do not agree on whether or not these events are simultaneous. This kind of thought experiment is one of the first hints leading to the theory of special relativity which finds that time is not a universal thing but depends on the motion of the frame you are in.

QUESTION:
Say there was a 1.0g bee and it started out traveling north at 5.0m/s ( with respect to the ground) and then as it was going along it collided head on with the windscreen of a 10000kg truck that was traveling south at 20m/s ( with respect to the ground) . The bee bounces off the window at 40.0m/s - north (with respect to the ground) after an imapact lasting 0.08s. Obviously the bee started out moving north and ended up moving south. this means it must have come to rest with respect to the ground, during the collision. Doesn't that mean the truck which it came into contact also stopped for an instant? Is that possible, a bee stopping a truck?

ANSWER:
Let us calculate the average force which the truck exerted on the bee during the collision time: F==ma=mDv/Dt where v is the velocity; this is just Newton's second law. So, F=(10^-3 kg)(40 m/s-(-5 m/s))/(0.08 s)=0.56 N north. Therefore the truck experiences (by Newton's third law) the same force south. So the average acceleration the truck experiences during the collision is a=F/M=(0.56 N)/(10⁵ kg)=5.6 x 10^-4 m/s²; that means that after 0.08 s the truck's speed will be decreased by 4.5 x 10^-5 m/s. So, I think we would agree that the truck's speed will never be zero. I think your confusion comes from the reasonable but untrue assumption that the bee and truck are at rest with respect to each other during the whole time the collision is happening; they will only be at rest relative to each other at one instant and that will not be the instant when the bee is at rest but rather when the bee is moving with the same (northward) velocity as the truck has.

QUESTION:
If I were to take an extended trip at close to the speed of light, and my friend were watching me, he'd observe me staying young as he grew old, due to time dilation. I would see him staying young as I grew old. So here we have two conflicting realities. How can both of these things be true?

ANSWER:
This is the well-lnown twin paradox although it is not a paradox at all since it is fairly easy to show that the earth-bound twin grows older. I have answered this question before; click here.

QUESTION:
Fill a large pot with water. Mark the water level. Remove a fourth of the water and freeze it. Place the ice chunk back into the pot. Because of the lower density of ice, a portion of the ice chunk is above the water level. Even so, is not the water level back to the original marked water level? In addition, does not the water level remain the same as the ice melts? The Arctic is a floating iceberg, while Antarctica is a landmass. Presently, areas of the Arctic are losing mass, while Antactica is gaining. Global warming enthusiasts warn that the melting of ice in the Arctic will cause the oceans to rise by various amounts. If the above is true, the cubic miles of ice at the Arctic are already reflected in present ocean levels.

ANSWER:
You are correct that if all floating ice melts it will have no effect on the ocean level. However, it is my understanding that there is plenty of ice on land to cause a problem should it melt (glaciers in Greenland, Canada, Antarctica, Siberia, etc.). I was unaware that mass of Antarctica was increasing; what is your source for this?

QUESTION:
Suppose a beam of light is travelign perfectly back and forth between two mirrors, hitting the same point on each mirror each time. Suppose these mirrors were to come closer to each still maintaining the perfect back and forth beam. Finally suppose these mirrors were to phase together. What would happen tot he beam of light? during thsi process and after the process?

ANSWER:
There are real world problems with your question. First, there is no mirror sufficiently reflective so that your experiment can be done (see an earlier answer). If there was a photon between two idealized mirrors, bouncing back and forth, when the spacing started being comparable to the wavelength of the light you would find that only at some spacings could you put in a photon at all. These are integral multiples of half the wavelength of the light.

QUESTION:
Two protons are moving side by side (parallel). Is there a magnetic interaction or just an electrical interaction?

ANSWER:
Sorry to be so long getting back to you, but I had to go back and review some relativity. There is a magnetic interaction. Imagine you are in the rest frame of one of the protons. Then it sees only an electric field from the other (which is also at rest); choose a coordinate system such that the field it sees is E=zE where z is the unit vector in the z direction. So the force it feels is in the +z direction and of magnitude eE. Now, view this from a frame moving with speed v in the +x direction. Because of the way that the electric and magnetic fields transform (I don't think you want me to go into details) there is now both an electric and magnetic field at the proton we are watching: E'=gEz and B'=(gv/c²)Ey where g=(1-v²/c²)^-1/2, c is the speed of light, and y is the unit vector in the y direction. Now, in this frame the proton we are watching has a velocity v=-xv where x is the unit vector in the x direction. The force now is F'=eE'+e(v x B')=eE. (I will leave it to you to verify that last step!) So, the force is exactly the same, but it is composed of both magnetic and electric parts if the protons are moving in our frame.

QUESTION:
When light is "slowed down" because it enters a different medium what exactly is happening? How is lights velocity rduced throught water or glass? Why does this refraction happen?

ANSWER:
The answer is a little lengthy, so bear with me. There are two important constants in electromagnetism (EM) which essentially specify how strong the electric and magnetic forces are in a vacuum; these are e₀ (electric constant, called the permitivity of free space) and m₀ (magnetic constant, called the permeability of free space). It turns out that when you do the mathematics you find that the EM equations (called Maxwell's equations) predict waves which have a speed of [e₀m₀]^-1/2 and this speed just happens to be the speed of light in a vacuum. However, things are different in a material: because the material is composed of many charges and the charges are moving, the whole medium is affected if exposed to electric or magnetic fields. For example, an electric field will polarize the molecules and this polarization will result in a weaker electric field than if the material were not there. Hence the strength of the forces are different so we need to measure new values of permitivity (e) and permeability (m) both of which are larger than the free space values. So now Maxwell's equations predict a new (smaller) velocity [em]^-1/2. In a nutshell, the speed changes because of the interactions of the electric and magnetic fields of the light with the electric charges and currents inside the material.

QUESTION:
I am revising some poorly-written curriculum materials for my Integrated Technology class, and have stumbled upon this paragraph: "Energy can not be seen since, unlike matter, it has no mass. However, it can be measured, sensed, or otherwise detected. For example, we cannot actually see the energy of a light bulb traveling through air, but we can see its illumination reflected from this laboratory manual or the walls of this room." While there is some correct information here, the statement that energy can't be seen strikes me as wrong. It seems to me the issues are: 1) We can only see energy in the visible portion of the spectrum and 2) it must be directed toward our eye for us to see it. The fact that light is not matter doesn't, in fact, matter. In fact, I would say that we can't see matter without (visible light) energy. Is my assessment correct (the explanation, as written, is wrong or at least misleading), or can you illuminate me on this subject?

ANSWER:
It is most unsettling to a physicist to read garbage like this! Energy is, simply stated, the ability to do work. It comes in all forms, not just electromagnetic (light). A moving car has energy due to its motion (kinetic). A falling skydiver has energy by virtue of his altitude (potential). A cup of hot soup has energy by virtue of its temperature (heat). A bottle of gasoline has chemical energy stored which can, as you know, be exploited. To speak about "seeing" energy is ludicrous; can you see a moving car, a falling skydiver, a cup of soup, a beam of light? It is also inaccurate to say that energy does not have mass; as we know from the theory of relativity, mass is energy--you know, E=mc²!

QUESTION:
Is quantum physics and quantum mechanics the same? If so, what is their similarities? If not, what's the difference? What are they classified under?

ANSWER:
Quantum physics usually means the early insights and advances in the study of the quantum theory. It would include Planck's explanation of black body radiation, Einstein's explanation of the photoelectric effect, the Bohr model of the atom, Rutherford scattering, DeBroglie's hypothesis, etc. Quantum mechanics is much more complete and less phenomenological and involves considerably more mathematics. There is, however, no formal definition of what each term covers and they may be interchanged more or less as you like.

QUESTION:
A sky-diver is falling toward earth. A tunnel has been previously excavated completly through the earth at exactly the location of the skydiver's landing. He continues his dive through the tunnel without touching the sides of the tunnel. I believe that Newton would have had him stop at the earth's core. Where would Einstein have him stop?

ANSWER:
First, since this is clearly an idealized problem, let us neglect air friction (which is, of course, not negligible because the skydiver has a terminal speed before he hits the ground). Until he enters the tunnel he is accelerating with a constant acceleration down. When he enters the tunnel, he experiences less and less force as he goes deeper because there is less and less of the earth pulling on him (all of the earth outside him exerts no force) until finally at the center he has zero force on him but he has his highest velocity of the whole trip since he has been speeding up the whole time. Now as he moves away from the center he slows down. When he reemerges at the other end of the tunnel he has exactly the same speed as he had when he entered it. He continues until he reaches the altitude from which he originally jumped at which point he turns around and begins the process all over again. Newton an Einstein would both agree on this. If air friction were included, he would not go as far and if he happened to stop at the center of the earth, he would stay there forever. If the air friction were included the general solution to the problem would be that he would oscillate back and forth going less far each time until he finally stopped in the center. There is an interesting aspect of this problem: when the skydiver is inside the tunnel, he moves exactly like he were a mass on an ideal spring.

QUESTION:
I was driving in my car today and thought of my physics class I took a few years ago, and tried to test my mental capability of remembering some simple concepts. I was wondering if the acceleration of my car is constant relative to a second car, is the acceleration also constant when comparing to a third car ? Then I was wondering if the velocity of my car can reverse direction when its acceleration is constant. And finally, is it true that my car with a constant speed can not accelerate?

ANSWER:
If you mean that the second and third cars are moving with constant velocities, then, yes your acceleration as measured by any other car is the same. This is the keystone of Galilean relativity and Newtonian physics since it means that Newton's second law, F=ma, is "invariant", that is all observers will agree on what the force is on an object. Yes, velocity can reverse when acceleration is constant. The classic example, of course is a projectile; if you throw a ball straight up its acceleration, when it leaves your hand, is a constant 9.8 m/s² down at all times and it clearly reverses its direction at the top of the trajectory. Acceleration is defined at the rate of change of velocity. Velocity is a vector whereas speed is a scalar, the magnitude of the velocity. Hence it is quite possible for you to accelerate if you move with constant speed; for example, if you are moving on a circular racetrack with a speed of 60 mi/hr you are constantly accelerating because the direction of your velocity is changing.

QUESTION:
Is it possible to use hollowed out asteroid, and spin it to produce artificial gravity? While I read from one of the answers that a spacecraft can only be a certain size/mass, now I am wondering whether the same size, mass limit also has effects for hollowed out asteroid, or since it has an extremely thick shell, the size/mass limit is a lot greater?

ANSWER:
Anything which has the right angular velocity can simulate gravity if you are inside it. For it to be a good approximation, the size must be large compared to you so that your head does not have a significantly different acceleration from your feet.

QUESTION:
How fast would somthing have to travel to creat a sonic boom, so strong it could break glass? ( I seen it in a movie and it seems like it should have been moving alot faster)

ANSWER:
For there to be a sonic boom the source must move faster than the speed of sound. Once there, a further increase in speed has little effect on the strength of the boom. This is more determined by the size and geometry of the source (a bigger airplane has a stronger boom than a smaller one) and by its distance from the observer.

QUESTION:
I have a calculator that converts "lb to kg" and vice-versa. If F=ma and in the SI system my force in newtons would be my mass in kilograms times my accleration (m/s/s). In english units my force would in lbs would be my mass in slugs??? times my accleration in ft/s/s. How can the calcualtor use kg (a mass) to convert it to a (force) lbs? I also use a scale that has a button that that allows you to switch between kg and lbs when "weighing or massing" things. I "weigh" about 220 lbs therefore should my mass be (220/32) 6.9 slugs which would be the same as (in SI units) 99.7 kg's-but my weight in SI units is 2156 newtons. How is they are using force and mass interchangeably? (I have been out of school a while and used slugs but was also taught there are lbs-mass and lbs-force.)

ANSWER:
Pounds and kilograms are conventionally used both as a force or a mass which is really too bad. Physicists do not do that. However, one often talks about 5 kg of onions, for example and converts that to pounds. To be really precise, some people refer to the pound-mass and pound-force; a pound mass is the mass of an object which weighs one pound-force. When a kilogram is converted into pounds it means pound-mass. It is all very confusing and should not be worried about too much. The problem arises mostly because the SI system has mass, length, and time as the fundamental quantities and the English system has force, length, and time. A slug is that mass which experiences an acceleration of 1 ft/s² if a force of 1 pound-force is applied; almost nobody uses the slug except maybe some engineers.

QUESTION:
What is it about the oblong holes in a wiffle ball that makes it curve so easily? There's a lot of information about curveballs in baseball but not so much about the physics of a wiffleball. I was just wondering if wiffeballs, which are hollow and have holes, curve for a different reason than baseballs, which are solid and have seams.

ANSWER:
Anything which moves through the air has its path determined by two things, gravity and air friction. To make an airplane lift off, you must have a higher pressure under the wing than you do on top of the wing. An airplane does this by the shape of the wing. A curveball operates by the same principle except its asymetry of pressure is the result of spin which causes the pressure on one side to be different from the other. With a whiffle ball the holes cause the effects of spin to be much larger (both because the holes disturb the air more than the seams do and because the weight is smaller so gravity has a smaller influence on the motion). I suspect the reasons for oblong holes is that you can get different effects by spinning it about different axes.

QUESTION:
Assume a batter who is 5'8" tall and weighs 120 pounds is coming up to the plate with a wooden bat, 26-28 ounces. Against an 80mph fastball thrown from the major league distance of 60'6", and assuming the ball makes contact with an acceptable point of the bat (somewhere near the sweet spot), how fast does the batter have to swing the bat in order to hit the ball: 100 feet, 200 feet, 300 feet, and 400 feet.

ANSWER:
This is a typical example of expecting elementary physics to be able to give a simple formula for everything. The fact is that elementary physics gives us the tools to start attacking real-world problems like this, but we cannot simply apply simple physics to real world situations like this. The batter does far more than just give the bat speed and these details count. The distance is also determined by the direction with which the ball leaves. The important thing you want to focus on is the speed with which the ball leaves the bat and that is greatly influenced by how elastic the collision is (wooden vs. aluminum bats, for example). If you had some measure of elasticity, you could easily calculate the speed of the ball after the collision using the masses of the ball and bat before the collision by simply applying momentum conservation. However, this is a very poor model for what actually happens because the bat is not simply flying along by itself. This whole question would be better addressed experimentally than mathematically.

QUESTION:
how much energy is needed to enter the earths atmosphere rather than being caught in an orbit? for example if a person with a hyperthetical suit that could withstand entry through the atmosphere jumped towards earth off a space station would they ever return to earth or forever be in orbit around the earth?

ANSWER:
Your question is not correctly framed. It is not energy to enter the orbit (whatever that means) which you should think of. Rather, it is just a matter of knowing how the person "jumped toward the earth". What determines what the orbit of anything will be is simply its velocity (magnitude and direction) at some particular point. So, if you just edged off the space station you would orbit along with it since both satellites (you and the space station) had identical velocities. If you push off really hard straight toward the earth, however, you would exit with a different orbit and if this orbit at some point intersects appreciable atmosphere, you would reenter. What determines whether or not this happens is basically how hard you push off.

QUESTION:
If you have a light source going from piont A to piont B, and the didtance is 50 million light years, (or whatever) and the source completely die's, you now have a light beam traveling to point B, (earth) and at the same time an asteroid breaks the beam by traveling by it, you now have a light beam that has been broken, does the beam still go, but now in two parts? Once the beam leaves point A, do you now have a light beam all on its own?

ANSWER:
Let us suppose that the source has been on for 1000 years when it goes out. You now have a beam of light 1000 light years traveling through space with the speed of light. If something crosses exactly in the center of the beam and absorbs the light from the beam for one year, then you have first a beam 500 light years long, then a gap of one light year, then a beam 499 light years long.

QUESTION:
Hi, i recently thought of an invention regarding the producition of electricity. I know that electricity is produced by various methods but ultimately all it takes to produce electricity is to spin a turbine. I was wondering if a turbine had north magnets on it and another turbine was facing the first and it south magnets wouldnt the magents attract and if one turbine was spinning wouldn't the other? This would yield twice the electricity even though it only requires on of the turbines to be powered. Would this work or is it unfeasible?

ANSWER:
Ah, the never ending quest for something for nothing! Why not just weld the two turbines together and attach each to a generator? It would be the same thing as your using magnets to "attach them together". The fact is that you cannot get more energy (electrical) than you put in (from hydro, or burning coal, nuclear fission, or whatever). And imperfect efficiency dictates that you get far less out than you put in. Now, suppose that you get one megawatt from the generator attached to one turbine; if you attach a second generator and demand one magawatt from that also you will have to put in twice as much energy.

QUESTION:
If a black hole is a singularity, how can black holes be different sizes?

ANSWER:
They cannot be of different geometrical sizes (because a singularity is a point), but black holes have mass and they can have different masses.

QUESTION:
You build a long train on a very big circular track and set it running at 100mph. On the roof of that train you build another track, and set a second train running at 100mph, so the second train is doing 200mph relative to the ground. Assuming infinitely strong building material, and no atmospheric drag, infinite friction between wheels and track, and that centripetal force doesn't throw the trains of the track etc etc. Keep on building up and up infinitely. What happens to the speed of trains at the very top of the infinite stack when they are all doing 100mph faster than the train underneath them? and how many trains in the stack to get to the maximum possible speed?

ANSWER:
Let's not think about this circular train since accelerations cause problems in special relativity and I think we can answer what your question is without circular tracks and, in fact, without having them on top of each other. Imagine trains on parallel trecks: train A is at rest, train B moves with speed 100 mi/hr relative to A, C moves with speed 100 mi/hr relative to B and so forth. There is no limit how many trains you can add in this way but no train may move with a speed greater (or equal to) the speed of light relative to any other. Thus, if you had 10⁵⁰ trains, the last train would not have a speed of 100x10⁵⁰ mi/hr relative to the first but would have a speed of just under the speed of light.

QUESTION:
ok this may be the holy grail of science and is mostly unkown but.. The Large Hadron Collider in CERN is as u probably know due to be turned on in november. Now i just have 2 questions one being a concern of mine. Firstly if they do find the higgs mechanism to be true or if they do find an equation for everything then what will its uses be other than tick a box of accomplishments. Like could this mean we could potentialy build new life, exploit matter and time...? and secondly I assume that wen they turn this on they will gradually add energy rather than full blast and potentially rip apart the universe? because I would hope if they see its too much energy as they turn it up they would stop and not get carried away by ultimate glory. But im sure 2000 scientists together have figured that out.

ANSWER:
The goal is purely intellectual, that is knowledge for its own sake which, in my opinion, is one of the defining characterstics of humankind. But, most knowledge eventually will lead to applications someday; who would have guessed 200 years ago that electricity would have ever been more than a curiosity? that someday horses would be purely for recreation? Regarding your second question, it is likely that the energy will be gradually ramped up as they start using the collider because that is the best way to troubleshoot a new accelerator. It is absolutely not because anybody thinks this could "rip apart the universe" the energy is called high energy because the particles go very fast (just less than the speed of light) so, given their size, they have very high energy. But in an absolute sense, the amount of energy any particle has is really tiny, not nearly enough, for example, to warm your cup of coffee.

QUESTION:
I THINK I understand that, in the "twins paradox" experiment, that the space traveler ages more slowly only during the period of acceleration; once she reaches the experimental speed (whether its 60%c or 80%c), then - as long as she's travelling in a straight line at a constant speed, she ages the same as her twin on earth. Is this correct?

ANSWER:
Most elementary modern physics textbooks explain the twin paradox as all the aging taking place during the noninertial (accelerating) phase of the trip. I consider this to be totally incorrect and a complete copout! One need introduce no general relativity to understand the twin paradox, the period of acceleration can be made infinetesmally short. I have previously outlined how to think about the twin paradox and you should read that; note that there is a big difference between how fast clocks run and how fast they appear to run to other observers.

QUESTION:
I recently read that all matter within a black hole gets compressed to a singularity where matter no longer exists. How can you have mass without matter?

ANSWER:
I think that what is meant here is that the mass is not in the form which we normally associate with matter, e.g. solid, liquid, gas... But mass has a much more specific definition. There are two kinds of mass but they turn out to be the same (which is explained in the theory of general relativity). One is gravitational mass: it creates and feels gravitational fields and a black hole certainly fulfils this criterion. The other is inertial mass: it causes an objece to resist acceleration if a force is applied to it, also certainly a property of black holes.

QUESTION:
Hello, I just wanted to know if there are any gases that exist that are very good electrical conductors, but do not respond to magnetism. Plasmas conduct electricity, are there any types of plasma that do not respond to even strong magnetic fields?

ANSWER:
Any moving electric charge experiences a magnetic force when in a magnetic field and any unionized gas is, in itself, a poor conductor. Therefore, the answer to your question is no.

QUESTION:
the air contains approximately 0.03% of carbon dioxide and this amount is almost constant.why is this so?

ANSWER:
Why is it almost constant or why is it 0.03%? Much of the reason that CO₂ is fairly low is that plants absorb it from the atmosphere and give off oxygen. Therefore, the northern hemisphere has a slightly higher amount than the southern hemisphere because the amount of landmass is greater in the north. Also, the level fluctuates seasonally because of the winter dormancy of many green plants. Recently, as you probably know, the levels have been steadily increasing because of people and their cars, factories, power plants, etc.

QUESTION:
I read about Cerenkov radiation and the "blue glow" that it causes. Is this glow always blue? If not, does it depend on what the medium is (water, oil, etc.) or what the particle traveling faster than light is?

ANSWER:
The intensity of the radiation is proportional to the frequency. Therefore, the higher the frequency (shorter the wavelength) the more intense the radiation (the spectrum is continuous, not of a single wavelength). Therefore, it turns out that most of the "light" is in the ultraviolet spectrum. You would therefore think that Cerenkov radiation should look purple, but the eye is more sensitive to blue so that is what we perceive. For the same reason (sensitivity of the eye) the sky is blue and not purple.

QUESTION:
How can i plot the function Sin[n pi/2]/(n pi/2)

ANSWER:
This is just basically the function sin(x)/x. All you need to do is take your calculator and, for several values of x, calculate sin(x), divide it by x, and plot. You can make your correspondence to n by n=2x/p. The only problem point is at x=0; here you have to find the limit as x approaches zero. It may be shown that sin(x)/x=1 for x=0. The curve looks like the figure to the right.

QUESTION:
Could microwaves, 95GHz 3mm wavelength, be focussed on a tiny point using lens or mirrors ?

ANSWER:
Yes, any electromagnetic wave is susceptible to focusing using reflection or refraction provided that you design your mirrors and lenses to work with the wavelength you are working with. You cannot use the same lenses and mirrors that you would use for visible light.

QUESTION:
Let m0 be the rest mass of a photon. Since it moves with the velocity of light, its energy is, E= m0 c2----------(1) This means that m0 = E/ c2 ---------(2) By Einstein’s Theory of relativity, m0 = 0 Hence, from (2) E/ c2 =0, Or, c=1/0 How is this possible?

ANSWER:
Your basic premise, the expression for energy, is wrong. The energy is given by E=(p²c²+m₀²c⁴)^1/2 where p is the momentum. Since the rest mass of a photon is zero, E=pc which tells you the relationship between energy and momentum for a massless particle. The energy of the photon is also given by E=hf where h is Planck's constant and f is the frequency of the corresponding electromagnetic wave.

QUESTION:
I'm an editor for Scuba Diving magazine, and I wanted to check something that one of our writers included in an article about how to save air when scuba diving. One of his tips is "Swim Slowly," and here is his explanation of why you should do so ...
"Water is dense and, unlike air, not compressible. To swim through it, you have to force aside your body¹s volume and (assuming you¹re neutrally buoyant) your weight in water every time you move forward the length of your body. (Imagine if you had to shove aside a 200-pound sack of sand to walk six feet.) Obviously, the faster you swim, the more body-weights of water you have to move aside in a minute, and the more energy and air you consume to do it. The energy cost of speed is even more than you might think because it¹s an exponential function proportional to the square of the speed. So swimming twice as fast requires four times as much energy and air. But the reverse is true, too: Swim half as fast as you do now, and you¹ll use only one-fourth as much air."

ANSWER:
As we all know, it certainly requires more effort to swim through water than to "swim" through air. However, this has little to do with the compressibility of the fluids and it is also not accurate to say that you are pushing the water out of the way. The reason is almost entirely due to frictional type forces and these turn out to be determined by the viscosity of the fluid (it would be harder yet to swim through honey, but its density is close to that of water). It also depends on velocity and geometry. The author is correct that the force which the water exerts on you depends on the velocity; for some velocities, fluids, and geometrical situations, this dependence is approximately proportional to the speed squared as the author states. Now, to swim through water with a constant speed requires energy; the amount of energy is the force you must exert (equal and opposite to the force the fluid exerts on you) times the distance you swim. Assuming that the amount of air you consume is proportional to the work you do, then yes it does require less air to swim some distance slowly.

QUESTION:
which is hotter and which is colder in water- black or white construction paper, and why?

ANSWER:
You have not given enough information for your question to be answered. If you have a completely isolated system in thermal equilibrium, everything will be the same temperature. If you have two objects, one black and one white, in a very large amount of water (so that its temperature is constant) being illuminated by light, the black will absorb more of the light and the energy of this light shows up as an increased temperature. The white will also absorb light but not as much so it will not get as much hotter (like something black in the sun gets hotter than something white). The water will be more efficient at carrying off this heat and so the temperature difference will not be as large as in air.

QUESTION:
I'm curious about the wavelength and frequency of light and if either relates to its speed, and if so, how? If I were to setup a laser motion detector (such as ones often used in small mini-marts to ring an electronic bell when a customer enters or leaves) and it were to operate using infared (800nm to 1m wavelength) versus if I used ultraviolet (<248nm?) and I was able to find something that moved incredibly fast in an attempt to move through the beam of light without triggering the bell which would I have a better chance with?

ANSWER:
There is a very simple relationship among speed (v), frequency (f), and wavelength (l) of a wave: v=fl. Furthermore, the speed of electromagnetic radiation, be it visible light, infrared, ultraviolet, is a universal constant (actually, it is speed of waves in a vacuum which is constant for all waves but air is virtually indistinguishable from a vacuum as far as light goes). So all light should perform the same as far as timing is concerned. However, there will be some dependence on the wavelength depending on what you are detecting; a person would absorb or reflect visible light far better than radio waves, for example.

QUESTION:
if their is a truck full of birds and the birds are sitting at the bottom of a trailer ,does it weigh the same as if all the birds are flying?

ANSWER:
There is more than one answer to this question. Let us assume that the birds are hovering or moving with constant velocities. In that case, each bird stays in flight because the air exerts a force up on him equal to the bird's weight; but Newton's third law requires that the bird therefore exerts an equal downward force on the air. Therefore the net weight of the whole truck is unchanged. All forces internal to a system cancel out in the calculation of the net force on that system because of Newton's third law. Another possibility would be if the birds have an acceleration with a vertical component; the simplest example is that all the birds are in freefall inside (probably not what you had in mind by "flying") in which case the birds would not contribute to the weight (neglecting any air friction or buoyancy). A similar question was answered earlier which might interest you.

QUESTION:
my 10 yr old son aked me the following question over the weekend and I have no idea if the answer can ever be known - but here goes:- If the universe started with a big bang and has been expanding ever since - then in the second before the big bang - where did all the matter come from?

ANSWER:
I believe that it is not understood where the energy of the universe came from.

QUESTION:
I'm a martial artist debating an old concept in martial arts that I find to be dubious in terms of the physics. Suppose I punch a heavy bag that is initially at rest. Prior to hitting the bag I have generated some momentum. At impact, my arm and body will be decelerated by the reaction force from the bag. The theory is that if I keep my rear foot flat on the ground and have a solid body connection from that foot to the punching hand, the ground now "supports" my punch and it will therefore have more effect on the target. This is often called "hitting with the ground". My suspicion is that this explanation is not quite correct. Among the confusion is that I'm not a passive object, I can continue to apply some force during impact by continuing to drive off the back foot, but I suspect this results in more of an added "push" due to the extended time interval of contact, and what I really want is the biggest impulse. I need the help of a real physicist. Does "grounding" the reaction force of a punch through my body to the ground give the punch more power, or does it just matter how much momentum I can generate prior to impact?

ANSWER:
In introductory physics courses we usually talk about momentum in terms of collisions of point masses. Here, since the various parts of your body move with different speeds, this is not quite true. But, let's think in terms of a perfect point mass M being your whole body moving toward the target with some effective speed V so that you have a momentum MV. Now, for simplicity, assume a perfectly inelastic collision and assume the target has the same mass as you do (which seems reasonable since martial arts are for fighting other folks). Then momentum conservation has MV=2MV' where V' is the speed of the two of you immediately after the collision. Hence, V'=V/2. The force which your opponent (and you) feels is the time rate of change of his momentum, that is approximately MV/(2T) where T is the time the collision lasted, so one way to increase the force is to minimize the duration of the punch. So, now let's get to your question. If you keep a foot in contact with the floor what you are doing is increasing your effective mass (the whole earth now becomes part of the system). This increases the momentum which will, in turn, increase the force applied (if T stays the same). This is a very simplistic overview but gives you the flavor of what is going on.

QUESTION:
Taking the light as a guiding agent (its invariant speed) in several thought experiments,the lorentz transformation of coordinates can possibly be completely derived,and time dilation, lenght contraction,non synchronisation of simultaneous events,and such things can be understood therefrom.But mass increase seems to be detached from this continuity of explanations. The explanation of "Mass" gets carried away by referring to Sir J.J thompsons electron experiments. Hence the question arises- Is it possible to deduce the effect of mass increase ("Mass increases by gamma factor as velocity increases"{where gamma=(1-(v/c)²)^-0.5}by purely referring to lorentz transformations?without referring to explanations and definitions from electromagnetism. The relativistic addition of velocities seems to provide some clue. Also an explanation as to how the time part of four momentum can be treated as energy is needed.

ANSWER:
All the quantities which you can derive from the Lorentz transformation are what we call kinematic quantities. Mass, force, and more importantly linear momentum and energy are what we call dynamic properties. So, just like in an introductory physics course where, after we learn how to describe motion (kinematics), we next want to understand how motion can be changed; in classical physics this leads us to Newton's laws. What happens in relativistic physics is that we quickly find that Newton's second law, in the form F=ma is no longer a true law of physics; that is, if two observers both measure the acceleration of a mass m they will get different answers for a, so that would mean that force is no longer a useful concept in that context. So what we do is look for the relativistic equivalent of Newton's laws. To do this, write Newton's second law as F=dp/dt where p=mu is the linear momentum and u is the velocity of the particle, so for an isolated system we expect to find dp/dt=0, that is the momentum is conserved. If mu is the definition of momentum, where m is what classical physicists call the inertial mass, we find that momentum conservation is no longer a true thing for isolated systems. So, what we do is to redefine what we mean by momentum such that momentum is conserved and the new definition becomes the old definition for small speeds. If we define momentum as p=gmu we find that momentum is conserved in an isolated system and p≈mu for small u. So, you see, the gamma factor comes from redefinition of momentum, not redefinition of mass. Almost all introductory physics texts say that it is mass which increases, and this is certainly a possible interperatation of the new definition of momentum. I prefer to say that m is the inertial mass of an object at rest and that p=gmu. Your question about energy being the fourth component of four momentum is too involved for this site.

QUESTION:
Is ball lightning real or hype ? If real, how is it formed ?

ANSWER:
It is real. How it is formed is, I had thought, not very well understood. However, I did find a news story from 2002 which says the mystery is solved.

QUESTION:
I'm a fifth grade teacher. A text for my students about butterflies says that the morpho butterfly, which has a blue appearance, actually isn't blue. Rather, when light is reflected off the edges of its scales, the wings appear blue. I have heard this line of reasoning with children before, from a park ranger, explaining to my students that a bluejay isn't blue either; rather, it's the light reflecting off the wings that makes it appear blue. My understanding of color is that this very reflection of light IS color, and that you may as well say that nothing really has any color, but rather, objects have properties that allow us to perceive color once light hits them. Who's naive here, me, or the book and the park ranger?

ANSWER:
Anything has color by virtue of the wavelength of light which comes from it. Our eyes can detect the color of the light and it is that which defines something's color. Perhaps we should be careful in our definition of the color of something: it is the color which we see when the object is illuminated with white light (which, as I am sure you know, is a mixture of all visible colors). I do this so we do not have to confuse the discussion with, for example, a white object which is illuminated by green light and therefore is green; let's just say it's white. So, what determines what wavelength (color) of light comes from something which is illuminated with white light? The most common mechanism is that the object absorbs light of some wavelengths but not so much others. So, if my wall has a paint which absorbs much of the light which is not red but doesn't absorb red very well, then my wall is red. But there is another very important way which nature has found (many butterflies, birds like peacocks and hummingbirds with iridescent appearances, etc.), and it is called interference. Have you ever noticed the pretty colors on a thin film of oil floating on water (like a parking lot after a rainfall), or on a soap bubble? What is happening here is that light reflects from both the front and back of the film and goes back to you. If those two waves happen to emerge in phase (that is the peaks and valleys of the light occur at the same time and same place) they add up to be very bright in that color but other colors will not add constructively and can even completely vanish if the peaks of one coincide with the valleys of the other. Although biologically it is more complicated than this (the interference comes from something called a diffraction grating formed by the "scales"), the general reason is still similar to thin film interference. If you want more detail, google interference butterflies or check out this link.

QUESTION:
If an asymmetrical object, say a spaceship shaped like a "7" in its dorsal perspective had an engine assembly like a booster of some type attached to that left-hand arm at its furthest point or very close to it, how much force in relation to the forward force would be needed to compensate for the drifting that would occur due to that forward momentum being produced by the engine being so far out? I ask because I am an Artist who enjoys (you guessed it, SciFi and Space travel)...I have designed an ship that is very asymmetrical, with the main drive being positioned practically on the farside of the rest of the ship being held away at a distance. So I was thinking of using a thruster assembly for a compensator, but I feel it would be better if there was some actual thought on this one.

ANSWER:
When a force is exerted on an object two things can happen: (1) there will be an acceleration of the center of mass of the object in the direction of the force. And (2) there will be an angular acceleration about the center of mass of the object and in the direction of the torque (that is the object will begin spinning about its center of mass). What you would want in a spaceship is to get the first but not the second. Yes, you could put another little "thruster" a large distance from the center of mass to have an equal and opposite torque, but that would be impractical since I presume you want the main engine to be very powerful so, unless you could put a small engine very far out, it would not have adequate torque. What you should do if you insist on this configuration is to point the main engine so that the direction of the force it exerts passes through the center of mass and would therefore exert no torque; this would probably be not terribly off what you might call "straight ahead" since the main engine is likely to have a very large mass and the center of mass would therefore be relatively close to it.

QUESTION:
I'm a med student working in the neonatal ICU. The attending and I were debating over this physics problem.... So when the babies can't eat on their own (not strong enough to suck) we put a tube in their stomachs and put the nutrition in for them. Usually the 30mL of food per feed is put into an open syringe (ie. no plug) which is connected to the thin tube going into the stomach. HE says that the speed at which the food goes in is dependand on the height of the syringe more than anything else. I said that this isnt' true (though I just discovered on Wikipedia that it would be if it were a syphon type system) and I think its more dependant on the length of the tube, the diameter and the viscosity of the fluid. However, I cant prove this mathematically. Could you help answer this question?

ANSWER:
Your friend is partly right if you are dealing with an ideal fluid like most introductory physics texts deal with. But you are the winner for real fluids. Imagine sending water through your apparatus; then, with everything about the experiment being identical, repeat it with honey. Surely your colleague would not argue that the times would be the same. Indeed, you would still have a good arguing point even with an ideal fluid: surely the fluid will leak out a large hole faster than the small hole.

QUESTION:
What seems like a very simple concept to me is something a friend of mine can't understand. Could you explain this in a way he might be able to comprehend? Car A is travelling along a road at 20m/s. Car B is 20m behind car A and doing 22m/s. Car C is travelling at 1000m/s. Car D is 20m behind car C doing 1002m/s. Will the time taken for A to catch B equal the time taken for C to catch D? I believe the answer to this question is yes.

ANSWER:
The important concept to understand here is called relative velocity. If you drive down the street at a speed of 40 mi/hr and another car comes toward you with a speed of 40 mi/hr, then you see it approach you with a speed of 80 mi/hr. Thus, if two cars start out at opposite ends of a football field each going 40 mi/hr, they will crash at the same time as if one had stayed put and the other approached going 80 mi/hr. They will not crash at the same place, and maybe this is what is confusing your friend. If the cars are traveling in the same direction, as in your examples, you subtract the speeds to get the relative speed. The directions of all the speeds can be taken care of by using vectors, but it is probably better to just use your common sense if you are trying to get a feeling for it. For example, if you are going 40 and the car in front of you is going 42, he is moving away from you with speed 2; if he is going 38, he is moving toward you with speed 2 and you will collide if you don't slow down. So what matters is the relative velocity. In the specific examples you state, if the two pairs of cars start simultaneously an equal distance apart, say 10 miles, the two chasers catch up at the same time. They will not, however, have gone the same distances before catching up as in my example above.

QUESTION:
I am a biologist who regularly uses chemiluminescence to expose x-ray film. During my distant days as a chemistry student, I was oriented to the theories that energy and light are transmitted as waves or packets. From one perspective, sound is merely a lower energy/lower frequency than light. Can you help me answer the two following questions: 1.Can one consider radioative emmisions (i.e. from 32-P) as merely waves with very very high frequency? 2. X-ray film depends on a chemical reaction for it to be exposed. This reaction requires energy from a source. Visable light, UV light, IR light, and radioisotopes all produce enough energy to expose the film. Can I cause the film to be exposed with high frequency audible sound of long duration?

ANSWER:
First, sound is not just lower frequency wave light waves because light is electromagnetic radiation which travels in a vacuum; sound is a disturbance in the air or other material media and cannot travel in a vacuum. There normally are three kinds of radiaocative emissions and one of them, gamma-radiation, is merely very energetic electromagnetic radiation. I am not very expert at x-ray film but I believe that it occurs via the photoelectric effect, that is one quantum of the x-ray is completely absorbed and causes the chemistry to occur. So presumably x-ray film is sensitive to a narrow band of frequencies of electromagnetic radiation and less energetic photons would not expose the film. Sound waves are not quantized and so cannot cause the chemistry to happen no matter how loud it is or how long you "shout at it". (Actually, sound is sometimes quantized inside crystal and the quanta are called phonons.) So if some important chemical interaction requires a threshhold amount of energy to cause it to happen, no radiation with less energy per photon will be detected and sound will not be detected either.

QUESTION:
Well this may seem dumb, but no one can answer it, no one can say why this is so? X²+Y²= the square root of Z² Why is this so? I had the hypotheses that it was related to the base number system, but the conclusion was false. X³+Y³= the three square roots of Z³ or rather Z*Z*Z But it did not work. Proposition One, the hypotenuse cannot be greater than the opposite and adjacent sides added together, neither can it be shorter than the longest line, this logical, needing no proof, Yet the space between is in question in Proposition One, X³+Y³= Z³ this does not transgress Proposition One, Nor does this X^N+Y^N= Z^N Z = the hypotheses, N equals the power of the base system number. Proposition Two, Therefore we can infer Proposition One with the equation above, which is X^N+Y^N= Z^N, to conclude this equation does not transgress Proposition One. Therefore why is space defined with the 2=N? To simplify, two products of themselves what is the root of them? Why Is this so? Proposition three, space could have been defined in another universe, as N=1.25, or N = 3.1, why in this universe N=2? Given the equation X^N+Y^N= Z^N. Are my Proposition correct, I think so, but why is it the power of 2 in a base system, and not for say the power of 3 in a base system. Why is this universal equation X²+Y²= Z² to space? any help would be nice?

ANSWER:
Well, this is not really a well-focused single question, but I will try to answer it. This is really a mathematics, not physics, question. The Pythagorean theorem is true for Euclidean geometry, that geometry in which we seem to live, the geometry which we learn in high school. There are hundreds of proofs which you can use to refresh yourself. It has nothing to do with the number system we use to count with. An example of someplace where the theorem is not true is on the surface of a sphere. Imagine two lines starting at the north pole which are 90⁰ apart and they run down to the equator and the equator then completes the triangle; Then all three sides are equal. Although you seem to think that it is not true that X³+Y³=Z³, that equation can be true; given X and Y you may find Z to satisfy the equation. For example, if X=1 and Y=2 then Z=(9)^1/3. What is particularly interesting about the Pythagorean theorem is that there are special cases where X, Y, and Z are all integers greater than zero, e.g. (3,4,5) and infinitely many others. One of the most famous of mathematics' unproved conjectures was known as Fermat's last theorem (1637) which states that there are no solutions where X, Y, and Z are positive integers greater than zero to the equation X^N+Y^N=Z^N with N>2. It was only recently (1995) that the proof was achieved by Andrew Wiles.

QUESTION:
i dont know how reliable a source this is, but i recently watched the movie "what the bleep do we know" and it talked about electrons and how they jump in and out, between places. it then mentioned that the nucleus of an atom does a similar thing, popping in and out. i'm not sure if i misunderstood. is the nucleus constant?

ANSWER:
I really don't know what you are asking. It probably refers to vacuum polarization where the presence of an electromagnetic field causes virtual electron-positron pairs to appear and disappear spontaneously. There is nothing wrong with this as long as it happens quickly enough that the uncertainty principle is not violated; that is, it is ok to violate energy conservation as long as you only do so for a very short time. Similarly, any particle/antiparticle pair could appear and disappear. Since both nuclei and electrons are electrically charged, this can happen near either of them. It does not mean that the electron or nucleus are popping in and out of existence, just the "clothing" in the vacuum around it.

QUESTION:
How likely is it that the laws of nature will change, making life in the universe impossible, say within 1000 years, 1 million years, and 1 billion years?

ANSWER:
Since there is no evidence that the laws of physics change at all, there is no chance based on what we know. It is of interest to astrophysicists to look for evidence that the fundamental constants of nature might change, but there is no firm evidence of its happening. In any case, it certainly will not happen within less than a million years.

QUESTION:
at what pressure and temperature will carbon melt instead of sublimate?

ANSWER:
See the attached phase diagram.

QUESTION:
I was wondering, is it possible for electrons and protons to annialate each other? Even though an electron is an elementary particle and a proton a baryon?

ANSWER:
No, it is not possible. If it were the universe would become empty of mass.

QUESTION:
Do Newton's Three laws relate to each other?

ANSWER:
I don't really understand what you are asking. The three of them together form the basis of the dynamics and statics of classical mechanics, and they are therefore related in that they all address the same types of problems. On the other hand if you are asking if one can be expressed in terms of another, that is if they are in some way redundant, the answer is no. Although many people write off the first law as simply a special case of the second law, that is not correct and each of the three conveys unique ideas.

QUESTION:
I'm currently in an argument with a few friends, some of which are in engineering whether gravity and the idea's surrounding it are covered as the Theory of Gravity or the Law of Gravity. I've been lead to believe that it is the Theory of Gravity and as such it is concidered a law merely because it has been around for so long. However, it is still JUST A THEORY. Now if I'm wrong I'll recant and apologise to them. So, is it the Theory of Gravity or the Law of Gravity. And do you have any links or references that I could use to either prove or disprove it either way?

ANSWER:
I would say that it depends on how you define a law and a theory. Here are my definitions: a law is a mathematical statement describing how something is whereas a theory is an explanation of why something is. Now, I assume that you are referring to Newton's universal law of gravitation, namely F=-Gm₁m₂/r². This is an empirical law that tells you the force which two objects exert on each other because of the gravitationsl attraction; it says nothing about what the origin of this force is, that is why do two objects which have mass attract each other. I would therefore say that this is not a theory of gravity, it is a law of physics. On the other hand, the theory of general relativity explains why two masses attract each other (because the presence of mass "warps" the space around it} and therefore is the operative theory of gravity. I should point out that either a law or a theory might be applicable only in special circumstances; for example, Newton's three laws of motion are applicable in everyday life but when you try to extend them to very large speeds or very small distances, they become inapplicable.

QUESTION: ;
while seeing from the ground the towards the sky, the long distant flight emits smoke and the trail of smoke behind looks like a cloud, like a rocket is going. Why is it so.

ANSWER:
The condensation trail left behind jet aircrafts are called contrails. Contrails form when hot humid air from jet exhaust mixes with environmental air of low vapor pressure and low temperature. Because of the high altitudes, contrails are composed of ice crystals and become cirrus clouds.The mixing is a result of turbulence generated by the engine exhaust. Cloud formation by a mixing process is similar to the cloud you see when you exhale and "see your breath".

QUESTION:
If I shoot a modern arrow straight up into the air with a bow that exerts 75 lbs of thrust does the arrow travel to the top of it's flight in the same amount of time that it takes to fall back to earth?

ANSWER:
A freshman physics class would say yes but that is if you neglect air friction. On the way up the arrow has two forces on it: its weight down and the air friction also down. On the way down it also has two forces on it: its weight down and the air friction up. The problem is complicated somewhat by the fact that the air friction force depends on velocity, so it is not possible, without stipulations on the initial speed and the details of the air friction to determine which will be quicker, up or down, but since the forces on them are definitely different if there is any air friction at all, the times will definitely differ.

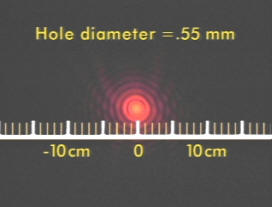
QUESTION:
What is the efect of the shape and the thickness of the slit in a single slit diffraction?

ANSWER:
By "thickness" I presume that you mean the width of the slit. This is part of the standard single slit analysis and it is found, as the slitt gets narrower the pattern expands. The shape also determines the nature of the pattern. The simplest (extreme) example would be the pattern from a hole. An example is shown at the right.

QUESTION:
My question relates to the double slit experiment. It is my understanding that when photons are "shot" one at a time through a double slit, the screen records individual dots - the pattern of which (over time) will be "striped" (i.e. consistent with a diffraction/interference pattern). Hopefully what I just said is correct? Anyway, my question is: what happens if only one single photon is shot (i.e. there is no stream of photons)...is there an inteference pattern on the screen with this one photon, or does the photon appear as a dot in the spot on the screen where one would expect it to be based solely on the particle theory? In a general sense, my question is whether the interference patterns arises from previous photons interfering with later ones rather than one particular photon intefering with itself? A related question is what happens if a stream of photons is shot but there is a "significant" time delay (not sure what time frame) between shooting each photo n...i.e. does the interference pattern disappear in this case (assuming this expt is technically feasible)?

ANSWER:
You will see a dot from a single photon. However, it will retain some of the properties of the diffraction pattern. E.g. it will not fall where the dark stripes would be for this double slit and it will not (necessarily) pass straight through like a simple particle would. It is far better to think of the photon interfering with itself rather than other photons. Indeed, the kind of experiment you refer to ("one at a time") is the same as that you allude to at the end, that is you can shoot photons through at a rate of one per hour and the diffraction pattern will still be there.

QUESTION:
if atoms can "last" for about 10³⁵ years, what happens to them? do they just cease to exist?

ANSWER:
This is not a fact but speculation. It has been proposed that protons, along with electrons the stable components of matter in the universe, will ultimately decay. Nuclei are composed of neutrons and protons and a free neutron decays to a proton, an electron, and a neutrino. The most likely proton decays ultimately end up as two photons and a positron. The positron then finds an electron and they annihilate to two more photons. Other decay modes include neutrinos also. So what happens is that when all the atoms disintegrate the universe will be filled with photons and neutrinos. I must emphasize that this has never been observed even though large, elaborate experiments have been done to try to see proton decay. The "standard model" of elementary particle physics does not predict proton decay, that is the proton is stable in that model.

QUESTION:
if a penny is placed on a rotating turntable, where on the turn table does the penny require the largest centripital force to stay in place?

ANSWER:
The centripetal force is given by mv²/R where v is the speed, m is the mass, and R is the radius of the circle in which it is moving. The speed of an object which is on a rotating rigid body (your turntable in this case) is v=Rw where w is the angular speed (in radians/s). Since w is a constant (every point on the turntable has the same rotational speed), the centripetal force is mR²w²/R=mRw². So the force increases linearly with the radius, so the answer to your question is the force is greatest on the extreme edge of the turntable.

QUESTION:
if I have the amount of momentum an object has how can I convert that to the amount of potential/kinetic energy the object has

ANSWER:
The kinetic energy is p²/(2m) where p is linear momentum and m is the mass of the object. There is no general relationship between the momentum and potential energy; however, in cases where total energy is conserved, as the kinetic energy decreases the momentum will decrease and the potential energy will increase. So, for systems where energy is conserved, you may write E=p²/(2m)+V where E is total energy and V is potential energy. You can now solve this equation for p.

QUESTION:
How do I make a guitar out of scratch? My Physics class needs to construct an instrument out of scratch and I don't know where to start. Can you help me?

ANSWER:
A guitar which demonstrates the principles should be fairly straightforward to make. Probably not too good for making music though. I would start by getting one guitar string and stretch it between two nails on a board; it would also be good if you made there be a way you could vary the tension, as the peg does in a guitar. This is a rudimentary stringed instrument. You can demonstrate that a plucked string makes sound and that the frequency (pitch) of that sound gets higher as the tension in the string gets higher (how a guitar is tuned). But the sound will be very small. That is what the box of the guitar does--it resonates and thus greatly amplifies the sound of the vibrating string. So get a box, wooden and closed on all six sides. cut a circular hole in one side and stretch your string across the hole; it would be best if the nails you strung the string between were actually in the box. It would also be good if the wood was not too heavy so that the wood itself can vibrate to contribute to the sound. I have seen this kind of thing done with a wooden cigar box.

QUESTION:
What light source will bounce/refract/reflect off of broken glass? Will regular light, a laser, or some other source. Let's assume it is clear glass

ANSWER:
Any electromagnetic radiation, and so any light, when it strikes an interface between two media (for example air and glass) will do two things: it will refracted into the material and it will be reflected from the interface. The only exception is called complete internal reflection where light inside glass, for example, strikes an interface with a material with smaller index of refraction with a grazing enough angle; it will reflect only, not leave the glass. This is how fiber optics works. But that does not seem to be your question and there will always be some light of any wavelength reflected from glass in air.l

QUESTION:
How is it possible to explain the movement of light with respect to its particle nature? that particle will reach infinite mass due to the theory of relativity.

ANSWER:
Actually, the theory of relativity predicts that any particle of zero mass must travel at the speed of light. Photons are such particle. Until recently it was thought that neutrinos were massless but we now know that they have a tiny mass. Although a graviton has never been observed, it is believed that it travels with the speed of light. A particle with a nonzero mass takes infinite energy to accelerate to the speed of light, but photons have no mass and so take no energy to accelerate to the speed of light since they are already there.

QUESTION:
what math equaion can i use to find PSI of water at diffrent hights.

ANSWER:
You want to calculate the pressure at a depth d in a large body of water. The appropriate equation is P=P_A+rgd where P_A=10⁵ N/m² is atmospheric pressure, g=9.8 m/s² is the acceleration due to gavity, and r=1000 kg/m² is the density of water. A N/m² is called a Pascal (Pa). On the other hand, you might want to compute the guage pressure which is the amount above atmospheric pressure in which case P_G=rgd; your tire pressures are measured in guage pressure. Let's calculate an example. Suppose you are 10 m down. P_G=1000x9.8x10=9.8x10⁴ N/m²=9.8x10⁴/6895=14.2 PSI. Note that I have used the conversion 1 PSI=6895 Pa.

QUESTION:
Is there any heat associated with visible light? I know heat is usually in the IR range, but is there any heat in the visible range? If so, how much and or is it measurable? For example, when using a 100 watt halogen light bulb that when turned on produces enough heat to melt wax. How much heat is IR vs Visible Light?

ANSWER:
Radiant "heat" energy usually means energy which arrives via infrared electromagnetic waves. However, there is not really a precise definition. All electromagnetic energy delivers energy to whatever it is absorbed by, determined by the intensity. The reason that IR is usually called radiant heat is of biological origin: we are mostly water and water absorbs IR radiation very efficiently. So, if IR and visible light, each with the same intensity, strike you, more of the IR is absorbed.

QUESTION:
A piece of ferromagnetic material having mass m is rolled under a permanent magnet suspended above. When it gets close enough, it's pulled up against the magnet, rising by a height h. The total work done is therefore mgh (g = acceleration due to gravity). Where did the amount of energy mgh come from?

ANSWER:
This seeming simple question is a quite difficult and subtle one. Since the explanation is too lengthy to give here, I am giving you a link here where you can study the details. Essentially, this is Faraday's law in action: when the ferromagnetic material gets magnetized it is equivalent to a current loop; when a current loop moves in an nonuniform magnetic field an electric field is induced; this electric field does the work.

QUESTION:
Assuming the speed of light is constant--light emitted from the front of a motorcycle at rest will travel at the same speed as light from a moving motorcycle. This means that if the motorcycle travels down a road with a light mounted perpendicular to the motorcycle that the light being emitted will not gain the motion of hte motorcycle, that is motion perpendicular to the motion of the direction the light is emitted will not by in anyway added to form a resultant direction and motion of the light emitted. Are the above statements correct? If not why? If yes, does this mean that the absolute motion of the earth can be found by emitting lasers tangent to its surface and measuring the difference from the expected path?

ANSWER:
As soon as you start having velocities which are not along the line of motion, it gets more complicated. If you have a component of the velocity perpendicular to the direction of motion, the velocity seen by a "stationary" will be affected by time dilation but not by length contraction. Hence, the transformation for the transverse (perpendicular) and longitudinal (parallel) components of velocity are different. If you are really interested, you can get a discussion here. The amazing thing is that the speed of light still comes out to be the same, but the direction is altered; that is, if the light is emitted perpendicular to the direction of travel, the velocity seen by a stationary observer is in a direction different from perpendicular but still of the same speed. It does "gain the motion of the motorcycle" but loses just the right transverse velocity so that the speed stays the same.

QUESTION:
What work is being done while you walk? I say the floor is doing work on you since the the floor is exerting a forward force and your direction of travel is in the same direction. Is this correct?

ANSWER:
Walking is a pretty complicated thing because it is a periodic series of accelerations and decelerations. If we look at the time averaged situation there is a constant velocity and therefore, since the kinetic energy is not changing, no work is being done. You are correct that the external force which does work in the short term, either speeding you up or slowing your down, is the frictional force between the floor and your feet.

QUESTION:
Do carbon nanotubes burn in vaccum? like in space?

ANSWER:
Nothing burns in a vacuum. Oxygen is required for burning.

COMMENT FROM A READER:
I noticed one wrong answer - a simple miswording, most likely. It was asked if carbon nanotubes would burn in a vacuum, and the answer was that nothing burns in a vacuum. This is better worded as nothing burns without oxygen, as some molecules are self-oxidizing, or can burn without a vapor atmosphere as long as an oxidizer is present.

QUESTION:
Do electrons move slower in a colder environment, like air molecules move slower in a colder environment, if not why?

ANSWER:
Yes. An important concept in physics is that of an electron gas; this provides a good model for valence electrons in a conductor since the valence electrons are essentially free to move. And the average speed of the electrons deterrmines the temperature of a gas just like in any other gas.

QUESTION:
You have a muon, which is a fundamental particle(a fermion) like an electron, whose mass lies between an electron and proton. It's lifetime is approximately 2.2 micro seconds. It then decays into a neutrino and antineutrino. My question is this. Since neutrinos have at best an extremely tiny mass, surely an antineutrino and a neutrino's combined mass does not equal the mass of the muon. So where does this extra mass go when a muon decays?

ANSWER:
For starters, you have it wrong regarding the decay. A muon is either postively or negatively charged and the neutrino or antineutrino is uncharged; therefore the decay mode you assume would violate charge conservation. The most common decay of a negative (positive) muon is m^-®e^-n_e^*n_m (m⁺®e⁺n_en_m^*) where an asterisk indicates an antineutrino. So you get one electron (positron), one neutrino, and one antineutrion. But your question is still pertinent: where did the missing mass go? There is no law that mass must be conserved (in spite of what was postulated by 18^th century chemists!) What must be conserved is total energy. Although in recent years it has been discovered that neutrinos have a small mass, it is so incredibly small that I may neglect it in this discussion. What must be conserved is energy and mass is a form of energy. Thus, assuming that the muon which decays is at rest (not necessary), the energy before the decay is Mc² where M is the mass of the muon; after the decay the energy is mc²+T where m is the electron (or positron) and T is the summed kinetic energies of the three decay products. We then equate energies before and after to conserve energy. So the missing mass shows up as kinetic energy. Since Mc²>mc², it is not possible for all the decay products to be at rest after the decay.

QUESTION: ;
If a radio signal is bounced off an object that is directly above the sending or receiving station, the signal strength is stronger at the receiver than if it bounces off an object that is midway between the two stations. I have been able to confirm this phenomenon in several books, but they all fail to explain WHY. I tried to figure it out with optics, but was unsuccessful.

ANSWER:
Since radio signals fall off roughly like 1/r² (r is how far it travels) I thought that this would be a relatively simple problem of calculating the distance of the path of each and finding that the over the transmitter path was shorter. However, choosing the height as 10 and the ground distance as 500 (units are unimportant for qualitative understanding), I found that the stronger at the receiver situation had a longer path (about 510) than the weaker at the receiver situation (about 500). So that ain't it! Next, the plane is not a perfect reflector, so maybe that has something to do with it. I now calculated, assuming a loss of half the signal upon reflection (and still 10 and 500 distances), the following two scenarios: (I will call the intensity at the transmitter I.)

For the plane directly over the receiver, the intensity it sees I/100 and the reflected intensity is I/200. Now, that signal must travel a distance of (10²+500²)^1/2, very close to 500. So the final intensity is (I/200)(1/500²)=2x10^-8I.
For the other situation, the intensity at the plane is I/(10²+250²)=1.6x10^-5I and the reflected intensity is 0.8x10^-5I . Now, the distance to the receiver is (10²+250²)^1/2, very close to 250. So the final intensity is (0.8x10^-5)(1/250²)I=1.28x10^-10I, substantially smaller.

So, I surmise, the reason is the fact that a much larger signal eminates from the plane when it is close to the transmitter.

CORRECTED ANSWER:
It has been pointed out to me that my calculations above would have arrived at exactly the same conclusion without the loss of half the signal upon reflection. In fact, that is completely right: just multiply both answers by 2 for 100% reflection and the conclusion is still the same! So, it has nothing to do with the reflectivity of the plane but rather with the strength of the signal at the time of reflection. I stand corrected!

QUESTION:
Why is there no sonic boom from light or radio transmissions?

ANSWER:
A shock wave (sonic boom in the case of sound) happens if the source of the waves is moving faster than the waves themselves. Another example of a shock wave is the wake of a boat if the boat moves faster than the water waves. Light and radio are electromagnetic waves, not their sources. If you had a light source moving faster than the speed of light, there would be a "lumen boom". However, as you probably, nothing can go faster than the speed of light in a vacuum. However, light travels more slowly in a material, for example glass or water; then if a particle travels faster than that light speed, shock waves occur. This is often seen in the water surrounding a nuclear reactor since energetic subatomic particles passing through the water are moving faster than the speed of light in water; it is seen as a blue glow.

QUESTION:
If I have two cylinders, one with an inside cross sectional area 2 square inches, and the other with an inside cross sectional area of 1 square inch; each cylinder has an airtight piston with an attached handle; each cylinder is the same length; and each cylinder has a nozzle with an inside diameter of .5 inches; which cylinder will suck up more water with the nozzle if an equal amount of force is exerted on the handle? And what are the laws of physics that would govern this situation?

ANSWER:
You need the continuity equation and Bernoulli's equation to do this. I find it easier to think about the fluid moving the other way which is equivalent, so that is how I will do it. I will use the following notations: at the the nozzle the speed of the fluid is v₂, the cross sectional area is A₂, and the pressure is P₂; at the piston the speed of the fluid is v₁, the cross sectional area is A₁, and the pressure is P₁. The pressures are P₁=P_A+F/A₁ and P₂=P_A where P_Ais atmospheric pressure and F is the force applied. The continuity equation states A₁v₁=A₂v₂; this simply says that the rate of fluid in is the same as the rate out. So, you may solve for v₂ which is not of interest to us: v₂=A₁v₁/A₂. Now, Bernoulli's equation says that P₁+rv₁²/2=P₂+rv₂²/2 where r is the density of the fluid. (This is not the most general form; if the nozzle and were at significantly different altitudes y then there would be a rgy term added to each side of the equation.) Now, if you do all the algebra you will find that v₂²=2FA₁²/[(A₁²-A₂²)r]. One important thing to note is that if A₁ is much greater than A₂ the speed out is independent of A₂: v₂@2F/r. For your cases, A₂=.5, A₁=1, and A'₁=2 (units are not important since the areas enter as ratios), then v₂²=2.67 F/r and v'₂²=2.13 F/r so the thinner piston moves fluid through the nozzle faster.

QUESTION:
If I drive slowly on my dirt road it rattles my teeth. If I drive fast it feels better. What's best for the suspension of my truck (and my teeth)? Driving fast or slow?

ANSWER:
If you have a bump and go over it you experience an acceleration and Newton's second law says there must be a force causing the acceleration. The faster you hit the leading edge of the bump the greater the acceleration, so the greater is the force you feel. This is basically how speed bumps work, However, if there is a series of small bumps relatively close together the inertial of your car might carry you from one to the other so that you do not have to go up the leading edge. Also, since your springs are relatively stiff, a high bumping frequency has the wheels bouncing but the car (and you) not moving as much whereas at a slower speed the car and wheels and you move more as one. I guess my rambling says you should go faster (as long as you can maintain control).

QUESTION:
Is it possible the reason why Electrons do not fall into the nucleus is; the closer an Electron gets to the nucleus it's charge is diminished, or it begins to become more positive and repelled? 2nd, the reason why it does not fly away from the nucleus is; the farther away it gets from the nucleus, it becomes more Negatively charged?

ANSWER:
Your suggestions are not possible. One of the most sacrosanct of all physical laws is conservation of electric charge. The charge of an electron never changes under any circumstances.

QUESTION:
I have a question that no one seems to be able to answer. If mass can be converted to energy at the speed of light, under what condition(s) can energy be converted to mass? I am trying to imagine what the inverse of the speed of light might be.

ANSWER:
I do not know what you mean by "converted to energy at the speed of light"' or "the inverse of the speed of light"; let's just say that mass may be converted into energy. I take it your question is then "under what condition(s) can energy be converted to mass?" Well, any condition you like provided that rules like charge conservation, energy (including mass energy) conservation, and momentum conservation are obeyed. Here is one example: the nucleus of an atom has a mass smaller than the sum of its parts (neutrons and protons). If you now disassemble the nucleus you will, of course, have to add energy (that is, do work) which shows up as increased mass of the system. Note that the inverse is also true, that is if you take a bunch of neutrons and protons and push them together you will get a net gain of energy by creating the final nuceus; this is how stars work.

QUESTION:
Is it possible to create elements like gold or titanium in the nuclear fission/fussion reactor? Is it likely that we would be able to create at least a few atoms of it sometime in the future?

ANSWER:
Not only is it possible, it happens all the time. By definition, a fusion or fission nuclear reaction starts with fuel and turns it into something else. In the case of fission, take uranium, for example. When it fissions, it splits into two nuclei. Those that you give as examples, gold or titanium, are unlikely (not impossible) because the distribution of fission products tends to fall mostly between rubidium and gadolinium (see Wikepedia for more detail). For fusion, we get the sum of the fusing nuclei, for example hydrogen plus hydrogen fuses to helium, helium plus carbon fuses to oxygen, etc. Inasmuch as the early universe was all hydrogen, the very existence of other elements today proves that they were created (in stars) via fusion.

QUESTION:
I am interested in determining the amount of friction (and subsequently heat) generated in primitive friction fires. I have read about calculating coefficients for static and dynamic friction, and am wondering if there is another formula that is more applicable. The fire-making method I have in mind involves the rotation of a wooden dowel (with a rounded tip, like a half-sphere) in a wooden socket with a corresponding half-spherical shape. I would like to be able to compare the amounts of friction for various wood species, and use that information to determine how much heat can be generated with a given diameter dowel. Any help would be greatly appreciated.

ANSWER:
Friction is a very tricky thing. In its simplest form, the frictional force, which will determine the heating rate, is proportional to the normal force (how hard the two are pressed together. In your case, however, the temperature varies and so the proportionality constant (coefficient of friction) will not be a constant at all but vary with the temperature. Physics is not just a theoretical science but equally an experimental science. In a situation like yours, the best way to study this problem is to do experiments.

QUESTION:
Are there places in an atom, where the electrons are located, that make it more likely that electrons will form bonds?

ANSWER:
I am not sure what you are asking. The electrons most involved in chemical properties of atoms are the valence electrons which are generally the outermost electrons.

QUESTION:
Why does light get dimmer as it gets farther away?

ANSWER:
If you have a source which is radiating in all directions, like a light bulb, then if you get a distance from it which is large compared to the size of the filament, then, as you say, the light gets dimmer as you get farther away. That is because light carries energy and that energy gets spread out over a larger and larger area as you get farther away. The intensity of light is defined as the energy crossing a square meter in a second and that gets smaller, of course, as the available energy spreads out. Not all light gets dimmer as you go away: a laser is light which does not spread out but stays in its narrow beam, so the spreading is very small so the intensity is very nearly constant as you go farther away. Laser beams have been shot to the moon, reflected back, and lose very little intensity.

QUESTION:
do have more than one point free of electrical filed in a square with 4 charges at its edges

ANSWER:
I assume you mean equal charges. Field will also be zero infinitely far away.

QUESTION:
Of what matter is moon made of ?

ANSWER:
See http://www.nasm.si.edu/exhibitions/cchoice/moonrocks/moonrocks1.htm

QUESTION:
I have heard that cold can eventually "seep" through anything, no matter what it is made of. I was wondering if this is correct.

ANSWER:
"Cold" is a qualitative concept and it is meaningless to ask if "it" can "seep". If you have two objects with different temperatures, then energy will be transferred from the higher temperature to the lower temperature until equilibrium is reached (equal temperatures); this will happen regardless of what is between them (provided that it is an isolated system) since there is no perfect insulator. The energy transfer, if there is a vacuum between them, will be accomplished via radiation.

QUESTION:
Please tell me if you know how to separate water into gasses with electricity or any other way for that matter. - I would like the most to know how to do it at home and possible safe one too, but anything is better tan none so please give me any info that you can on this topic.

ANSWER:
Check out http://www.reachoutmichigan.org/funexperiments/agesubject/lessons/energy/split_h2o.html

QUESTION:
I was watching the science channel today and was learning about the theory of dark matter. I had a fundamental issue with this idea because it simply places a unknown into an equation that satisfies the answer which we expect/is projected based upon our own understanding of physics. This idea simply seems too easy a solution. I began thinking about quantum physics of which I know little to nothing about. What I do know is that quantum physics is necessary because the laws of physics which apply to our daily life at human scale do not apply to that of subatomic particles. The show was trying to explain the reasoning behind galactic rotation. The show stated in order for galaxies to rotate at a uniform speed from their inside to their outside without the galaxy destroying itself there must be necessary unseen mass(Dark Matter). My question is why if on a small anatomic scale physics is altered making mass behave differently wouldn't it also, on a much larger scale relative to daily human life, make particles also act in a completely unique form of physics? I was wondering this because although it is a generally baseless theory the idea would make dark matter totally unnecessary.

ANSWER:
Most astronomers and astrophysicists seemingly have no problem postulating the existence of dark matter to explain many observations which seem to indicate its presence. However others, like myself, find this to be sort of akin to the postulation of the "luminiferous aether" postulated to provide a medium through which light waves could propogate. What you are suggesting is, in fact, quite reasonable: until we can test with precision that our laws of nature are the same at very large distances, it is somewhat presumptive to assume that they must be. I should warn you, however, that most mainstream astrophysicists would not be in agreement with this point of view.

QUESTION:
If the earth suddenly shrinks to half of its present radius, the acceleration due to gravity will be what?and why?

ANSWER:
Assuming that the mass remains the same, the gravitational force, and thus the acceleration due to that force, would increase by a factor of 4 because the gravitational force is inversely proportional to the square of the distance from the center.

QUESTION:
What is the temperature of fire?

ANSWER:
It depends on many things, like what is burning, what the environment is like, etc. Typical temperatures are around 1500^o C. A little more detail on different kinds of fires may be found on Wikepedia.

QUESTION:
Is it possible for a helicopter to hover above the Earth and have the Earth move under as it rotates so that the helicopter would "travel" around the Earth in 24 hours?

ANSWER:
Inasmuch as the earth drags its atmosphere with it, the helicopter would have to travel at a speed much larger than helicopters go relative to the air to remain in the same position in space as you stipulate. So, no it is not possible.

QUESTION:
What happens to the atomic number and mass number of a nucleus when it emit (a) a positron? (b) a gamma ray?

ANSWER:

charge decreases by one unit, so atomic number decreases by one; mass number stays the same.
mass number and atomic number are both unchanged

QUESTION:
I am a 9th grade student currently attending Nelson County High School in Kentucky. The other day i learned in physics class that light travels slower through glass than it does through air. Does this mean that light travels slower through matter of lower energy?

ANSWER:
Light in a vacuum is the fastest thing in the universe. Light traveling through any medium is therefore slower. The fact that light travels more slowly through a medium like glass is why lenses work. I do not understand what you mean by "matter of lower energy".

QUESTION:
Will carbon molecules hold an electric charge, i.e. could carbon be magnetised?

ANSWER:
Don't know just what you mean. Yes, you can make a C negative ion, that is add an electron to it. However, this has nothing to do with its being "magnetised". I think what you must mean is can you make carbon ferromagnetic. The answer is no since ferromagnetism depends on the crystaline structure of the material and the interaction of the outermost electrons with their neighbors, and it is most unlikely that you could make carbon do this. All materials are "magnetised" in some sense, either paramagnetic (attracted to a bar magnet) or diamagnetic (repelled); the effects are much weaker than ferromagnetism.

QUESTION:
If there are four fundamental forces--gravity, EM, weak and strong--how does the Casimir force fit in this scheme?

ANSWER:
The Casimir force has its origins in the electromagnetic force (vacuum fluctuations of the electromagnetic field). You can read a nice discussion at Physicsweb.org.

QUESTION:
If one were to release a standard, 20 lb., 8.5 x 11 inch sheet of white copy paper from, say, the space station, with adequate velocity to exit orbit and fall toward earth. Could it survive the trip? I seem to be the only one to believe that it could. The strongest claims against this theory so far have been meteorological- perhaps it becomes soaked with water, etc. what do you rhink?

ANSWER:
The possibility of water causing shoul not even be considered since, obviously, passing through a good thunderstorm could certainly cause the paper to go to pieces. The situation would depend on the speed at which the paper was moving when it hit the top of the atmosphere. For example if you just "dropped" it, that is caused it to fall straight down (which would actually mean giving it a velocity of about 18,000 mi/hr opposite the shuttle, I would guess it would make it since it would hit the atmosphere with a relatively small velocity. On the other hand, if you released it with just slightly less speed than the shuttle has but enough less to leave orbit, my guess is that when it hit the top of the atmosphere that it would "burn up" and be destroyed.

QUESTION:
i've noticed many similarities between gravitational fields and electric fields. Is there an analog in electricity to a black hole?, an infinite electric field with infinite charge at a point? If not, why not? If so, what sort of physical reproductions does (or would) this have on surrounding matter?

ANSWER:
The answer is no because a black hole forms because the gravitational force is attractive and so as you add more and more mass to an object it eventually collapses under the huge gravitational force (this is a bit of an oversimplification, but essentially how a black hole forms). The electrical force, however, is repulsive, so you the more charge you add the more the object wants to fly apart.

QUESTION:
is it possible to trap light in a box if it were filled with mirrors? and since things have color because of light ( ex.blue things reflect blue light and absorb all the others) when there is no light is everything actually invisible?

ANSWER:
Light would be trapped only for a very short time after which it would be absorbed by the mirrors (heating them up slightly); there is no such thing as a perfect mirror. For some numbers showing how quickly the light would disappear, see one of my previous answers. Regarding your second question, if you define "visible" as being able to be seen by the human eye, then, yes, things are invisible if there is no light.

QUESTION:
If the sun were to disappear in an instant, would the Earth spin off into space IN DARKNESS?? or would the "final light" from the sun, taking some 7-plus minutes to reach Earth, arrive prior to the "release" of magnetic pull/gravity occurrence as experienced on/by Earth? Perhaps my question has to do with the nature of gravitational pull--is it a "chain/rope"-sort of essence or some sort of wave, which would, I think, have to be at or less than the speed of light and means the light would go out first. I find my uninformed bias is toward the "rope" form, in which case we would by leaving orbit while the sun was still shining on Earth.

ANSWER:
The speed at which a gravitational field propogates has not, to my knowledge, been measured. It is generally believed that it propogates at the speed of light. Thus, the earth would leave orbit and go dark simultaneously. In any case, no physicist would believe that the appearance of any force would be instantaneous.

QUESTION:
Heres a physics question... I have a rubber band and three toothpicks. I loop the rubber band around two of the toothpicks, and hold them apart, stretching the rubber band. I have someone hold the two end toothpicks. I then slip the 3rd toothpick in the dead center of the rubber band, and start twisting it, winding the rubber band from the center. Then, I let go of the center toothpick, at the same time as my buddy lets go of ONE of the end toothpicks. The third toothpick is still held firm. The question is: Which toothpick spins faster, the center one or the end one. And more importantly, WHY? What physical theory causes this?

ANSWER:
First, since the the speeds will depend on when you look at them, let us revise your question so that we ask which will have the biggest acceleration at the start, that is which will acquire the greatest speed in the first short time. Your question is equivalent, at the beginning, to masses on springs. The middle toothpick is analogous to a mass attached to two identical springs, each stretched by some amount. The end toothpick is analogous to the same mass but attached to one spring stretched by the same amount. So when you first release them, the one with two springs has the greater acceleration. This will only be true immediately after release because the half of the rubber band between the two movable toothpicks will untwist faster.

QUESTION:
If you built a machine that would swing a weight and "kick" a ball along the ground, controlling all the variables, excepting that you double the weight, why would the distance the ball travel only be 30% more?

ANSWER:
You have not given me enough information about the machine, but a little consideration of the answer leads me to think that the machine must simply be the head-on elastic collision between two balls of different masses, one initially at rest. If the "kicker" has a mass M and incoming speed V, and the ball has a mass m and is at rest, then if you conserve both momentum and kinetic energy you will find the ball, after the collision, has a speed v'=2mV/(M+m). So, let us do two numerical examples:

If M=m, then v'=V.
If M=2m, then v'=(4/3)V.

Guess that answers your question since the distance the ball travels (while experiencing a constant retarding frictional force) is proportional to the initial speed.

QUESTION:
In the acoustic doppler effect, i have found that the higher the original frequency, the greater the shift in frequency.

ANSWER:
Quite simply it is because the frequency difference is proportional to the original frequency. In terms of a percentage change, there is no dependence on frequency.

QUESTION:
Does a hockey puck reach it's maximum velocity at the last instant of contact with the hockey stick, or is there such a thing as (for lack of the proper terminology) 'residual acceleration' I have considered this at great length.. >From what I know in physics if there is no longer force being applied to the puck there should not be any accelertion after the contact.... Almost a logical deduction.. however seeing replays and it's almost an instinct telling me that I might be wrong.. It doesn't feel like the stick is travelling at a the same velocity as the puck is.. 100mph shots and all.. Perception maybe different than reality.. anyway, if I am wrong and there the puck continues to accelerate for a short distance after leaving the stick,. it's because of the flex in the stick, the energy transfered into the puck has not fully caused it to accelerate.. possibly like the flex in a golf ball..

ANSWER:
A short answer to your long question: The puck cannot continue to accelerate (gain speed) after it leaves the stick. In the physics sense, it does accelerate but with a negative acceleration, that is it slows down.

QUESTION:
my question is how is the current flowing through the different resistors connected in series same f it is an axiom, then its ok. but if it has reason behind it,pls tell me

ANSWER:
No, it is not simply axiomatic. The reason is the conservation of electric charge. Consider just two resistors connected in series. A certain amount of electric charge enters one resistor in a certain time (electric current). Similarly, a certain amount of charge exits the other resistor. If the charge out is less (greater) than the charge in, where is the charge going to (coming from)? Electric charge cannot be created or destroyed, and since it is not piling up or being drawn from either resistor, the charge in must equal the charge out so the current in each is the same.

QUESTION:
I've always wondered if "time" is a man-made concept or if it really exists. I've heard that the fourth dimension is time, is this true?

ANSWER:
This is more a philosophy than physics question. As a physicist, I would say that time exists independent of my perceiving it. Our intuitive notions of time, such as that time is a universal thing throughout the universe for all observers is now known to be incorrect. Two identical clocks given to two different observers will definitely not run at the same rates if the observers are moving with respect to each other. This is the unavoidable consequence of the theory of special relativity. Time is the fourth dimension in the sense that when it is realized that time and space are entangled with each other, the result again of special relativity, the mathematics of the physics involving both space and time is very similar to the mathematics of a four dimensional space. For example, motion in three space may be described as a rotation in four space.

QUESTION:
A 50cm silver bar becomes shorter by 1mm when cooled.How much was it cooled? coeff. of linear expn=.000018/c. Which should be my original length ? 50cm or (50-0.1)cm?

ANSWER:
The equation you use, presumably, is DL=aDT=a(T_f-T_i)=(L_f-L_i). Since T_f<T_i you must have L_f<L_iso Li=50 cm.

QUESTION:
My cousin and I have a dispute about the flushing power of a standard 1.6 gallon flush toilet, versus an old-fashioned 5-gallon flush model. I use a lot of toilet paper, and therefore must flush 2 or 3 times with the newer 1.6 gallon models, or risk a clog, which has happened to me far too often. I maintain that the 5-gallon flush model will be much more likely to prevent clogs. Is there a formula for computing the pressure of a 1.6 gallon flush versus a 5.0 gallon flush? How would that be mathematically computed with precision?

ANSWER:
There is no reasonable way to compare them mathematically since they have different designs. The low usage one is supposed to be designed to have comparable disposal capabilities. Even if you are right that you, as an individual, must flush more than once, from a conservation point of view it would still be better to have an efficient toilet because you are likely not the only user. My son uses way too much paper also and every once and a while it clogs; I just pull out the old plumber's helper and in no time all is well.

QUESTION:
Hello, I have solved this question part of the way, but cannot figure out the end result! The question is: In an x-ray imaging system operating at 70 kVp, each electron arrives at the target with a maximum kinetic energy of 70 keV. Because there are 1.6 x 10^-16J per 1keV, this energy is equivalent to the following: (70keV)(1.6 x 10^-16J/keV)=1.12 x 10-14 J Inserting this energy into the expression for kinetic energy and solving for the velocity of the electrons, the result is: KE=1/2mv2 v2=2KE/m v2=(2)(1.12 x 10-14 J)/(9.1 x 10-31 kg) =0.25 x 1017 m2/s2 I can get that far....the end result is: v = 1.6 x 108 m/s If i use the equation v= mv2, I get: v = (0.25 x 1017) (0.25 x 1017)2 which gives me - v=(0.25 x 1017)(0.063 x 1034) and my answer comes out to v = 1.6 X 1051 m/s How do they get the answer v = 1.6 x 108 m/s ?

ANSWER:
This looks like a homework problem which the groundrules of my site prohibit! However, I will give you the hint you need: your expression KE=mv2/2 is wrong; this expression is true only for very slow (compared to the speed of light) particles. The correct expression is KE=E-moc² where E is the total energy, m_o is the rest mass, and c is the speed of light. E is given by E=(mo²c⁴+p²c²)^1/2 where p is the linear momentum given by mov/(1-v²/c²)^1/2. Also, your equation v=mv² is obviously incorrect because it could be simplified to mv=1 which is nonsense!

QUESTION:
My 11 year old has asked me, "Does gravity bend light?" I did highschool physics about 20 years ago, so am very rusty and not up to date with current thought. I have looked at this discussion topic on the archives of many forums, but have ended up very confused by the differing opinions/explanations. I would really like an answer which is easy to explain to a child, but yet not so simplistic that it is inaccurate. Am I asking the impossible? She has read about the nature of light and also about gravity, and can't understand how light can be affected by gravity, when it has no mass. Is it because photons are energy and so can be used instead of mass? Or is it that the gravitational pull around massive stars affects the "space" around it and light just follows the stretched paths? If this is true, how can some authors say that the light is still moving in a straight line even when it is following a curved path?

ANSWER:
Here is one explanation, probably the easiest for your daughter to understand: Light being affected by gravity is a result of the principle of equivalence in general relativity. This states that there is no experiment which you can perform to distinguish between your being in a gravitational field or in an accelerated frame of reference. Thus, for example, imagine that you are in an elevator which accelerates upward; if light enters through a hole in the side of the elevator it will clearly appear to fall like a projectile because of the acceleration of the elevator. So, the same thing will appear to happen in a gravitational field the acceleration due to which is exactly the same as the acceleration of the elevator. Hence, light will "fall" in the earth's gravitational field with an acceleration of 9.8 m/s². You might be interested in the answer to an earlier question.

Here is another: If we look at the world as having a Euclidean "flat" geometry and watch a ray of light pass a very massive object, we see the light bend. But, the way that general relativity describes the world says that, if we are in the vicinity of a massive object the space itself is not Euclidean but is curved; in this space the light follows a "straight line" in that non-Euclidean geometry.

QUESTION:
what is error on T when T = 1.04 * sin (2.8 ± 0.2)/ sin (58.2 ± 0.2)

ANSWER:
The largest contributor to the error will be the sine in the numerator since sine is small and changing rapidly at small angles so a relatively small uncertainty in the angle will lead to a large uncertainty in the sine of the angle. You can get a rough feeling for the percentage of the uncertainty by estimating the percent error of that term: (sin2.8-sin2.6)/sin2.8=0.071=7.1%. What you need to know is that the uncertainty of the sin(A±a) is approximately cos(A)*a (because d[sin(x)]={d[sin(x)]/dx}dx) and that the percent uncertainty of a ratio (A±a)/(B±b) is approximately a/A-b/B. Putting your numbers in I get about 6.7% (in accord with our rough estimate) uncertainty for T, or about ±0.004. {When you are doing your calculations it is important that angles (and their uncertainties) are expressed in radians, not degrees.}

QUESTION:
Does the flow of linear time as we percieve it (disregarding its pyschological variations) vary as you get down to the level of quantum mechanics? Secondly, if so, I've read at that level, all time is simultanteous, that it doesn't exist at all at that level. Is this true, and why?

ANSWER:
The answer to your question is that we do not know. Read my earlier comments related to this question. Regarding your second question, I never have heard it said that "all time is simultanteous" whatever that means. I have read that it is the opinion of some very deep thinkers that the reason that not much progress has been made in unifying gravity and quantum physics is that we really do not understand time very well.

QUESTION:
how is it possible that light can be both a particle and a wave! i need to know it's ruining my whole life.

ANSWER:
Ruining your whole life? How is it possible that my tie can be both red and green? That is just the way it is. I know that this is an unsatisfying answer, but science is based an measurements (experiments) and if you study light and look for a wave, you will find one but if you look for a particle you will find that also. This is called the wave/particle duality and it is, essentially, a statement of experimental fact. And you can do experiments which unambiguously see both possibilities in the same experiment. The best known example is to do a double slit experiment with very low intensity. If the intensity is so low that there is, say only 1 photon per minute passing through, then it has to pass through one slit or the other, right? Wrong--you still get an interference pattern. So, you say, light is therefore a wave, not a particle. But, imagine that the screen detects the light using the photoelectric effect which cannot be understood unless you treat the light as a collection of photons. This detector will work perfectly well in displaying the interference pattern. This duality is not unique to light: any particle will exhibit wave properties; e.g. that is how an electron microscope works, by exploiting the wave properties of electrons. Maybe I shouldn't have told you this since it may compound your life-ruining distress! Wave/particle duality is a reality of nature, that is all.

QUESTION:
A sample of a particular radioisotope is placed near a Geiger couinter, which is observed to register 160 counts per minute. Eight hours later, the detector counts at a rate of 10 counts per minute. What is the half-life of the material?

ANSWER:
This sounds suspiciously like a homework problem to me! However, I will outline how to do it but not do it to its final answer. The activity of a sample (counts rate) is an exponential function: A(t)=A0exp(-lt) where A(t) is the activity at time t and l is the decay constant related to the halflife by t=ln(2)/l. Since you know A at two times (I would call the first one t=0), this equation is actually two equations for two unknowns (A₀ and l), so you can solve for l which gives you t.

QUESTION:
WHEN A 1,000 POUND PLANE HAS WINGS THAT ARE BANKED AT 45* DURING A LEVEL TURN, THE CENTRIPETAL FORCE ON THE PLANE IS EQUAL TO THE WEIGHT OF THE PLANE. USE THE PYTHAGOREAN THEOREM TO FIND THE LOAD ON THE PLANE. [LOAD=WEIGHT+(CENTRIPETAL FORCE)]
A. ABOUT 2,000 POUNDS
B. ABOUT 707 POUNDS
C. ABOUT 1,414 POUNDS
D. ABOUT 500 POUNDS

ANSWER:
This looks suspiciously like a homework problem to me which are forbidden by the groundrules. However, it is sort of interesting to me because it doesn't make a lot of sense. I would have thought that load would be defined as the net force on the plane. However, load is defined here to be the horizontal component of the force the air exerts on the plane plus the weight (which is, of course, vertical). This force has a magnitude of the square root of 10002+10002, so C is the answer with the direction pointing 450 below horizontal. If the load were the force the air exerts on the plane, the answer would still have a magnitude of 1414 lb but would be in a direction 450 above horizontal. If the load were the net force on the plane the answer would be 1000 lb horizontal.

QUESTION:
Does the wavelength of light affect how brightly it shines?

ANSWER:
No, "brightly" is determined by the amplitude of the wave and not by its wavelength.

QUESTION:
What is light?

ANSWER:
Wow, that is a concise question. The answer is not! The nature of light has been of great interest over the ages. Once science became a legitimate pursuit (as separate from philosophy) the debate centered around whether light is some kind of wave or some kind of particle. Newton thought it was a particle; it was later demonstrated (in the early 19^th century}, however, that light behaves like a wave; see my earlier answer to a similar question for more background. What was actually doing the waving was a mystery until later in the 19^th century when Maxwell showed that light is waving electric and magnetic fields; again, see my earlier answer. Finally, at the beginning of the 20^th century Einstein, in explaining the photoelectric effect, found that light exists in quantities no less than what is called a photon, one quantum of the electromagnetic field. Hence, light really is like particles, a swarm of photons. We finally understand that light is both, a situation called the wave/particle duality; if you look for a wave you will find one and if you look for a particle you will find that also.

QUESTION:
do all orbits in space deteriorate? If not, why? Is it possible that the Earth's orbit could deteriorate (as well as Mars, etc.) and cause global warming trends?

ANSWER:
For an orbit to "deterioate" (we usually use decay to describe this), the orbiting object must lose energy. It can do this by colliding with stuff, mainly gas and dust so that the energy loss could be thought of like air friction on earth only much smaller. An orbiting object will also lose energy by radiating gravitational waves; this has been seen for some binary star systems. But, for the earth, these are totally negligible and certainly have no effect on global warming. The distance to the sun is much less influential than the angle that the rays from the sun hit us; we are actually farthest from the sun during summer.

QUESTION:
what would happen if there was too much air pressure?

ANSWER:
Well, you don't stipulate what "too much" is, so I will address an extremely increased pressure. The pressure due to the atmosphere is about 1 ton per square foot. So why doesn't this pressure crush you? The reason is that we have evolved in this environment so that the pressure inside our bodies is about one atmosphere; every cell in your body has a pressure inside which keeps it from being collapsed. Now suppose that you double the pressure outside. The pressure inside does not change and so you are crushed by the net force in on you. One of the first things to go is your eardrums which should not surprise you if you have ever dived to the bottom of a swimming pool where pressure increases fairly dramatically.

QUESTION:
My questions pertain to gravitational potential energy. Sepcifically, I'm a little confused about how it works. My understanding is that when an object is moved away from the earth (upwards) it gains gravitational potential energy that is transformed to kinetic energy if and when it falls back toward the earth. This understanding leads me to two questions. First, what happens to that potential energy once an object moves beyond the gravitational feild of the earth? Does that object still retain the potential energy it gained as it moved away from the earth? Second, why must I exert energy to hold something in a constant position relative to the earth? for example, why must I exert energy to hold a text book above my head. It is not moving towards or away from the earth, so is not gaining potential energy, yet I am exerting energy by holding it up against the force of gravity. On the other hand, a table does not exert any energy in accomplishing the same feat. So w hat gives? where does that energy go? Am I totally off base here?

ANSWER:
Your questions:

An object in a gravitational field never moves beyond the field since the strength of the field is proportional to 1/r² where r is the distance from the center of the earth. So there is never a place where the field is zero, just very small. The potential energy you are probably familiar with is mgy where y is the distance vertically from where you have chosen y=0. This works fine (but only approxiately) as long as y is much smaller than the radius of the earth; The correct potential energy is proportional to -1/r so as r becomes very large the potential energy goes to zero; but, note the minus sign: the potential energy gets smaller (more negative) as r gets smaller, so the potential energy becomes biggest when you are infinitely far away.
You are totally confused about what energy is. The way you impart energy to something is to do work on it, and work is a force exerted over a distance. You are exerting a force on the thing you hold over your head, but that force is not acting over a distance so you are not changing any energy. It makes no sense, from a physics point of view, to say that you "exert energy".

QUESTION:
Is it true or not that one can make larger structures such as planes, spacecraft (rotating) if we make the walls thicker? Does making the walls thicker enable one to build larger structures, without making them fall appart or deform?

ANSWER:
There is no answer to this question since what is necessary to make something bigger depends on what the thing is, what its location is, what it is made of, etc.

QUESTION:
This may seem like a strange question and one that cannot be answered without some sort of bias (religion, etc.), but if energy cannot be created or destroyed, where does the energy in a living creature go upon death? What other forms of energy is it transformed into, and what happens to the electrical signals in the brain and other parts of the nervous system?

ANSWER:
What energy is there in a living being? It is almost all bound up in the chemicals which make up the body. When it dies, the chemical energy either stays there or ends up as heat if the object decays. Regarding the electrical signals, an analogous question would be what happens to the light coming from a light bulb when you turn off the switch? The only reason the light bulb continues to glow is that there is a source of energy pushing electrons through it and when that source is removed the electric current simply ceases.

QUESTION:
OK, I have a sealed box with a 60W electrical fan inside. The fan just circulates the air inside the box. Does this box give off 60W of heat?

ANSWER:
A 60 W appliance is one which consumes 60 W of power, that is it consumes 60 J of energy each second. The appliance then converts this energy to another form of energy. For example, a toaster will convert most of the energy to heat (because it is designed to do that). A fan is designed to not convert energy into heat, but rather into kinetic energy (of both the fan and the air); the electric motor will heat up but not nearly as much as a 60 W toaster but probably more than a 60 flourescent light which is designed to convert as much energy as possible into light. But if your box is truly isolated from the rest of the world, much of the energy initially converted into kinetic energy of the air will end up as heat in the box and its walls.

QUESTION:
What is the math/calculations to transform volts/meter into newtons/coulomb?

ANSWER:
A volt is a joule/coulomb, 1 V=1 J/C. A joule is 1 kg m²/s², so 1 V/m=1 kg m²/s²/m/C=1 kg m/(Cs²).
A Newton is 1 kg m/s², so 1 N/C=1 kg m/s²/C=1 kg m/(Cs²).
So, 1 V/m=1N/C.

QUESTION:
why does the d- block in the periodic table have two valence electrons?

ANSWER:
This is really chemistry, not physics. I believe it is due to the following:

The first 20 elements have s- and p-shells. Beyond that, the ordering is not what you might expect. For example, you might expect, after 1s, 2s, 2p, 3s, 3p, are filled that next would come 3d. However, the 4s happens to have lower energy than the 3d so it fills first. Therefore, as the nd-shell is filling there are two electrons in the (n+1)s shell and these have wave functions which extend farther out than the d-orbitals and thus are more influential in determining the chemistry.

QUESTION:
How to shield an electronic circuit or laboratory from stray electric fields, and why does this work?

ANSWER:
Completely surround the circuit with a conductor. The reason that this works is that the electrons are free to move in a conductor. When the conductor is put into an electric field, the electrons move around in the conductor. All such charge (or lack thereof where electrons have left) will reside on the outside surface of the conductor and be arranged in such a way that the field due to these "induced" charges will exactly cancel out the field which induced them inside the volume enclosed by the conductor. This is called a Faraday cage (named after Michael Faraday who first constructed one). If what you want to shield is quite large, just enclosing it with a conducting mesh does a very good job as well. You should realize that this is true only for static fields; if the field changes with time, there will be fields inside the cage.

QUESTION:
If there was no cyntrifical force on planets... would there still be gravity?

ANSWER:
First of all, there is no such thing as a centrifugal force; I have repeatedly discussed that on this site and you can read a bit about it by going to older answers and searching (do a CTRL F) on centrifugal. The existence of the force of gravity is universal and the gravitational attraction between two objects is unaltered by anything else. Gravitational force between two objects results from their masses and nothing else. What you may be thinking of is that the apparent force of gravity is lessened somewhat by the earth's rotation. Imagine standing at the equator: you have an acceleration pointed toward the center of the earth of v²/R where v is the tangential speed due to the rotation (2pR/24 hr)=7.3x10^-5R and R=6.4x10⁶ m is the radius of the earth. Putting in the numbers, your acceleration would be a=3.4x10^-2 m/s². A force of ma is needed to keep you going around in circular motion and the source of this force is gravity. The result is that your apparent weight, the weight you read on a scale (which is actually not measuring your weight but is measuring the force the floor pushes up on you) would be slightly less than your actual weight. Since weight is mg=9.8m your apparent weight would be (9.8-0.034)m, about 0.3% less. If the earth rotated faster on its axis, this effect would be bigger and eventually your weight would not be sufficient to keep you in your circular motion and you would drift off into space. But the point is that your weight is always the same regardless of anything else--gravity is constant.

QUESTION:
how is the stella parallax angle of a distant planet or star calculated?

ANSWER:
I presume you mean stellar parallax. I recommend this site for a brief animated tutorial.

QUESTION:
When chemical bonds form, energy is released. Therefore, does water release energy as heat when it freezes? If yes, does this explain why it is warmer when it snows? Does the change of water from a gas to a liquid to a solid cause the ambient temperature to increase?

ANSWER:
You must add energy to melt ice. Therefore you must remove energy to freeze water. So, yes, water does release energy when it freezes. Similarly, water vapor releases energy when it condenses. However I doubt that these effects have any measurable effect on air temperatures. It is often warmer when it snows because the weather conditions favorable for snow (clouds, low barometric pressure) cause it to be warmer; in other words, the warmer (less cold) weather results in snow, not the other way around.

QUESTION:
While researching I found out At one time it was proposed to launch satellite directly into a circular orbit at a constant distant from earth using a giant WW cannon. Can you pleas tell me why this proposal would not work

ANSWER:
Assuming that we had a cannon capable of launching a projectile with sufficient speed (at least about 18,000 mi/hr), how would we aim it? One possibilty is horizontally. In principle, this could work. It was actually Newton himself who first imagined artificial earth satellites by proposing shooting a projectile off the top of a high mountain with sufficient speed. There is a good website where you can play around with launching satellites; if you set the speed to 16,000 mi/hr you should see a nice circular orbit. In practice this could not work, however, because the air friction due to the atmosphere at such a high speed would either burn the projectile up or cause it to slow down and hit the ground. If you aimed it up at some angle, the resulting elliptical orbit would intersect with the surface of the earth, that is it would crash before one complete orbit was completed. What you need to do is first lift your satellite above the atmosphere and then give it a horizontal speed with rockets on the satellite. So a simple projectile will not work.

QUESTION:
what would happen if a planet identical to Earth were to lie tangential to the earth, assume that there is no impact between the two heavenly bodies, one just appears. what would happen to gravity, the planets, the oceans, etc?
CLARIFICATION:
I meant that the crusts of both planets would be just barely touching.

ANSWER:
The gravitational field due to two spheres is the vector sum of the fields of each sphere. Hence, you could easily calculate the gravitational force at any point in space (in particular, of interest to you, on the surface of the earth) by just adding the forces due to each planet. A few simple examples would be:

At the point of contact the gravitational force would be zero, so if you were located close to this point you would be weightless.
Along a line tangent to both spheres and passing through the point of contact the force on an object of mass m (i.e. the weight) would be directed exactly toward the point of contact and wold have a magnitude of 2GMmd/(d²+R²)^3/2 where G is the universal gravitational constant, d is the distance from the point of contact, R is the radius of the earth and M is the mass of the earth. Note that this is zero if d=0 and approximately 2GMm/d² if d is much larger than R.
At the point opposite the point of contact, the weight of an object would be have a weight 10/9 times larger than if the new planet were not there and point vertically down.
At other points the weight would not point vertically down anymore because of the force from the other planet.

To compute these results you need to know that the gravitational force due to a uniform sphere of mass M on a point mass m a distance r from the center of the sphere points straight to the center of the sphere and has magnitude GMm/r² where G=6.67x10^-11 Nm²/kg² (only true if you are outside the sphere).

QUESTION:
The core of the earth is 'energized' by the compression of mass, since energy can be neither created or destroyed, where prior did this energy exist?

ANSWER:
The simple answer to your question is gravity. As a mass decreases in size its gravitational potential energy decreases and this energy loss is made up by energy gain, kinetic energy of the mass, that is it gets hotter. This is also how stars gain enough energy (temperature) to "ignite", gravitational collapse. It is thought, however, that part of the energy for heating the earth's core comes from the decay of radioactive nuclei in the core.

QUESTION:
Further on the "pull one end of a rope" idea - Do individual elemental particles with mass behave the same way? That is, do they have a "diameter", such that a force applied to say, the "right side" of say, a quark, will be "felt" on the "left side" of the quark an attosecond (or whatever) later?

ANSWER:
You have to be careful in extending classical ideas into the realm of the very small. In quantum mechanics, the appropriate way to describe subatomic physics, it turns out that the idea of force is not very useful. Rather we use the ideas of fields and potential energy. In classical physics, potential energy is easily related to force associated with the field. There is no useful way to define left and right but certainly the propogation of a field, responsible for forces, is not instantaneous.

QUESTION:
In the article here -- www.iop.org/EJ/article/0143-0807/27/2/017/ejp6_2_017.pdf -- the authors describe a process whereby sunlight is concentrated using the well known parabolic dish method, but afterwards is directed into a large sphere with a completely reflective interior. If one were to direct solar energy into a sphere of this nature, and closed the "hole", could one actually "store" the sunlight, and then let it out when needed?

ANSWER:
Well, I find I have no access to that article since I am not a subscriber to the journal. However, I do not need to see the article to answer your question. The answer is no, it is not practical to store light using mirrors. The reason is that a "completely reflective interior" is simply not possible and the light is quickly absorbed. To get some idea of the numbers involved, see one of my previous answers.

QUESTION:
In reference to singularities, etc., I do not understand the concept of "nothing". Since "nothing" is only understood as related or opposite to "something" it would seem that "something" is primary and "nothing" is imaginary. "Something" can be shown, while "nothing" can not be shown except in a relative sense. "Nothing" is only useful in a limited sense as a technique such as "zero". I think physicists use of "nothing" shows nonsense. "Nothing" is nonsense in and of itself since the thought of it alone, vis a vis "something", dissolves from the imagination. Therefore, the singularity is truly something but as yet not rationally described.

ANSWER:
I have no idea what your rant is about. I have never heard a physicist refer to a singularity as nothing. It has zero size but infinite density (for example if we think of a model for a black hole). And physicists were the first to realize that a vacuum is not empty at all but filled with virtual particles popping into and out of existence (see vacuum polarization). I should also note that most physicists I know do not believe that a true mathematical singularity is a physical thing because, although we might find "nothing" to be unphysical, we find the notion of something being infinite as abhorrent! However, the use of singularities in models is extremely useful and helps make our theories comprehensible.

QUESTION:
If I want to create a higher vacuum pressure in a container, than my vacuum pump can deliver, could I create that vacuum pressure by placing both the pump and container inside a second larger container, use the pump to evacuate both containers, seal the larger container off and then pump out the smaller container once more into the evacuated larger container. If my understanding of vacuum pumps is correct, they create a difference in pressure between the inside and outside of a given space, therefore it should be possible by placing one evacuated chamber inside another to multiply the pumps capability.

ANSWER:
The way a simple pump works is that it pumps an amount of air out, compresses it, and expells it. What determines the vacuum achievable is the rate at which air is leaking in (or outgassing from inside the vessel) since when you reach the point where the amount you take out in a cycle equals the amount that leaks in. It is not the pressure differential which is most important. The catch, however, is that if the vessel you are evacuating is in a low pressure environment, less gas will leak in. So my answer is yes and no--how's that for a hedge?

QUESTION:
Which will travel further when kicked a soccer ball or an american football. They are roughly the same weight, 410-450grams for a soccer ball and 421 for a football. I am assuming that the drag caused by the odd shape of the football will cause it to travel a lesser distance. Is there a way to calculate how much less either as a distance or percentage?

ANSWER:
This depends on a lot of things. However, the considerations I have thought of give the football an edge over a soccer ball. I will assume that each is launched with the same initial speed and angle. Were there no air drag, it would surely be a tie. Now, I assume that the football has been punted by a skilled kicker such that it spirals, that is spins around its lolng axis of symmetry. When this happens, as you probably know, it goes through the air pointy end first and is thus more aerodynamic than the spherical soccer ball. In addition, the soccer ball is relatively smooth whereas the football is knubbly. Although it is partly nonintuitive, a rough ball suffers less air resistance than a smooth ball because the rough surface carries a layer of air along with it called the boundary layer which helps reduce air friction; this, in fact, is why golf balls have dimples and tennis balls have fuzz. Finally, I can think of one way the soccer ball might have an edge: if the ball has a lot of spin in the right direction, lift will be generated (like in an airplane wing, or more analogously, a curveball in baseball). I doubt, however, that this effect will be as large as the effects which make the football go farther.

QUESTION:
What keeps an electron from crashing into a proton in an an atom?

ANSWER:
See my answer to an earlier question.

QUESTION:
If I google "einstein field equations" and go into the Wikipedia site, the bottem of the first page has "contents." I proceed to the section "The cosmological constant" and therein find a version of EFE with Lamda in it. It looks like this: Ruv - 1/2 R g uv + Lamda (guv) = 8 pi T uv. My question is this: Can I, in a mathematically valid (algebraic) sense, move every thing except Lamda from the left to the right side of the equation? More to the point, is it mathematically valid to say: l=(8 p T_uv + 1/2 R g_uv -R_uv) /g_uv I don't know if I'm breaking any geometric convention. Thank you for your thought.

ANSWER:
No, you may not do this. It is a matrix equation and you cannot divide by a matrix.

QUESTION:
How can force carriers affect two particles differently? For example: A virtual photon interaction between two electrons causes them to repel, but an interaction between an electron and an up quark causes them to attract. The photons are the same, so what is different about those two interactions that can cause different results? (I asked this question on another website, and I was told only that I was simplifying things too much. If I'm describing the process poorly, please let me know!)

ANSWER:
You are indeed simplifying things too much. The idea of particles passing photons back and forth is only a rough schematic picture of what happens. The particles, quanta, which convey a force (like photons do for the electromagnetic force) are not real particles (photons) but rather virtual particles. They are photons which cannot be directly seen, that is you could not stick a detector between the two charged particles and be able to detect them. Their existence defies energy conservation but that is ok as long as they "exist" for a short enough time; the reason is that it is, according to the uncertainty principle, ok for DE of energy to appear as long as it disappears within a time Dt where DEDt is less (approximately) than Planck's constant. There is a very nice discussion about virtual particles at http://math.ucr.edu/home/baez/physics/Quantum/virtual_particles.html

QUESTION:
Concerning gravity. I'm very confused (NB I,m 59 yr old NOT a student!) In a sphere (like a planet) if every atom is fully surrounded by similar atoms then, except at the surface, shouldn't gravity effects cancel out? OK, the heavier atoms will 'fall' to the centre but don't EM effects or the smaller atomic radii of metal atoms (so they will move through the planets core more easily) explain this? If centre of planet is a plasma, what does this 'do' to gravity? Has gravitational force of 'weightless' objects towards each other (eg in a spaceship) ever been measured? (OK I know it's very weak).

ANSWER:
Whoa, too many questions. The site groundrules state only single, well-focused questions, but I will go ahead this time and address some of your questions.

Imagine that you are the atom and you are one mile deep into the earth. Then if you look "up" you will see many fewer atoms than if you look down because it is a lot more than one mile through the whole rest of the earth. So you will still feel a force toward the center of the earth; it will however, be less than your weight on the surface. It is easy to calculate the weight of something inside the earth by the following trick: only that part of the earth inside where you are exerts a force on you. Hence, if the earth were hollow you would feel no force inside. Incidentally, your question is related to one of the most famous problems in the history of science. Newton delayed publishing his theory of gravitation for years because he could not be sure that the force between two spheres was the same as the force between two point masses at their centers. It is a very difficult problem and part of the reason he had to invent calculus was to solve this problem.
Regarding your second question: heavier atoms do not preferentially fall toward the center of the earth. If they did then lead and uranium would be at the core, then lighter and lighter atoms like onion shells as you went out until the lightest would be on the surface. This is not how it is. The reason is that all objects, regardless of their mass move the same way (with the same acceleration) in a gravitational field.
It does not matter what the composition of the center is as far a gravity is concerned.
You do not need to make the objects weightless to do this experiment. You just have to be careful to make sure that all other forces on the objects add up to zero. This experiment has been done many times. The classic experiment was that of Eötvös (see inset picture) done in the very early 20^th century. A group at the University of Washington has made many modern and very accurate measurements.

QUESTION:
I have a bunch of lasers and the manuals all say that the tubes will last longer if they are run a few hours a month. I used to work in analytical chemistry at an undergraduate lab and the chemist said that the gas filled tubes for the Atomic Absorption machine went bad if they weren't run all the time. However, I pulled out a hollow cathode tube that looked like it had never been used but was in a box that looked 30 or 40 years old and it was very strong. What is the physical reason for saying that gas filled tubes last longer if they are run "A few hours a month"? I have a degree in physics and have asked a number of PhD phycists and chemists this question and have not received even an attempt at an answer.

ANSWER: (Courtesy of Chad Fertig)
Running a discharge tube generates pumping action due to sputtering of the filament. This pumps away (some of the) background gasses that inevitably leak into the tube. An Ar/Kr Ion laser tube which hasn't been used in a long while will often need to be run at low-ish current (low enough to prevent overheating) until the pressure drops and the laser stabilizes to its normal operating parameters. If the background gas pressure gets too high, one may not be able to light the tube and not trip the overcurrent protection circuits. The laser engineers I have spoken with tell me that the shock of lighting a tube at high-pressure can be enough to kill the tube entirely. I don't know how much of this discussion applies to small atomic spectroscopy discharge tubes -- my experience is mainly with Ar/Kr Ion laser tubes.

ANSWER: (Courtesy of Uwe Happek)
One should run the laser periodically to activate a getter pump that traps unwanted aroms that slowly diffuse into the tube.

QUESTION:
If EVERYTHING in the Universe doubled in size...? .....would anybody notice? What about the square-cube ratio? The surface area of objects increases by the square, while volume increases by the cube. If you doubled the diameter of a planet and the height of the man standing on it, his mass would increase by a factor of eight and the mass of the planet by a similar factor. So the mans weight would be something like 64 times as much as before.while the cross section of his legs would only be 4 times as much. The burden on each square inch of his legs would be about 16 times the prior burden, without the extra strength to support it. It would be like suddenly standing on Jupiter. He would collapse and die very quickly by being 'squashed' to death by gravity! Obviously this is a purely theoretical question but if the 'known' Laws of Physics were applied to this, what would the answer be? I may have twisted my knowledge because it has been years since I studied. Simply take it that the universe has doubled (by magic?! :~} ). Would there be noticable consequences?

ANSWER:
I would not presume to make a blanket statement one way or the other for this question (because we physicists don't deal in magic!) I can, however, refute your specific example. You have forgotten that the radius of the earth would double and, since the weight is inversely proportional to the square of the distance, the weight would be only 16 times greater (64/4). Hence your new body would be ideally engineered to exist in your new environment.

QUESTION:
Light is massless and as such is the only thing can can travel at this speed. For any object with mass, it would take an infinite amount of energy to reach the speed of light. Therefore the speed of light is an unattainable goal! However, light can be caught by a Black Hole (I'm sure you know the phrase - the gravity is so strong that not even light can escape!). If light is without mass, how can it be caught by ANY gravity well? Astronomers have also proved that light 'bends' around black holes in a measurable and observable way. What can the gravity be 'pulling in' if there is no mass to light? Am I missing something?

ANSWER:
You are missing something--classical gravitational theory, where the force is proportional to the mass, is incorrect. Einstein's general theory of relativity is a theory of gravity which has withstood all experimental tests so far. The central idea of this theory is the equivalence principle which states that there is no experiment you can do by which you can determine whether you are in a gravitational field or an accelerating reference frame. For example, suppose that you are inside a box with no windows and you drop a ball and it accelerates down with an acceleration g=9.8 m/s². Are you at the surface of the earth or in the middle of empty space in a box which is accelerating with an acceleration g in a direction opposite the direction you see the ball accelerate? There is no way you can know without looking out a window. Now do a similar experiment where you stand at one side of the box and shine a beam of light across the box; it will follow a parabolic trajectory down if the box is accelerating up, that's for sure (although for such a small acceleration, it would be very difficult to observe; see one of my earlier answers). The equivalence principle thus asserts that the beam of light will "fall" in a gravitational field.

QUESTION:
There is a rope, say 20 mile long, and a person pulls the rope from one end, point A. Question: Will the other end, point B, move instantly or will it take time?

ANSWER:
It takes time. Basically, atoms in the rope are held together by the electromagnetic forces between atoms and electric fields propogate with the speed of light, so a very rigid strong rope would take a pretty short time for the other end to start moving. A more stretchable rope would take longer.

QUESTION:
How many tons of TNT would it take to be able to stop an asteroid with a mass of 7.2e15 kg moving at 2436 m/s? Would we assume that the collision is ellastic or inellastic and would we use the priniciples of the conservation of energy or conservation of momentum?

ANSWER:
You are approaching this question in such a way that there is no way to answer. It depends entirely how the "bomb" of TNT is configured and is a very complicated question. You can do some calculations:

the kinetic energy of the asteroid is about 2 x 10²² J
the linear momentum of the asteroid is about 1.8 x 10¹⁹ kg m/s
the energy content of TNT is about 4 x 10⁹ J/ton

Probably the best way to approach how to stop the asteroid is to consider momentum. The time rate of change of momentum is equal to the force applied, so suppose you pushed on the asteroid for a year with a constant force such that it stopped at the end of the year. Then the force would be (1.8x10¹⁹)/3.2x10⁷)=5.6x10¹¹ N=1.26x10¹¹ lb. The rate at which energy is expended is the energy change divided by one year, (2x10²²/3.2x10⁷)=6.3x10¹⁴ W. This is bigger than the entire energy consumption rate of the US, about 10¹³ W.

What you should be figuring out by now is that it is totally impractical to talk about stopping this asteroid. When people discuss how to protect us from collisions from asteroids, the idea is always to make a very small change in its path a relatively long time before it would hit us. That means a rather small change in momentum thereby requiring much less force. For example, suppose you wanted to change this asteroid's trajectory by 0.01⁰. Then the momentum change would be about sin(0.01)x1.8x10¹⁹=3x10¹⁵ kg m/s. If you had an explosion which lasted 10 s, it would have to supply a force of 3x10¹⁵/10=3x10¹⁴ N=6.7x10¹⁴ lb. This is still a pretty big force, you will agree. Here the energy increase would be about 6.5x10¹⁴ J so the power over the ten seconds would be 6.3x10¹³ W which, although still pretty huge, could probably be achieved with a thermonuclear device over a few seconds. I guess my message here is that making big changes in the motion of something as large as an asteroid using brute force methods are simply not possible with technology we have .

QUESTION:
If the maximum velocity of any particle or electromagnetic radiation is the speed of light and if light and other forms of electromagnetic radiation cannot escape a black hole, then how could Hawking radiation be possible?

ANSWER:
Hawking radiation has nothing to do with what the speed of the radiation is. The radiation, the existence of which is still controversial, is due to esoteric quantum effects which are too technical for this site.

QUESTION:
Is it possible for a material to act as a superconductor at absolute zero. I understand that matter can become superconductive at temperetures around absolute zero, but I am unable to find a definative answer as to whether or not this happens at absolute zero.

ANSWER:
Well, acheiving absolute zero is not physically possible, so you need not concern yourself with what happens there. However, you may approach arbitrarily close, so it is meaningful to ask what happens in the limit of very small temperature approaching zero. If the material is known to be superconducting it has undergone what is called a phase change where the resisitivity of the material suddenly drops to zero at some temperature. Then the resisitivity would remain zero as temperature approached zero. If the material did not undergo a phase change, it would not be superconducting in the limit as temperature approaches zero.

QUESTION:
How much one cubic inch of sugar cube weigh?

ANSWER:
I looked up the density of granulated sugar, from which sugar cubes are made, and found 849 kg/m³. From this you can find, by using standard conversion factors, that the mass of one cubic inch of sugar is 13.9 g or a weight of 0.491 oz.

QUESTION:
If you took a radio antenna and had the technology to generate a eletrical AC signal across the antenna with a frequency of around 6*10¹⁴ Hz, would you see visible light coming from the antenna, or would it just be a really fast oscillation of energy between eletric and magnetic fields? If it would produce visible light, would similar frequencies give IR and UV and so forth?

ANSWER:
You would see nothing. There might be some EM radiation in the visible region but the intensity would be too small to "see". The problem is that the antenna must have a size comparable to the wavelength corresponding to the frequency for it to have any appreciable intensity. The wavelengths for visible light are hundreds of nanometers and so you would need to have an antenna comparable to the size of an atom. In fact, atoms do act like little antennae and that is where we normally get visible light.

QUESTION:
If a fine liquid filled capillary tube is place horizontally and both ends are immersed in the same liquid as that filling it, is the pressure at the midpoint of the tube larger than that at the ends?

ANSWER:
Although I do not know a lot about capillaries, I do know Newton's first law. If the pressure were greater in the center than the left end, the fluid in the left half of the tube would have a net force to the left which it cannot since it would be in equilibrium. What I do know about capillaries is that they depend on the meniscus to drive the fluid through the tube and there would be no meniscus under the conditions you state.

QUESTION:
I actually have an idea that isn't possible currently, but I'd still like to suggest it to you, because I'm vey concerned about the effect of the greenhouse effect on mankind. Seeing how things are going with it right now, time for all life on earth may be running out faster than we think, and we MUST do something more than just fighting oil companies emissions... Now to the point - I't is finally time that people in the physics community would take a chance at designing and building at least a working model of an ozone particle regenerating machine. For the sake of the earth and mankind, I think it's at least worth a good try.

ANSWER:
The ozone problem and the greenhouse effect are not the same thing. The greenhouse effect comes from too much CO₂ in the atmosphere which traps the energy which light brings from the sun. The ozone problem is that ozone is needed as a shield against incoming ultraviolet radiation from the sun but is depleted by introduction of chemicals which interact with it (like chlorofluorocarbons in older refridgerants). I believe that restrictions on these chemicals is making noticable effects in solving the ozone problem. Regarding your suggestion, building any machine which can have any kind of effect on something as huge as our atmosphere would be an undertaking which would cost our entire GDP and more!

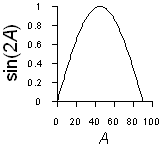
QUESTION:
Why is a 45 degree angle the best angle to shoot a water baloon to get it to go the fartherest distance?

ANSWER:
See my earlier answer pertaining to projectile motion. Inasmuch as the range R of a projectile may be shown to be R=v²sin(2A)/g where v is the speed at launch, A is the angle of launch, and g is the acceleration due to gravity, you can see that the range is proportional to the sine of twice the launch angle. At 45⁰ the sin(2x45)=sin(90)=1 which is the biggest the sine can be.

QUESTION:
What exactly do scientists mean by "folding a spectrum through a filter transmission profile" ? What is folding?

ANSWER: (Courtesy of J. Scott Shaw)
In astronomy it means multiplying the intensity of the spectrum by the transmission % of the filter at each wavelength to get the resulting intensity at the detector. Or you can do it from the detector to the spectrum, depending on how you need to see the problem.

ANSWER: (Courtesy of Richard S. Meltzer)
I think this refers to the alteration of the actual spectrum by the transmission of a filter so that what is observed is so modified by the filter transmission. If one knows the transmission of the filter as a function of frequency, one can deduce the actual spectrum from the observed spectrum by dividing the observed spectrum by the transmission of the filter.

QUESTION:
a light bulb uses 60J of energy to give 6J of useful heat energy. true or false???

ANSWER:
False. An incandescent light bulb is only about 5% efficient, that is 95% of the energy goes into heat. Your question is sort of strange because I wouldn't call heat useful energy. We usually use a light bulb for light, not heat, so it is the light which would be thought of as useful. If the question had said "useful light energy" instead, it would not have been far off.

QUESTION:
Can you tell me the wavelength of the EM wave that would correspond to the photon emitted when a hydrogen atom's electron falls from the n2 to the n1 energy level?

ANSWER:
121.566 nm. See http://hyperphysics.phy-astr.gsu.edu/hbase/tables/hydspec.html

QUESTION:
I am learning about half-lives and am curious: is it possible to shorten the half-life of radioactive decay?

ANSWER:
The short and practical answer to your question is no. The half life for the transition from one state of a system to another is determined only by the wave functions before and after (a wave function is a mathematical construct which contains all the information about the system). However, if you were able to change the wave functions by changing the environment, you could change the half life; for example if you put the radioactive nuclei in a very strong electric field you would change the wave functions. However, the force which holds the nucleus together is so strong, it would be virtually impossible to make a noticable change in this way. What is more conveniently done is to transmute the original nucleus: for example, if you add a neutron to a radioactive nucleus you would likely form a new radioactive nucleus but with a very different half life. This has been discussed as a way of dealing with radioactive waste from reactors.

QUESTION:
Is there any very important reason too why a coulomb is 6.24x10 exponent 18 electrons? i do not know very much about the coulomb

ANSWER:
The Coulomb (C) is defined in terms of the Ampere (A). The Ampere is an electric current carrying 1 C/s. The Ampere is operationally defined in terms of the magnetic force between two current carrying wires. So the answer is that the fact that there are a certain number of electrons in a Coulomb has no significance.

QUESTION:
In nuclear reactions, when they are bombarding atoms with a neutron n for example, How do they get just a neutron (fission) by itself to hit at a certain velocity?

ANSWER:
You are referring to nuclear fission reactions in a reactor, I presume. Every time one of the fuel nuclei splits into two pieces, it also releases several fast neutrons. These neutrons may then be used to cause other nuclei to split and so forth. This is called a self sustaining reaction--once you get it started, it will keep going as long as one or more neutron, on average, causes another fission. The problem is that fast neutrons have a very low probability of being captured by a nucleus and are most likely to just fly away; if we slow them down, however, they have a high probability of causing another fission (simply because a slow neutron spends more time passing through a nucleus than a fast one). So we must slow them down for the reactor to work. The way that this is done is to introduce a moderator which is efficient in slowing them down. Good moderators are water or graphite.

QUESTION:
Besides being released in beta decay and making up for the excess of mass when a proton+electron are froce to bcome a neutron what does the elementary particle "neutrino" actually do??

ANSWER:
What do you mean by "do"? The question is more appropriately "what are the neutrino's properties?" To get a full discussion of neutrinos I would recommend the Wikepedia article.

QUESTION:
What is the formula for the range of a projectile?

ANSWER:
Neglecting air friction and assuming that it lands at the same height at which it was launched, R=v²sin(2A)/g where v is the speed at launch, A is the angle of launch, and g is the acceleration due to gravity (9.8 m/s²). You can find plenty of derivations of this formula on the web by googling "projectile range".

QUESTION: ;
We say that centripital force is centre-seeking and that it pulls the rotating object to the centre of rotation. If this is the case then what force is responsible for pulling the object outwards. For example, with a yo-yo rotating in a horizontal plain. The tention in the string pulls the yo-yo inward, keeping it from flying off. However, what is the force that causes the yo-yo to extend outard? Is this the centripital force? If so then doesn't this mean that centripital force pulls outward on the yo-yo while the force of tension pulls inward on the yoyo?

ANSWER:
A ball going around in a circle has an acceleration pointing toward the center of the circle. Newton's second law thus says there must be a force pointing toward the center of the circle and this is called the centripetal force. Any number of forces with components in that direction may contribute to the centripetal force, but the simple example you give has just the tension in the string providing the centripetal force. There are no other forces (in the horizontal plane) acting on the yoyo. Your statement referring to the yoyo "extending out" makes no sense; if the string breaks the yoyo does not fly radially outward but continues in the direction of its motion at the instant the string breaks. If you imagine yourself to be the string, there will be a force outward on you which is equal in magnitude to the tension in the string. This is because of Newton's third law: if one object (string) exerts a force on another object (yoyo) then the other (yoyo) exerts an equal and opposite on the first (string). But this outward force is not on the yoyo.

QUESTION:
According to Einstein's special theory of relativity ,velocity of light is a universal constent .It does not change with respect to observers velocity relative to the source of light .But I had heard that Doppler effect occurs due to the relative velocity between the source and the observer .Then if relativity theory is true,why doppler effect occurs?

ANSWER:
You have answered the question yourself. The postulate says that the speed is constant, not that the frequency or wavelength are. The frequency or wavelength of light does depend on the motion of the observer.

QUESTION:
I am a teacher and I was wondering how I can address students' misconception that weight does ot affect accleration due to gravity. We did several controlled experiments to determine the variables that affect the speed of a car rolling down a ramp. In one experiment with a car and ramp, the weight was changed as the car was timed from point A to point B. Some groups of students found that sometimes the more weight added to the car, the faster it acclerated down the ramp, while other groups found that the more weight added, the slower the car rolled down a ramp. So now they are confused. How can I steer them away from this misconception?

ANSWER:
The design of the experiment must take into account all the variables. One of the most troublesome variables in doing mechanics problems is friction and I am sure that changes in friction as you change other variables is what is causing trouble here. So, I propose the simplest of all experiments to convince them that acceleration is independent of mass if it is the only (nonnegligible) force present: just do Galileo's experiment of dropping a marble and a bowling ball (or some similar pair) simultaneously and see them hit simultaneously. This would be most effective out of a second floor window, but you can drop them from six feet in the classroom and have a pretty convincing experiment. Of course, you could also use a feather and a bowling ball but the feather would be the loser by far, not because of its (smaller) weight but because of its (larger) frictional force. At a nearby college or university you might be able to borrow an apparatus in which there is a feather and a marble inside a glass tube which, if you pump the air out, the two will fall with the same acceleration. If your students understand Newton's second law you might find my previous discussion of this problem helpful. Another experiment you could do if you have access to an air table is to use it for your races and minimize friction.

I helped my son with a pinewood derby a couple of years ago and I can tell you that it is not easy to understand the physics of these little cars. One thing which is often noted is that the fraction of the wheels rubbing on the axels is quite important and using graphite as a lubricant often speeds them up.

QUESTION:
How much evergy is released, when a drop of water changes its shape from a cube to a sphere of the same volume? How much is the drop getting warmer as a consequence of it?

ANSWER:
The work done in changing the surface area by dA is ydA where y is the surface tension which, for water-air interface near 20^o C is about 73x10^-3 N/m. The surface area of the cube is about 24% larger than the sphere with equal volume (which I am assuming is easy for you to show). So the energy released is about 0.24x73x10^-3xA where A is the area (4pr²) of the sphere. For a sphere of water with radius 1 mm I estimate an energy of about 2.3x10^-7 J. I will leave it to you to compute the temperature change for this amount of water when this amount of energy is added; you just need to calculate the mass m of the drop and set the energy equal to mcDT where c is specific heat of water and DT is the temperature change.

QUESTION:
I made this question up myself when pondering how to teach Newton's 3rd law: A pulse of electricity through a wire produces an electromagnetic field that travels outward at the speed of light. This field encounters a charge and exerts the appropriate forces on it. While the forces are occuring on the charge, on what is the reactionary 3rd law force? I believe that the closed loop nature of the fields would render the net work done as zero.

ANSWER:
Here is a dirty little secret we never reveal to our students in introductory physics: Newton's third law is not always true! Particularly in electrodynamics, it is rather easy to see in simple examples. The culprit, as you seem to have intuited, is the magnetic forces. As a simple example suppose you have a particle (#1) of charge q moving in the positive x-direction with speed v along the positive x-axis and a particle (#2) of charge q moving in the positive y direction with speed v along the positive y-axis. Particle 1 sees a magnetic field pointing in the negative z-direction due to particle 2 so it experiences a force in the positive y-direction; particle 2 sees a magnetic field pointing in the positive z-direction due to particle 1 so it experiences a force in the positive x-direction. Of course, each particle also experiences a repulsive electrostatic force but these do obey Newton's third law. But the net force does not. If the magnetic forces involved were due to magnetostatic forces, long steady currents, Newton's third law would be obeyed (as in the well known force between two long parallel current carrying wires on which the definition of the Ampere is based). It turns out that for the electromagnetic field, one must include energy and momentum densities of the fields themselves to do Newtonian mechanics and then all is well. If you want to pursue this further, I would recommend the intermediate-level E&M book by Griffiths.

QUESTION:
My question regards a discrepancy between answers I get when I work a problem using two different approaches. This problem was given to me several years ago, and although I got the right answer then, I was told that I could have also used a different approach. I have tried several times since to do this problem the other way, but have had no luck. The problem is this: if a pole of length L is stood on end and released, if the initial velocity is neglegible, what is the final velocity of a point at the end of the pole when it hits the ground. I believe I originally solved this problem using the concept of the potential energy being converted to kinetic energy (mgL=(1/2)mv2), getting an answer of v=(2(g)(L))^(1/2). I am now trying to solve it using calculus by integrating the equation v2=2ad over all da from 0 to 9.81m/s2 (where d is the arc length of the falling pole), and taking the square root of both sides. When I do this I end up with an answer of v=(( PI)(g)(L))^(1/2). What am I doing wrong?

ANSWER:
Neither of your methods is correct. The second method, using v²=2ad is wrong because this equation is valid only if the point has uniform acceleration which it does not. The first method is incorrect because you treat the stick as a point mass at the end of the stick falling straight down which is not what is happening. The only way to solve this problem in closed form is to use energy conservation as you have tried to do; however, you must use rotational dynamics to do this. So the potential energy at the beginning is mgL/2 because the center of mass of the body is located halfway up the stick; the kinetic energy when the stick hits the ground is Iw²/2 where I is the moment of inertia of a the stick about its end (which is ML²/3 for a uniform stick of mass M and length L) and w is the angular velocity of the stick (which is v/L if v is the speed of the point at the end). If you now equate the energies before and after and do the algebra, you will find v=(3gL)^1/2.

QUESTION:
Do physicists believe that the world is continuous or discrete? In other words, is there a smallest distance a particle can travel and/or a smallest increment in time?

ANSWER:
This is an open question. Although nobody has seen any evidence for the discreteness of space or time, many serious theorists, particularly those working in quantum gravity, believe that there does exist a distance which is the smallest possible distance called the Planck length. This length is on the order of 10^-35 m so it is not surprising that there is no experimental evidence for it since this is 10^-20 times the size of a proton! Similarly, time is thought to have the smallest possible duration which is the time it would take light to travel the Planck length, also very small.

QUESTION:
What guarantees that human made particle colliders won't create black holes eventualy as they reach higher and higher collision energys? I ask this because if i understand it correctley, black holes aren't created only out of the large mass of the stars that go supernova, but they are created by the large density that the large mass of the star creates in it's center when the atoms if its center collapse. What i mean is: The star that went supernova was heavier than the black hole it creates, yet it is not a black hole. So this means that black holes are created by their large density and not their large mass. This is why i want to know wether particle colliders could create a (dangerous) balck hole here on eart, beacause they also, like supernovas make atoms collapse into great densitys.

ANSWER:
The possibility of a black hole being created is still speculative, but there is the real possibility that a tiny black hole (say 300 proton masses) may be created. However, black holes do radiate energy (called Hawking radiation) and such a black hole, if it were to exist, would totally evaporate in an unimaginably short amount of time, before it would have time to suck up any mass.

QUESTION:
If you were in a black room with no doors/windows/external light sources and every part of your body was the same shade of black as the room and you lit a match, would you see your shadow? Would you see your own hand?

ANSWER:
I presume that by "black" you mean something which is a perfect absorber of electromagnetic radiation. In that case you would not be able to tell if light is falling on it or not by using your eyes as you usually do, i.e. by seeing the reflected light. On the other hand, the energy carried by the light would have to go somewhere and it would show up in increased temperature of whatever absorbed it. Now, all objects radiate electromagnetic energy but, in your example, things look black not because they are not emitting any electromagnetic waves but rather that nearly all this radiation is outside what eyes can see (in the infrared). But the catch is that a perfect absorber is also a perfect radiator, so all the energy from the lighted match will be reradiated but mainly in the infrared so you couldn't see it. If you had an infrared detector you would be able to "see" the shadow, etc.

QUESTION:
I just moved to an area with snow and find that whenever it is snowing in the night, there is always this orange-ish "ambient light" that seems particularly bright, bright enough that one can see fairly well to the point where one can drive slowly without headlights in unlit areas. i am wondering what is the source of this light. i am fairly sure that it is not moonlight (there is light even when the sky is covered with clouds, and the intensity of the light does not seem to change during with moonphase). It might be street lights reflecting off the snow, since the color of the light is orange-ish, but then again you can see this light even when you are dozens of miles away from big cities, and the intensity of the light does not seem to change as you travel further from big cities.

ANSWER:
I feel pretty sure that what you are seeing is what astronomers call light polution. The characteristic orange color you are seeing would indicate that the source is sodium vapor lamps, often used for city street lights. The light, particularly if it is not directed toward the ground and is transmitted upward can scatter from snow, water vapor, dust, smoke, etc. in the air so that you can see it quite readily even at surprisingly large distances from the city of its source.

QUESTION:
All of the physics examples for gravity and projectiles depict freefall or horizontal/angular from fixed start locations, eg: a ball dropping over a cliff or a cannon shooting a ball. And I understand the results. However, I have been unable to find any answer regarding specific vertical scenarios. For example, if we are standing in an elevator that is not moving, and drop a ball, it freefalls at 9.8 m/s/s. So we can easily calculate the time from when it is dropped to when it hits the floor. But what would occur if the elevator were moving upwards at a constant velocity (not accelerating) of 2.5 m/s (the average elevator speed), and you dropped a ball. Would the time for both balls to hit the floor be identical? If the ball in the upward moving elevator maintained a constant vertical velocity of 2.5 m/s during its freefall lifetime in addition to the applied force of gravity I would think that they would... However, I would assume that the vertical velocity of 2.5 m/s would not remain constant for the lifetime of the ball's fall, as gravity is directly opposing that upward velocity. The ball's vertical upward velocity should decrease as a curve due to the gravitational force applied in the exact opposite direction. Similar to what would occur with a projectile that is fired vertically, the upward velocity decreases and it then falls back down accelerating due to gravity. Now since the elevator's floor is still moving upward at 2.5 m/s, the ball dropped in the moving elevator should hit the floor first.

ANSWER:
The motion of the ball is the same in any frame of reference which moves with constant velocity relative to the stationary elevator. The dropped ball in the moving elevator takes precisely the same time to reach the floor as it did when the elevator was not moving. To help you understand this, keep in mind that when the ball was released in the moving elevator, it had a speed of 2.5 m/s upward as seen from the ground. Basically, you are touching on what is called the principle of relativity, namely the laws of physics are the same in all inertial frames of reference; an inertial frame of reference is any frame which moves with constant velocity with respect to a frame of reference (for example your stationary elevator) in which the laws of physics are true. If your elevator had been accelerating upward with an acceleration of 2.5 m/s/s it would have been a different story. In this case, the ball would appear to fall with an acceleration of (9.8+2.5) m/s/s and hit the floor sooner.

QUESTION:
I have a question regaurding light and energy. It is known that it is impossible to accelerate a particle as fast as the speed of light due to the fact that it would take an infinite amount of energy. However, a photon's energy is difined as E=hf, where h is the product of Planck's constand and f is the frequency of the photon. So, why can light have a finite amount of energy whereas an accelerating particle can not?

ANSWER:
The photon has no mass and therefore it is exempt from this rule (as is any massless particle). All massless particles necessarily travel with the speed of light and they are not accelerated to get there, they are created already going that speed.

QUESTION:
Okay, hypothetically speaking, if there was a chain strong enough to not break under the ridiculous amount of stress and the chain was attached to the moon and the earth (probably by a mad scientist) what would happen? Would the moon slowly be drawn into the earth? Would the earth wind itself up in the chain as it rotates upon it's axis and how fast would it wind up? would the chain have to be built on the moon and lowered to earth? How would the chain be affected by earth's gravity when it first hit the atmosphere? If it was possible what type of material would the chain be and how thick would it need to be? Would it heat up as it cut through earth's atmoshpere?

ANSWER:
When you first start, there is no need for the chain to be strong because the moon is held in its orbit by gravity and any additional force (the tension in the chain) would disrupt that orbit. To see this, imagine the earth and moon to be point masses and there is a weightless chain between them;there is no tension in the chain. Now, let's get a little more real: no chain is weightless and so there would be tension in it just to support its weight but it would vary from point to point and still exert no force on the earth or the moon which would continue to orbit each other as if the chain were not there. Now, let the earth become its normal size. Since the earth rotates once on its axis every 24 hours but the moon goes once around the earth every 28 days, the chain would pull the moon down like a fishing reel. There is an analogous thing which has been discussed, having an "elevator" into space (not as far as the moon, but farther than where communication satellites are). Here, both to support its own weight and the weight it carries up, the cable would have to be very strong. It has been suggested that perhaps the cable could be fabricated of carbon nanotubes. You might be interested in the Wikepedia article on space elevators.

QUESTION:
I know that the length of an organ pipe (as well as the speed of sound in air) determines the frequency of sound produced within it. Does the diameter of the pipe have any effect on the sound produced?

ANSWER:
What the length determines is the fundamental frequency, but no musical instrument contains just the fundamental. each note played by each instrument also contains what are called overtones, other frequencies, usually simple multiples of the fundamental. The relative intensities of the many frequencies produced is called the timbre and it is what allows you to tell the difference between an A played on a violin or an organ or a trumpet etc. Geometrical properties of organ pipes other than its length determine its timbre; design of organ pipes has evolved from trial and error and, as such, is more an art than a science.

QUESTION:
What exactly is oscilating when we're talking about the wave nature of a particle? What are the bounds in which between it oscilates?

ANSWER:
There is not a physical wave which you can visualize. It happens that something called the wave function, which is intimately related to the probability of the particle being found at some place at some time, satisfies a wave equation. This equation, however, is not the usual one since its solutions are necessarily complex, that is they contain both real and imaginary parts. An imaginary number, the square root of negative one, cannot be physical but often is very useful mathematically in describing the physical world. To extract what you actually observe in nature from the mathematics requires having techniques which remove the imaginary parts of quantities. So, the oscillating is of a complex quantity and, as such, is not visualizable.

QUESTION:
Suppose you are given two iron rods, and you are told that one is a magnet and the other is not. Using ONLY those two rods, how would you determine which was a magnet and which was not?

ANSWER:
If you, at some distance away, align one bar (A) perpendicular to the other (B) and pointed toward B's center and bring it closer it will experience a strong force along its direction if it is the magnet; this is because it will attract B and Newton's third law says that A will feel an equal and opposite force. On the other hand, if A is not the magnet, it will find itself in a magnetic field which is nearly uniform and perpendicular to its length, so it will become magnetized in the direction of the field; however, a magnet in a uniform field feels no force so it will experience very little force. I am assuming that the magnetized bar is a simple dipole, that is one end is north and the other south.

QUESTION:
what keeps electrons energetically orbiting a nucleus?

ANSWER:
What keeps a satellite orbiting the earth? What keeps the moon going around the earth or the earth going around the sun? In all cases, once you give an object the energy required for a particular orbit, conservation of energy keeps it from changing. If the earth were to suddenly stop moving and drop into the sun, it would have far less energy; where did that energy go? To change the orbit you need to add or subtract energy to/from the object. What is particularly interesting about an electron in an atom is that an electric charge running around in a circle radiates energy (that is what an antenna is) and so the energy should radiate away and the electron fall into the nucleus. However, it does not and this observation started the whole branch of physics called quantum mechanics: one of the laws of nature is that bound objects are allowed to exist only in specific (quantized) energy states and therefore, if in such a state, a particle cannot radiate its energy away except all at once by going to a lower energy state. There is, however, a lowest state (called the ground state) and if the atom is in that state, it must stay there.

QUESTION:

Is nanomolecular technology able to create a dimond saw blade from the carbon in the air?
Are nanobots able to create things out of carbon?
What would happen if Carbon was broken down again? (that is, carbon is an element, but can you destroy or break it down futher?)

ANSWER:

The only way to make diamond is under extremely high pressures, so one could not just coat a saw blade with carbon in the air and expect it to be diamond.
Nanobots are still in a very experimental stage and so what they can or cannot do is open to question and interpretation. Most nanobots which exist have the purpose of detection of something, for example bacteria or particular chemicals. I don't think there would be a reason why, someday, a nanobot couldn't fabricate things out of carbon or anything else.
Normal carbon(¹²C)is composed of 6 protons, 6 neutrons, and 6 electrons. You could make anything you like out of those 18 particles. Some examples:
- 6 hydrogen atoms and 6 free neutrons.
- 3 helium atoms
- 6 "heavy hydrogen" atoms

However, this kind of rearrangement takes much more energy than chemistry and is not easy to do. The reason is that the force which holds a nucleus together is the strongest force in nature so it is tough to break nuclei apart. You could do some "chemical" type breaking apart with much less energy by ionizing the atom, for example remove one electron and you have a singly ionized carbon ion. You might find the Wikepedia article on nanobots interesting.

QUESTION:
When accelerating from a stop with your car door open, the door swings shut. Now given that the force applied to the door is thru its pivot point there should not be a net torque on the door, so it shouldn't move. To idealize the situation I have imagined an axle with a rectangular mass attached accelerated (normal to the axle) in deep space to negate gravity and air resistance. I'm thinking the "door" would not pivot in this case, so that the pivoting experienced in the original case is due to air resistance, some kind of unbalance of applied forces, or maybe even the fact that the car is not an inertial frame.

ANSWER:
Idealize the hinge to be frictionless. Then there is no torque about the hinge. However, the hinge can exert a force on the door (or else it would be left behind when the car accelerated). The direction of this force is forward so that, according to Newton's second law, the center of mass will accelerate forward, as you know to be the case. Now, ask yourself if there are any torques about the center of mass of the door. There is the forward force which the hinge exerts and this exerts a torque which will cause an angular acceleration about the center of mass. If you sketch that force, you will see that the torque will tend to close the door. You were right to be suspicious of whether the car and the door not being inertial frames might be a problem. You may not apply Newton's laws in noninertial frames but there are special exceptions, the most important being if you ask about what happens in a frame attached to the center of mass; even though not inertial, Newton's laws remain vaild in this frame. That is why, after asking what forces there were on the door, I switched to the center-of-mass frame.

QUESTION:
I am teaching physics at a Kansas high school, and my students and I were debating over a problem. The problem is as follows: Two 20-N boxes are placed on both ends of an ideal rope. The rope is then passed over two pulleys fixed on each of the two edges of a fixed table, so that one 20-N box hangs on one pulley, and the other 20-N box hangs on the other pulley (the rope being continuous over the two pulleys). We have been debating over the value of the tension in the rope, whether it's 20 N or 40 N. Half of the class agrees with me that the tension is going to be 20 N, but I cannot convince the rest of the class that the tension is not 40 N, but rather, 20 N. (Or is it me who's wrong?)

ANSWER:
Breathe easy--you are right! The tension in this rope is 20 N. The tension at a point in a rope is defined as the force which it exerts on what it is attached to. So you need to focus on one box or the other. You now say, what are all the forces on that box? One is its own weight which we know to be 20 N vertically down. Another is the force which the rope exerts on it; technically we know neither the magnitude nor direction of this force, but it is called the tension in the rope at the point of attachment. There are no other forces on the box. Since it is in equlibrium, all (both) forces must add to zero, so the tension is 20 N straight up. And, for a rope of negligible mass the tension must be the same everywhere on the rope; otherwise if you inserted a tiny mass in the rope and the tension were different on one side than the other, the tiny mass would not be in equilibrium.

QUESTION:
I attached magnets (round, penny-size, strong) magnets to each of the three blades of my small wind turbine and a two-inch opposite magnet stick to the pole for more power to push the blades. Then I placed the wind turbine into a wind tunnel to test if if it generates more energy than without. It did generate less energy...please explain why. Do I need a stronger magnet stick ?

ANSWER:
As each magnet on the turbine approaches the stationary magnet it is attracted but as it goes away from the stationary magnet it is still attracted, so this force will cause the turbine to alternately speed up and slow down so you will get no net work from the magnets. Technically, you should have gotten the same energy output but your experiment probably increased the friction of the turbine and so you lost energy there.

QUESTION:
if you are in a train traveling half the speed of light, and another train on a separate, parallel track, was approaching you, also at half the speed of light, would you see the passing train travel past you at the speed of light?

ANSWER:
Classically, that is what you would think. But the theory of special relativity shows that velocity addition in classical physics is wrong but you can only easily see that it is wrong at very high speeds and half the speed of light certainly qualifies! The speed you would see the other train approaching would be 80% the speed of light.

QUESTION:
When boiling distilled water in a pot, bubbles rise from the bottom. What is within those bubbles? Would it be oxygen? If so, is the oxygen extracted from the water? What happens to the hydrogen excess?

ANSWER:
When a liquid is heated enough it transforms into a gas (this is called a phase transition). The bubbles you see in a boiling liquid are simply little volumes of gas within the liquid, so in your question there is just water vapor inside the bubbles.

QUESTION:
If you were to drop an ice cube and a shot glass from 4 feet up, which would land and break first? Why?

QUESTION:
My question to you involves the feather and bowling ball freefall experiement in a vacuum. Now I understand that by removing the factors of air resistance that you free up the feather to fall much faster than it normally would. But the part I'm having trouble with is that they do indeed fall, gravity is obviously still involved and the ball still outweighs the feather many times over. In fact the term "weight" is defined by the amount of force gravity exerts on an object's mass. (not totally clueless, I just look like I am) So by that term should not the ball fall much more quickly since gravity has that much influence on it?

ANSWER:
Since these two questions are so similar, I will answer them with one answer. Ignoring or removing air friction results in all falling objects as having the same vertical acceleration, 9.8 m/s/s; that is the speed of any freely falling object increases by 9.8 m/s as each second ticks by. Hence, the ice cube and the shot glass and the feather and the bowling ball will all hit simultaneously. To understand the "why" you need to know two things:

Newton's second law states that the acceleration of an object is proportional to the force it experiences and inversely proportional to its mass; if we define a unit of force to be that which causes one kilogram to have an acceleration of 1 m/s/s, then a=F/m if F is in Newtons.
An object's weight, the force which the earth exerts on it, is proportional to its mass. So we can write that W=mg where, for now, g is just some constant; if we measure the weight in Newtons and the mass in kilograms, then we find (by simply measuring) that g=9.8 m/s/s.

Putting these two things together for the case where the force in Newton's second law is the weight of an object, then a=W/m=mg/m=g. Note that m cancels out; this is the key to understanding. Although the weight is proportional to the mass, the inertia (resistance to acceleration) is also proportional to the mass, so all objects have the same acceleration.

QUESTION:
Water is attracted to each other right. So when you cut through ice are breaking this attraction. I mean what happens when you break something or cut something at the atomic/molecular level.

ANSWER:
In a solid, each molecule is bonded to its nearest neighbors. The nature of the bond is very complicated, but is similar to the bonds which bind molecules together. When you break a solid, you break all such bonds which were along surfaces which appear.

QUESTION:
I am writing in the interest of hopefully resolving a question which had arisen in my workplace. One gentleman poses the hypothetical situation of a motionless tank sitting on solid ice which he describes as "very slick and smooth - so much so that if one were to toss a penny across the surface then it would glide on endlessly." He posits that the tank is then started and attempts to move forward. His position is that the tank will not be able to move as the treads would simply spin on the ice. His detractor posits that the treads are moved by the wheels inside the treads and that this would be able to propel the tank forward. So, would this tank be able to move forward or not? If so, what propertys of physics would make it be able to move and, if not, why would this tank not be able to move forward? The gentleman's scenario also posits that there is no friction between the tank treads and the ice. Is it realistic, physically speaking, to posit these two surfaces touching and no friction existing between them?

ANSWER:
How genteel you are! The gentleman who says that the tank will not move forward if the ice is perfectly frictionless is correct. It is the force of friction which accelerates the tank forward, not the force which the wheels exert on the treads; if the wheels exert a force on the treads, then Newton's third law says the treads exert an equal and opposite force on the wheels so the two cancell each other out. No it is not possible to have a perfectly frictionless surface; it is possible to get a good enough approximation, however, to do an experiment which should convince the second gentleman.

QUESTION:
I assume that the "big bang" theory is correct, but to accomodate the concept of infinity, it must be that this process is repeated or cyclical. After the universe expands for quite some time, gravitational pull will eventaully slow down the speed of expansion until it stops, and then gravity will create an accelerating contraction when all matter returns to a single space and time, when another "big bang" takes place. While the universe is contracting, history and time go backwards, and we live our lives again in reverse, and all cosmological events are repeated in reverse order. This theory provides for infinity, and also for the concept of "eternal life", that would be a cyclical event, half the time going backward, but repeated for all eternity. Eternal life in this way may not be just a religious belief. I don't know the math involed, but this may be the "unified theory" unsolved by Einstein.

ANSWER:
Your basic premise, that the universe is fated to collapse back on itself is not necessarily true. If the universe has more than a critical amount of mass, it will eventually fall back; if it has less than that amount of total mass, it will keep going forever. Determining which of these possibilities describes our physical universe has been one of the main quests of astrophysics for many years. However, recently observations have been made that the expansion of the universe is actually accelerating, so it seems more likely that the universe will not collapse as you posit.

QUESTION:
What happens to all the light photons that enter your eyes?

ANSWER:
For the most part, they vanish giving their energy to heat or chemical reactions which initiate nerve impulses which your brain detects and interprets.

QUESTION:
Why do high voltage devices (power lines, transformers, etc) hum? They have no moving parts to vibrate, so what causes the humming?

ANSWER:
If there is sound, then obviously something must be moving. The hum you hear is usually 60 cycles (since that is the standard for AC) and results from electric currents interacting with magnetic fields. Suppose you have a thick wire which carries a current; then there will be a magnetic field everywhere around that wire, including inside it. The current will interact with the field and will experience a force which causes it to move and since the frequency of the field is 50 Hz, so is the motion (in response the the force) of the wire.

QUESTION:
if two people are moving past each other at a constant speed in an infinite empty space, to either one the universe would be static and the other person would be in motion (relativisticly). if two people were at a constant unmoving distance from each other, but one of them was rotating at a constant speed, to either one the universe would be static and the other person would be in motion, correct? so if they were far enough apart, wouldn't the rotating person see their friend travelling faster than the speed of light (tengentially)?

ANSWER:
The two situations are not equivalent. Assuming that in your first scenario each was an inertial frame (one in which Newton's first law is true), then both are inertial frames and each can rightly claim that he is at rest. In the second scenario, if one is an inertial frame then the other (revolving around it) is not, so the rotating frame cannot claim to be at rest.

QUESTION:
I recently heard that if you shoot a bullet straight out with one hand and drop a bullet to the ground from the same height with the other hand then both bullets will hit the ground at the same time. Is this true and why. It would seem that the bullet being shot would have much more energy behind it abd take longer to expend that energy and hit the ground.

ANSWER:
This is what happens assuming that there is no air friction (which is actually a pretty poor approximation for something going as fast as a bullet). But, if there were no air, they would hit simultaneously. The reason is that they both move identically in the vertical direction, that is they both have the same acceleration vertically whereas the one shot moves with constant speed horizontally. So, imagine having a horizontal spotlight which cast a shadow of the shot bullet on a screen, a way of looking separately at its vertically motion. The shadow would move in exactly the same way as the dropped bullet.

QUESTION:
If the earth were to see an extreme increase in mass, would it colapse and form a black hole?

ANSWER:
That depends on how big an increase of mass. If big enough it could collapse because of the gravitational force.

QUESTION:
i am working on a pendulum and i want to know how the shorter the lenght of string the quicker a pendulum completes a period? Could you also tell me how the lenght of the string affects the period of a pendulum?

ANSWER:
The pendulum is a standard problem which any elementary physics text will explain in detail. If the amplitude is small (it does not swing through too big an angle), the period is approximately proportional to the square root of the length; for example, if you make the length 4 times longer, the period will be twice as long.

QUESTION:
If one places a lightbulb inside of a mirrored chamber, such that all surfaces other than the lightbulb itself are made of the best mirrors available, then turns the lightbulb on, does the chamber get brighter and brighter? What will happen eventually? During this process, if one open the chamber, will he see a flash of light?

ANSWER:
The answer to your question is that, even if the mirrors were extremely reflective, say 99.9% of the light was reflected, and since light travels so incredibly fast, a pulse of light is gone before almost any time has elapsed. It might be helpful for you to read an answer to an earlier question sort of like yours.

QUESTION:
My friend and I are arguing over which science one should study first. I say chemistry because it is a "central science" which helps one understand other sciences, but he says physics does this. Any thoughts?

ANSWER:
Physics is more fundamental than chemistry; scientists generally say that if you understand something in terms of the laws of physics, you understand it from "first principles". So you are right, from a philosophical perspective and physics should be studied first. Chemistry may be thought of as applied atomic and molecular physics. But, most educators would agree with your friend as can be seen in any high school science curriculum; chemistry should be taken first. The argument for this point of view is that physics requires much more mathematics to do properly, that is, chemistry can be understood empirically without knowing a lot of mathematical details. If you are good at math and have had enough of it, then physics might be better to take first. Actually, I took physics first in high school and fell in love with it!

QUESTION:
I was recently watching a programme about the Hubble Space Telescope and the pictures it had captured. It mentioned that the pictures it captured were of galaxies forming millions of years ago-If this is so- Could it then be possible for man, should he a find a way to manipulate space travel, be able to position himself at a certain area of space, at a certain distance and witness the birth of the milkyway itself? or indeed the birth of Earth?..........perhaps even the birth of man?

ANSWER:
Suppose that something happened here on earth 500 years ago and you were located at a distance of 500 light years from the earth with a very good telescope. Then you would be able to witness that event right now. But, here is the rub. You cannot get there from here before the light from the event reached there because it is physically impossible to travel faster than the speed of light; in other words, you could get there in just under 500 years and you would be able to witness what happened here tomorrow.

QUESTION:
My family is astounded with long thin projections of ice that form regularly and randomly on top of ice cubes since I began placing the ice cube trays in the freezer door. Even when the door is unopened from the time the trays are filled until the time the ice is well hardened, the needle like spears that usually slant in various directions at about a 45 degree angle, still form. Some of these projections reach a length of about an inch. On some cubes there are large fat lumps that raise up somewhat like a low volcano. The trays are stacked one on top of the other and the cubes in the bottom one does not, of course, have these curious growths. Can you explain how this happens?I

ANSWER: (Thanks to Professor Craig Wiegert)
I've also witnessed this phenomenon. (Unfortunately, automatic ice makers seem to be largely immune to this curiosity, so it's been several years.) The creation of these ice spikes has to do with the fact that the ice cube freezes from the outside in. The top surface starts to "crust over" first, with the ice growing outward from the edges of the cube (in the same way that lakes freeze over in colder climes). Meanwhile, the sides and bottom of the cube also start to freeze. Because ice is less dense than water, the growing "skin" of ice starts to crowd out the unfrozen water at the center of the cube. The water has nowhere to go but up. If the top surface of the cube is mostly frozen except for a thin spot in the middle, the water will be pushed out of that opening to form a bump. When the conditions are right, the "bump" will instead become an ice tube (freezing from the outside in, remember) and the water will be able to rise even higher. The end result is the ice spike. Better descriptions, with lots of nice photos, movies, and some experimental results, are available at:
http://www.its.caltech.edu/~atomic/snowcrystals/icespikes/icespikes.htm
and
http://www.physics.utoronto.ca/~smorris/edl/icespikes/icespikes.html
The best example I ever saw was in my family's backyard birdbath when we lived in Oregon. A cold front had swept through overnight, and the next morning we found an ice spike at least 4 inches tall protruding from the center of the basin. There's probably a picture tucked away somewhere in a family photo album...

QUESTION:
In deriving the equation for pressure of an ideal gas, is the force exerted by a gas molecule on the wall given by change in momentum/time between coliisions or change in momentum /collision time?

ANSWER:
You do not actually want the force delivered by an individual molecule but the average force per molecule averaged over many collisions. If you knew the time per collision, you could add many collisions, divide by the number, and find the average force per molecule. But, if you watch a single molecule and find the time between collisions for that molecule, you will find the same result without having to know the details of the collision itself. You get momentum transfer per unit time which is force due to that molecule.

QUESTION:
When matter and anti-matter come into contact,is the destruction complete.Do no elementry particles remain?? Is it just "gone"?

ANSWER:
Many different things can happen. The best known matter/antimatter annihilation is when an electron and a positron, both at rest, annihilate. In order to conserve energy, two photons come out (photons are essentially light, electromagnetic radiation but with no mass). Since physicists think of photons as elementary particles (even though massless), the answer to your question is no. If one or both of the electrons have energy (are moving), it is possible for new particles (with mass) to be created in the process. The most important thing is that the energy (including mass energy, mc²) must be identical before and after the "destruction".

QUESTION:
If you were to drop two equal boxes of equal dimensions built with the same material and you filled one with ping pong balls and the other with bricks. You than proceded to drop them both simaltaneously out of an airplane at 2000 feet. Which one would hit the ground first and why?

ANSWER:
In an elementary physics course you are taught that all objects have the same acceleration, so from that perspective the motion of the two boxes would be identical and they would therefore hit the ground simultaneously. However, in the real world there is air friction which is normally neglected when you first learn about free fall. However, air friction is not negligible particularly if speeds get very large. So, as you stipulate, the geometries of the two objects are the same, they will both have equal air friction for a given speed. However, when the air friction force equals the weight of the object, it will stop accelerating and fall at constant speed; therefore the lighter box will stop accelerating sooner and therefore hit the ground later.

QUESTION:
Hi! Why doesnt an electron emit radiation as it goes around the atom is it not really accelerating? Does the equal + and - charges make the dipole invisible.

ANSWER:
This may be an unsatisfying answer, but it doesn't because it doesn't! The problem is that our laws of classical physics do not work at very small distances (or at very large speeds). It turns out that an object must be described in terms of its "wave function" which is, essentially, a statement of the probability of finding it somewhere. When you do the calculations using the branch of physics called quantum mechanics, the wave function is zero unless the electron is in only certain states (including the ground state), so the probability of finding it in a slightly less energetic orbit (as it would tend toward if radiating energy away) is zero; hence, no radiation. An alternative way to look at it is to say that the electron should be thought of as a wave; it turns out that the wavelength of the wave is exactly right to fit in the orbit so the wave interferes constructively with itself (just like a vibrating guitar string). However, for a different orbit, the wave each time around "destroys" itself.

QUESTION:
My wife and I were in a car accident last night and I want to know how many G's our bodies withstood. I weigh 175 and she 140. We were hit from behind at a speed of 65-70 mph while at a complete stop. I was driving a 4Runner and the woman who hit us was driving a Dodge Caravan. I'm afraid I don't have the exact weight of each vehicle.

ANSWER:
That question cannot be answered. It depends on how long the collision lasted, whether the cars stuck together, how fast each car was going after the collision, etc. The information you have given me is mainly irrelevant to computing your acceleration (g's). Here is how you could make a rough estimate: suppose that after a quarter of a second you were going 20 miles per hour having started from rest. Then your average acceleration would have been (20 mi/hr)x(1 hr/3600 s)x(5208 ft/1 mi)x(1 g/32 ft/s²)/(0.25 s)=3.7 g.

QUESTION:
I’m a PhD student in philosophy interested (but not working in) the philosophical foundations of relativity. I have a couple of questions dealing with the speed of light and special relativity. The main question is number 3, the other two are auxiliary. Your response would be greatly appreciated. I will also greatly appreciate it if you could let me know whether there is some bibliography available dealing with this kind of issues.

Why is the relativistic length contraction – as it appears in the Lorentz transformation – a function of the speed of light?
Conceptually, it is possible that the speed of light had a different value than it actually has. How would that have affected special relativity (in particular length contraction for fast-moving bodies)? I recommend your looking into the Mr. Tompkins in Wonderland books by George Gamow.
Suppose we will discover a "form of light" (call it light*, symbolized c*) whose speed is double the speed of light, and it is also invariant. This would enable us to send signals at this speed and to use these signals to synchronize clocks so that we may provide an empirically meaningful definition of simultaneity. Do we need to revise special relativity and base the Lorentz transformation for length on this new value (c*), instead of c? Which of the following possible responses should be the case and why: a) we can do that; b) is it impossible to do that; c) we must do that.

ANSWER:

The answer is that the fact that light has the same speed in all frames of reference leads to this result. It is simple algebra and, if you are seriously interested, you should take the time to learn the basics of special relativity.
Special relativity would have the same form it does. If the speed of light were 100 miles/hr, effects like time dilation and length contraction would be everyday phenomena which we would not find puzzling at all. I recommend your looking into the Mr. Tompkins in Wonderland books by George Gamow.
This seems extremely unlikely since light is just a manifestation of electromagnetism and its speed is predicted by Maxwell's equations. For a new kind of invariant speed to exist, there would have to be another fundamental force in nature the theory of which predicts radiation of that speed. Since there is no good quantum theory of gravity, that is a remote possibility; gravity waves, however, have never been directly observed although their existence has been inferred from energy loss of binary systems. It is usually assumed that gravity waves move with the speed of light, but that is unverified. Regarding your simultaneity question, there is never any problem defining when two events are simultaneous. The problem is that events simultaneous in one frame of reference are not simultaneous in other frames; having some other universal speed is not going to change that.

QUESTION:
Why there is a weightlessness in an artificial satellite?

ANSWER:
See the answer to the following question.

QUESTION:
I always wondered about this question and was hoping you can shed some light on it for me. I noticed on Star Trek, they have gravity on their spaceships. I know this is a sci-fi program and realize its all fictional based on some scientific facts. But, I always wondered , why can't we put gravity on the spacestation we have orbiting our planet now? I know we have simulated 0 gravity on earth. Why can't gravity be simulated on a spacestation in space?

ANSWER:
The only way we know to "simulate gravity" is to be in an accelerating frame of reference. If you are in a frame accelerating down with an acceleration of 9.8 m/s² near the earth (e.g. a freely falling elevator) you will feel weightless. That is why you are weightless in the space station because it is in free fall, just like the elevator but it is a free falling projectile. To create "gravity" you would have to have a local acceleration of 9.8 m/s²; the way to do this is to have a very large donut shaped space station (say maybe a few hundred meters across) which is rotating with the right speed so that you could walk around the inside of the outer surface feeling as if there were gravity.

QUESTION:
Suppose a star is 2 light years from earth. A ship leaves earth and travels to the star and then returns to earth. If the ship travels at very close to the speed of light , it should take close to 2 years for the trip, as measured by someone on earth. But would the time for the trip be close to 0 , as measured by someone on the ship? Mathematically, if t is the time for the trip, as measured by someone on the ship, and v is the velocity of the ship, does t tend to 0 as v tends to c ?

ANSWER:
The answer to your questions are "yes" and "yes". Of course, you made a small mistake in that it would about take 4 years to make the round trip at close to the speed of light. You might be interested in my previous discussion of the twin paradox.

QUESTION:
Why does light travel faster than sound? In Grade 11 physics, I am learning that everything that goes through the same medium should travel at the same speed.

ANSWER:
It is incorrect to say that everything that goes through the same medium has the same speed. When I walk through air, I don't go at the speed of sound. Maybe what the idea is is that all waves traveling in a particular medium have the same speed. The medium through which sound travels is air and all sound waves go (approximately) the same speed. However, when light passes through air, air is not the medium through which allows it to travel, that is if we take away the air, the light will still go through but the sound will not. Finally I should note that even the statement that all waves in a medium have the same speed is incorrect. The speed which a wave moves through a medium depends on its frequency; this is called dispersion and is why a prism splits white light into a rainbow.

QUESTION:
According the Law of Conservation of Mass (or matter), matter is neither created nor destroyed, it simply changes form. So, when a baby is gestating, where do the atoms that make up that fetus come from? My thought is that the matter is coming from two sources: the sperm and egg to begin with, and from the food that the mother is ingesting to nourish the fetus. (And I suppose the air she is breathing contributes to the nourishment of the fetus.) Would that be correct? I figure that's where new plants come from....they pull atoms of nourishment from the ground and that helps build the plant itself.

ANSWER:
First of all, there is no such thing as conservation of mass. Energy is what is conserved and matter is a kind of energy (you know, E=mc²). The idea of conservation of mass is a 19th century concept and comes from chemistry where it is generally assumed that if you have a certain mass of hydrogen and the appropriate mass of oxygen and if they combine to form water, the mass of the water will equal the sum of the masses of hydrogen and oxygen. However, if you could make an accurate enough measurement, you would find that the water had a little less mass than the hydrogen plus oxygen (because you must put energy in to break the water apart and it shows up as mass in the end). That said, the forces holding molecules together are incredibly weak and so the change of mass in chemical reactions is incredibly small, so, for all intents and purposes, mass is conserved. And therefore, you are right that the mother supplies all the mass (after conception). And, yes, plants get their mass for growth from the ground and the air.

QUESTION:
I am investigating a factor that affects the period of a conical pendulum, so after a little theoritical work* I decided to vary the lenght of the cord while keeping other variables constant. My question is "does the initial speed affect the period?" and What is the best way to design this experiment using simple lab equipments?
* I came up with this formula>
T = 2pi*sqrt(L*cos(a)/g)
T = period
sqrt = square root of ()
L = lenght of the cord
a = angle between the cord and the vertical

ANSWER:
Your equation is right. The initial speed does not appear in the equation, but the motion certainly depends on it because for the pendulum to be a conical pendulum with a particular angle a, it is necessary that the speed be just right. Hence, v is "hiding" in a. In fact, you should be able to show that v=sqrt[(Lg sin²(a)/cos(a))]. Design your experiment so that you can vary L as well as a so that you can measure T and compare experiment with theory. The tricky part might be launching it with the right speed at each angle; trial and error is probably ok.

QUESTION:
The Heisenberg Uncertainty Principle states for a photon that: (certainty of energy)*(certainty of lifetime)=k If a photon's speed is always = c, then a photon can't age. My question is: if photons don't age, then how can there be uncertainty about their lifetime?

ANSWER:
"Aging" has nothing to do with anything here. Also, you should state the uncertainty principle in terms of uncertainties, not certainties. In the case of a photon, its energy is exactly hf where h is Planck's constant and f is the frequency of the associated electromagnetic wave. Hence, the uncertainty of the energy is zero, so to obey the uncertainty principle, the uncertainty of the lifetime is infinite; as you know, photons are stable particles.

QUESTION:
Electrons have two possible states, spin up and spin down; no one electron is forbidden from changing from one state to the other, yet how does an electron create the energy from within to change states?

ANSWER:
For an isolated electron, there is no energy difference between the two states.

QUESTION:
if i understand correctly light travels at a fixed speed, and so it takes, for example, 8 minutes for sunlight to travel to earth. if this is so, is everything is see in the past, allowing for the light's travel time? and if so, is an object i see at 50 metres closer in time than an object seen at 100 metres?

ANSWER:
This is certainly right. In simple physical terms, when you make a physical measurement you must make allowance for the time of transit of the information to you.

QUESTION:
When I studied the force of gravity in a college physics class, I always wondered how one object could exert a force on another object or how one "knew" the other was there. Later, in trying to understand Einstein's general theory of relativity I came to understand that gravity is not due to objects acting upon each other but rather from a distortion that occurs in the geometry of space-time (like the bowling ball on the trampoline idea) which results in the illusion of an attraction. More recently, I've been reading about a particle called the graviton which physicists hypothesize travels back and forth between massive objects at the speed of light resulting in the "attraction". So, which one is it? The distortion of space-time or the "messenger" particles zipping back and forth? Or both? And if both, how do the two concepts fit together?

ANSWER:
The operative word here is "hypothesize". The idea of a graviton is based on expectations that we should be able to understand gravity from the perspective of quantum physics. However, there is no remotely successful theory of quantum gravity and it remains one of physics' "holy grails". The theory of general relativity is very successful but not reconcilable with quantum mechanics.

QUESTION:
The discussion is if there was such a thing as a indoor wakeboard training facility would the hydro dynamics be such that if water speed was equal in the following scenarios could equal amounts of 'big air' be obtained.

A 200# wake boarder is being towed behind a boat at a distance of 60' at 20 mph. The wake height is 24" high and has a 45 degree angle on the outside of the wake. The wake boarder has sufficient skill to cut in from outside the wake and obtain a height of 36" and travel 20'. Rope mounting height is 36" above water level.
The same 200# wake boarder is in a wave pool capable of creating the same water conditions as being towed behind a boat at a distance of 60' at 20 mph. Same wake characteristics and same skill level from the same wake boarder. Will the Wake boarder be able to obtain the same height and distance as he would behind a boat? Same rope, rope height same everything.

Some of us say yes some say no. Some are of the opinion that forward momentum generated by the boat would enable greater distances to be obtained. Others say that the height and distance would be equal because it is the speed of the water going by and the ability to generate speed perpendicular to the direction of the water that provides the speed to obtain height and distance.

ANSWER:
You are going to have the water going by in #2 with the same speed as the boat in #1--good. You are going to have a wake with the same characteristics (same height and motion relative to the wakeboarder)--good, although I am not convinced that it would be easy to actually do this since the wake shape has to be essentially at rest relative to the wakeboarder whereas the water per se is not. What you do not talk about is the air. In #1 there is a significant wind in the face of the wakeboarder so you better have a big fan for #2. I believe that air friction will play a very important role after he lifts off, that is he will essentially fly like a ski jumper. I think that if you don't forget the air, it will be a pretty good simulation. Incidentally, the boat has nothing to do with the mechanics of the wakeboarder because they are not in contact so the boat cannot exert any forces on him. Whatever happens to the wakeboarder depends only on his interactions with water, air, and rope (and, of course gravity).

QUESTION:
around 1930, Dirac solved electron spin and magnetic moment by treated the electron as a point particle. i ask, is the electron a point? what is meant by a point particle?

ANSWER:
To the best of my knowledge, nobody has measured a structure of an electron, that is it really appears to be a point particle, something which occupies zero space. However, most scientists I know are uncomfortable with infinities in nature and such a particle would be infinitely small and have infinitely large density (because it has nonzero mass). Another aspect of your question is that elementary particles all, as you know, exhibit wave-like properties and as such the meaning of "size" becomes sort of fuzzy.

QUESTION:
Regarding the Stern-Gerlach experiment of 1922 concerning space quantization, does this mean that electrons come in two flavors, spin up and spin down?

ANSWER:
Spin up and spin down have meaning only if up and down have a meaning. Hence, you must first choose a coordinate system in which to make measurements. When you do this, you may say that electrons have two possible states, spin up and spin down. However, a particular electron may be in a state which is a combination of some probability of each. Quantum mechanics is weird!

QUESTION:
Given the length of a column of air in a musical instrument changes the frequency of the note (shorter column, higher pitch), I assumed that this was why adding water to a wineglass changed its frequency when made to "sing". However, on reflection, adding more water to a wineglass lowers the pitch. Given adding more water decreased the length of the column of air, this can't be the correct explanation (shorter column of are should increase the frequency). Moreover, I've done the same "experiment" with the wineglass submerged to the same depth as it was previously filled (ie., water is at the same height on the outside, as it was previously on the inside). The pitch was the same in both cases. I've also noted that the same volume of water at a higher temperature increases the pitch of the note. My question is what is the correct explanation for the change of pitch of a "singing" wineglass? (I think that is must be something to do with the damping effect of the water in direct contact with the glass. This makes sense given at a higher temp, the density of the water is lower, therefore the absorption of sound energy is less for the same height of water in contact with the glass. Less absorption, less change in frequency.)

ANSWER:
The reason is that it is not the air column but rather the glass which is resonating. Think of a mass on a spring: if you increase the mass (inertia) you decrease the frequency and I think that is what you are doing by adding water, increasing inertia against vibration. In that light, it is not surprising that you get the same frequency whether the water is inside or outside the glass (although I would not expect them to be precisely the same). The temperature effect may simply be that you are changing the elasticity (spring constant) of the glass by changing the temperature; try heating the glass without adding water.

QUESTION:
Since the speed of light is a finite number why would it take an infinite amount of energy for a spacecraft to trave at the speed of light? *i understand that the faster you go the more massive you become, but you cannot be infinitely massive to reach a finite speed. It doesn't make sense to me. Maybe Infinite mass and infinite energy should be replaced by "unknown"?

ANSWER:
You are thinking about this all wrong. What you have to do, once you understand relativity, is to compute the total amount of work which you must do in order to acquire a speed v for a particle whose mass is m. In classical physics this turns out to be mv²/2, but classical physics is only approximately true and becomes invalid for high speeds. The correct expression for the kinetic energy, the work you do, is mc²/(1-v²/c²)^1/2-mc². (Here m is the mass of the object at rest.) This expression may be shown to reduce to mv²/2 for v much smaller than c but clearly becomes infinite for v=c. Thus, to accelerate a particle to the speed of light requires an infinite amount of work (energy).

QUESTION:
I am a 16 year old student currently enrolled in Physics at my high school. I was given an extra credit assignment in which I have to figure out all the steps to convert meters per second to miles per hour. I need to know every single step in completing the conversion. I have done research, and have found nothing that has helped me out. Thank you for your time.

ANSWER:
The trick to unit conversion is to repeatedly multiply by 1.0 (we can always do that, right?) until the units are what we want. Since I will not do your homework for you (it violates the groundrules of this site!), I will work out an analogous problem. Suppose that I want to convert a pressure expressed in pounds per square inch (psi) to the more "scientific" expression of newtons per square meter. For a concrete example, let's do 14.7 psi which is about atmospheric pressure:

14.7 (lb/in²)x(1 in/ 2.54 cm)²x(100 cm/1 m)²x(1 N/.225 lb)=1.01x10⁵ N/m².

QUESTION:
How much helium does it take to fill a standard balloon ? Is there a way to measure helium ?

ANSWER:
First your second question: there is certainly a way to measure helium, or anything for that matter. One way is to simply measure its mass (in grams or kilograms). Another, often more useful way, is to measure its molecular weight in moles where you have one mole unit for each molecular weight unit. For example, atomic hydrogen has molecular weight of 1 but it normally occurs as the H₂ molecule, which is two hydrogen atoms bound together so its molecular weight is 2. Hence, one mole of H₂ gas has a mass of 2 grams. Helium has a molecular weight of 4, so one mole of hydrogen has a mass of 4 grams. The reason that a mole is useful is that 1 mole of any material has the same number of molecules, about 6 x 10²³ which is called Avagadro's number. Of course once you know Avagadro's number, you could also measure the amount of helium by stating the total number of atoms in the sample.

Now, to your first question: I do not think there is such a thing as a "standard" balloon, and it depends on how much you blow it up. Suppose we have a balloon which has a volume of about one gallon which would be about 4 liters which is V=4 x 10^-3 m³. The pressure would have to be bigger than atmospheric, so let's say that it is about 2 times atmospheric pressure which would be about P=2 x 10⁵ N/m². Suppose that the temperature is room temperature, about 20⁰C which is, in absolute temperature (kelvin) about T=273⁰K. Now there is a very useful equation called the ideal gas law, which works extremely well for most gasses at normal conditions which is PV=nRT where n is the number of moles of the gas and R is called the universal gas constant and has a value of about 8.3 for the units of things I have used here. So, n=PV/RT=0.35 moles. So, since a mole is 4 grams, the mass is about 1.4 grams. This answers your question. By the way, 0.35 moles is about 2.1 x 10²³ atoms.

QUESTION:
I was just wondering, could the principle of superposition of waves be used to muffle or even silence a noise projecting from a sound source? So, perhaps if a source of sound was project a particular frequency, and i places another source of the same frequency and ampilitude in another position, say half a wavelength behind, could the original noise be silenced?

ANSWER:
Yes. In fact, that is how noise-cancelling headphones work--the external sounds are captured by a microphone, flipped, and added back to the incoming sounds. Then you hear only (almost) the sounds being sent to the headphones, music, talk, etc. Pilots often use this device so that the hear only other crew members, ground controllers, etc. The answer to your second question is also yes but you must also take care that the two speakers are in phase. This kind of destructive interference is responsible for "dead spots" in concert halls.

QUESTION:
Why is heavy water (D₂O) used in moderators of Nuclear Power Plants instead of normal water (H₂O)? If heavy water (D₂O) absorbs and slows down the neutrons emmited in fission what happens to it?

ANSWER:
The purpose of a moderator is to slow neutrons down so that they will be more probable to be absorbed by a fuel nucleus (e.g. uranium) and cause a new fission. And each new fission becomes the source of more neutrons, but they are fast and the moderator slows them down. If you use something like lead as a moderator, it would work poorly because the scattered neutrons would have almost no loss in speed (think of bb's bouncing off bowling balls). But, if you use something light, like hydrogen, then you are bouncing neutrons off something about the same mass which will quickly slow them down (think of a head-on collision between two billiard balls where the cue ball stops dead). So, hydrogen gas or liquid would be the best moderator, but hydrogen is very explosive, so we use something rich in hydrogen, water. But the problem is that a single proton can easily combine with a slow neutron (to create a deuteron) but that removes the neutron which we want to use to cause more fissions. The purpose of the moderator is not to remove neutrons, so we try the next lightest atom, deuterium, which is chemically identical to hydrogen but has a mass about twice as big. It is not quite such a good moderator, but it has a very small probability of absorbing neutrons. In the event that it does absorb a neutron, it becomes hydrogen with one proton and two neutrons and is called tritium. Tritium is radioactive and harmful to the environment.

QUESTION:
I've heard of this experiment: Two parallel mirrors are set up and a laser is fired perpendicularly between them. It is then possible to view the beam of laser light (maybe with some dust or smoke between the mirrors) falling towards the earth with an acceleration of -9.8 m/s/s. Is this possible? If so, has this ever been performed?

ANSWER:
It is true that light will fall with an acceleration of 9.8 m/s²(but retaining a constant speed, that is the vertical component of the velocity would increase), so in principle your device would work. But, think about the scale of things. If the mirrors were 3 m apart, it would take 10^-8 s for the light to go from one to the other. In this time the light would "fall" 9.8 x (10^-8)²/2 m which is about 5 x 10^-15 m, about the size of a nucleus! I reckon (gt²/2) that it would take about a hundredth of a second to fall 1 mm, right? But in this time, light travels 3 x 10⁸ x 10^-2 = 3,000,000 m, a million reflections in our device. But no real mirror is completely reflective; an amazingly good mirror would be 99.9% reflective, but a million reflections would leave you with about 10^-435 (.999^1,000,000) of the initial intensity! Clearly, this seems to be an impossible experiment and I very much doubt that any variation of it has been done.

QUESTION:
Would a type of nuclear reaction take place if a proton entered a specific atom at a certain rate, or if a neutron entered at a certain rate? Is this considered the splitting of an atom or just one atom becomming another atom? Would there be any kind of an explosion? What happens to the gluons in each case?

ANSWER:
Just about anything which is energetically possible can happen. Take some examples: a proton could be absorbed by the nucleus and stay there creating the next element in the periodic table; it could knock out a proton while passing through creating the previous element in the periodic table; it could knock out a neutron creating the next lightest isotope; the struck nucleus could split into two heavy, but much lighter than the target, nuclei (called fission); and just about anything you can think of, as long as there is enough energy carried in by the proton to do it. "Splitting of an atom" is a qualitative term but usually refers to fission. Neutrons are better for causing nuclear reactions since slow neutrons can interact easily with the nuclei whereas, since the proton and the nucleus both have positive charge so it takes a much faster proton to get close enough to the nucleus to interact with it (the nuclear force is very short-ranged). Anything you can do which involves a single atom will not cause what you would call an "explosion", but if you make many things happen at once so that a large number of nuclei participate, you could get something observable on a macroscopic scale. That is how an atomic bomb works (or a reactor): one neutron causes a fission, but a fission releases several other neutrons and some of those will create new fissions, and so on and so on. There is no reason that a third grader needs to be thinking about gluons!

QUESTION:
Assume two identical objects A & B, with a rest mass of m, moving relative to each other at a velocity V. The question is this: what is the energy equivalent of A? According to relativity theory, the energy of A = mc², where I assume, m is the mass of the object from the point of view of an observer in the same frame of reference as A. BUT, also according to relativity theory, when an object moves, its mass increases, which we will call M [capital M). So the the energy of A, since it is moving relative to B, = Mc². There then appears to be a paradox: the energy equivalent of mass A is two different amounts, depending on whether the observer is in the frame of reference of A (stationary) or B (who sees A moving at velocity V). The object itself has no way of knowing whether it is moving, so it seems there should be only one correct answer. Is this a paradox?

ANSWER:
You do not have to do special relativity to answer this question. Energy is a relative thing, its absolute value has no meaning; all that matters is the amount by which it changes when things happen. Take a book which sits on the table (and I am doing this nonrelativistically). If I choose the position of the table top as the level of zero gravitational potential energy, then this book has zero energy. If I run past it, however, it moves relative to me with some speed v and therefore has energy of mv²/2 (kinetic energy). If I raise it some distance above the table top it now has some amount of potential energy. It is always the same book but with just about any amount of energy I like. No paradox. In relativity, mc²(with m the mass of the object at rest is called the restmass energy). If an object moves its energy is Mc² (with M the mass it has when moving). The kinetic energy is by definition Mc²-mc² and this will be approximately mv²/2 if v is very small compared to c.

QUESTION:
V=IR
Either increase R or I Voltage(V) will increase
Which of the two we are increasing in a step up transformer while increasing the voltage as far as I know Current (I) decreases while stepping up the voltage than is it the R that we are increasing?

ANSWER:
A transformer is not an "Ohmic device" and so Ohm's law is not true. The reason that I decreases when the voltage increases is that energy must be conserved and the power, the rate at which energy is consumed (or delivered) is P=IV. So P_input=P_output.

QUESTION:
In Global Warming, I understand there is a shifting of visible energy to longer wavelengths by the land mass and oceans which then radiates this energy to the greenhouse gases in the atmosphere which in turn re-radiates the energy back to earth. 1. What accounts for the shifting of the energy from the shorter 400- 700 nm range) to the longer IR & ‘heat" wavelengths? Is it analogous to Fluorescence spectral shifting phenomena? 2. In a theoretical situation, if only pure visible wavelength energy fell on a perfect black body, would the black body absorb all of this energy, raise its temperature and reradiate it (at longer wavelengths) outward?

ANSWER:
Question number 1: Matter absorbs electromagnetic energy and the result is that it heats up; a hot object radiates energy but mostly in the infrared region.

Question number 2: Yes, except that the radiated spectrum would depend on the final temperature of the black body. I.e., if the black body were originally very hot such that most of its energy was at short wavelengths, the final spectrum would be hotter and peak at even shorter wavelengths.

QUESTION:
How does a ballon gain positive charge?

ANSWER:
What normally happens, since it is negatively charged electrons which can be moved around most easily in normal matter, is that an object becomes positively charged by losing electrons.

QUESTION:
if you shot a bullet directly up, when it came back down would its speed be the same as when it left the gun or does terminal velocity prevent that.

ANSWER:
If there were no air friction, the speed would be the same. But there is significant air friction which takes kinetic energy away from the bullet, so it is going more slowly when it hits the ground. Incidentally, because the earth is rotating, the bullet would not hit precisely at the point from where it was fired straight up.

QUESTION:
So we move with the earth through space as it both orbits the sun and rotates on it's axis. Now the closer we get to the speed of light the slower time passes for us. Does this mean even when stationary on the ground our perception of the passage of time is altered because the earth is moving fairly fast through space? If so how much faster do we move through time then someone not moving along with the earth or anything else. If not why?

ANSWER:
In your own frame, time will progress at a perfectly normal rate. It is only the rate of your clocks relative to clocks in motion with respect to you which run slower. See my discussion of the twin paradox in an earlier question. Incidentally, the motion of the earth is far too slow for any easily measurable effects to be observed since the earth's speed relative to any other clock you are likely to compare it to is very small compared to the speed of light.

QUESTION:
Does the Heisenberg Uncertainty Principle say (a) that particles have a definate position and momentum, but we are incapable of ever knowing them both simultaneously or (b) that particles do not have a definate position and momentum at all?

ANSWER:
Technically, one may know one (position or momentum) with perfect precision if we are totally ignorant of the other. However, we can never be totally ignorant of either in practice (for example, surely the particle in question is somewhere in the universe). So, both your (a) and your (b) are correct, but (b) cannot be by itself a statement of the principle because the degree to which we can know one is determined by the degree to which we know the other.

QUESTION:
What is the shortest wavelength (I assume in the gamma range) that has ever been experimentally observed.

ANSWER:
The most energetic photon which I could find reference to was a cosmic ray of energy 3.2 x 10²⁰ eV (observed in 2004 by the Fly's Eye Detector). Since E=hf and f=c/l, l=ch/E=(3 x 10⁸ m/s)(4.1 x 10^-15 eV s)/(3.2 x 10²⁰ eV)=3.8 x 10^-27m. Here, h is Planck's constant and c is the speed of light.

QUESTION:
Can you tell me if anyone has studied the conection between gravity waves and bremmstralung? For example if a charged mass were orbiting a significantly larger mass it would emit both gravitational waves, (at least according to general relativity) and electromagnetic waves. Has anyone studied at least the theoretical model of this? How would the energy radiated by one field compare to the other, both separately and simultaneously?Would they radiate less energy when simultaneous?

ANSWER:
Electromagnetism and General Relativity are separate theories. In the case you suggest, both gravity waves and electromagnetic waves would be emitted and would have nothing to do with each other as far as we know (although some have suggested that general relativity may have effects on electromagnetism). Both phenomena have been fully explored theoretically. I should of course include a disclaimer here: nobody has ever directly observed a gravity wave but some physicists are trying very hard.

QUESTION:
can matter at absolute zero be seen ? could dark matter be this ? i mean, if matter was at absoulte zero, is it possible it still has mass but we cannot see it ?

ANSWER:
Matter exactly at absolute zero cannot be because of several laws of physics. However, let's suppose that there were a chunk of matter at absolute zero. Could it be "seen", that is detected? Well, if it were just sitting there by itself in totally empty space we could not "see" it but then we could not see a nearby piece of matter at any temperature. If light were to strike it, I do not see why the light would not be either reflected or absorbed, and in either case we could detect that so we could "see" it.

QUESTION:
Why does light travel in a srtaright line and sound don't?

ANSWER:
Light does not travel in a straight line necessarily any more than sound does. The simplest example is a mirror which clearly changes the direction of light. Light is also bent by entering a different medium which is how lenses work. Light is also bent (ever so slightly) by gravity. Light is also bend by diffraction (for example, you can never make a perfectly sharp shadow of something because light bends as it passes the edges.

QUESTION:
I have a problem with the standard explanation of atmospheric pressure as beeing caused by the weight of the air lying above. If i have a hermetic closed bowl of glass (or something else), so there is no way forces can be transmitted from the inside to the outside, how am I to explain the pressure in the bowl as caused by the weight of the air above ?

ANSWER:
What matters is the environment when you close the bowl. If you simply close it in atmospheric pressure, there will be atmospheric pressure inside it. If you were then to pump the atmosphere away, the pressure inside the bowl would still be the same. If you were to pump more air into the bowl, the pressure would increase and pumping it out would decrease the pressure. These subsequent changes would be due to you, not the atmosphere.

QUESTION:
I'm not quite sure that I understand the theory of relativity. Is it true that light NEVER slows down; that instead, time is slowing down? (such that the m/s speed of light is the same as always, but a second becomes longer)

ANSWER:
The speed of light in a vacuum is always the same, regardless of the motion of the source or the observer. As a consequence of this, moving clocks run slowly (which is called "time dilation"). Light does move more slowly in a medium (say glass, air, water,...) which is responsible for optical instruments like eyeglasses, cameras, telescopes, etc. working.

QUESTION:
If the half life period for say Uranium is constant then it should be that every atom of particular mass of Uranium degrade simultaneously and say after the half life for one atom whole number of atoms in that mass should get degraded and hence no more remians mass of Uranium but some thing else. Is it so?

ANSWER:
What half life means is that at that time half the number of original atoms will be converted into something else. It is useful only for a very large number of atoms because radioactive decay is a statistical process and you cannot know when any given nucleus will decay, only what the probability for decay is. After many half lives almost all the uranium will be gone.

QUESTION:
What generates more energy? A explosion or an implosion? Also, which takes more energy to create?

ANSWER:
This question has no meaning in physics. In the overall picture, energy is conserved in any case. Take a conventional bomb (TNT): Energy is chemically released from the explosive TNT and reappears as light, heat, sound, and the kinetic energy of the fragments. The same is true for the case of implosion: Chemistry provides energy but there are no fragments flying out so more of the original energy ends up as heat, light, and sound than in the case of the explosion. In all cases, something provides a certain amount of energy and it shows up somewhere else.

QUESTION:
How does beta particle radiation produce heat energy? Does it do it by merely striking a nucleus and increasing the movement of the atom? I have never read material that explains that a beta particle strikes a nucleus and increases the vibration or movement of the atom itself. Or is the heat energy produced when the beta particle knocks an electron off of an atom and then the atom later picks up another electron and so produces heat in an indirect fashion (an exothermic reaction where the atom picks up an electron)? To me that would be the conversion of kinetic energy of the beta particle to heat energy.

ANSWER:
The beta particle is just an electron (or positron) and loses its energy almost entirely by interacting with the atomic electrons, not the nuclei. Atoms become excited or ionize, then deexcite and emit electromagnetic radiation (light, x-rays, etc.) which gets reabsorbed and eventually ends up as heat, increased kinetic energy of the absorber atoms.

QUESTION:
Using the electron flow model is it correct to assume that flow is from the earth to the generator?Is it correct to assume that the earth is negative in regards to the generator?Or is the generator more negative than ground?

ANSWER:
One of the most important points about electric potential is that its zero is arbitrary. We usually call the point where we define zero potential to be "ground" or "earth", but that point need not be the actual physical earth. The one thing which you may be certain of is that electrons will always flow from low potential to high potential. Thus, if you call the earth zero potential and if your generator is at +5 volts, then electrons will flow to the generator. On the other hand, if the generator happens to be at -5 volts, electrons will flow from the generator.

QUESTION:
I am fascinated by magnetism, most likely because I do not understand its limits. I recently read somewhere that it has been determined that gravity "flows" at the speed of light (i.e. if the sun were to inexplicably vanish, it would still take eight minutes for it to disappear from the sky and for the earth to drift from it's orbit). Does a magnetic field behave similarly, or is it instantaneous in effect?

ANSWER:
Electromagnetic fields all propogate at the speed of light. Thus, if you created a magnet on the sun, it would take 8 minutes before you saw the magnetic field on the earth.

QUESTION:
What is equivalent of 250 rpm in x gravity?

ANSWER:
I presume that you want to know how many g's of acceleration 250 rpm is. Well, you have not given me enough information because the acceleration depends on the radius of the circle the object is moving in. The acceleration of an object with speed v moving in a circle of radius R is v²/R. So the acceleration of an moving at 250 rpm which is 250/60 rps=4.17 s^-1. So, the speed would be v=2pR x 4.17=26.2R m/s. So, the acceleration would be a=(26.2R)²/R=685R with the answer being in m/s² if R is expressed in m. The acceleration due to gravity is 9.8 m/s², so a=685R/9.8=69.9R in g's. So, for example if R=0.5 m, a=35 g's.

QUESTION:
If e=mc2 than what does happen when --e=-mc2. Will time stand still? If you go backward and time is always trying to catch up would you not be caught in in a loop.

ANSWER:
Sorry, this question doesn't really make any sense. You might want to study some about Dirac who postulated a filled "negative energy sea". When a particle is elevated from this sea to the realm of positive energy it leaves a hole behind. This hole is an antiparticle.

Note to this questioner: I cannot answer your questions about a career in physics because the email address you gave me does not work. Also questions of this sort I will often answer but not here because this site should be reserved for physics questions.

QUESTION:
During the past several months, I have been working my way thru an "Elementary Modern Physics" by Weidner & Sells (circa 1962). For the most part, I been able to handle the majority of the problems, but have slammed into several that I can't breakdown. One of these is as follows: "What is the mimimum speed of a particle such that its kinetic energy can be written as its total energy E, and therefore as pc, with an error in total energy no greater than 1%?" This implies that this is in the extreme region where E~pc (momentum) & this confirmed by the solution below. I have not been able to set-up the equation required to yeild the solution = 0.9995c. What seemed routine at first has become something else. At least one author said to ignore the rest mass energy in the extreme region, but when I do that I get E=pc or mc^2 = mvc , hence v=c & this not correct. There has to be some small factor (~1 in 2,000) to achieve the text's solution. However, when I write E = Eo + KE & try to work it thru I get "bogged down" in the algerba with (1-beta^2)^0.5 factor. I'm about out of bullets & to the point of frustration. It's clear to me that I have missed something in my understanding of the set-up of the initial equation. I am asking for any coaching & direction you or perhaps a graduate student might have. I'm also working thru a similar one that has a different twist ......."it asks what's the maximum speed a particle can move so that its KE can be written as 1/2 Mo*v^2?" If I can solve the one above then I think this one will fall out.

ANSWER:
A detailed answer may be read here.

FOLLOWUP QUESTIONS:

You indicated that m always refers to rest mass (Mo), and I assume that the momentum (p) in these equations refers to the classical momentum p=Mo*v,

otherwise the terms would not cancel out? I did not see any use of the gamma term. Am I correct?

also, since you knew that this was "slow speed relative to c "........... is this the reason to use classical in this application?

ANSWERS:

No, p is relativistic momentum, mu/sqrt(1-u²/c²) where u is particle speed.

The gamma is in p. I view linear momentum as the thing that is redefined in relativistic mechanics, not mass. It must be redefined to have momentum conserved in an isolated system.

What I know is that in the limit of small u special relativity must reduce to Newtonian mechanics. Hence, we must have T=.5mv² for u<<c or equivalently pc<<mc².

The email address you used to send your question does not accept my email to you!

QUESTION:
If there was a circular race track, and it had three lanes; one car on the inside lane and one car on the outside lane. Would the centrifugal (or is it centripetal) force of the cars be equal if it takes the same time for them to complete a lap. Because while the one on the outside lane is traveling faster; it has a softer angle. The one in the inside lane is travelling slower but with a sharper angle. I thought of this when tryingt o go to sleep in the car and feeling the centrifugal force when going round bends.

ANSWER:
First let's get straight the difference between centripetal and centrifugal forces: an object moving with speed v in a circle of radius R will have an acceleration (called centripetal acceleration) v²/R. Because of Newton's second law, a force must cause this acceleration, so F=mv²/R. If you are riding in a car and leaning on the outer door, the door pushes on you with with this force, called the centripetal force. Because of this real push, you have the perception of being pushed against the door with a force equal to the centripetal force; you are not really being pushed into the door, you just feel that way. In physics this is what we call a "fictitious force" and, in this case it is called the centrifugal force. Another example is when the car is accelerating you feel that you are being pushed back into your seat but what is really happening is that the seat is pushing forward on you.

Now to your question: Since the speed v=2pR/T if the period is T, the centrifugal and centripetal forces (mv²/R) will not be the same for both cars because v² is proportional to R². The ratio of the forces would be F_out/F_in=R_out/R_in, that is the outer track would have larger force.

QUESTION:
What are colours, does it have any physical mass?

ANSWER:
Color is a qualitative way to describe the differences between wavelengths of visible light as perceived by our eyes and brain. It is not an object, so to ask if it has mass is meaningless. Photons, from which light is composed, have energy but no mass.

QUESTION:
if there is an object with zero inertia, and there are enormous forces of the same strength pulling at it from all directions, so the all cancel out. will it take some effort to move this object? or will the object be like.. nothing?

ANSWER:
Dynamically, an object with zero net force on it (as you describe) is identical to one with no forces on it, so we need only ask ourselves what happens when we exert a force on an object with zero mass. It will experience infinite acceleration because a=F/m; by the same token, an object with zero mass can have an acceleration when there is no net force on it. This all sounds quite bizarre, but keep in mind that there is nothing with zero mass (photons do not count because classical mechanics does not apply to them.) We often talk about objects with zero mass in elementary physics problems, for example "...the pulley is massless and frictionless" but these should be understood as approximations, that is the mass of the pulley is very small compared to other masses in the problem. A force acting on an object with very small force will result in a very large acceleration.

QUESTION:
Do photons have mass? In one of your answers you say no. My penquin dictionary of science says, no mass. However, in the September 2006 issue of ASTRONOMY, the article, ASK ASTRO page 63. It is stated that the photon's mass is less than 10(-50)kilograms. Or 14 orders of magnitude smaller than a neutrino. Very low mass, yes, but there is mass. Is a photon massless?

ANSWER:
When we say that photons have no mass, we mean that every measurement we have ever made is consistent with their having no mass. However, it is often of interest to test the limits of our knowledge: how accurately do we know that the photon is massless? Most likely the article you were reading put an upper limit on what the mass of a photon could be based on experiments, 10^-50 kg.

QUESTION:
I was wondering whether or not one could accelerate a mass of about 1 kilogram in a large particle accelerator to nearly the speed of light. If this is possible, how fast would the mass go, how large would the particle acclerator have to be, and how much energy would be needed to acclerate the mass? Also, what type of energy is released when two particles or in this case one kilogram objects collide or what percent would be light and what percent would be heat.

ANSWER:
It is not feasible to accelerate a 1 kg mass in a particle accelerator because the 1 kg mass is not charged. Even if you caused it to become highly charged, the force of gravity on it (its own weight) would be larger than any electrostatic force you could exert on it so the accelerator would not work. The speed, if close to the speed of light as you stipulate, would be about 3x10⁸ m/s. The energy would be about 10²⁶ times larger than the energy of a proton having the same speed. The energy of 1 kg going 99% the speed of light would be about 6.4x10²⁰ Joules. If you accelerated it to this energy over the time of one year, you would have to continuously supply over the year about 20,000 Gigawatts of power! There is no way to know exactly what will happen when two objects collide.

QUESTION:
Do electrons contain photons? Electrons emit photons when elevated to higher energy level. E=mc². Photons are massless but are energy. Does not all energy have mass? What happens to photons in a beam of light in a dark room when the beam is switched off?

ANSWER:
We do not think of electrons as "containing" photons although they are thought to be surrounded by a cloud of virtual photons popping into and out of existence. The emission of photons from excited atoms is due to a creation of a photon, not the "release" of one. Not all energy has mass, the photon being the perfect example. Every object has a total energy part of which is due to its mass and part of which is due to its motion (kinetic energy). Photons get absorbed by the walls in a dark room.

In future, please note that one of the groundrules for this site is to ask single, well-focused questions.

QUESTION:
Could the comparison of an atom and a solar system exist with the current understanding of nano science. I.e. do electrons orbit the nucleus of an atom in relation with a nuclei's weight or mass? Do the nucleus' of atoms emit light?

ANSWER:
No. Gravity is not the force which holds the electrons in their orbit. It is the electrostatic force (the attraction between the negatively charged electrons and positively charged nucleus) which does it. Gravitational forces in an atom are entirely negligible compared to the electrostatic force. Mass, however, is not irrelevant, however. The mass of an electron is very small compared to the mass of the nucleus, so the nucleus, for all intents and purposes, remains fixed as the electrons orbit. If the mass of an electron and a proton in a hydrogen atom were equal, the two would orbit about a point halfway between them, much like a binary star.

Regarding your second question, yes a nucleus emits "light" but not light you could see. When an atom emits light it is often within the visible spectrum. The electromagnetic (called gamma rays) waves emitted from nuclei are much more energetic and thus of a far shorter wavelength than your eye can see.

QUESTION:
I'm a photographer. I take photos that take advantage of what I call 'gravitational lensing'. I set up a black rod between the camera and the subject. If I get just the right 'focus' setting on the camera I can get the the background and the rods out of focus but the areas of overlap seem to come into focus. My guess is that, when the photons travel from the background to the camera they are pulled closer together by the mass of the rod and therefor they appear in more focus. The best examples are images #0518a and #0512 at http://www.morgan-anderson.com/artwork/2005Works.html I've been working with this phenomenon for a couple years and, while I have a cursory understanding of it, I'd like to know for certain what I'm doing. So My question is: what is the physics behind this?

ANSWER:
Let's first dispense with what the explanation cannot be. Since the gravitational pull on light is so incredibly weak, there is no possibility that the mass of the rod can have any observable effect on light; deflection of light passing close to the sun, with huge mass, is extremely small and difficult to observe. For this reason, you should probably not call, even whimsically, what you are seeing "gravitational lensing" because, whatever it is, it certainly has nothing to do with gravity. What it most looks like is diffraction. When you put an obstacle in the way of light, the light which comes from either side of the object interferes and results in light and dark fringes. What worries me about this explanation, however, is that diffraction is usually hard to see except for monochromatic light and what you see seems to come from the whole spectrum. So maybe there is some explanation from geometrical optics (optics which does not depend on the wave nature of light), but I would need more information to make any further guess: how thick are the rods, is there more than one of them, where are they relative to the camera, where is the focus of the camera when you see these effects? Being a photographer, you should probably take it upon yourself to learn about diffraction.

QUESTION:
I teach Science in Oconee County, Georgia. In class one day we were discussing the Northern Lights and they are "cosmic radiation" that is being burned up in our atmosphere at the poles due to the high concentration of magetism from the earth's magnetic field. I had two questions, wondering if you guys might be able to help me answer the questions:

I wanted to make sure I was correct in the cause for the northern and southern lights.

I had a student ask, why we couldn't use large magnets or even the magnetic north/south pole to stop large scale radiation type attacks, ie. whether it be a nuclear war, an atomic bomb, or even to help clean up something like the leak at the Russian nuclear plant?

ANSWER:
Referring to northern lights as "radiation...being burned up" is inaccurate. Here is a brief explanation: There is a constant stream of electrons and protons which come from the sun called the "solar wind". (During times of intense sunspot activity the intensity of these particles increases.) If the earth did not have a magnetic field, these particles would simply plow through the earth's atmosphere (ionizing and exciting atoms as they went) and then hit the ground where they would lose all their energy. But, because the earth is like a giant bar magnet, these incoming charged particles get deflected and their tendency, because of the nature of the magnetic force, is to spiral around the magnetic field lines toward the poles. Hence, there is a concentration of these charged particles around the poles (which is why the aurora phenomena are usually very far north or south) and as they follow the field lines down, they strike the upper atmosphere. When these energetic particles hit the air, they ionize (knock off an electron or two) the atoms along the way and when these ions recombine with electrons, light is emmitted--hence the "lights" part of the phenomenon. So, you see, it is not really a case of radiation being "cleaned up" at all. The cases you refer to are nuclear radiation and there the most damaging radiation is usually gamma radiation which is very energetic electromagnetic radiation (like x-rays but even more energetic); since gamma rays have no electric charge, they are totally unaffected by magnetic fields.

QUESTION:
Does the refractive index of salt solution change with its concerntration? If yes, what is the best way to determine it?

ANSWER:
I can't imagine that it would not vary. There are numerous ways to measure index of refraction, too many to enumerate here. Generally, you need to have a setup which allows you to measure the angle of refraction for a known incident angle and use Snell's law. Another way to do it is to measure the critical angle of total internal reflection.

QUESTION:
I know that we see the colors of the visible spectrum from the interaction of the different frequencies of visible light as seen from our eye and our brain. In other words, there is no intrinsic "color" property for a specific frequency of light. My question is this. If our eyes were sensitive to say the ultraviolet region of the EM spectrum instead of the visible region and the things around in our environment (i.e. trees, concrete, buildings) reflected and absorbed the uv light like they do visible light, would our eyes discern different "colors" for different frequencies within the uv region? In other words, is there anything special about the visible section of the spectrum or is it simply that our eyes were made to see this region?

ANSWER:
The idea of color is, as I see it, a purely subjective thing. In fact, how do I even know that what you see as green is the same as I see as green? The only thing, from a physics perspective, which matters is that you and I are able to distinguish between different wavelengths of the spectrum to which our eyes are sensitive (assuming that neither of us is color blind). Also, it is necessary from a scientific point of view, that our observations be repeatable, that is green, once I have learned it, will never look red to me. Animals have a variety of color sensitivity which you can learn about on the web by googling "color vision in animals". Insects, which have an entirely different eye structure from other animals, use primarily ultraviolet light since the resolution of their eye is maximized for very short wavelengths. There is no simple answer to your question since it depends on the detailed structure of your eye (rods, cones, etc.), but there is no reason why, had our eyes evolved like the insects to see ultraviolet light, we could not, in principle, distinguish between different wavelengths of ultraviolet light.

QUESTION:
Usually when I get bored, I spin my chair. First I take a spin with my legs in. When I strech my legs out, the speed decreases, which is abvious because of the laws of the centrifugal force. The weird think, though, is when I retract my legs again, the speed INcreases after it has decreased. I asked my scince teacher about this conundrum, and her suggestion was that perhaps I retracted my feet fast enough to give my spin energy enough to spin faster. To me that just doesn't seem right.

ANSWER:
First of all, there is no such thing as "the laws of the centrifugal force", so though it may be obvious to you that you slow down, it should not be! What you are experiencing here is conservation of angular momentum. Angular momentum is the product of the angular velocity (for example, the number of revolutions per second) and the moment of inertia the object has relative to the axis about which it is rotating. Moment of inertia is essentially a measure of how far away, on average, the mass of the object is from the axis of rotation. So, when your legs are in your moment of inertia is smaller than when your legs are out. The angular momentum of an object remains constant (is conserved) if there are no external torques on the system. You and the chair spinning can be approximated as having no torque, although there is some due to friction which will eventually, as you know, cause your angular momentum to vanish (because you stop spinning). But, over the short term, your angular momentum stays about the same, so if you put your legs out your angular velocity must decrease and if you pull them in, it must increase. This is the same principle dancers and skaters use to increase their spin rate by pulling in their arms.

QUESTION:
Classical physics texts all have common problems where a horizontal force acts on a triangular wedge with a rectangular block (of smaller mass) sitting on the wedge's incline (the net force accelerates both masses). Some problems have the surface between wedge & block as frictionless & some don't. However, in all the problems I've seen, the surface between the wedge & horizontal surface supporting it are frictionless. Is this done to avoid the so called 3 body problem, or is there another reason? Just curious.

ANSWER:
I am a stickler on the way you state problems like this, so first let me reprimand (!) you for a conceptual problem: The force pushes on the block and not the wedge and therefore the force does not accelerate the wedge, the block (which is touching it) does. The only thing you must make sure of is that there are not more unknowns than equations. If you add friction to the table surface, you have not added an unknown since it is proportional to the normal force between the wedge and the table. So, if you can do the frictionless problem you can do the one with friction. It has nothing to do with the 3-body problem in which you cannot write an analytical solution to the motion of three bodies mutually interacting via central forces (like a planet with two moons).

QUESTION:
I am trying to find the launch angle required for a ball to clear the net of a tennis game. For example if I want to perform a drop shot no matter where I stand in the court, I want to place the ball so that it lands close to the net at the opposite side while making sure that it clears the net. I manage to work out the formula for calculating the initial start velocity required for the ball to reach the destination but I can't quite figure out the formula required to clear the net. There is one in-efficient solution I came up with, that is that I can just check if it manage to clear the net, and if the ball failed to clear the net I can increase the launch angle... but there got to be a better solution for this.

ANSWER:
You seem to have too many unknowns as far as I can figure out what you want to do. Here is what you can do: you can choose a particular distance from the net, an initial velocity, and an unknown launch angle, and an initial height from the ground. Then, stipulating that the ball just clears the net, you should be able to solve for the angle. You will get two answers: one corresponds to a fairly low trajectory and one corresponds to a lob. The lob will hit closer to the net.

QUESTION:
In my readings about relativity, much is made of the equivalence of gravity from a mass, and acceleration due to thrust, such as a space ship either sitting at sea level on a planet vs. the same space ship accelerating at the equivalent rate in free space. In fact, these two situations are supposed to be indistinguishable by experimenter or experimenters within the space ship. However, wouldn't they be able to discern which by using two plumb-bobs, which in the case of being under thrust would be parallel to each other but at rest on a body of matter, would each point towards the center of mass of the body, and therefore make an angle (vanishingly small under realistic conditions, but this is a thought experiment, after all) to each other?

ANSWER:
You are right, you could distinguish between an accelerating frame and a nonuniform gravitational field, for example from a planet. The adea you allude to assumes the gravitational field to which you compare the accelerating frame is uniform.

QUESTION:
Many references define gyroscopic precession as "a phenomenon occurring in rotating bodies in which an applied force is manifested 90 degrees later in the direction of rotation from where the force was applied." This does not jibe with my understanding, which is that gyroscopic precession is the movement of a rotating body in a gravitational field, where the axel on the axis of rotation is secured at one end, and such axel sweeps out a cone. If my understanding is correct, what do we call the phenomenon described above? My old college physics text describes the phenomenon, and obviously mathematically models it (with vector cross-products), but does not name the phenomenon.

ANSWER:
Remember that Newton's second law for translational motion may be expressed as force equals the time rate of change of linear momentum. In rotational physics, the corresponding statement is torque equals time rate of change of angular momentum. Imagine a top spinning about an axis through its center of mass and in empty space. Its angular momentum is along this axis and, since there are no torques on the top, the spin axis stays fixed (no precession). For example, the angular momentum of the earth points along the axis and from south to north poles; the fact that this direction always points to the north star demonstrates that the angular momentum is constant (conserved). Now take the top and exert a torque on it (a spinning top, unless standing straight up, has a torque due to its own weight). The result, due to Newton's second law is that the angular momentum vector will not remain constant; the way it changes is to change its direction, hence precession. This is a simplified explanation; the top problem is one of the classic problems in classical mechanics to understand in all its gory detail. I hope this gives you a better qualitative understanding.

QUESTION:
If two rockets of the same weight were placed at the same height, and one was dropped in free fall and the other launched horizontally, wouldn't the one dropped hit the ground before the one flying would? (assume wind resistence is negligible)

ANSWER:
Yes, because I presume you mean by "launched" that its rocket is burning; in principle, it could keep going horizontally until it ran out of fuel. You are, I think, confusing this with the situation where it is projected horizontally but does not have a rocket engine. In this case, both hit the ground simultaneously.

QUESTION:
Is the statement correct: "Today the temperature is 40 degrees Celsius and yesterday it was 20 degrees Celsius so it is twice as hot today as it was yesterday"

ANSWER:
Although "as hot" is a qualitative statement, physicists would say certainly not. It is the Kelvin temperature which determines the energy content of something, and the Kelvin temperature is 273 degrees below the Celcius temperature. Thus the two temperatures would be 313^oK and 293^oK. Maybe you could say that 40^oK is twice as hot as 20^oK

QUESTION:
What is the angular momentum of the spin axis of an atomic nucleus? I have only heard about this in advanced physics. Is there any way one could reverse the spin axis of the angular momentum of an atom?

ANSWER:
The angular momentum of a nucleus is the sum of the angular momenta of its components. Each proton and each neutron has a spin (always 1/2 in appropriate units) and an angular momentum due to its orbital motion (always some integer in appropriate units); for each particle, its total angular momentum is the sum of these (always a half odd integer, i.e. 1/2, 3/2, 5/2...) If the nucleus has an even number of protons and of neutrons, the ground state angular momentum is always zero because it is energetically favorable for pairs to sum up to zero angular momentum. Only nuclei with odd numbers of particles or with an odd number of protons and neutrons have ground state angular momenta. The total angular momentum of a nucleus is usually referred to as its spin. To "reverse" the spin, you just need to flip the direction of the spin vector. So you should think of taking a spinning object and pointing its spin axis in the opposite direction, not stopping and reversing it; the effect is the same.

QUESTION:
Does everything in the universe rotate in the same direction?

ANSWER:
No. However, most things in the solar system do; if viewed from the north star, most objects in the solar system rotate counterclockwise.

QUESTION:
Lets say you had two rocket ships docked at a space station. They decided to leave the space station at the exact same time in completely opposite directions at 99% the speed of light. Both rockets traveled for one year (relative to the rockets time) and then at the exact same time reversed their directions and went back to the space station. The space station has now "aged"... thousands of years from when they left. Have the two rockets aged at the same rate? Would they each only be two years older compared to each other then when they left? Would the same apply if they traveled next to each or perpendicular to each others direction? How does special relativity (I think that is what it's called) effect these ships since you cannot say that one ship is moving 198% the speed of light compared to another ship which may be concided stationary.

ANSWER:
I have earlier answered just about the same question.

QUESTION:
"energy is matter, and matter is energy" Is this statement true?

ANSWER:
Matter is, indeed, a form of energy. This is the famous E=mc² relation of special relativity. I do not think most physicists would say that energy is a form of matter, however. That would sort of be like saying "horses are animals and animals are horses"!

QUESTION:
Determine the distance to which the painter of weight "w" can climb without causing the ladder to slip at its lower end. The top of the 15kg ladder has a small roller and at the bottom of the ladder the coefficinet of static friction is 0.25. The ladder is 1.5m away from the bottom of the side wall. I have drawn the free body diagram and realise that we need to be in equilibrium, my problem is the last step, How do I use this information to find the weight of the painter and how far from the wall it is?

ANSWER:
Although you do not specify it, I presume that you know the length of the ladder. Your solution should have three equations: one from setting the sum of the torques to zero and two from setting the sum of the forces (x and y components) to zero. Thus you may find three unknowns. You do not know the weight, the position of the painter, the normal forces of the wall and floor on the ladder; the frictional force by the floor, may be espressed in terms of the others since f=mN_floor. Seems to me that you have 4 unknowns and therefore cannot solve the problem.

QUESTION:
can thermal expansion be stopped

ANSWER:
Of course, you just have to push on the ends. This is analogous to containing a gas in a tin can and heat it up; it wants to expand but cannot because the volume is constrained so the pressure increases instead.

QUESTION:
I know that when I look at a flourescent bulb through a diffraction grating, I see emission lines, but why, when I look at a hot wire filament type bulb through a diffraction grating, do I not see the absorbtion lines of our own atmosphere between the wire and the grating? Why do I see a complete spectrum?

ANSWER:
Absorbtion is a relatively low probablilty event and there is not enough air between you and the light bulb to cause enough absorbtion to be seen.

QUESTION:
I was looking recently at old photos of the Space Shuttle in orbit. In one particular photo, an astronaut is outside the shuttle--untethered and over 300 feet from solid footing. He is, of course, equiped with his jet pack (an EMU or something like that), but my question is this: how, once the astronaut has exited the shuttle, does he remain at the same speed as the shuttle is going? Let me clarify.... The shuttle is going 17,000 mph or so in orbit, as anyone sitting inside is also...what makes a person who leaves the shuttle while it is in orbit stay in orbit along with the shuttle, despite having drifted 300 feet or so away from the departure point? The caption along with the picture described the astronaut as a "literal human satalite." Why doesn't the shuttle speed away from the man once he leaves?

ANSWER:
The only thing which determines the speed is the orbit in which the satellite moves. When the astronaut originally leaves the shuttle, he has the same orbit and moves with the same speed. But if he does something which moves him 300 feet away (for example, 300 feet farther away from the surface of the earth) he will now have a different orbit and a different speed. However, his percentage change in orbit radius is so incredibly small that the speed difference will be incredibly small also. In principle, if you wait a long time the two will get farther and farther apart.

QUESTION:
this is technically a "homework" question, but i disagree with the answer given in the textbook--hopefully you can tell me why their answer is valid. (or not) "an electron travelling at 0.25c and of rest mass 9.11*10^-31 kg collides head on with a positron with the same mass but travelling at 0.5c. when matter and antimatter meet in this way they anihilate eachother to produce energy, how much energy is released" the answers to the textbook just use E=mc², with the rest masses of the particles eg: E=2*9.11*10^-31*(3*10⁸)² E=1.64*10^-12 J However it seems illogical to me that the velocity of the particles (significant fractions of the speed of light) doesent influece the energy output. My initial reaction is that the relativistic mass (Mv) should be used instead.

ANSWER:
I would tend to agree with you that you should include the kinetic energy of the two particles in the total energy released. Thus, E=9.11x10^-31x[(1-.25²)^-1/2+(1-.5²)^-1/2]x(3x10⁸)²=1.79x10^-13 J. Then, for example, if the annihilation resulted in two photons (the most common), their energy would sum to 1.79x10^-13 J, not 1.64x10^-13 J as the book has it (there must be an error of a factor of 10 in your answer above).

QUESTION:
im a senior citizen who completed a short senior course on physics so maybe this is stupid.
l. is a photon also an electron?
2. does an electron ever break down into another particle and are all electrons charged?

ANSWER:
1. No. A photon is light, it has no mass and no electric charge; an electron has both.
2. No, an electron is a stable particle. It is possible to collide electrons with other particles and create new particles which do not include any electrons.

QUESTION:
Is it true (as people say) that if you are out-of-doors and trying to talk to a large group of people (e.g. a class of students) that you should stand upwind of your listeners so that the wind will carry the sound toward them rather than away? In other words, in a moderately windy environment, does the direction of the wind have an effect on how the sound travels through air?
1. I understand the Dopler effect, but that refers to a moving sound source. My question is a about a stationary source and receiver.
2. For the sake of this question, let's *not* factor in that the apparent sound of the wind changes when a person turns toward or away from the wind source. That may have more to do with the shape of the listeners ears. I am interested in the behavior of sound waves.

ANSWER:
The doppler effect refers to either a moving source or a moving observer (the fomulas are different, but the qualitative effects are the same). A wind is equivalent to a moving observer. If you stand upwind of the receiver, the sound will be doppler shifted to a lower frequency; downward to a higher frequency. But the intensity will be unchanged. If you think of your sound as being directed at a particular observer (like, for example a flashlight beam if it were light), then you could get in trouble if you had a crosswind which would result in the sound aimed at the observer missing him.

QUESTION:
Is is possible for something, a particle perhaps, to have mass but no volume? Matter is defined as anything that has mass and volume. But, is there anything that exists as a mass without volume? Much Mahalo for your help,

ANSWER:
Yes, such a thing is called a "point mass" or a "singularity". Black holes are thought to be singularities as are electrons.

QUESTION:
I may be wrong, but it seems to me that a freezer full of cold food is colder than the same freezer att he same temperature but filled with air. Is one actually a few degrees colder than the other?

ANSWER:
"Colder" and "at the same temperature" are contradictory. Colder means at a lower temperature.

QUESTION:
Would it be possible to engineer an antenna which could radiate extremely short pulses of only 1 period ? (e.g. for a 1GHz frequency, the pulse would last only 1 nanosecond ) Would it be possible to radiate a period and a half ? (e.g. for a 1 GHz frequency, the pulse would last 1.5 nanoseconds )

ANSWER:
It is possible but the engineering is not really the antenna but the electronics to generate the pulse. However, is you take exactly one period of 1 GHz sine wave, what you are left with is something which does not have a single well-defined frequency but is rather made up of all frequencies with 1 GHz being the maximum of the distribution. This is a classic example application of Fourier analysis of waves. This kind of "chopping" is routinely done with ultrashort laser pulses.

QUESTION:
Gravity and free fall. This is driving me crazy. Is the moon really in free-fall? How does this relate to the notion that the moon's "desire" to go straight is acted on by the earth's gravity and results in an ellipse? And astronauts – are they really in free fall, or just some metaphorical free-fall? Why don't the moon and astronauts just..you know..fall? I keep reading websites on this, but I am still confused.

ANSWER:
Is a stone which you throw horizonatlly in free fall (neglecting air friction)? It is because anything which is moving only under the influence of gravity is said to be in free fall. Imagine your throwing the stone faster and faster; it will go farther and farther until finally it goes all the way around the world and hits you in the back! This is a satellite. (This is not my idea, but rather was devised by Newton to understand the motion of satellites. Try it yourself at http://galileo.phys.virginia.edu/classes/109N/more_stuff/Applets/newt/newtmtn.html

QUESTION:
Imagine a man pushing a 10 kg cart horizontally across a frictionless plane, accelerating it from 0 m/s to 20 m/s in 10 s. What are the forces acting on the cart? I understand that there's F, the man's push, and W, the cart's weight. What should F be? Is it just simply: A) F = ma = (10 kg)(20 m/s - 0 m/s)/10 s = 20 N or B) F = ma + W = (10 kg)(20 m/s - 0 m/s)/10 s + (10 kg)(9.8 m/s/s)= 20 N + 98 N = 118 N? Shouldn't W be simply neglected because it is perpendicular to the direction of the object? Is the resistance the man feels when he pushes simply the inertial mass, or inertial mass plus weight? (I know you cannot add mass and force but well...) If W isn't neglected, shouldn't the object dig diagonally into the surface, by the usual addition of vectors?

ANSWER:
Your answer (A) is the right one. Your reasoning is correct that this force is not in the direction of the acceleration. What you have not noted is that the plane exerts an upward force on the cart which is (for this problem) equal to the weight so that the net force in the vertical direction is zero as it must be since there is no acceleration in the vertical direction. Weight is a force (which the earth exerts on a mass) and mass is mass, so it is the inertial mass which is the m in F=ma.

QUESTION:
I was just wondering why when you rub two items together (like your hand on carpet for example) heat is generated? Where does that energy come from?

ANSWER:
It comes from you. When you cause the two surfaces to move against each other you do work (a force acting over a distance) and work adds energy to a system, in this case heat energy.

QUESTION:
A recent experiment which involved converting energy into matter was accomplished at S.L.A.C. (short for Stanford Linear Accelerator Center). But while converting matter into energy is an easy feat, converting energy into matter is not so simple. Furthermore, whenever matter is being converted into energy, some of it is inevitably lost due to the second law of thermodynamics. However, you could compensate by disintegrating some rocks and adding in that energy too.

In Star Trek, the way the transporter works is by separating crew members at the atomic level and converting them into energy. Once they arrive at the appointed destination, the process is reverse. Granted, Star Trek is just a tv show, but let's say for the sake of argument that the transporter operates by converting people into energy and vice-versa.

1) In order to convert a person into energy, wouldn't that mean burning up that individual?

2) Would the person survive the procedure, or would the individual ceased to exist and be replaced with a replica, who was literally born into existence once the energy was reconverted back into matter with the information? (Note: I know this question sounds a bit philosophical but I'd be very interested in your opinion anyway.)

ANSWER:
Several comments on your question.

The second law does not allow energy conservation to be violated.

It is not really hard to convert energy into mass. If you take a CO₂ molecule and pull it apart (adding energy by doing work) it gets heavier; however, the amount of mass you make is too small to measure because chemistry is a crummy way to get or store energy. However, if you take the nucleus of an atom, say iron, and pull apart all the protons and neutrons in it, it will get measurably heavier.

What is tough is to convert energy purely into mass. An example of where this does happen is when a photon spontaneously creates an electron positron pair. This may be made to happen provided the photon has sufficient energy and it passes through a strong electric field (e.g. near some nucleus).

In your star trek question, "burning up" is not turning the person into pure energy, rather it is like the inverse of the CO₂ example above. Carbon in the person combines with oxygen in the air to make CO₂ thereby releasing some energy, but all the carbon and oxygen atoms are still there.

Your question #2 is too far out to be physics, particularly since there is no such thing as "beam me up Scotty".

QUESTION:
Hi. I've heard that particles (light, for instance) can be sped up to speeds much higher than the normally travel at. Could a similar process be used to accelerate the movement of radio waves?

ANSWER:
Particles may be accelerated to any velocity slower than the speed of light c (assuming that you have the energy to do it) but electromagnetic waves (including both light and radio waves) travel through empty space move with a speed of c, no faster, no slower.

QUESTION:
WHY COULDN'T INERTIA OR MOMENTUM BE CONSIDERED AS AN ETHER WAKE? IF AN OBJECT GAINS MASS AS IT ACCERATES WHAT IS THIS MASS, WHERE DOES IT COME FROM IF NOT SOME CONCEPT OF ETHER?

ANSWER:
I have no idea why you invoke the ether to explain mass increase, particularly since it is generally acknowledged that there is no such thing. Here is the orignin of "mass increase". If one defines linear momentum as (rest) mass time velocity like we do in classical physics, we find that the total linear momentum of an isolated system is not conserved. this is a very bad situation from the perspective of mechanics since the notion of a force is useless and the valuable ideas of energy have no validity. However, if we redifine the linear momentum as the quantity [1-(v²/c²)]^-1/2 times mass times velocity, both the linear momentum of an isolated system and its energy are conserved. So, you need not ever say that mass increases, it is just that momentum must be redefined to be useful. Many people choose to say that m is redefined and momentum isn't (still mass times velocity but a new kind of mass), but that is a point of view, not some kind of law.

QUESTION:
A recently published book on baseball pitching claims that an arm/hand assembly travelling at 31 mph will allow for a ball to be released at 95 mph. The author's contention is that, because of the law of conservation of momentum, the larger mass of the arm travelling at 31 mph will transfer momentum to the smaller mass of the ball, thus causing it to accelerate to 95 mph in order to satisfy that law. It is my contention that there can be no transfer of momentum unless there is a sudden decrease in velocity of the carrier due to an external force being applied, thus allowing the carrier to "give up" it's momentum to the unconstrained object (the ball). I proposed this question. What event has occurred from a point 1 millionth of a second prior to ball release and a second point 1 millionth of a second after release that causes momentum to be transferred? The masses of the arm and ball have not changed. Therefore, the only variable in the momentum equation to change is velocity. If the velocity is reduced by internal means, muscular relaxation, the momentum will be not be transferred to the ball but dissipated within the body. There is no external force, like a brick wall to stop the arm, therefore there can be no transfer of momentum to the ball. Am I correct here? Any help would be greatly appreciated.

ANSWER:
I feel quite certain that the speed of the part of the "arm/hand assembly" (as you call it) which is in contact with the ball is moving with the same speed as the ball when it is released. It is totally fallacious to talk about the speed of the "arm/hand assembly" because each part is moving with a different speed:

the shoulder has a small speed due to motion forward of the body

the elbow has a speed which is the vector sum of the velocity of the shoulder and the velocity of the elbow due to its rotation about the shoulder

the wrist has a speed which is the vector sum of the velocity of the elbow and the velocity of the wrist due to its rotation about the elbow

the hand (and ball) has a speed which is the vector sum of the velocity of the wrist and the velocity of the hand due to its rotation about the wrist

So, you see, it is not so simple.

QUESTION:
Studies over the years seem to indicate that lightspeed is slowing down. If so, is it because photon emmisions are somehow calibrated with the quanta about stable matter and is a result of those particles being in a state of deceleration?

ANSWER:
I think that this is quite speculative and not at all verified experimentally. Since the speed of light is what physicists call a "fundamental constant", the question is an important one in physics and philosophy since by definition, a constant cannot change. At this point, trying to understand why a constant of nature might change is perhaps premature.

QUESTION:
Why is the speed of light given by 1/sqrt(permittivity *permeabillity)? What is the great mistery behind such a simple relation? How these two parameters combine to give the speed of light? Why does the vacuum (nothing...) has physical properties such as permittivity and permeability?

ANSWER:
This is the great triumph of Maxwell's work in the 19^th century. There are laws of electromagnetism which can be summarized in four equations, now known collectively as Maxwell's equations. The quantity e₀ (permittivity of free space) is just a proportionality constant which tells you how strong the electric force is and, of course, it appears in the equations. Similarly, the quantity m₀ (permeability of free space) is just a proportionality constant which tells you how strong the magnetic force is and, of course, it appears in the equations. (In this context, there is nothing wrong with empty space having permittivity and permeability because one certainly does not need matter between charges or currents for them to exert forces on each other.) When Maxwell messed around with the equations he discovered that they could be rewritten as wave equations and that the speed of these waves had to be 1/[e₀m₀]^1/2. That this happened to be the speed of light was the point in the history of physics that we understood what was doing the waving in light waves--electric and magnetic fields.

QUESTION:
I've always understood comets or meteors crash into the ground at a very high speed. Is the meteor in the atmosphere for such a short amount of time, that it can't be slowed to terminal velocity

ANSWER:
I believe that would have to be the reason. Or else, it may be that the terminal velocity would not be particularly slow.

QUESTION:
If someone built a very tall vacuum chamber and dropped a bowling ball in it, assuming the ball is dropped a great distance from the ground, how fast could the ball fall? Would the Earth have a maximum pull on the ball? How long would it take to reach that speed?

ANSWER:
If the ball were a large distance from the earth (essentially infinite) the speed it would acquire when it hit the surface of the earth would be equal to the escape velocity, the speed a projectile shot straight up would have to have to totally escape earth's gravity. Of course, it would take infinite time to fall from infinitely far away, but if you were to drop it from some distance r away from the earth you could calculate the speed from energy conservation solving the following equation for the speed v:
v²/2-MG/R=-MG/r where R is the radius of the earth in m, M is the mass of the earth in kg, and G=6.67x10^-11(Newton's universal gravitational constant). Calculating the time would be possible but perhaps more involved than you want to get into!

QUESTION:
Is it possible for something to orbit a black hole?

ANSWER:
Certainly. In fact it is thought that there are binary star systems in which one star becomes a black hole and the other continues orbiting. Eventually, though, the orbiting partner will be sucked in.

QUESTION:
If uranium has a greater binding energy per nucleon than helium 4, then why is helium 4 much more stable?

ANSWER:
Because there are no decays which are energetically possible for helium 4. There is just "nowhere for it to go."

QUESTION:
If a mass of 10 kg compresses a spring 1m, then the spring constant k is 10/1 = 10N/m. And the elastic potential energy stored in the spring is therefore 0.5 x 10 x 1 = 5J (0.5kx2). However the gravitational potential energy lost by the mass is mgh = 10 x 10 x 1 = 100J. I thought these two amounts of energy should be the same. No other energy is added or removed. It is probably obvious but I'm stumped. What am I missing here?

ANSWER:
You have several things wrong. First, the weight of a 10 kg mass is 10x9.8=98 N, so that is the force which the spring exerts to keep the mass in equilibrium at a compression of 1 m. So, k=98 N/m. The energy of the compressed spring is now 49 J. Now, what is the gravitational potential energy? It is whatever you want! The gravitational potential energy is always arbitraty to within an arbitrary constant and so you may choose the level of zero gravitational potential energy to be anywhere you want:

If you choose y=0 where the mass is now, then the total energy of the system is 49 J+mgy=49 J.
If you choose y=0 where the mass was when the spring was not compressed, then the y=-1 m total energy of the system is 49 J+mgy=49 J+10x9.8x(-1)=-49 J.
If you choose y=0 to be halfway between, then y=-1/2 m total energy of the system is 49 J+mgy=49 J+10x9.8x(-0.5)=0 J.

My advice is not to memorize mgh but mgy which emphasizes that there is no magic place where h=0.

QUESTION:
When an alpha particle moves through an atom it will leave the atom undeflected if it is far enough away from the nucleus. What interactions are there with the electrons? Why do the electrons not attract and therefore deflect the positive alpha particle?

ANSWER:
Most certainly the alpha particle interacts with the electrons. But, the alpha particle has a mass about 8000 times bigger than the electron so it is like throwing bowling balls at bb's--the bowling ball is deflected only a miniscule amount. However, this is the mechanism by which alpha particles lose their energy going through matter; they have many collisions with electrons giving each electron a tiny amount of energy but eventually lose a large fraction (or all) of their energy. As you probably know, alpha particles don't go very far in matter--even a piece of paper can stop an alpha particle of a few thousand volts of energy.

QUESTION:
During a radioactive decay, when an electron is emited by the nucleus the overall charge on the nucleus must be positive, since there one more proton than before, why do equations not include the positive sign?

ANSWER:
I am not sure I know what you mean by the equations not including a positive sign. Here is what happens in negative beta decay: if the nucleus has too many neutrons and too few protons to be stable (somehow it knows!) and so one neutron spontaneously turns into an electron, a proton, and a neutrino. The electron and the neutrino are ejected and the proton stays behind in the nucleus. So electric charge is conserved, that is the remaining proton and ejected electron have zero net charge (the neutrino is uncharged) and the original neutron had zero charge. The atom left behind, however, has one too few electrons so it is a positive ion. There is also another kind of beta decay in which the nucleus has too many protons and too few neutrons to be stable; here one of the protons changes into a neutron, a positron (the antiparticle of the electron and with positive charge), and neutrion. Here the atom is left with one too many electrons, that is it is a negative ion.

QUESTION:
Imagine a lightsource (i.e Flashlight) located someplace incredibly far away from me, the space between the lightsource and myself is empty and there is nothing else in the universe. Once I turned the light on, would I eventually get to see the light no matter how small the source is, or would the light "wear out" at some point?

ANSWER:
It certainly never "wears out". But whether or not you can detect it depends on how intense it is, how far away it is, and the nature of the source. The simplest source to think about is a point source the intensity of which falls off like 1/r².Eventually, we will be far enough away that the intensity becomes so small that we must think of the light as photons instead of waves. The intensity will then be very few photons per second per square meter. In principle, though, as long as you made a very big detector capable of detecting a single photon and waited long enough, you would eventually see one. If you used a laser instead of a point source, the light would not fall off strongly with distance and, provided that your detector intercepted the beam, you would easily be able to detect it. However, no laser is really perfectly collimated and the comments for the point source would be applicable to some extent for large distances.

QUESTION:
Is there an upper limit as to how hot ordinary matter can get? Since temperature is really the average energy of the particles of matter, it would appear that eventually the average speed of the particles would approach the speed of light. Since nothing can go faster than light, what happens to super enegetic particles when more and more engery is applied to them? Do they get more massive? If so, at what temperature do these relavistic effects become significant?

ANSWER:
Although there is an upper limit to the speed a particle can have, there is no limit to how much kinetic energy it may have (because kinetic energy is not mv²/2 in relativity). For example, a particle with speed 0.9999 of the speed of light has ten times the kinetic energy as a particle with speed 0.999 the speed of light (only 0.1% slower).

QUESTION:
I recently read an essay written by Lee Smolin and he stated that protons and neutrons have the same mass, yet a neutron is heavier. Now it is my understanding that if any two things have the same mass then they have the same weight. So, is it possible that electromagnetism or weak force have an affect on gravity's pull on mass, thereby affecting the neutrons weight? If not, I am interested in your theory.

ANSWER:
I don't know the context of the statement, but unless you misunderstood his meaning, it is in the context of some theory of quantum gravity in which mass and weight have different meanings than in classical physics. You are right that we normally specify that W=mg and so all particles with the same m should have the same W.

QUESTION:
Why are electons considered negative? Is there anything that makes them specificly negative or is that just the charge that scientists assigned it?

ANSWER:
There is no good reason. All the mathematics of electricity and magnetism would be just the same if we called electrons positive. The important thing is that there are two kinds of electric charge (unlike gravitational mass for which there is apparently only one kind) and it is convenient to label one positive and one negative. The convenience is in the mathematics; e.g., if the force between two positive charges is repulsive, then so is the force between two negative charges because the force depends on the product of the charges. By the same token, the force between a positive and a negative charge will be attractive. Incidentally, it was Benjamin Franklin who originally labelled the the kind of charge which electrons happen to be as negative (electrons had not been observed individually in his day).

QUESTION:
I'm wondering how much slower light travels in non-vacuum environments, i.e. air, water, etc. Maybe you have a chart comparing the medium that the light is travelling in to speed in whatever unit, say % of c.

ANSWER:
There is a well known physical constant called index of refraction, n. It is defined as n=c/v where v is the speed in the medium. Some typical indices of refraction are air: 1.0003; water: 1.333; flint glass: 1.66; diamond: 2.42.

QUESTION:
Is electricity just magnetism at rest? Why do we treat electromagnetism as two separate vectors?

ANSWER:
You might say that magnetism is what happens when you put electricity in motion. You are right that we should not treat electricity and magnetism as two different things since they are really both parts of electromagnetism. We treat them separately for two reasons. First, this was the historical development and it has therefore become deeply embedded in the language of physics. Secondly, the associated phenomena are much easier to understand mathematically if we talk about these two vectors; the correct and rigorous way to discuss electromagnetism is to use what is called the electromagnetic field tensor, a single mathematical entity, but a tensor is a more difficult concept to grasp. It is the nature of electromagnetism that it cannot be fully described using a single vector field, but two vector fields can contain the information which a single tensor field does.

QUESTION:
If light exhibits Doppler phenomenon, an observer during a "blueshift" will measure photons of greater energy than are being emitted. How does this phenomenon account for energy conservation?

ANSWER:
Suppose that there is a stone at rest. It has zero kinetic energy. Now run by it with a speed of v; now it has a kinetic energy of mv²/2. No puzzle, right? The same is true of photons (except they cannot be at rest and their kinetic energy is their whole energy and not mv²/2). There is an important lesson here: the absolute amount of energy in a system is always arbitrary to within an additive constant, it has no real meaning. What matters is how energy changes (for example, if it doesn't change, energy is conserved.)

QUESTION:
How would you find the speed that the center of the earth is rotating when the outermost part of the crust is spining x amount of kmph?

ANSWER:
The very center of the earth has no speed (due to the earth's rotation) at all. If a point of the surface of the earth at the equator has a speed V and the earth has a radius R, then to find the speed v of a point a distance r from the earth's axis of rotation, you would use the equation v=Vr/R. It is important that it is the distance from the axis which determines the speed. Therefore someone at the equator has a speed V but someone not on the equator has a speed less than V and someone at the north or south poles has a speed of zero.

QUESTION:
What would the effect on the perceived gravitational pull of our planet if the rotation (or spin) of the planet was increased by a factor of 4? I would assume that the increased momentum at the outer edges would cause items on the surface to experience a lower gravitational pull. Unfortunately, I can not locate any equations to summarize this. Can you lend any assistance?

ANSWER:
The answer to your question depends on where you are. The effect would be zero at the poles and maximized at the equator. I will work it out for the equator. The first thing you need to do is calculate your acceleration. Since you are moving in a circle, your acceleration is v²/R=(2pR/T)²/R=4pR/T²=4x3.14x6.4x10⁶/(3600x24/4)=0.17 m/s²; here v is the speed of something on the equator, R is the radius of the earth, and T is the period ("length of day" which you stipulate to be 24/4=6 hours). This is the centripetal acceleration and the direction is toward the center of the earth. The sum of all forces on you must add up to your mass (m) times this acceleration. The forces on you are your own weight mg=9.8m (down) and the force that the ground exerts up on you, call it N. So we have N-9.8m=-0.17m, or N=9.63m. The force N is the force by which you perceive how heavy you feel, so you feel about 1.7% lighter than if the earth were not rotating; if you were standing on a scale, which measures the force you exert on it, not your weight, it would read 1.7% smaller than your actual weight mg.

QUESTION:
What are independent variable and dependent variable.

ANSWER:
An independent variable is one over which you have control in a particular experiment. A dependent variable is one which depends on other variables, one over which you do not have control. For example, suppose you want to know how the length (dependent variable) of a stick depends on its temperature (independent variable). Then you make measurements of the length of the stick at various temperatures and then analyze your data. The data analysis is often done by plotting the dependent variable as a function of the independent variable.

QUESTION:
c is a universal constant, why would this be? If light travels through different mediums the velocity is changed, correct? Like when light travels through a diamond, its speed is 88,000 mi/s. Is "c is a universal constant" stating that c can never be exceeded? Please explain, thanks!

ANSWER:
The universal constant is the speed of light in a vacuum, not the speed of light. What the usual relativity postulate states is that the speed of light in a vacuum is independent of the motion of the source or the observer.

QUESTION:
Is empty space granular? I'm asking because the more I read about the nature of "nothing" - the more it seems like "something."

ANSWER:
I don't think anybody really knows whether there is any limit as to how small a volume can be.

QUESTION:
It's generally accepted that all elements other than hydrogen were originally formed in the interior of stars. But couldn't those elements be created when hydrogen atoms collide outside a spinning black hole too?

ANSWER:
Anything which would give atoms sufficient energy to overcome the Coulomb repulsion of the nuclei could result in nucleosynthesis. However, anything other than inside a star will result in a negligible amount of such material.

QUESTION:
why does a drop of water burn the very hot oil ?

ANSWER:
It doesn't. What happens is that the oil boils the water which vaporizes.

QUESTION:
Is it possible to determine the spring constant of a bush (pine) ? (We need to estimate somebodies weight)

ANSWER:
A bush is a pretty poor approximation of an ideal spring, that is the amount by which a particular weight would compress it is probably not proportional to the weight (that is, a 200 lb person would probably not compress the bush twice as much as a 100 lb person). But, if it were a reasonable approximation of an ideal spring, you would merely have to calibrate it by measuring the amount of compression x caused by a known weight W. Then the spring constant would just be k=W/x.

QUESTION:
I am a high school physics teacher with a question concerning conductors. When a solid, conducting cylinder is charged, the static charge will reside on the surface only. When that same cylinder has moving charge (current), however, the current distributes itself throughout the cylinder. Why the difference?

ANSWER:
First, there are two kinds of electrons on a conductor: conduction electrons (typically on the order of one per atom) and the remaining electrons bound to the atoms. Then one can either add or subtract electrons to the material; this is the charge which, when equilibrium is reached, must reside on the surface. Similarly, if you put the conductor in an electric field, conduction electrons will move around but they will eventually come to rest with charge residing only on the surface. This is because if there is an electric field inside the conductor the conduction electrons will move, that is they will not remain at rest. Therefore, if you maintain an electric field inside the conductor, electrons will move in response to the force they feel and if you take them out on end and put them in at the same rate at the other end, a steady current will flow through the conductor. This is what a battery does: by maintaing a potential difference (voltage) across the conductor it therefore maintains an electric field inside the conductor which causes the charges to move. (It also acts like a "pump" removing electrons from one end of the cylinder and moving them to the other.)

So, in electrostatics the whole conductor is at the same potential, the electric field is only outside and perpendicular to the surface and all charge resides on the surface; for a steady current a potential difference is maintained which causes an electric field to exist inside the conductor which causes conduction electrons to move through the volume.

QUESTION:
I am not educated so please forgive me for the simplicity of the question. I realise that mathematically perfect shapes and flat surfaces cannot always exist in the natural world. If a perfect flawless sphere rests on a perfectly flat surface how much of this sphere is in contact with the surface? Does it matter how large the sphere is? I would also like to know how much weight would be concentrated at this almost negligible point of contact?

ANSWER:
A perfect sphere would be in contact with a perfect plane at only one point. It does not matter the size of the sphere. The sphere would push down on the plane with a force equal to its own weight (assuming the sphere and the plane are at rest), and all this force would be at the point of contact. The pressure on the plane, the force per unit area, would be infinite since the area of a point is zero.

QUESTION:
If I were able to place two photon detectors in space, one a mile above and one a mile below a hypothetical single atom that was just in the process of emitting a photon, would both detectors be able to detect said photon? In other words, is the direction an emitted photon travels in arbitrary or is it somehow predetermined, or is this a case of the famous wave/partical duality?

ANSWER:
Normally the emissions of photons is isotropic, that is a photon is likely to go off in any direction. But this is not because each atom is equally likely to emit in any direction, but rather because the whole collection of atoms whose radiation is being observed are randomly oriented. However, if the atoms happen to be aligned in some way for some reason, the radiation pattern will not be isotropic but will emit more intensely in some directions than in others. That is because each atom is, in essence, a little antenna and antennae have radiation patterns. Atoms usually have electric dipole radiation patterns.

QUESTION:
why don't a roof collapse from atmospheric pressure

ANSWER:
Because the pressure also pushes up from the underside.

QUESTION:
Can water be heated due to convection inside a satellite?

ANSWER:
The simplest kind of convection, free convection, depends on the buoyant force to move the fluid. Since the buoyant force is a gravitational effect, then in an environment like a satellite there would be no convection. However, convection has many other subtleties. You can get more information at http://scienceworld.wolfram.com/physics/Convection.html

QUESTION:
I was wondering, if you can (in theory) use antiprotons in a rocket, why can't you do it with say positrons, or antiquarks?

ANSWER:
You could, but, having smaller mass each positron annihilation would release far less energy. Antiquarks could not be used because we cannot isolate quarks.

QUESTION:
Why does the period of a pendulum increase as its lenght increases?

ANSWER:
Because when you solve Newton's second law you find a frequency which decreases with increasing length. The details may be seen at http://www.kettering.edu/~drussell/Demos/Pendulum/Pendula.html

QUESTION:
If you are in an air-filled spaceship and you open the door you are not sucked into space, the air inside rapidly expands out the opening and you are pushed out, not pulled. A vacuum is not like gravity, it does not pull or attract, something else has to push. Suction is actually some other force pushing matter towards the area of less density or pressure. For this reason, I say there is no force of suction, it's a misnomer. The absence of mass is not a force, it can't be. Decreasing mass or pressure doesn't create force, not for gravity or air pressure or anything. "Suction" is like "centrifugal force", a virtual force or an effect caused by other forces. Lift from an airfoil is from air pushing up from underneath, low pressure over the wing is not pulling it up. Which is not to say the leading and trailing edges and upper side curvature play no role, they do. The air effects above the wing work by increasing or enhancing the upward force on the bottom of the wing. It's easier to push something one direction if the force pushing back is less.

ANSWER:
Suction is a qualitative word, not scientific nomenclature. You are right that the net force pushes you out, a larger pressure on your back than on your front; similarly the airplane--a smaller force down on top than up on the bottom.

QUESTION:
This year I was taking both AP physics and anatomy and physiology together and found something which did not make sense. I asked both of my teachers and they are both right in their aspect. According to Bernoulli's equation, as a tube increases in diameter, the pressure increases in the tube compared to a smaller diameter. But in the circulatory system, when the diameter of the artery is decreased by the buildup of cholesterol on the walls, the pressure increases. Also, when I asked my mom, who is a doctor, she says to decrease the blood pressure of a patient they give medicine which dilates the arteries. This is the exact opposite of what they should be doing according to Bernoulli's principle.

ANSWER:
I think the problem here stems from the fact that blood is not an ideal fluid which is required for Bernoulli to be right, nor is the contact between the artery/vein walls frictionless. The more resistance there is to flow of the fluid, the harder you have to push it to move it along. Hence, an artery with deposits on it, while requiring the blood to move through with higher speed and therefore lowering pressure due to Bernouli effects will have a higher resistance to flow and require higher pressure to move it through. I recommend your reading the selection in Wikepedia about blood pressure.

QUESTION:
What determines the direction in which a photon will go when we consider that it is perpendicular to fluctuating electric and magnetic fields? What determines it will go forward or backward?

ANSWER:
At some instant and at some point in space, the electric and magnetic fields are perpendicular to each other. If you take the fingers of your right hand and curl them from the electric field to the magnetic field, then your thumb points in the direction of propogation. I could not find a picture specifically for this, but the picture to the right works if the green vector (labelled v) is the electric field, the blue vector (labelled B) is the magnetic field, and the red vector (labelled F) is the direction of travel of the wave. (Also, q=90^o.)

QUESTION:
Mike is going on a road trip. he's on the highway moving at a constant speed in his car. he notices that objects that he passes that are straight in front of him (the gravel on the road, the white dashed lines) move fast (as fast as the car), and as he begins to gaze sidewards, he notices that things don't move as fast as the things right in front of him (the road signs seem to be moving slower than the coke can right in front of him as he passes both). He notices that this trend continues right down to the mountains 30 miles to the side. they're are barely moving, if at all... Now you'll realize that none of the objects are actually moving; it's mike that's moving. everything is moving relative to him. is there any formula that can measure the "speed" of these objects where the relatives speeds of different objects, depending on their distance from mike?

ANSWER:
All objects at rest have the same velocity relative to Mike. But, the appearance is what counts to him. A distant mountain will appear to be the same size as a rock by the roadside. It takes the rock maybe 1/10 of a second to "move" its own size but the mountain may take 100 seconds to move its size. Hence, the mountain appears to be moving more slowly because the apparent sizes are the same.

QUESTION:
Would it be possible to get supplies to mars by creating a giant "pod gun" ? this "pod gun" would use a contained explosion of hydrogen (much like a real gun) to launch a "pod" of supplies into space.

ANSWER:
Any method which accelerates an object to a velocity greater than the escape velocity (the speed an object must have at the earth's surface to escape earth's gravity) would work. Questions of practicality and cost would be the determining factors.

QUESTION:
How do electrons leap from one side of an atom to another without traversing the space in between?

ANSWER:
What makes you think that they do? The proper way to think about an electron in an atom is to say that it is a probability distribution, that is it might be anywhere with a certain probablility being associated with each small volume in space. Hence you might make a measurement and find that the electron is on one side of the atom and later make a measurement and find it is on the other. This did not mean that it went discontinuously from one side to the other.

QUESTION:
I would like to know if a magnet's pole can be neutralized by insolationing or by anyother way .

ANSWER:
The only way to do that is to superimpose it on the opposite pole of another magnet. The important physical principle here is that the pole of a magnet can never exist alone, it is always accompanied by an opposite pole.

QUESTION:
It is given that there are two masses (bowling balls for instance) present in a vacuum. there are no outside forces acting upon them. no gravity, no air resistance, nothing. Both masses (the bowling balls) are the exact same shape and diameter. However, one has a mass of 10kg, while the other has a mass of 100kg. both objects are at rest relative to us as observers. If two equal forces where applied to both these objects at the same instant (say we put two identical rockets on these bowling balls) and fired them for exactly the same amount of time, would both objects go exaclty the same distance, or would one go farther then the other, and if so, which one? And regardless of the answer, why does this occur?

ANSWER:
You have hit on the central ideas of Newtonian physics. First, after getting either ball moving by your rocket, it will not stop after you turn the rocket off--it will keep going forever, so the question of which ball goes farther is moot. However, if you mean which ball goes farther during the time the rockets are on, it is the less massive one. This is because Newton's second law says that the acceleration of an object (the rate of change of its speed) is proportional to the force it experiences divided by the mass; hence, with equal forces the one with the smaller mass has the larger acceleration. Hence for equal times the less massive ball will acquire more velocity and hence go farther.

QUESTION:
Is it just arcing that causes a transformer to explode? Is there some flammable material (e.g. oil) inside it that causes the explosion? Seems like an arc would make the transformer melt, not explode.

ANSWER:
There is flammable material inside; if arcing occurs, there is likely a high current inside which provides the heating necessary to ignite the flammable material.

QUESTION:
Why do keepers of the famous clock Big Ben in London add or remove coins from the bottom of the pendulum to speed up or slow down the clock if the mass of pendulum has nothing to do with the pendulum's period?

ANSWER:
Because Big Ben's pendulum is not a simple pendulum, that is it is not a point mass attached to a massless string. It is what is often referred to as a "physical pendulum" and its period is determined by its moment of inertia and the moment of inertia depends on how much mass there is and where it is.

QUESTION:
I have a theory that the movement of a body in the universe is relative to other objects. Ergo, nothing can be absolutely still. Do you agree that everything in the universe is moving, and that no object is entirely at rest?

ANSWER:
If, as you suggest, everything is relative, then "at rest" is a matter of definition. That is, I can define myself, for example, to be at rest and then everything else in the universe moves unless it happens, as my computer is right now, to be at rest with respect to me. On a deeper level, nothing can be at rest because of the Heisenberg uncertainty principle because you cannot precisely know the velocity of something without being completely ignorant of where it is.

QUESTION:
When I get out of a car while wearing running shoes I get shocks from the metal door frame. However, when I exit the vehicle while wearing insulated boots I do not get shocks. My question is; All other conditions being the same, would I not still carry a static charge that would be discharged when I contact a proper ground? And why not?

ANSWER:
I am not sure what you mean by insulated boots, but what you want to do is have a good electrical contact between you and the ground when you get out. What is actually happening is that you have a static electrical charge on you when you get off the seat of the car. If you have shoes which have soles which connect you electrically to the ground, the charge leaks off. If the charge cannot leak off, it will seek a way to get off and will do so through the car (which, in spite of the tires being rubber and appearing to be not a good conductor, is actually a quite good path to ground). Before you touch the door, there is a large voltage (thousands of volts!) between you and the door because of your electric charge; this voltage causes a spark to jump which hurts. The best way to defeat this is to hold the door as you are getting out so the charge leaks off without there being a spark. So, my suspicion is that your running shoes have soles which insulate you from the ground but your boots do not. Incidentally, the problem is greatest when the humidity is low because a lot of water vapor in the air lets the charge leak off through the air.

QUESTION:
As a shotgun fires, the bb's make a pattern that gets wider and less dense with more distance. So how can light leave a small source and fill all the void in between for what seems could be an indefinate distance? i.e. the sun

ANSWER:
Because a shotgun is more like a flashlight than the sun. The light from a flashlight is pretty well collimated and spreads a little. The light from a source like the sun goes out in all directions. However, the intensity of the light from this kind of source gets smaller as you get farther away quite rapidly--if you go 10 times as far away, the intensity of the light gets 100 times smaller. That is why, of course, star appear much dimmer than the sun even though the sun is a pretty average star.

QUESTION:
if heat is the vibration of atoms why doesn;t it feel like vibrations but well heat?

ANSWER:
The vibrational frequency of a typical atom in a room temperature solid is on the order of 10 THz, that is about 10 million million vibrations per second. To put this frequency into perspective, you cannot hear more than about 20,000 vibrations per second. Your body has no mechanism by which it can respond to such a rapidly changing stimulus. Furthermore, the vibration of a single atom against your skin would be imperceptible and the atoms are all vibrating with random phases.

QUESTION:
if gravity is approximated by a constant and if the frictional force is proportional to the velocity, show that a free-falling body (i.e. no restoring force) approaches a terminal velocity

ANSWER:
Since the downward force is mg (constant) and the upward force is bv (b is constant, v is speed), the net force will be mg-bv down. The frictional force starts at zero but as v increases the net force gets smaller. Eventually the speed will be big enough that the net force will be zero, so the speed will remain constant. The terminal velocity will be mg/b.

QUESTION:
If you wanted to use your laser beam to hit a space station that was traveling above the atmosphere and just above the horizon, would you aim the laser above, below, or directly at the station YOU SEE FROM EARTH? (the index of refraction of space is exactly 1.0, while the index of refraction of air is about 1.001)

ANSWER:
Since light is reversible, that is light traveling from you to the space station will follow the same path as light traveling from the space station to you, you should visually aim at it.

QUESTION:
Hi, quick question, a few friends and I had a little debate the other day. Basically the premise of the debate was that if humans somehow started to dump all our garbage into space the mass of the earth would be affected enough to somehow affect earth's orbit. Their contention was that everything is produced by the earth as in what humans make from it therefore if we started jettisoning it into space it would affect earth's mass to alter its orbit however miniscule. I saw something really wrong with this, in my view there are many variables not being taken into account here that affect earth's mass and its relation to the sun and its orbit and that garbage is too small a variable or another counteracting variable would negate any effect it could have if it was sent into space. Yes a little bit of a weird topic lol, but any insight would be appreciated.

ANSWER:
If the earth's mass suddenly decreased by half, the period of the orbit (one year) would be totally unaffected. The period of the orbit of a satellite is independent of its mass if the sun's mass is very large compared to the earth's mass (2x10³⁰ kg vs. 6x10²⁴ kg, a ratio of about 3/1,000,000). To be exact, it is the reduced mass of the system which matters; that would be m_sunm_earth/(m_sun+m_earth), but, since m_sun>>m_earth, the reduced mass is incredibly close to m_earth, and the dependence of the orbit on the mass is completely negligible. Technically, however, your friends are right that a change of mass will affect the orbit; it is just that for even a huge change in mass (a large fraction of the earth's total mass) the effect would be so small as to be unmeasurable.

Another problem to consider is the possible disruption of the earth's orbit because of how the mass was ejected. For example, in the extreme case where you jettison half the earth's mass into space with some velocity the remaining half would recoil with the same velocity which would certainly seriously alter the orbit. But if you jettisoned a million tons, the earth's recoil would be negligible.

QUESTION: ;
can you please explain nutrinos in basic terms?

ANSWER:
Many radioactive nuclei undergo a decay called beta decay. One kind of beta decay happens if a nucleus has too many neutrons (which have no electric charge). Somehow nature knows this and takes one neutron in the nucleus and turns it into a proton; but electric charge must be conserved, so the appearance of a positively charged proton necessitates the creation of a negatively charged particle, so an electron is ejected from the nucleus. It is this electron which is the "radioactivity". Back in the 1930s when beta decay was first discovered a most disturbing thing was observed: the electrons which were ejected came out with a broad range of energies. This was disturbing because each electron left behind the same thing (that is a nucleus with a particular amount of energy), so the range of electron energies implied that the energy was not conserved by beta decay. This principle, energy conservation, is so dearly held by us physicists that we invented a third particle, the neutrino, which had no mass and no electric charge and carried off the right amount of energy to insure that energy was conserved. A remarkable fact is that, because it interacts so incredibly weakly with matter, the neutrino was not experimentally observed until the late 1950s. So nearly 30 years elapsed before this hypothesized particle was observed, yet no self-respecting physicist doubted its existence!

Neutrinos have been in the news lately because of the so-called "solar neutrino problem". We believe that we understand very well what goes on inside the sun and yet the number of neutrinos which we observe on earth is considerably fewer than the number predicted by our models of stars. This problem has recently been solved by measurements which find that the neutrino is not really massless but has an extremely small mass (much smaller than the electron, the lightest of "everyday" particles). I will not attempt to explain how this solves the puzzle, but it does!

QUESTION:
Does gravity have a speed at which it travels? To clarify, if you teleported two objects to some incredibly far away & empty region of space, so the only noticeable force of gravity would be the two objects pulling each other together, upon arrival by teleportation like "popping in to existence" would there be a delay before they begin pulling each other?

ANSWER:
I do not believe that the speed at which a gravitational field propogates has ever been measured. It is generally believed to propogate with the speed of light. But whatever its speed actually is, nobody would believe that it is instantaneous.

QUESTION:
I have some demonstration capacitors that are rated 1F at 5V. Is this correct then that it can hold a static charge of 5C? I've always thought that 1C of static charge was enormous. Am I missing something? Is there a dielectric out there that allows this?

ANSWER:
Those capacitors could not possibly be 1 F. They are probably 1 mF.

QUESTION:
Is a satellite that is orbiting earth (and not decaying in its orbit) in equilibrium? I say no, because only 1 force (gravity) is acting on the satellite--otherwise it would move in a straight line. My coworker says that inertia or momentum is balancing the gravity and that therefore the satellite is in equilbrium. What is the real answer?

ANSWER:
You are right. It is clearly accelerating (velocity always changing direction) and so cannot be in equilibrium.

QUESTION:
Is there a way to change/slow down the rate of radioactive decay...for example, Tc99m half life is 6.01 hours. Is there a way to change that time, or slow it down?

ANSWER:
Not unless you slow down time itself, for example if the radioactive nuclei had a very high speed in the laboratory, they would live much longer because of time dilation.

QUESTION:
in my gcse physics lesson the teacher explained that an electron is given out by a nucleus when it changes during beta decay and a nuetron changes into a proton. Why is the electron made when the neutron changes? also is there such a thing as anti elements for example the exact opposite of hydrogen?

ANSWER:
There is also a third, chargeless particle, the neutrino, which is a product of neutron decay. It is not simple to answer a question like why the electron is ejected; that requires understanding the theory of beta decay (that is what this is called). One easy way to believe that an electron might come off is that the total electric charge of the universe must remain constant, that is you cannot create or destroy electric charge. If a proton appears, so does 1.6x10^-19 Coulombs of charge; to keep the total charge equal to zero, -1.6x10^-19 Coulombs of charge must appear which just happens to be the charge of an electron. And yes, antihydrogen (consisting of an antiproton and a positron) has been observed. Check out this story from CERN.

QUESTION:
Quantum mechanics views force interactions between particles as an exchange of other particles, such as the photon. General relativity views the gravitational 'force' as an artifact of space-time distortion. How does general relativity handle the other 'forces' - electromagnetic, weak and strong? Does general relativity also view these forces as manifestations of space-time distortion? Or, does it view gravity as a special case distinct from these forces?

ANSWER:
Some work has been done in extracting electromagnetism from the equations of general relativity with mixed results. It is pretty fair to say, however, that gravitation and all other forces of nature are not reconciled. A theory of "quantum gravity" is one of the "holy grails" of theoretical physics.

QUESTION:
I have seen many warnings about the possibility of a hydrogen explosion when charging batteries. I know hydrogen is produced, but the volume in the battery seems small, many have a method of venting and the ignition source is outside the battery. Are there any scientific studies that confirm the culprit is hydrogen? I have been looking on the internet but have had no luck finding an authoritative source.

ANSWER:
Hydrogen is very dangerous, even in small amounts if confined. Venting makes the danger less acute but not nonexistant. Explosion is a relatively rare event with batteries, but not to be taken lightly.

QUESTION:
Is it possible to heat water vapor to a plasma state? Can it be done on earth?

ANSWER:
Any gas may be converted into a plasma (which is just a mixture of unbound electrons and positive ions). My guess is that water would probably dissociate into H and O either before or simultaneously with ionization. It doesn't take all that much energy and could easily be done on earth.

QUESTION:
If I tear a piece of paper, what is happening at the subatomic level at the torn edges? Are the electrons/subatomic particles getting ripped out of their positions? And then do they fly off into the air or remain glued to their original position?

ANSWER:
Solids hold together by adjacent atoms bonding to each other. Ripping a piece of paper simply breaks these bonds. This will be a pretty violent process on the microscopic level and some atoms and clusters of atoms are sure to end up leaving the paper altogether.

QUESTION:
My 7 year old daughter has a "simple" physics question, but I want to give her a precise answer in terms she can understand. I am hoping you can help. Here it is: At sea level, would a soccer ball which is completely deflated (and collapsed) have a greater or lesser weight (as measured on a standard scale) than one filled with helium? My supposition is that the scale weight goes down when filled with helium, even though the overall mass is increased by the helium itself. Is this correct? That's a concept she can't understand and I want to explain it if possible.

ANSWER:
Your question has an ambiguity in it: you ask about the weight "as measured on a standard scale". However, a standard scale does not necessarily measure the weight of an object sitting on it, it measures the force you push down on it with. So, a 10 pound weight on the scale and on which you are pulling up with a force of 4 pounds will only "weigh" 6 pounds according to the scale. So, let me address the question in two parts.

Which has more weight, the empty ball or the full ball? Obviously, the full ball since it has the weight of the ball plus the weight of whatever it is filled with.
Which will have the greater apparent weight as measured by the scale? Here a new force, the buoyant force, comes into play. When you put an object into a fluid (air is a fluid) there is an upward force on it which is equal to the weight of the displaced fluid. Since you are dealing with a 7 year old, just give her a simple example of a buoyant force: e.g. a soccer ball filled with air on the bottom of a swimming pool pops to the top because of the buoyant force; the buoyant force on the soccer ball in air is just less than in water because water is more dense than air. So, assuming that the helium is at a pressure (close to atmospheric) not too high, there will be an upward buoyant force (equal in magnitude to the weight of an equal volume of air) greater than the weight of the added helium, and so the apparent weight will be less than the empty ball.

QUESTION:
I am having trouble reconciling these two principles: (1) the velocity of light is independent of the velocity of the source, and (2) in a uniformly moving system you can't tell how fast you are going. Suppose you are in a uniformly moving system and you set up a light source that sends out two beams simultanously--one in the direction of the motion of that system and one in the opposite direction. You have two detectors located at equal distances from the source (thus detectors and source are in a straight line). Wouldn't the detector located "behind" detect the light before the detector located "ahead"?

ANSWER:
To understand relativity, you have to "believe" the postulates. Essentially what you must accept, as nonintuitive as it may seem to you, is that the speed of light is the same as seen by any observer. The result of this assumption totally upsets our ideas about what space and time are. The experiment you describe is one of the classic examples illustrating how the notion of time is different. The concept is that of simultaneity: classically, if I determine two events to happen simultaneously, I expect anybody else in the universe to agree with me. (Note that "determine" is different from "see": if I see one event and then one year later see a second event, but the second event happens somewhere a light year from the first, then I determine them to be simultaneous.) The experiment you describe will have an observer on the moving system see the events happen simultaneously but an observer at rest will see the two events to be not simultaneous in the way you describe. It is an inescapable consequence of the fact that the speed of light is the same as seen by any observer.

QUESTION:
We all know carbon dioxide sublimes as "dry ice". Is the same true for carbon monoxide? Both have a triple point. I've read conflicting things and was hoping you could provide a definitive answer. And if not pressurized liquid gas released and evaporating into a solid, how then is frozen or solid carbon monoxide possible?

ANSWER: (provided by S. P. Lewis)
Whether or not a solid in equilibrium sublimes to the gas phase as temperature or raised, instead of melting to the liquid phase, depends on the (presumably fixed) pressure at which the experiment is done, relative to the triple point of the substance. If the experiment is done at a pressure below the triple point, then a constant-pressure line in a P-T phase diagram crosses the solid-gas coexistence curve. This means that raising the temperature of the solid eventually leads to sublimation. Conversely, if the operating pressure is above the triple point, then a constant-pressure line crosses a solid-liquid coexistence curve and a liquid-gas coexistence curve. This means that raising the temperature of the solid eventually leads to melting, and further heating eventually leads to boiling. For carbon dioxide, the triple point is at pressure 5.2 atm and temperature -57 C. If we assume the experiment is done at ambient pressure (i.e., 1 atm), then we would expect solid CO2 to sublime to gaseous CO2, which it does -- hence 'Dry Ice'. The triple point of carbon monoxide, however, is at pressure 0.15 atm and temperature -205 C. Ambient pressure is well above the triple-point pressure, and therefore, under these conditions, solid CO would not sublime on being heated. Rather, it would melt and then eventually boil.

QUESTION:
Would the shape of a balloon (i.e., regular 9" round; oblong 9") with the same amount of helium affect the rate of ascent? I would greatly appreciate your answer/input and any specific guidance that you can offer us. We have read your groundrules and are not using "The Physicist" to do our homework. In order to answer this question, my son and I have been researching topics such as hot air balloons and gravitational force by visiting our local library. However, our library is very limited and provides few good science books. Therefore, we have been performing various topic searches through Google during the past several weeks in order to answer this question ourselves.

ANSWER:
There are several things to consider. I would like to just answer your question without the complications of what happens at distances high above the ground where temperature is much colder and pressure (of the atmosphere) much lower. In first approximation, the only things which will determine the motion of the balloon are the mass and volume of the baloon+helium,; let's call those m and V respectively. The weight of this balloon is therefore W=mg where g is the accelleration due to gravity; this is a downward force. Now, Archimedes' principle tells us that there will be upward force (buoyant force) equal to the weight of the displaced air, B=rVg where r is the density of air. The total force on the balloon is therefore B-W=rVg-mg upward. Because of Newton's second law, the balloon will therefore have an upward acceleration of a=(rV/m-1)g which is independent of its shape. However, in the real world there is another force which cannot be neglected and that is the air friction the balloon experiences when it starts moving. This depends in very complicated ways on the geometry of the balloon and is best studied experimentally, I think.

QUESTION:
The triple point of Hydrogen is about 13.8 K and the temperature of Universe is about 2.73 K. This means that all the Hydrogen atoms in the universe must be in solid state. Why don't these tiny particles coalesce and form a hyge ball of solid Hydrogen, weighing about 10 to the power of 49 or 50 tons, which would then implode under its own mass and lead to another Big Bang? Would this scenario ever take place?

ANSWER:
No, it does not mean that the universe is solid because the pressure of the intergalctic medium is incredibly small. Hence the intergalactic medium is essentially gaseous hydrogen.

QUESTION:
I am a senior high school student, and I have a question pertaining to thermodynamics (actually originating in my chemistry class). My teacher asked us the following question "Which has more heat: 1000g of water (heat capacity of 4.18J/°Cg) at 60°C or 1000g of steam (heat capacity of 2.01J/°Cg) at 105°C?" First of all, I was under the impression that heat is defined as the transfer of energy during a reaction, and that objects don't have a property called "heat". Presumably, he was looking for the substance which had the greater internal energy. In this case, I would answer that the steam had the greater internal energy, since it had (presumably) been heated as a liquid, then boiled and then heated some more to its final temperature. Thus, it would have greater average kinetic energy, and greater intermolecular potential energy than the water. I realize that some complexity arises from the state change and pressures/volumes etc. in gases, but I'm not sure exactly how. If you could shed some light on this, it would be greatly appreciated.

ANSWER:
Your semantics are sound, i.e. you should be thinking about internal energy. Your reasoning seems sound also since you need to add energy to heat the water, add energy to vaporize it, add energy to heat the steam.

QUESTION:
We are taught that E fields, M fields and EM fields are real entities and that they contain an energy density; and that (changes in) their influence propagate at lightspeed. There is an equivalence of mass and energy, and energy must be conserved. If these statement are all true, why is the mass of charged matter (e.g., an electron) constant? Does there not exist a continuous flow of energy radially outward from a static charge, for example, as the influence of its electric field propagates to ever larger volumes of space?

ANSWER:
Because a field has an energy density does not imply that energy flows. In fact, if you compute the rate at which energy leaves a volume surrounding a static charge, the answer is zero. Charges radiate energy only when they accelerate and the energy loss is taken from the kinetic energy of the accelerating particle, not its rest mass energy.

QUESTION:
I read that electrons at SLAC are accelerated to speeds of 0.999 999 999 948c. What are the specific products when electrons moving at this speed collide with other particles? Could you list some of the reactions produced at this speed? I would also like to know the applied EMF in volts needed for achieving the above speed, so that I can determine the energy of the accelerated electrons.

ANSWER:
The huge number of possible reactions depending on the target make it impossible to answer your first question. However, you second question can be answered pretty easily. However, you want to calculate the total energy E from the speed from which you can infer the voltage which must have been applied. The total energy is E=mc²/[1-v²/c²]^1/2. The arithmetic is a little tricky for v so close to c, but I find that E=4.9 GeV. This is the total energy, so to get the kinetic energy you must subtract the rest mass energy; but the rest mass of an electron is about 0.511 MeV=0.000511 GeV, so it is negligible. Hence, the EMF you seek is about 4.9 x 10⁹ volts.

QUESTION:
when you see a rainbow, you always see part of a circle. How high must you rise to see the full circle? Please include some references in your reply so that I can learn more about this fascinating topic.

ANSWER:
There is a pretty clear answer to your question at http://www.wonderquest.com/rainbow-circle.htm.

QUESTION:
my question to you is: "Where do the bubbles in softdrinks like coka cola go in zero gravity?" Will they rise to the surface, or will they stay in the same place? If so, will the bubbles keep growing? I can imagine that mass matters, that the bubbles in a mass of soda the size of a planet, 'would' rise to the surface, but how about smaller masses.

ANSWER:
Bubbles rise because of the buoyant force. But, in a no-gravity situation, there is no buoyant force. Therefore the bubbles should not move at all. I guess the whole ball of softdrink would become a froth of bubbles eventually but the evolution would probably be complicated to describe.

QUESTION:
OK. I have been thinking about this for a very long time, however since i do not possess the intimate knowledge that a well-versed person in the ream of physics might have. My question is this: From my understanding, there are four main forces which keep the universe together. One of them is gravity. Gravity affects the heavens and all that it encompasses even light. Light is bended by the gravity exerted from a massive object. From what ive learned, this is one way black holes are observed. As is commonly known, nothing can escape the gravitational pull of a black hole, not even light. So what we have are two extremes: in one extreme, a beam of light would travel (theoreticlly) in a straight line if no force of gravity was imposed on it and in the other extreme, light is bended so far that it is incapapble of escaping when it enters a supermassive graviational field. The question i have is is there a medium between the extremes? Would it be possible for a beam of light to orbit an object of a specific mass, trapping it in orbit?

ANSWER: (answer provided by L. A. Magnani)
Yes, light can orbit around a black hole of any given mass. The key question is, how far from the singularity can the light maintain a circular orbit? It turns out that, according to General Relativity, light can maintain a circular orbit at 1.5 times the Schwarzschild radius from the singularity (the Schwarzschild radius is 2GM/c² where M is the mass of the black hole, G is the gravitational constant and c is the speed of light. This region is sometimes called the photon sphere. Inside 1.5 times the Schwarzschild radius, no circular orbits exist; all orbits are unstable and all objects moving inside of this distance fall into the black hole.

QUESTION:
Two identical balls are attached together with a 3-foot length of string. Hold one ball and allow the other ball to stretch out the string. If the "system" is dropped from a height of about 5 stories, why do the balls come together before they hit the ground?

ANSWER:
The only explanation has to be air friction. The leading ball behaves like a freely falling ball which accelerates until it reaches its "terminal velocity"; it does not continue accelerating because there is an upward force due to air friction on it and this force gets bigger as the velocity gets bigger. The upper ball, however, is in the wake of the lower and therefore has a smaller air friction force on it.

QUESTION:
Ok, I have a friend of mine that thinks if (in a vacuum with no gravitational interference) you were in a spaceship and turned the rockets on you would begin accelerating and continue to accelerate even after the rockets were turned off. I thought that according to F=ma or a=F/m you would stop accelerating and only maintain the velocity you had attained at the moment you turned the rockets off. Is my thinking flawed or did I read Newtons laws correctly?

ANSWER:
Your friend is dead wrong.

QUESTION:
I am trying to vibrate a tissue with a sound source that is directed at the tissue, but not in direct contact with the tissue. I have been told that using acoustic waves will provide this type of push/pull motion. That is, they will push the tissue and actually pull it back to equilibrium, as opposed to just allowing the tissue to come back to it's equilibrium position on it's own before the next wave hits. I have also heard that ultrasound waves do not have this property. That is, they result in static displacement and will not allow the tissue to return to equilibrium unless the source is off (as is the case in pulsing ultrasound). A co-worker told me this was not true about acoustic waves. Example the front of a speaker only vibrates in and out because the membrane comes to rest on it's own before the next vibration. Can you tell me the properties of these waves in this kind of situation and maybe a source of information?

ANSWER:
There is no simple answer to your question. Essentially your question has to do with driven oscillations. If we model the tissue paper as a simple harmonic oscillator (which you seem to be implying), then it has a characteristic natural frequency. If you drive it with a frequency equal to that frequency, it will have a large amplitude of oscillation with a frequency close to its natural frequency (this is called resonance). But, if you drive it with a different frequency, the paper, after some initial transient behavior, will oscillate with the driving frequency, not its natural frequency. The farther you are from the natural frequency, the smaller the amplitude of the response will be.

QUESTION:
I have to do a physics project. Its called an egg drop. We can only use a brown lunch bag, 3 straws, the card board of a toilet paper roll and tape to create a device that will deliver our egg safely to the ground from 4 diffrent hights. Do you have any design tips or suggestions?

ANSWER:
I will not try to design something, but I will tell you what you need to do. To break an egg you must deliver a force to it. Force, according to Newton's second law is mass times acceleration. So, since you have no control over the mass of the egg, you must minimize the acceleration which it experiences to minimize the chance of its getting broken. To do this you maximize the time it takes for the egg to come to rest. Another issue (besides the magnitude of the force on the egg) is how that force is distributed: an egg dropped on a nail is much more likely to break than if you could take the force exerted by the nail point and redistrubuted it over a bigger area of the egg's surface.

QUESTION:
Lets say as an example that the muzzle velocity of a particular rifle is 700 miles per hour. If you fired the gun on an aircraft that had a constant velocity of 700 miles per hour, would the velocity of the bullet relative to nature be 1400? My next question is if you fired the bullet backwards, would the bullet's velocity be Zero (relative to nature, not the aircraft)?

ANSWER:
Yes and yes, assuming that we neglect air resistance.

QUESTION:
I understand the "electron gas" model of metal, but one thing I've never heard addressed is what happens at the surface of the metal. In a simplistic model, we say: An electron travels some distance until it collides with something. After the collision, it starts a new path in a random direction. If an electron starts near the surface of a piece of metal, and travels towards the surface such that its trajectory would take it outside the metal before it collided with something, what happens? Does the electron temporarily leave the metal before being pulled back by electric forces? Can a collision with the surface be treated as one of the other collisions where the electron starts a new path in a random direction? Or should this be treated as an elastic collision, as if the electron were a ping-pong ball bouncing off a wall (angle of reflection = angle of incidence, etc.) ?

ANSWER:
Perhaps it is best to just examine the problem more classically. If an electron comes shooting out of the surface (which it might), it will have a positive image charge inside the metal which will attract it back. On a more microscopic level, if an electron is removed, an equal amount of positive charge is left behind which will attract it back. If, however, the metal is very hot so that there are electrons of sufficient kinetic energy to escape, then electrons will flow out the surface; this is called thermionic emission. I think you should not think of a "collision with the surface"; the electron either collides with something close to the surface (which is, at a microscopic level, not well defined) or it doesn't.

QUESTION:
I read somewhere that tachyons can go faster than light. How?

ANSWER:
Tachyons are hypothetical particles. A tachyon has never been observed. The theory of relativity does not forbid particles to have a speed greater than the speed of light, but you "cannot get there from here", that is you cannot take a particle with speed less than the speed of light and accelerate it to a speed greater than the speed of light.

QUESTION:
Is it possible that the gravitational constant varies with the composition of the mass? For instance, could a kg of ice have a slightly different gravitational constant than, say, a kg of iron?

ANSWER:
Of course no scientist likes to say "impossible", but in some sense the very name "gravitational constant" automatically insures that what you ask is impossible by definition. Then, since the only other things that gravitational force depends on are mass or distance between attracting objects, if you get a force different than what you expected, then you probably made an error in measurement of mass or distance; the gravitational constant is simply the proportionality constant in Newton's universal law of gravitation.

QUESTION:
Hello, I have been trying to find out how to calculate the force on an object when this object is rotating around a point. I know that this is called the centrifugal force and that it is calculated by [F = r * m * v²]. However, every place I look will not give me units of measurement. Is the Force(F) in Newtons? is the radius(r) in Meters? is the mass(m) in Kilograms? Is the angular velocity(v) in revolutions per minute? Thanks a bunch

ANSWER:
First of all, it is not called centrifugal force, it is centripetal force, a force pointing toward the center of the circle (from the Latin centrum=center + petere=to seek). A centrifugal force (from the Latin centrum=center + fugere=to flee) points away from the center and is what phyicists call a fictitious force, i.e. it does not exist. Secondly, the force is not what you have it but rather F=mv²/r. Now the units are correct, (kg m²/s²)/m=kg m/s²=N.

QUESTION:
How can an particle, in real life have a net mechanical energy of less than zero? Energy can be taken away from a system resulting in a negative change in energy, but how can its total mechanical energy be less than zero. I tried to justify this question with the fact that potential energy is often relative, such as in the case of gravitational potential energy, so all of the movement of a particle happens "below" this zero reference point. But I am still feeling unsettled about this. Is there a better answer?

ANSWER:
Only kinetic energy is definitively positive. Potential energy is always arbitrary within an additive constant. What really matters is how energy changes, not what energy is.

QUESTION:
A photon travelling from a distant part of the universe is red-shifted by the time it reaches earth. The photon has less energy when it arrives. Where has the missing energy gone?

ANSWER:
For starters, you should not talk about photons and gravity simultaneously since quantum mechanics and general relativity are not compatible with each other. But the fact remains that a photon leaving some very large mass will be red shifted so energy has been lost. The source of the gravitational field will gain that energy.

QUESTION:
Has the idea that the speed of light is actually slowing down been debunked? Do both gamma rays and radio waves move at 183,000 mps? If I turn on a light bulb in outer space will the EM radiation from that bulb ever stretch out to the point of being below the visible spectrum? Will it become infrared then microwave then radio wave?

ANSWER:
The question of whether nature's constants are in fact constant over very long times is a question of interest to physicists. There is no evidence that the speed of light is not the same as it has always been. Electromagnetic radiation of a particular wavelength moving through empty space will maintain exactly the same wavelength regardless of the distance from the source.

QUESTION:
If you have a ballon filled with helium and you let it go it will rise. As altitude increases, air pressure decreases and the ballon expands. But as altitude increases, temperature decreases and causing the ballon to contract. Will it pop?

ANSWER:
The drop in pressure plays a more important role than the decrease of temperature, so it will want to continue to want to expand going to higher altitudes. However, whether it pops and when are determined by things like what the balloon is made of, how much helium was initially in it, etc.

QUESTION:
I was just wondering, positrons and anti-protons have the opposite charges of electrons and protons and anti-neutrons have the opposite charge of neutrons. But I was under the impression that neutrons have zero charge...so a negative neutron would be the same as a normal neutron.. What's the difference!?

ANSWER:
The antiparticle of a neutral particle is also neutral. But they are not the same particle since there are other quantities besides electrical charge which determine the properties of an elementary particle.

QUESTION:
Last summer I was paddling my canoe on an Ontario lake at late evening. The air and water were almost perfectly still. I was smoking a pipe, and as I paddled I obviously exhaled regular puffs of smoke. But when I looked beside me, I noticed that the more or less coherent clouds of smoke were travelling along with me at almost the same speed as the canoe! In fact, they formed a very shallow arc sweeping away beside me and downwind from the very slight breeze. But how is this possible? Why wouldn't each cloud smack into the still air and be stopped immediately? In an aerial view, the smoke should have looked like a trail of breadcrumbs, but it looked more like a flight of geese. I've repeated the experiment many times, always with the same result.

ANSWER:
If you drop a bomb from an airplane, does it stop immediately (its forward motion) when it hits the still air? No, in fact it will approximately continue on with approximately the same forward speed it had when you dropped it and eventually hit the ground directly under you. In the real world, there is some air resistance and so the bomb will slow slightly and eventually hit the ground somewhere behind your position. This is evidently what is happening with your smoke. Suppose that you blow a smokering forward in a room with still air. It moves forward with a pretty constant speed and eventually slows down.

QUESTION:
I was in Physics class and we were discussing half-life. My teacher said that if I keep taking half of something away, the original piece will never be zero, or will never disappear. I remembered a problem I heard. If a man shoots an arrow at a wall, will it ever reach the wall? Because first it has to reach the half-way mark, then half of the rest of the way, then half of that, and so on. So theoretically, the arrow won't reach the wall. I know in reality it will, but how else would you explain this question?

ANSWER:
The notion of half life is a statistical one. That is, the rate of change of the decaying particles is proportional to the number of particles; so if you find that a sample of 1,000,000 particles decay at the rate of 1000 per hour, then 2,000,000 particles will decay at the rate of 2000 per hour. Then half life is a useful concept. But when the number of particles gets small, this proportionality is no longer true, so half life is no longer a useful concept.

QUESTION:
what would be when an object is obliged to do a work that is greater than its energy? for example assuming that there is an object at the top of an inclined plane an it has only a potential energy of mgh. And it is released to go to the base of the plane but the work must done by the friction is greater then mgh for instant 2mgh. Also the friction force is smaller than the component of weight, mgsin&. It must go to bottom because of gravity but it has not enough energy to go.What would be???

ANSWER:
You are apparently assuming it starts at rest. Then if friction is equal to mgsinq, it will not go at all. If friction is smaller, the object will accelerate down the incline because of the unbalanced force down the incline. However, if it starts in motion and friction is greater than mgsinq, it will slow down until it stops, that is until the net work done by the friction and gravity takes away the kinetic energy.

QUESTION:
So we are teaching kids about the movement of the earth around the sun. Is it the sun's gravity that keeps the earth in orbit? What gave it its initial energy to move around the sun?

ANSWER:
Yes, it is the gravitational attraction force which the sun exerts on the earth which is responsible for the earth's orbital motion. In nature, whenever there is a motion of a particle in a circle, there must be a force which points toward the center of the circle. The simplest everyday example is a ball tied to a string and moving in a circle (imagine a tetherball); the string pulls on the ball (the force) and the result is its circular motion. If you cut the string, the circular motion ceases and the ball flies off in a straight line. Depending on the level of understanding of your students, you might want to talk about Newton's second law: the result of a force is an acceleration. Then you can talk about how something which moves in a circle is accelerating even though its speed stays the same. Acceleration is the change of velocity and velocity can change either by speeding up or slowing down or by changing direction.

Regarding your second question, the earth was not created as it is with some particular orbit but accumulated over billions of years. The current understanding of planet formation is that, when a star is originally "born", most of the mass coalesces as the star because gravity pulls it together; but, because the cloud from which it formed has a little bit of spin to it, there is a disk of residual dust and rocks going around the star. These gradually, through collisions and sticking and later gravitational forces holding bigger pieces together, accumulate to form the planets, so the planets got their energy from the energy originating in the motion of the cloud of matter from which system was formed.

ANSWER:
Absolute potential energy has no meaning; only changes in energy are meaningful. If we say that the final energy is equal to the initial energy plus the amount of energy added by friction (which is, of course, negative since friction takes energy away from the object), then E_final=E_initial+W_friction. If the object is initially at rest at y=h, then this equation becomes
mv²/2=mg(h-y)-fy/sinq

QUESTION:
Hello-I am an AP physics teacher in Michigan and neither I nor my students can figure out the answer to the following puzzle. Tetherball is a game in which a ball is tied to a pole and two opposing players try to hit the ball so the rope wraps all the way around the pole. To eliminate the effects of gravity, the same game can be modeled with a hockey puck on a frictionless plane tied to a pole with a string. Here's the puzzle: According to conservation of angular momentum, as the string wraps and the radius (i.e. length of the string) decreases, the angular velocity of the puck increases. Because omega=v/r, it can be shown that V final=(Rinitial/Rfinal)V initial, hence the linear velocity also increases as the radius decreases. What is doing the work to cause this increase in KE? In the common textbook problem, a person or other "energy source" pulls the string inward, hence the person does the work, the energy coming from the food they ate. But when the rope does the pulling due to its wrapping around the pole, I can't find the source of the energy which does the work that must be done to increase the speed. All of the AP physics teachers I have asked are stumped.

ANSWER:
This is a classic introductory physics problem. Where you have gone wrong in your analysis is to assume that the angular momentum is conserved. The condition for angular momentum conservation is that there be no external torques on the body, in this case the ball. The only force (ignoring gravity) on the ball is the tension in the string. Now, since the string does not go through the axis about which you are computing angular momentum, you can see in the figure to the right that the tension (labelled F) has a component which is perpendicular to the line from the center of the pole to the ball, so it exerts a torque on the ball, so angular momentum is not conserved. Furthermore, the velocity of the ball (labelled v) is always perpendicular to the string and therefore F does no work; if there are no external forces doing work, then the energy is conserved so the kinetic energy does not change, so the speed of the ball actually remains constant in the tetherball problem.

QUESTION:
What is known about time travel?

ANSWER:
It is possible to travel into the future using time dilation, a well-known result of special relativity. This is what is known as the twin paradox (not really a paradox at all). Basically you travel to a point far away and back at a very large speed and when you return more time has passed on earth than for you so you have traveled forward in time. As far as we know, it is not possible to travel backwards in time. Read more about the twin paradox here.

QUESTION:
If a plane is traveling at the speeed of light and someone is inside the plane at the back tail end part and they run to the front of the plane, would they be traveling faster than the speed of light?

ANSWER:
Well, for starters, it is certainly not possible to travel with the speed of light because it would take an infinite amount of energy to get your plane going that fast. But suppose that went with a speed of about 99.999%, for all intents and purposes the same as the speed of light for your question. If you ran to the front of the plane with a speed of say 99% the speed of light, your speed as seen by somebody on the ground would be about 99.5% the speed of light. This is fundamental result from the theory of special relativity—nothing can go faster than the speed of light and anything with mass must have a speed less than the speed of light.

QUESTION:
My question is this. Suppose that in the far future mankind has found the means to travel with the speed of light. If we manage to send a spaceship 1.000 light years away, equipped with a extremely powerfull telescope that will be capable of looking directly to the surface of earth from that distance, will it be looking earth as it was 1000 years ago or more ( if the distance is greater )? For instance will it be capable of taking ... aerial photographs of ancient Rome etc?

ANSWER:
Well, for starters, it is certainly not possible to travel with the speed of light because it would take an infinite amount of energy to get your spaceship going that fast. But suppose that went with a speed of about 99.999%, for all intents and purposes the same as the speed of light for your question. Then you would arrive at about the same time as light being emitted from earth at the time that you left. So if you trained your super telescope back on earth, you would see things progressing starting from shortly after you left.

QUESTION:
Is it possible to speak about a "speed of darkness" or that is only the opposite of the speed of light since darkness is the absence of travelling photons?

ANSWER:
"Darkness" is not something physical and so it is rather pointless to talk about its speed. If you have a flash of light, there is a spherical shell of light expanding out from the source with the speed of light, so the back side of the flash is the edge of advancing darkness behind it, so I guess you could say that the darkness is increasing with the speed of light.

QUESTION:
I don't know why this would be of any use but, If you mounted two conductive parallel plates of large magnitude to the top of a lightning rod with the top plate suspended by an insulator and lightning struck the top plate, would that be like charging a giant capacitor?

ANSWER:
Sure, assuming that equal and opposite charge could be acquired from the ground for the lower plate. However, it would likely not happen since lightening "selects" a path where the charge can find a route to ground.

QUESTION:
If you set off a nuclear weapon in a black hole what would happen? I thought nothing because the particles would not be able to move around because of the super stong gravatational pull.

ANSWER:
You could not get a nuclear weapon into a black hole in tact.

QUESTION:
i was once concidering the effect of propelling an object backward off a moving vehicle with the exact velocity that you are travelling. From my point of view the object is moving away from me, but to an observer standing at the side of the road at the instant i throw the object it merely drops to the ground. This made me wonder if it is possible for light to behaive in the similar manner. In this hypothetical situation an object must be travelling the speed of light. Would the light from the object travelling in the opposite direction of travel merely stand still in space becoming "dead light" or would it accelaterate to it's regular pace. In this situation we would also have to assume that the object is generating it's own light since light itself would not be able to reflect off it due to it's speed.

ANSWER:
It seems like I answer this question (in various forms) at least weekly! There are two problems with your hypothesis, both violations of the theory of special relativity. First, no material object may have a speed equal to or greather than the speed of light; the reason, simply, is that to accelerate it to the speed of light you would have to supply an infinite amount of energy, obviously not available. Second, one of the basic postulates of the theory of theory of special relativity is that the speed of light in a vacuum is the same for all observers. Thus, even if your object were moving with 99.99% the speed of light (which is possible), an observer at the roadside would see the light from its back end moving with the speed of light, not 0.01% the speed of light. The theory of special relativity is completely verified experimentally and no serious scientist doubts its correctness.

QUESTION:
what would happen if a small hole was drilled right through Earth, that is from one side to another going through the Earth's core, and I so happen to drop an object into that hole, would the object fall right through, fall towards the middle and stay there, or result in a ping pong effect? (Given that the posibillty of creating such a hole is possible, without a catastrophic event happening)

ANSWER:
This is a classic introductory physics problem. The object will speed up until it gets to the center and slow down until it gets to the hole opening at the other side, will then start speeding up back toward the center, etc. If the earth is modeled as having uniform mass density (which is only roughly accurate), the motion of the object will be what we call simple harmonic motion, that is it will behave exactly as if it were attached to a giant spring.

QUESTION:
Is it possible to contruct a machine that repels gravity?

ANSWER:
I don't really know what you mean by "repels gravity". I suspect you are interested in an "antigravity" machine. The answer is yes, there are lots of antigravity machines. One is an airplane which wants to fall to the ground. Another is a tabletop which keeps a book on it from falling to the ground. I am obviously being a little facetious here. What would be neat is to have something which is repelled instead of being attracted by a gravitational field. For this to happen, there would have to be another kind of mass (just like in electrostatics we have two kinds of electric charges and so we can have both attractive and repulsive forces). As far as we know, there is only one kind of gravitational mass.

QUESTION:
what happens when parallel rays are incident on a plane mirror?

ANSWER:
The reflected rays are also parallel.

QUESTION:
The other day I was watching a child play with one of those funfair baloons, filled with (what i think is) hellium. Often children let go these ballons, and they just keep on rising and rising... My question is: how high will such a ballon rise, assuming minimal wind (i.e. if the ballon rose approx. vertically)? What if the ballon had hidrogen instead of hellium? Is it different?

ANSWER:
The reason the balloon rises is the same reason wood floats. When an object is in a fluid (like air or water) it experiences an upward force (called the buoyant force) equal in magnitude to the weight of the fluid which it displaces; this is called Archimedes' principle. So the balloon has two forces on it, its own weight down and the buoyant force up. If the weight of the air displaced by the balloon is greater than the weight of the balloon, there is a net force pushing up which will push the baloon up. This will be the case if the balloon is filled with helium but not if it is filled with water, for example. Now, the air in our atmosphere has, as you probably know, the property that it gets less and less dense as you go higher and higher; for example, it is quite hard to get enough air on top of Mt. Everest and airplanes which fly at more that a few thousand feet must be pressurized. For this reason, the buoyant force gets smaller and smaller as the balloon rises until, eventually, it is the same as the balloon's weight and it will stop rising. I have ignored, in my explanation, the fact that the balloon will get larger as it goes higher because the pressure of the gas inside stays about the same while the pressure of the air on the outside gets smaller; I think the important thing to appreciate is the Archimedes' principle thing. This is the principle which lets "lighter than air" craft (hot air balloons, blimps, etc.) fly.

QUESTION:
why can't visible light waves penetrate most solid walls, yet every frequency below and above visible light can, such as radio waves, gamma, micro, etc?

ANSWER:
You are incorrect in stating that "every frequency below and above visible light can" penetrate. Electromagnetic theory shows that there is a distance called skin depth at which any electromagnetic wave will decrease to about 1/3 of its amplitude outside the medium. For conductors the skin depth depends on the wavelength in such a way that long wavelength waves can penetrate much farther without significant loss of intensity. At the short wavelength end of the spectrum (gamma rays, for example) the usual theory breaks down because we have very energetic single photons interacting with the atoms in the material and doing such things as losing energy by ionizing atoms their its paths; here, the more energetic (i.e. shorter wavelength) the photon, the farther it will go before using up all its energy.

QUESTION:
I was taught in school that the speed of light is the speed limit of the Universe. Nothing can go faster than light. In E=MC2, the speed of light is squared. If nothing can go faster than C, why does the the equation get square C. Isn't C2 faster than C?

ANSWER:
But, this equation does not mean that something is going with a speed c². In fact, going with a speed c² does not have any meaning since speed squared would be measured in, for example, miles²/hour² which are not the units of a speed. Just because c (3x10⁸ m/s) is the fastest possible speed does not mean that c is the biggest possible number. There are, for example, many more than 3x10⁸ stars in the universe.

To see questions and answers from longer ago, link here.