Ask the Physicist!

QUESTION:
Fermilab's YouTube channel has an enlightening clarification of the phenomenon of refraction: In it Dr. Lincoln explains that charges in a material contribute their own electric waves, which combine with the incident light to form a new wave, which travels through the material at a lower speed. However, I am left with more questions. I believe that for electromagnetic radiation to interact with something, a photon must be absorbed, but his explanation expressly mentions that this does not need to happen for refraction to take place. What am I misunderstanding?

ANSWER:
This is a case where he is doing purely classical electromagnetism (EM). No photons are needed. He is giving a (qualitative) microscopic explanation about how v can be less than c in materials. It was well known in the 19th century, before quantum electrodynamics was known, the nature of electromagnetic waves. Everything you can know about EM is contained in four equations, Maxwell's equations. From these equations in a vacuum you can find a wave equation describing oscillating electric and magnetic fields and traveling with a speed c=1/√(ε₀μ₀) where ε₀is the permitivity of free space and μ₀is the permeability of free space. Anything not a vacuum is not described by these two constants but by corresponding constants ε and μ which are larger than the vacuum counterparts. Therefore the wave equation describing a EM wave has a speed v=1/√(εμ) which is always smaller than c.

Incidentally, the constants are simply constants of proportionality dependent on how you define magnitude of electric charge (usually Coulomb) or electric current (usually Ampere). For example, the force between two equal charges Q separated by a distance r can be determined experimentally to be proportional to the square of Q/r, F∝Q²/r², so F=CQ²/r². where C is a proportionality constant which contains ε₀, C=1/(4πε₀) if charge is in Coulombs.

QUESTION:
How massive does an object have to be in order for its mass to change the rate of acceleration due to gravity? And how does this fit in with F=ma and a=F/m? I understand that for small objects, acceleration doesn't change due to mass, a 1kg object and a 2kg object will fall at the same rate due to the Earth's gravity in the absence of friction. But surely there must be some change in acceleration due to mass albeit miniscule for smaller masses? If we consider 2 objects in a vacuum, in the absence of any other objects they will exert a gravitational pull on each other and fall towards each other. If one is the size of the Earth, and the other object is 1kg, that acceleration is 9.8ms^-2, but if both objects are as massive as the Earth do they accelerate towards each other at 19.6ms^-2? What if one object is the size of the Earth and the other the mass of the moon, or the Earth and the Sun?

ANSWER:
This "rule" that you are trying to apply, that two masses with different mass fall with the same acceleration, technically applies only to point masses in a uniform gravitational field. Since the gravitational field of a large sphere of radius R is approximately uniform at altitudes h«R and most objects are much smaller than the size of the earth, this rule works approximately. But if the field is not uniform (it actually falls of like 1/r² where r is the distance from the center of the earth) and/or if the objects are not small compared to the size of the earth, all bets are off. I want to keep the algebra and integrations simple, so as an example I will look at two thin sticks whose masses are uniformly distributed; one has mass M and length L, the other has mass M/2 and length L/2. The gravitational field points in the downward (negative y) direction everywhere, but decreases linearly as you move upward; so the acceleration due to this weird gravity is g=g₀(1-δ(y/L)) with g=g₀ when y=0 and g=g₀(1-δ) at y=L where δ is just a dimensionless constant which specifies how rapidly g decreases as you go upward. Note also that I have aligned the centers of mass of the two sticks so that it is a "fair race". The math is not hard but is a bit tedious, so I will just give you the final results. I find that the acceleration right now is A=-g₀(1-δ) for M and a=-g₀(1-(15/16)δ) for M/2. If δ is very small compared to 1, A≈a and if δ=0, A=a.

Your last couple of questions are meaningless because you have assumed that the acceleration due to gravity is g everwhere, but it isn't as I noted at the beginning of my answer—only very close to the surface of the earth.

QUESTION:
If I set a timer to shine a light at my space ship in 5 minutes. Then I get in my space ship and fly away at 99% the speed of light, how much time will I experience before the light reaches me? And how much time would it take for the light to reach me from the perspective of an individual location at the light source?

ANSWER:
It is more convenient to answer your second question first. You move with speed v=0.99 light minutes/minute (lm/m)* and the light moves with speed 1 lm/m, so the ship is at a position x_s=0.99x5=4.95 lm when the light turns on. Calling the time when the light turns on t=0, the equations for the ship and light front are, respectively, x_s=4.95+0.99t and x_l=t; if we set x_l=x_s, it is easy to show that t=495 m and then x=495 lm. Now we look from the your perspective (your first question). You see the 495 lm distance moving backward at a speed 0.99 lm/m so, because of length contraction, its length is x'=495√(1-.99²)=69.8 lm and the corresponding time is t'=x'/v=69.8/0.99=70.5 m.

*Sorry for the lousy notation here. The unit m here denotes minute, not meter!

QUESTION:
In a Carl Sagan video, "boy on bike with waiting brother" provides a simplistic layman explanation of the effects of light speed travel. IS IT POSSIBLE for time dilation to occur when all "subjects" (the boy, his high-speed vehicle and his writing brother) are all earthbound?

ANSWER:
First of all, it is not "light speed travel" which is impossible, speeds are close to the speed of light. As to your question, being earth-bound has nothing to do with time dilation or length contraction; only speed matters. True, the classic "twin paradox" problem has one brother flying straight out into space and straight back because it is easy to calculate analytically, but there is no reason the traveling twin couldn't just go round and round in circles before stopping.

QUESTION:
I have what I hope is a quick question that you could help me with. I'm trying to find equation(s) to chart communication across space to a spacecraft. My hypothetical spacecraft is traveling at the velocity of .1c towards a ship that is relatively static and how long communications would take as the distance between them decrease starting at .25ly.

ANSWER:
Since the gamma factor at 0.1c is 1.005, I will ignore relativistic effects. I am not sure what you mean by communications, so I assume that you mean the length of time for a message sent from the moving spacecraft to (M) to arrive at the stationary spacecraft (S) as a function of where M is. The position d of M relative to S is d=0.25-0.1t ly; the time for light to travel that distance is T=d/c where c=1 (ly/y). Therefore T=0.25-0.1t y. The graph shows this.

FOLLOWUP QUESTION:
What I meant is to find out the length between each communication between the the traveling ship and the point in which it's traveling to. For example communication with earth to ship to Mars communication basically starts at no delay and eventually time between the two is delayed as it goes to mars and decreases as it returns. How would I graph that and find out how long the delay is as the ship is moving towards i.e. Earth? [I was a little confused still about what he meant. He sent the picture which cleared it up.]

ANSWER:
What is wanted is the time, on earth (E), between when a signal is sent to and a reply received from the ship (S) as a function of the ship's distance from the earth (ESE); his sketch implies that he is also interested in the reverse, the time (SES), so I will do both. The zig-zag paths of the signals shown in the questioner's sketch form many triangles which are similar triangles; hence, if we do the geometry for one triangle it will be correct for all. The two graphs show one of these triangles for each. Three important lines are labeled by their linear equations. The quantity d is simply any arbitrary distance between S and E at the time when the communication is initiated.

It now becomes a problem of analytic geometry, in particular where linear functions intersect. In the case of ESE, d-0.1t=t so t=d/1.1; since this is an isosoles triangle, the elapsed time T for the communication is twice this, Δt=2d/1.1. It is a little trickier if communication is initiated by the ship because it isn't an isosoles triangle; still, it is easy to find the intersection of y=t-d and y=d-0.1t to be Δt=2d/1.1, exactly the same as for ESE. Finally we find that, whichever initiates the communication when S is at y=d, the total time is Δt=2d/1.1. In your case, the first communication would be when d=0.25 ly, so Δt=0.455 y=41.5 days. A communication initiated when the ship is halfway home, d=0.125 ly, would take Δt=0.227 y=83 days.

[My wife said to ask you if you are writing a sci-fi novel!]

QUESTION:
My Question is related to Fluids. When a washing machine is started(which is filled with water), water inside it, form a shape of like a tornado(which revolves around a common centre) which can be explained by effective gravity which has components- artificial gravity and normal gravity (taking that revolving water as our non-inertial frame of reference). But how can the same phenomena be explained by inertial frame of reference?

ANSWER:
I have never seen the centrifugal force called artificial gravity before, but I guess that is what you are referring to. The explanation in the inertial frame is illustrated in the diagram. The shape of the surface is a parabaloid of revolution. I will focus my attention on a tiny piece of the water on the surface. There are two forces on it, its own weight W and the force F which the surrounding water exerts on it. The horizontal and vertical components of F are shown. The vertical component must equal W and the horizontal component must be the centripetal force mRω² where ω is the angular velocity and R is the distance to the axis of rotation.

QUESTION:
Struggling with length contraction. Is it just a matter of perspective and not actually contraction? If I am on a rocket at high speed, standing and facing forward, I experience no difference in the depth of my thorax. From the perspective of a person at rest, relative to me, they see my thorax depth to have contracted. How is that physically possible? My heart and lungs cannot be infinitely compressed. Yes, I know the math can be worked out for both perspectives, but is it actually happening? It is just how the rest frame "sees" me?

ANSWER:
There are two important issues here:

How is the length of a moving object defined?
How long does a moving object appear to be relative to how long it is?

I have discussed these at great length in an earlier answer. When looking at a three-dimentional moving object the results can be surprising.

QUESTION:
I have a simple camera - a 'VP Twin' - fixed focus positive meniscus lens, aperture, shutter speed. basically 'point and click' in bright sunlight. I have become curious how it can be in focus from 8 feet to infinity. On close examination it has a curious feature - the distance from the lens to the film plane is 47 mm, but the distance from the lens to the focus of infinity is 50 mm. This is apparently impossible. So two questions, Does 1/F = 1/U + 1/V hold for positive meniscus lenses? and is the focus of infinity distance for a positive meniscus lens the focal length?

ANSWER:
The equation you have written is called the thin lens equation. You should be aware that it is only an approximation but a pretty good one. I prefer the notation 1/f=1/i+1/o where f is the focal length, i the image distance, and o the object distance. If o=∞ then clearly i=f so clearly f=50 mm. So the image for an object infinitely far away is not on the film, and that object is not perfectly in focus. So what is perfectly in focus? 1/50=1/47+1/o and solving, o=-783 mm. What does this mean? It means that there is a virtual object located 783 mm behind the lens! This is obviously not the way any simple camera works because to have a virtual object you need another lens to create it. You can easily show that for a simple converging thin lens that all images of real objects are farther behind the lens than the image of an object at infinity. So you have something certainly wrong with your numbers. If you had said that the image of the sun (focal length) is 47 mm behind the lens and the film is 50 mm behind the lens, it would have been possible: o=783 mm, a real object 7.83 cm in front of the lens. I am not going to analyze in any more detail because when I googled this camera I found that the focal length of the lens is 35 mm. I have included a plot of i as a function of o out to o=100 m (100,000 mm) for a 35 mm lens. As you can see, beyond 10 m the image is only 0.1 mm or less off the focal plane; so if you set the film a distance f from the lens, most of what you want is quite well in focus. I have read that this is what is normally done for fixed-focus cameras.

QUESTION:
If I was in free fall from a skydiving alt. And I was falling on a platform that let's say for sake of argument didn't flip over and over and instead stayed flat while falling to the earth.(let's say it was designed to fall flat on the top side) It would obviously absorb some amount of wind resistance, therefore slowing it down ever so slightly. Me as a skydiving human being standing on top of the flat platform would not have any wind resistance because it would be broke by the platform. Therefore my falling velocity would be fast than the platform. Therefore making it possible that I could walk around on said platform (again, assuming it couldn't flip over). Is that correct? Could I walk around on a falling platform because of the differential in velocity due to the air resistance the platform would undergo and not my body?

ANSWER:
Well, aerodynamics can be very complicated, so there is no guarantee that you will feel on effect from the wind, but that is not the real crux of your question so I will assume that it is true and that the platform (absent you) will maintain its horizontal orientation as it falls. To make this easier to generalize, I will have the platform be a uniform solid cylinder. What are all the forces on the platform (without you)? There is its own weight W which may be thought to act all acting at its center of mass, and there is the air drag D which would likely be distributed uniformly over its area and therefore you could treat it as a single force acting up also at the center of mass. If the mass of the disc were not uniformly distributed, the center of mass would not be at the geometrical center; the disc would not be in rotational equilibrium, there would be a net torque about the center of mass and the platform could not be as you wish it to be—remaining in a horizontal plane. This is shown in my diagram.

Now, let's add you to the mix. If you stand at the center of the disc all is well. But, if you wander off on the platform, the force you exert down will exert a torque and the disc will commence rotatating.

You refer to the effect of the drag to be "ever so slight" but the drag would be quite strong for a platform large enough for you to imagine wandering around on it. That is how a parachute works.

QUESTION:
if two objects fall at the same time with different masses, neglecting air resistance, will they fall at the same time? keep in mind that their masses are different for example one has 100kg of mass and one has 1kg of mass

ANSWER:
This is the old Galileo experiment, famous even though it probably never happened! If there is no air drag, any object will fall with the same acceleration and therefore both will always be falling side by side; see the experiment performed with a feather and a hammer by an astronaut on the moon where there is negligible air. And, if you know Newton's first law it is not hard to understand:

The only force on a falling object with no air drag is its own weight which is its mass times the constant g which is a constant which tells you how strong the gravity is; on the surface of the earth, g=9.8 m/s². Newton's second law says that the force is equal to the mass times the acceleration. So, F=ma=mg and a=g; no matter what the mass is, it acceleration is always equal to g.

You might be interested the case when there is drag. The drag force depends roughly on the size and shape of the object and the square of its speed. So, for example, if you drop two spheres of the same radius but one has a mass m and the other has a larger mass M, at any given speed v each will experience the same force because the force does not depend on the mass. Newton's second law will be F=ma=mg-cv² where c is just some constant which carries all the information about size, shape, gravity strength, air density, etc. (The minus sign is because the weight is a force down but the drag is a force up. So a=g-[cv²/m] and similarly A=g-[cv²/M] for the more massive ball. In your example, M=100 kg and m=1 kg, a=g-cv² whereas A=g-0.01cv²for the 100 kg mass, much bigger. The heavier wins.

QUESTION:
What grants authority to biological materials to alter matter through DNA? If all matter was created at the emergence of the universe, how does DNA, plant and animal life, allow for growth and create structures that did not previously exist?

ANSWER:
The first thing you should understand is that all energy was created when the universe began, not all matter; matter is just a form of energy. In elementary chemistry we are taught a principle called conservation of mass. In fact, this "law" is only approximately true; what is true is conservation of energy, that mass can be created or destroyed as long as the total energy is conserved. For example, when methane is burned by combining it with oxygen, we get carbon dioxide and water; energy is released in the form of heat so the mass after the burning is actually less than before. Chenmistry, however, is a very inefficient way to get energy because the change in mass is extremely tiny which is why the law of mass conservation was, for centuries, believed to be true because the instruments were not accurate enough to detect such small changes. Biology is just a collections of natural machines which do chemistry. For example, a plant takes energy from the sun to to create sugar and growth by chemically manipulating water, air, and minerals.

QUESTION:
My twin brother and I are here on earth in the same reference frame. We are both 20 years old. He then travels in a rocket at 0.87c for the next ten years. He then returns to earth. I am now 30 years old. IS HE ONLY 25 TEARS OLD?

ANSWER:
You should read my earlier answer about the twin paradox; if you looked on the faq page you could have linked to it. But I will work it out for you. If I understand your question, your brother travels to some distance d for five years and then back in five years. Since his speed is 0.87c, the distance to his destination is d=vt=0.87*5=4.35 light years (ly). Now, because of length contraction, he sees the distance he travels out to be d'=4.35√(1-0.87²)= 2.14 ly. Therefore, according to his clocks, he has traveled not 10 years but 4.28 years and is thus 24.28 years old.

QUESTION:
Why are particles waves and not spirals? I feel like I can't imagine a particle going in a zigzag motion as opposed to it rotating around.

ANSWER:
You never try to talk about what the "particle part" is doing when you are talking about the "wave part". Take light, for example. We have know since the 18th cetury that light is a wave. In the 20th century we found that it is also a particle which we call a photon. You, as you seem to feel, would not imagine photons zig-zagging over the crests of the wave. For the electron, for example, the wave we envision is a wave which specifies the probability of finding the electron particle at some spot in space, not a physical wave in space.

QUESTION:
When/where can matter and anti-matter pairs form? Can this only happen in a vacuum? Also, since matter and anti-matter both have mass, how can the Law of Conservation of Mass not be violated when these pairs are created?

ANSWER:
I will talk only about photon creation of electron-positron pairs. It can only happen if the photon energy is equal to or greater than twice the rest mass energy of an electron; otherwise energy could not be conserved. It cannot happen in a perfect vacuum because the participation of another particle, usually a nucleus, is required for the reaction to be able to conserve linear momentum. Other particle-antiparticle pairs would have similar restrictions. There is no such thing as conservation of mass, just conservation of energy; mass is, afterall, just a form of energy. Conservation of mass is a useful approximation for elementary chemistry, but it is false in detail; e.g., the mass of a water molecule is not equal to the mass of an oxygen atom plus the mass of a hydrogen atom plus the mass of a hydrogen atom. The difference is small but not zero.

QUESTION:
A person is standing on a tower say three meters above a swimming pool. The pool is on the deck of a moving boat that is moving in the same direction as I am facing. The speed although not really important is say five knots. Now, let's say I jump off of the tower and successfully enter the water. Is there a point or height of the tower where the length of travel or time of fall that would be such that the pool would eventually move out from underneath me and I would hit the tower? I would be in straight free fall and the platform is moving. I assume that gravity would eventually stop all forward momentum causing the fall to plumb to the earth. If the target is moving to an unattached platform underneath me, it would eventually have to move out from underneath me, correct? Given a long enough fall/time?

ANSWER:
For starters, the speed actually may be important, but let me come back to that. First, let me neglect air drag. When you step off the tower you, like the boat, are moving forward at 5 knots. Now, the only force on you when you are falling is your own weight which accelerates you vertically; there is no force horizontally so you continue to move forward, right along with the boat so, no matter how high the tower is, you will land directly on the spot in the pool you were directly over when you jumped.

Now, if air drag is considered, it is as if you were falling but a v_w=5 knot=2.57 wind were blowing you horizontally so you would be accelerated backwards from the direction of the boat. So, I have worked out the answer to how far, given the numbers you have specified: you will fall* from 3 m in 0.78 s and you will be pushed backward about 7 mm and have acquired a speed of about 2 cm/s. Not much effect.

Finally, for anyone interested I will give an outline of the calculation I did but not all the detailed steps. To estimate the air drag at sea level I like to use the approximation F=¼Av² where A is the area pushed on by the moving air and v is the speed of the air relative to the object; in this case, v should be replaced by (v_w-v) where v_w is the speed of the wind and v is the horizontal speed of the jumper, so

F=¼A(v_w-v)²=ma=m(dv/dt).

(It is important to note that this approximation only works if you use SI units.) This can now be integrated to find the horizontal velocity of the jumper as a function of time,

v=tv_w/(k+t)=dx/dt where k=4m/v_wA.

This is plotted for v_w=2.57 m/s (5 knots), m=68 kg (150 lb), A=1 m² in the first two figures above. Note that for very large times (first figure) the velocity approaches the wind speed as you would expect. The second figure shows very small times; the time to fall is about 0.78 s (see footnote*). Finally, integrate the v equation to find the distance traveled horizontally as a function of time:

x=v_w(t+klog(k/(k+t))) where log is the natural logarithm.

The position x is shown in the third figure. For very large t this curve will increase linearly with a slope of 2.57 m/s. I haven't worked it out for other conditions, but the distance traveled horizontally could be made larger for larger v_w, larger h or smaller m.

*Assuming that the person is jumping or diving straight down, there will be little air drag going down. The required time to drop to the ground from a height h can be shown to be v=√(2g/h) which is 0.78 s for h=3 m.

QUESTION:
I used to think it was really amazing the way a clock run slower due to higher acceleration or gravitational fields. The more I thought about it it doesn't seem that weird because they would be dragged on the hands of the clock. Can you explain to me how something greater than that is happening and that it is actually time that's slowing down?

ANSWER:
Your way of understanding time dilation is certainly off the wall! What if the gravity were so strong that it crushed the clock so that it stopped completely? Would time stop completely? It would probably useful to you to first understand time dilation in special relativity; time (as you measure it) in a frame of reference which is simply moving relative to you with constant speed runs more slowly. You must accept that the speed of light is constant to all observers; then you can easily use a "light clock" to understand.

QUESTION:
I am curious to why mechanical advantage works. I understand how pulleys offer mechanical advantage. I understand the math. I do not understand why there appears to be a mechanism in physics that allows the translation of weight into length of rope.

ANSWER:
I am not sure what you mean by "translation of weight into length of rope". To understand what is happening you need to know Newton's three laws. Let's consider the simplest example I can think of with a pulley, weight, and rope. The first of the three figures shows the situation: a rope is attached to the ceiling, passes over a pulley, the other end pulled up by you, and a weight W is supported by a rope attached to the axle of the pulley; everything is at rest. If the force which you pull up with is less than the weight, then there is mechanical advantage. The physics concepts you need are Newton's first and third laws. The first law says that if an object is at rest, all the forces on it must add up to zero; the third law says that if one object exerts a force on another, then the other exerts an equal and opposite on the the first.

To solve this problem it is best to focus on one object at a time; first, focus on the weight as shown in the second figure. There are two forces on the weight, its own weight W which points straight and the rope which exerts an upward force whose magnitude I will call T₁. (I think we can agree that a rope is capable of exerting a force and this force is usually called the tension. There is no weight being "translated" to the rope, rather the rope is just exerting a force on the weight.) So now the first law tells us that T₁-W=0 or T₁=W. You are not holding up this weight and the pulley is not holding up this weight, this piece of rope is. Next, focus on the pulley. There are three forces on the pulley the tensions on the left, right, and certer as shown in the third figure. You are not pulling the pulley, the rope is; the ceiling is not pulling the pulley, the rope is; the weight is not pulling down on the pulley, the rope is. Now we need to use the third law: T₁ pulls up on the weight so the weight pulls down on the rope with a force of magnitude T₁; the rope is at rest so the pulley must be pulling up on it with a force of magnitude T₁; therefore the rope is pulling down on the pulley with a force of magnitude T₁ which just happens to be equal to the weight; the weight is not pulling down on the pulley. The other two forces on the pulley, labelled T₂ and T₃, must be equal in magnitude or the torque they exerted would make the pulley rotate. So, now, we can apply the first law to the pulley and find 2T₂-T₁=0 or T₂=W/2. Finally we can use third laws arguments like we did for the hanging rope to deduce that you must use a force W/2 to hold up a weight W. I know this must seem pedantic to you, but when you are first learning this kind of problem it is important to understand which forces are exerted on something to avoid fuzzy thinking like the weight being translated to the rope.

QUESTION:
I know the equation of intensity follows as I = S / 4πr² How is this equation derived and what are the base formulas in terms of the inverse square law.

ANSWER:
Technically, this is the intensity for a point source or sources which are spheres. So let's assume that a point radiator is emitting a total power S which is energy per unit time. A point source will radiate energy isotropically, i.e., uniformly in all directions. Intensity is the power per unit area passing throught an area A. The area through which the energy passes is A=4πr² where r is the radius of any sphere with the source at its center, so I=S/(4πr²). There is your derivation. As I said, this is only exactly true outside of spherically symmetric sources, but most sources look like a point source if you are far enough away. The units of intensity are Joules/second/meter squared (J/s/m²) and J/s is a Watt (W).

QUESTION:
In regards to the effect of dark matter on galaxy rotation, would get the same results by assuming a larger gravity effect exerted by the galaxy's central black hole?

ANSWER:
I normally do not answer questions which are astronomy/astrophysics/cosmology. In this case though, I think I can answer. There is no way that the folks who do this kind of calculation would not have included the effects of supermassive black holes.

QUESTION:
I have been thinking about Einstein's formula E equals MC squared. I can understand where Einstein got his notion of mass and energy what escapes me is the speed of light squared. What clue did Einstein have That indicated the speed of light should be squared why not just the speed of light or why not the speed of light to the power of three or 10. What indicated that the speed of light squared should be used and what pointed Einstein in this direction.

ANSWER:
I have gotten this question before and it shows that you do not understand the way we specify units in science. To take an example you can understand, suppose that you are traveling in a car with a speed of 57 miles per hour; if I asked you how fast you were going and you said "57 pounds" we would both know it was nonsense. In the SI system of units scientists usually use, energy has the units of kilograms per meter squared per second squared (kg/m²/s²) and this is called a Joule (J). As you see, mc² has those units and mc³for example, does not. (A more familiar unit to you may be the unit for power, the rate at which energy is created or consumed, is the Watt (W) which is one Joule per second (J/s)). This is not the only misconception in your question, but also understanding how theoretical physics is done. A new theory generally starts with a very few suppositions and then the theorist works out what the implications of those suppositions are on physics. In the case of special relativity the suppositions are that the laws of physics are the same in any frame of reference and that the speed of light is the same for all observers. What these two postulates lead to are many new understandings of physics and one of them is that E=mc². You may be sure that Einstein didn't sit around thinking and suddenly a lightbulb flashed over his head and he went "Eureka, E=mc²!"

QUESTION:
My dad was driving in a highway, when we leave the highway there is a banked road. When car turning right, my body is leaning to the left. I thought my body will lean to the center due to centripetal force. Why??

ANSWER:
Newton's laws do not work in accelerating systems. When you are turning the direction of your velocity is changing and so you have an acceleration even if the speed is constant; this acceleration, as you probably know, points toward the center of the circle you are turning and has a magnitude v²/R where R is the radius of the circle and v is your speed. But in your frame you are at rest, not accelerating at all. If you are leaning on a door on the outside of the turn, you feel the door pushing you. That is a force but, since your frame is at rest, you have an unbalanced force but your acceleration is zero. Your brain, however, feels that push and interprets as you are being pushed by some mysterious force against the door making you feel like you are being pushed to the left. That force does not really exist even though you feel like it does. But this is all understood if viewed by a pedestrian observing you: she sees the door pushing you toward the center of the circle providing the observed acceleration. The real force is the force (centripetal) of the door on you, the force (centrifugal) you think you feel does not exist and is usually referred to as a fictitious force.

QUESTION:
I am writing a fiction piece that includes a carrousel space station (a la 2001) and have two questions about the positioning and orientation of said station. This would be a 200 meter diameter I think.
First - I intend that the space station will not be geostationary (35000km out) but want it to be semi geosynchronous. That is, I would have it circle the earth once every 180 min as opposed to the ISS 90 min). I presume it would higher than the 400km to slow the revolution. At what height would that be?
Second, I was wondering what would the optimum axis or rotation for a 100 to 200 meter diameter station? Axis parallel to the line of gravity? (I.E. the if it were on the surface it would spin like a top) Axis in line with the orbit? (the station disc is aligned more or less N-S ) Axis perpendicular to the orbit and the line of gravity (so if it were on the surface it would roll like a wheel)

ANSWER:
Kepler's third law states that the square of the period T of a circular orbit is proportional to the cube of the radius r of that orbit, T²∝ r³. Keep in mind that you have specified the altitudes h of orbits, not their radii where r=R_E+h and R_E=6378 km is the radius of the earth. So now you can write (T₉₀/T₁₈₀)²=(r₁/r₂)³=¼. You can now solve for r₂, the radius of the orbit for the 180 minute period, r₂=1.59r₁=1.59(6378+400)=10,778 km. You can express this as an altitude, h₂=4399 km. For your second question you need to realize that the spinning station has an angular momentum (which points along its axis of rotation) which remains the same if there is no net torque on the station which there should not be, at least to an excellent approximation. Therefore if you try to orient the axis either radially or tangentially it will soon not be pointing in that direction since the angular momentum vector would have to change but it won't; e.g., if you set it radially or tangentially it will be pointing tangentially or radially after having gone a quarter of the way around its orbit. If normal to the plane of the orbit, it would always be that. On the other hand, I can think of no good reason why the orientation would make any difference. You might be interested in an earlier answer and links in it which discuss these rotating space stations in detail.

FOLLOWUP QUESTION:
I get your visualization of the station starting off radially aligned becoming tangential after a quarter revolution, but am thinking that would only happen if the station itself was spinning like a flipped coin counter to the revolution. If the station were aligned axis tangential and canted slightly might it possibly give itself angular momentum and propel itself around the orbit - like the spinning bicycle wheel in the hands of a person standing on a lazy susan.?

ANSWER:
Your space station is rotating as shown in the picture. Its angular momentum points along the axis of rotation. Now, there is an external force on this station, the gravitational field, but this force exerts no net torque; gravity exerts a force which causes a torque due to each piece of the station, but for each piece there is a piece on the other side which exerts an equal but opposite torque. Newton's first law says that if there is no external torque, the angular momentum will be unchanged no matter how the station moves around. There is no angular momentum corresponding to a "flipped coin" rotation unless you exert a torque to get it rotating like that, and you would never do such a thing. The second figure shows what I was talking about in the first answer: with no external torque angular momentum direction does not change as you go around the orbit.

Your speculation about the satellite "propelling itself" is totally wrong. No propulsion is ever required for a satellite because it is in free fall and just continues falling. Also the bike wheel-stool-person example is irrevelent because it is not analagous. It is also an angular momentum conservation example but because an internal torque (by the person) changes the angular momentum of the wheel, the person acquires an angular momentum of her own to keep the total angular momentum the same.

QUESTION:
Why doesn't an irregular or polygon shaped hole work like a pinhole camera when held at or close to the screen? It requires some distance between the hole and the screen to make an image. When a card with a hole of any shape is held close to the screen, the lighted area on screen is of the same shape as the hole. To make an image of light source, say Sun, the card has to be moved away from the screen to get an image. Why does it not show the image in the first case? I want to understand the path of light rays for the two situations and the transition. The explanations for the simple pinhole with rays going through the hole to make an image are shown for small holes; but any size hole works as camera lens at sufficient distance. I'm unable to use that explanation and ray diagram for the above question of large hole near and far away from screen. If I think of a larger hole as made from several small pinholes, even then how do i explain that larger hole close to screen gives a sharp image/shadow the same shape as hole and makes the image of light source as distance to screen is increased?

ANSWER:

I have shown above the photographs taken by the questioner showing the results for the pinholes both near to and far from the screen; The object supposedly creating the image is the sun. A pinhole is imagined as a hole with infintesmally small size; of course, such a hole would let in no light at all, so we have to have a hole which is very small compared to the distance to the screen. No pinhole camera is perfect, but we can fabricate one which is very small indeed. So now I show in the next diagram ray diagrams for two pinholes and the resulting images they form of the arrow.

The one on the left is so small that only one ray from each point on the object can get through the hole thereby forming a nice sharp image. On the right the hole is much bigger so that now the rays which can get through are many, those between the two rays shown coming from each end. I have shown images made by these extreme rays but there will be a continuum of such images and the net effect will be an image which is only barely recognizable as the the image of the object, a total blur. You cannot even call my second example a pinhole camera because its size is not small compared to the distance to the screen. Your reason for expecting a sharp image from a big hole, because a lens is a big hole, is totally incorrect. The reason is that the purpose of the lens is to bend the light rays so that all the rays from any point on the object end up at the same point on the screen.

QUESTION:
My friend thinks the reason a spaceship would reach infinite mass if it achieved the speed of light is because an infinite amount of fuel would be needed to supply the energy. I disagree. Is he correct? I hope not because it would mean I don't have the grasp on the psychics of this situation that I think I do, which is one have notch above the pure layman.

ANSWER:
Your friend has the right idea. Any object with mass which is traveling at the speed of light has an infinite total energy. Therefore, to get the mass to that speed you need to supply an infinite amount of energy. But our entire universe does not contain an infinite amount of energy.

QUESTION:
This is is a question relating to music, specifically piano music. There is a lot of misunderstanding among pianists about the physics of how sound is produced. Basically, the volume of sound produced by striking a piano key is a function of the speed of the hammer as it strikes the string. But, assuming you strike the key three times, and in each case the hammer is traveling at the same speed on impact, is the volume of sound the same, whether the hammer is accelerating, decelerating, or at a constant speed on impact?

ANSWER:
I started off answering your question by acknowledging that a piano is a very complicated system, but still trying to do some simple analysis of your question making simplifying assumptions. As I was plowing forward, I was simultaneously doing research since I knew little about the mechanisms of a piano. What I discovered is that your question involves situations which cannot occur in real piano. The hammer comes up to the strings from below so that it will fall back down when the strings are struck. But, an essential component of the hammer mechanism is that the hammer is released from the mechanism connecting it with the key just before it strikes the strings; the mechanism which causes this to happen is called the escapement. Therefore, your question is moot because the hammer is moving freely when it hits the strings and, because the only force on it as it approaches the strings is its own weight, it is slowing down. If you want an excellent introduction to the physics of the piano, a talk given by Professor Nick Giordano of Purdue University at Georgia Tech. (Unfortunately, this video is slightly out of focus but still worth watching.)

QUESTION:
Can a bolt/Arc of electricity be affected by a wave of kinetic energy such as an explosion’s blast wave. I’m not looking for any real world application this is for a fiction book I am writing. The only reason I refer to an explosion is because I can’t think of another example close enough to what I mean.

ANSWER:
A spark is just the break down of a gas which occurs if there is a strong enough electric field. Free electrons in the gas are accelerated by the field and they collide with molecules which results in more electrons and the positive ions they leave behind. So a current will be created through the previously insulating gas. So, if you disturb the air, it will certainly affect the way this spark forms.

QUESTION:
I've been under the impression that if 2 objects of the same shape and size but different weight are dropped they will fall at the same speed. I've seen videos and articles also proving this. However my father and I conducted a test with a piece of steel 3x1x1 inches and a piece of wood 3x1x1 inches. Neither weigh that much probably less than a pound each. When dropped the steel always hits the groumd first. I know it must deal with air resistance some how but they have the same surface area so I can't figure out why the steel falls first.

ANSWER:
You are certainly right that it is air drag which causes this to happen. And you also note that they have the same area but you don't say what that has to do with anything. Let's just write down a general expression for the drag force, f=½ρCAv² where ρ is the air density, C is a constant determined only by the shape and orientation of the object, A is the area presented to the onrushing air, and v is the speed of the object. So, you see, the drag force on the steel is identical to the drag force on the wood. But what matters is not so much the force on the object but rather the effect this force has. The net force on an object with mass m is f-mg and, using Newton's second law, ma=f-mg; so a=f/m-g. So, you see, the larger the mass, the smaller the effect in slowing down the falling object. There would have been a much more dramatic difference if you had fashioned a 1x1x3 box out of paper.

QUESTION:
Do rotating bodies have to be a finite distance from the center of rotation to move? Consider a circular pad of sand grains. Any line drawn from the edge to the center will have interlocking sand grains. If there is one grain at the exact center it must rotate to make the whole pad move. But the grain has molecules and atoms and etc. There has to be an exact center (R=0). The rotation formulas fall apart with zero radius. Rotation can occur if there is no rigidity.

ANSWER:
To be clear here, we are talking about classical Newtonian physics where such a thing as a point or a point mask are assumed to exist, even though they don't (except maybe black holes which are not part of classical physics). A point, having no size at all, cannot rotate about an axis which passes through it. So a point mass at the axis of rotation of some rotating rigid body has neither a velocity nor rotational velocity. You mention a "grain"; thinking of a spherical grain of radius r for simplicity, if its center is located on the axis of rotation neither it nor any other point on the axis is moving, but all other points are. If you think of the the central point as an atom or radius r, the same arguments apply, but classical physics is not applicable to objects as small as an atom. I do not know what you are talking about that "The rotation formulas fall apart with zero radius"— v=rω so v=0 if r=0.

QUESTION:
If you have a light source that is emitting a constant number of visible red photons per unit time as seen by an observer that is stationary relative to the light source and then the observer starts moving towards the light source at, say, 99% the speed of light, what exactly would the observer experience? I presume one would see the photons very strongly blue shifted, maybe even to the point of becoming gamma rays?? Maybe killing the observer because of the ionizing radiation?? Also since the observer is moving into a continuous stream of photons traveling away from the source at the speed of light, would brightness (the number of photons per unit area per second) of the source increase? To the point of vaporizing the observer? Or what if the observer was moving perpendicular to the light source at a very high speed, would it intercept a much larger quantity of photons moving away from the light source and thus make the source somehow appear much brighter although not be blue shifted?

ANSWER:
The first part of your question is called the relativistic longitudinal Doppler shift and is easy to calculate: λ'=λ√[(1-β)/(1+β)] where β=v/c. In your case, β=0.99 so the blue shift is λ'=0.071λ. So, suppose that we take λ=700 nm; then λ'=49.7 nm, at the low-energy end of vacuum ultraviolet, probably not energetic enough to kill the observer and pretty easy to shield against. For the case of light coming from a source not directly ahead, you can see the math in the Wikepedia article on relativistic Doppler shift.

More interesting to me though is the effect on all the stars all around me when I am going at a very high speed. Their apparent positions all tend to collapse into a very small-angle cone directly in front of me. Hence, I would find it almost impossible to navagate and would have a very intense of high-intensity, high-energy radiation coming directly at me. See an earlier answer.

QUESTION:
Scientists are saying a nova 1286 LY away will nova, if so won't it be 1286 years before we can see it on earth do telescopes shorten the time. The reports I see act like when the nova occurs we will see it at that time

ANSWER:
If it is 1286 light years away, anything we see of it will have happened 1286 years ago, telescope or not. So if those scientists say that it will happen soon, that is what our clock will say, but the actual event happened a little more than 1286 years ago.

QUESTION:
My mother says one radiator is better than another at heating our house. But I think it's only insulation that makes a difference. Because hot air can't just "disappear" because your radiator is made of one thing rather than another or has a shelf above it.

ANSWER:
If the two radiators are identical, their effectiveness depends only on their environments. One aspect would be the rate at which heat escapes the room; it is not only insulation, but also windows, doors, etc. Also, the radiator in a small closet would keep you toasty warm but not in the astrodome, so volume of the room being heated is also important.

QUESTION:
if you replace a 100 watt incandescent light with a led light using much less wattage that has the same amount of lumens will the output on a solar cell (on your calculator) be the same?

ANSWER:
I once answered a question which delved into the definition of a lumen and its relation to other units of electromagnetic wave energy, power, etc. which you might be interested in.

To answer your question, though, you have to look into the spectrum of emitted light of your two bulbs and the spectral response of the solar cell. I have included two figures above, one showing the the spectra of the sun, a typical led, an incandescent bulb, and a cfl lamp. The visible spectrum is about 350-750 nm (0.35-0.75 μm). Note that the led is taylored to having nearly all of its radiation in the visible range, whereas the incandescent bulb is most intense in the red and infrared range (long wavelengths). But, as the spectral response of the solar cell figure shows, the cell is most responsive in the long-wavelength regime. Therefore, your calculator battery will charge faster with an incandescent bulb than an led bulb.

QUESTION:
I am 72 years old and not a crank, yet. Cannot get answer to simple query: How much energy is in ONE electromagnetic wave of any particular wave length, say one radio wave? I know the usual equations such as energy-h*frequency. I cannot see how to make them work with one wave alone. I am good at algebra and OK at calculus. I know waves rarely come alone but usually come as part of photons. Still, waves do have a distinct identity when traveling, at least ideally. I have self-studied physics.

ANSWER:
Unless you are talking about a single photon, there is no such thing as "…ONE electromagnetic wave". In a classical electromagnetic wave there are rays and wave fronts. The way to specify the energy depends on the particular wave. Electric and magnetic fields have energy densities (the amount of energy in a volume divided by the volume) associated with them. But an electromagnetic wave has constanty changing fields so the energy density will be constantly changing and we are generally more interested in the time averaged energy density. Also, though, a wave has a flow of energy away from the source; This flow is generally expressed by a quantity called the Poynting vector S, the units of which are watts per square meter. An example is a plane wave in a vacuum, a wave in which wave fronts are planes. Here S=|E|²/Z₀ where Z₀=√(μ₀/ε₀) is the impedance of free space and E is the electric field. The time average value of the poynting vector is <S>=<|E|²>/Z₀=E₀²/(2Z₀) where E₀ is the maximum magnitude of the electric field. So, you see, it is a complicated situation.

QUESTION:
Is building a time machine physically possible

ANSWER:
It is possible to travel to the future but not the past. We already have time machines; your car, for example, moves you forward in time when you make a round trip but since the speed of a car is so small compared to the speed of light you never notice it. For example, suppose that you travel at 60 mph for an hour and then return at the same speed.

QUESTION:
What will happen to the momentum of raindrops as it falls yo the ground

ANSWER:
Any object falling through air will experience a downward force (its own weight) which will speed it up as it falls. But, when it starts moving it also experiences an upward force due to air drag which increases as speed increases. Eventually the drag force up becomes equal to the weight force down, so it then falls with constant speed until it hits the ground. The drag force depends on the size (hence on its mass) and shape of the raindrop as it falls. Because it is deformable, it will change its shape as it falls, so to compute its speed as a function of time would be a very complicated problem to do in detail.

QUESTION:
Can megnetic fields exist independently of electric charges?

ANSWER:
All electromagnetic fields ultimately depend the source of the fields, electric charges. Magnetic fields may be caused by electric currents in a wire which has no net charge, but the electrons in the wire are moving which is the cause. Magnetic fields are also caused by an electric field which is changing, but you ultimately had to have electric charges to cause that changing electric field.

QUESTION:
what happens when sound waves are produced in a chamber with diminished air molecules. I'm a musician and am considering experimenting with vacuum chambers and hand held percussion instruments while recording to try to capture some unique sounds. I know sound will not travel through a vacuum, but I am wondering about the effect of a space with a diminished level of oxygen molecules.

ANSWER:
The speed of sound c in a gas, which is what is going to determine how a musical instrument will sound, is given by the Newton-LaPlace equation, c=√(K/ρ) where K is the bulk modulus of air and ρ is the density. If you remove air from some volume you are reducing the density, so it would appear that the speed gets larger as you remove air; however, K depends on temperature and pressure, so you need to dig deeper to find out what c is because if you take air out the pressure is going to decrease. You are probably not interested in all the details*, so I will just give you the final results: in dry air at a temperature T in °C, the speed is approximately c=20.05√(T+273.14). Since you will probably do your experimentations at constant temperature, the speed of sound and therefore the musical behavior will likely not change significantly.

*If you want to see details, see the Wikepedia article on the speed of sound.

QUESTION:
Does light impart any kinetic energy? Put another way, with enough light can you move an object?

ANSWER:
Light carries linear momentum and can therefore exert a force on whatever it strikes. So, yes, light can move an object. Using the sun's light to propel spacecraft has been suggested.

QUESTION:
I am a junior high school student and I would like to know how a black body will develop if it is given a continuous injection of power? Does the mass get bigger?

ANSWER:
There is a simple answer here and it does not require that we are talking about a black body. Everything radiates energy at some rate which depends on its temperature, size, shape, composition, etc. If you add energy at a rate greater than the rate it is emitting radiation, it will gain energy (most likely by increasing temperature); if the input energy is at a smaller rate, the object will lose energy but at a rate smaller than it would have if you hadn't injected energy. The mass of an object depends on its total energy (E=mc²), so increasing energy means increasing mass. In most cases, the mass increase would be unmeasurably small.

QUESTION:
Diatomic hydrogen becomes monatomic upon absorption into palladium-from whence comes the energy to separate the atoms?

ANSWER:
You are right, it takes energy to separate the atoms in molecular hydrogen. But when palladium absorbs hydrogen, a single hydrogen atom is bound in the crystaline structure of the metal. Since the H atom in the palladium is more strongly bound than it would be if bound to another H atom, the system will reduce its total energy by breaking the H₂ bond and forming the Pd-H bond. The answer is that the Pd is the source of the energy to separate the H₂.

QUESTION:
This question is about strobe lights and smoke/fire. I lit a small clump (1"x1") of pine sap on fire and put my strobe flashlight up to it to see if there was any visual effect. Instead, I heard a buzzing sound coming from the smoke. The closer I got to where the smoke was forming the louder the sound. If I increased the brightness of the flashlight the sound also got louder. If I brought the strobe to around 10 flashes a second I could hear 10 small blips of sound a second. If I covered the light the sound went away, so the sound was not coming from my flashlight.

ANSWER:
At the outset I will admit that I really do not know for sure. I did a little research and came up with some information and some ideas. The ideas I have are based on speculation, but I think they are pretty sound. I find that a typical pulse power is several kilowatts. Now, that pulse has a significant infrared component. Going through air, this does not have much heating effect because the air is pretty transparent. When the pulse hits the smoke the infrared is pretty strongly absorbed and superheats the gas which expands rapidly making a pop.

QUESTION:
How can the electrons in an antenna simultaneously oscillate an many different frequencies and modulations presented to it by electromagnetic spectrum.

ANSWER:
An electron oscillates because it is responding to a force due to an oscillating electric field. Because of the superposition principle, the fact that if two different oscillating electric fields with different frequencies are applied at one point in space, the new electric field there is simply the sum of the two at that point and time. So the electrons will behave in the same way. The figure shows this for two sine waves, one with frequency 10 times larger and amplitude 5 times smaller than the other, added together. Now, an antenna will see hundreds of frequencies falling on it; in order to be useful, e.g. for tuning a radio, you need to have an electronic circuit which filters out all but the desired frequency.

QUESTION:
This Autumn here in the UK (like many other countries) the clocks went back an hour. Everyone talks about the clocks going back and 'gaining' an hour. But surely, didn't time move forward? I clearly understand time in this sense doesn't actually move forward or backward as it is just our measurement of it. But.... the clocks may have gone back, but time has been brought forward not backward surely? For instance. On the 30th of October the Sun will have set here at around 17:30. But the 31st it now sets at 16:30. Time has not gone 'back' as it were, we have in fact moved time 'forward'. The sunset has been brought forward in this sense. The clocks go backward....but time is brought forward?

ANSWER:
In any frame of reference (e.g. the UK), time proceeds forward at a constant rate. So we need some operational definition of how to measure time intervals, the time elapsed between two events. Pretty universally used is the second (s). (I will not go into how the second is measured, but you know what it is. Now, when we do a physics problem which involves time, the first thing we do is to choose some time where the time has a value of zero; all later times are positive and earlier times are negative for this choice of t=0. In your case, t=0 could be midnight. Then 1:00 AM would be t=3600 s. Imagine that you go to sleep at 1:00 according to this clock. Now, suppose the British government decrees that midnight will henceforth occur when your clock reads 11:00 PM. According to the government's choice of t=0, you go to bed at t=0 s, midnight. But, just as in your sunset example, your going to bed is an event that happens at a particular time regardless of how you label it (according to your choice of t=0).

QUESTION:
Because of drag, a human-made satellite needs occasional rocket thrusts to stay in its orbit, otherwise it will fall to earth. Why does not the earth experience drag from its OWN atmosphere, and fall to the sun? Similarly, why does not the moon experience drag from its OWN atmosphere, and fall to earth?

ANSWER:
Not all satellites experience significant drag because if their orbits are far from the surface of the earth there is virtually no air. The earth's atmosphere rotates with the earth and therefore there is no drag. You might argue that if there is a wind it is rotating at a different speed; but I would guess that you looked at all the winds on the earth there would be just as many speeding up the earth's rotation as slowing it down. In any case, even if the atmosphere did cause a drag it would change the rotational speed, not the orbital speed. The moon has no atmosphere and is well outside the earth's atmosphere, so it experiences no drag. There are drag forces on the moon and earth due to the tides which the moon causes; see an earlier answer.

QUESTION:
I'm attempting to calculate the velocity of an object over time given air resistance and am not finding an equation online. The force from air resistance is 1/2 v^2 x d x A x cp where d is the density of air, A is the area of the object and cp is a constant given the geometry of the object's surface area. If an object weighs 10 kg and is traveling at 10 m/s in a 0 gravity environment with an area and cp both set to a value of 1 then the air resistance or drag on the object is 61.25 N. Dividing by the mass of the object and multiplying by an incremental change in time of 1 second is a change in velocity of 6.125 m/s. The object's velocity after 1 second is 3.875. Each calculation for velocity requires the previously changed velocity. After 2 seconds the velocity is 2.955 m/s and 3 seconds is 2.42 m/s. If I draw a graph with time on the x axis and velocity on the y axis is there a function F(x) to calculate velocity given time and the initial velocity?

ANSWER:
Yes, there certainly is. You should realize that what you did is a reasonable calculation but that since the velocity is constantly changing, it is not very accurate to assume that v stays the same over 1 second. What you are doing is the first step in calculating the integral of the quantity but you need to find how it improves as you make the time interval smaller and smaller. Since you ask this question, I assume that you have had no calculus; therefore you will probably not understand the following derivation. Do not lose heart, the function you seek will emerge at the end! First, I usually use the approximation that, at sea level, the drag equation may be approximated

F=-¼Av²=Ma=M(dv/dt)

where M is the mass of the object, A is the area it presents to the onrushing air, and a is its acceleration; the minus sign signifies that the drag force is opposite the direction of the velocity. [It is important that this equation is not dimensionally correct and will only work using SI units.] So, we can write that

dt=(-¼A/M)^-1v^-²dv.=(-4M/A)v^-²dv

Integrating from t=0 to t, v(0)=v₀ to v(t)=v and then doing a little algegbra, I find

v=v₀/(1+kt) where k=¼Av₀/M.

For example, the graph for v₀=20 m/s and k=1 s^-1 is shown. The constant k is just whatever the coefficient of v² in the force is divided by the mass. You could use your value, for example, k=½dAC_pv₀/M.

QUESTION:
I was thinking about light sails.. if I take a photon, with energy = hf , obviously that is the energy of the photon. Then we have this photon momentum : p= hλ. If I have 1 photon of light and I make it incident up on a free floating stationary mass with no external forces upon it that is mirrored such that the photon is reflected and a certain proportion of its energy is transferred to kinetic energy on the mass it is incident upon.. and then I repeat the experiment but this time I make this photon incident upon a metal first with a very small work-function such that it liberates an electron, fully transferring all its photon energy into both liberation and the kinetic energy of that election.. and then that electron collides with our original free floating stationary target mentioned earlier.. would either the first case or the second case impart more momentum to the object in question (I know some energy would be used to liberate the electron, but would more of the photon energy be transferred to kinetic energy)?

ANSWER:
(The momentum of a photon is h/λ, not hλ.) Let's look at the first situation first. Before the collision the energy of the photon is e=hf, and its momentum is p=h/λ=hf/c; the sail has E=P=0. Assuming an elastic collision, after the collision the photon has a momentum (approximately) of p'=-hf/c so momentum conservation gives us that p=p'+P' or P'=2hf/c. But the mass (M) is macroscopic and moving very slowly, so P'=Mv where v is its speed; so v=2hf/(Mc) and E'=½Mv²=(2/M)(hf/c)².

Next you propose that we use the photoelectron created by the photon to collide with sail. The energy of that electron will be E=hf-W where W is the work function. If we assume that the electron bounces back just like the photon of energy hf did, it will have less momentum to transfer so the recoil and hence the resulting kinetic energy of the sail will be smaller.

QUESTION:
I'm a retired saxophone player who likes to play bongos on a paddleboard, on Lake Michigan. It was my understanding that any for any resonance chamber, the pitch is higher for a shorter tube, and lower for a longer tube. But when I set the bongos on the paddleboard, resting on their lug nuts, there is about 3 cm space between the bottom of the drum shell and the surface of the paddleboard, where water can wash underneath the drum during a big wave. And the pitch goes down. Isn't the water underneath effectively making the drum smaller? Shouldn't the pitch go up?

ANSWER:
Actually, the main thing that is happening is that you are changing an open pipe to a closed pipe; the shortening of the length is a negligible effect on the pitch compared to the closing off of the end. In the figure above I have sketched in the vibrating drum head in red for the two kinds of situations. The right end of the drum must be an antinode where the air is vibrating its maximum amount because that is where the drum is beating on the air. The "open ended pipe" is the situation when the bottom of your drum is open to the outside air; because the air there is totally free to move, that is also where there must be an antinode of the resonant wave. The fundamental tone is then the lowest-pitched wave which can fit in there and, as you can see, it is one half of a full wave. When the water comes up it closes the previously open end and keeps the air from vibrating there, thus becoming a node. Now the lowest pitch which can fit is a quarter wave, a longer wavelength and therefore a lower pitch than the open ended pipe.

QUESTION:
Hi, regarding superposition of nuclear particles, it is said the electron (for example) exists in a superposition of states (all states at once) until it is measured (momentum, spin etc) and this measurement colapses the "probability wave". The probability wave as i understand it, is not a real thing, it's a graph showing where the electron is most likely to be in space. Now my ripe with it, isn't it rich to assume that an object exists in all possible states before being measured ? My nighbour, i haven't seen him today, does that mean he's everywhere else on the planet until i go check his house? I understand he's not a quantum object but still, this superpostion assumption is to me really far fetched unless i can be show actual evidence of something being in two places at once.

ANSWER:
You are confusing "superposition" with "probability wave"; they are actually different things. For example, an electron can have two possible spin states, either up or down; sometimes the electron will be have a little amount of each, like 60% up and 40% down and a measurement of the spin of that electron would be more likely to find the spin up than down. Although not really a good example, your neighbor's superposition is that his state has zero probability anywhere than in his house. A probability wave is essentially the square of the wave function of a particle or system of particles; the wave function has no direct physical meaning until it is squared. The resulting probability distribution does have physical meaning in that it tells you that if you look in one particular place you will have some particular probability of finding it. If you look at a cloud in the sky, do you say that it is in more places than one just because it is spread over some volume? Think of your electron as a cloud; it is not in many places at the same time, rather it is just spread out. The electron cloud is different from the cloud-in-the-sky cloud because if you make a measurement of some place inside the sky cloud, the whole cloud is not suddenly there.

QUESTION:
I understand that a light year is a measurement of distance, but aren't the time and distance interchangeable? For example, if I'm looking at a star that is 10 million light years away that means that I'm effectively seeing that start 10 million years in the past, correct?

ANSWER:
I would not say that time and distance are interchangeable, but the distance light travels in a certain time is a good measure of distance because the speed of light is a universal constant. But you wouldn't say that the time it took for a car to go from New York to Miami was interchangeable with the distance between the two cities. Indeed, as you suggest, when you look at the stars you are looking into the past because of the time it takes their light to arrive.

QUESTION:
Do sub atomic particles exist or just a theory?

ANSWER:
Yes, they exist. Very few are stable but those which are unstable play an important role in the interactions between particles. Nearly all have been observed directly in experiments. A few, quarks in particular, are unobservable directly but predictions assuming that they exist have been so successful that they either exist as particles or else they provide a very accurate description of how nature works.

QUESTION:
Since soundwaves can create heat, and the louder the soundwave is, more heat is created, does pitch affect how much heat is created as well?

ANSWER:
The energy carried by a wave is proportional to the square of its amplitude but does not depend on its frequency.

QUESTION:
Has Heisenberg's uncertainty principle being proven either right or wrong? or is it still under experimentation?

ANSWER:
The HUP is one of the keystone components of the theory of quantum mechanics. It posits that the observable quantities, position and linear momentum, are not independent things but actually coupled; if you change one of them it has an effect on the other. (Mathematically, in the theory, each is the Fourier transform of the other). These are called conjugate variables and the result is that the more accurately you measure one, the less accurately you can know the other. The proof that it is correct is that quantum mechanics has never failed to correctly describe the properties of very small systems like atoms. So everytime you find that some physical system (e.g. the structure of some atom) is well-described by quantum mechanics, you are proving the HUP. See a recent question very much like yours.

QUESTION:
Can a force cause

a moving object to accelerate,
a moving object to rest, and
a resting object to move.

I just want to know the science it was a test question and I got it wrong and I kind of want to know.I

ANSWER:
Force (F, a vector) causes a mass m to accelerate (a, a vector) as indicated by Newton's second law, F=ma. Acceleration is the rate of change of velocity (v, a vector). A vector can change in two ways, it can either change its magnitude (speed up or slow down) or change its direction; all three of your situations are the result of changing the magnitude of the velocity. We could have had a fourth situation:

a moving object to move with a constant speed.

If an object moves in a circle with constant speed (the speed is the magnitude of the velocity vector), there must be a force which is always perpendicular to the direction of the velocity vector. An example is a planet moving in a circular orbit around a star where the force is the gravitational attraction to the star.

QUESTION:
I was recently working through some practice problems for a mechanics course that I am enrolled in. The current unit we are covering is work and power. One question asked us to find the power required for a mass (.119 kg) to accelerate from 0 m/s to 27 m/s in 0.36 sec. I thought that you could find the acceleration using the kinematics formula 'V = Vo + at' to solve for acceleration; and then use the formula 'P = m*a*v' to solve for power. When I looked at the answer key, this was not the way that they solved the problem. They used 'P = W/t' where 'W' was the change in KE. I can understand why this approach is correct, however, I was puzzled as to why the answer that I got solving it my way was exactly 2x greater than the one found using their method? I have been thinking about this for a while now, but unfortunately am having no luck.

ANSWER:
v(t)=v₀+at gives you the velocity at some time t if the acceleration (and hence the force) is constant; but you have no idea whether that is the case. The equation you used, P=Fv is not applicable if v is changing which it surely is. However, it will work if you use the average velocity over the time interval. Since you have assumed that a is constant, v is increasing linearly and so v_average=½v(t=T) where T is 0.36 s in your case. There is your factor of 2!

QUESTION:
Is quantum uncertainty intrinsic to physical reality or a measure of our ignorance??

ANSWER::
Both. If the uncertainty principle is correctly stated, it is a correct physical principle which indicates the degree to how well you can possibly know something. It does not say that no quantity can be known to arbitrary accuracy. But if you have two quantities and they are what is calledd conjugate variables, then it is not possible to know both of them to arbitrary precision. For example, position and linear momentum of an electron are conjugate variables. If you form the product of the uncertainty of each, it cannot be smaller than approximately the rationalized Planck constant, ℏ. So the more accurately you try to determine the position of the particle, the less you can know about the momentum; conversely, the more accurately you try to measure the momentum of the particle, the less you can know about its position. If you were to know exactly what the momentum is, you would know absolutely nothing about where that particle is, could be anywhere in the universe! A second example of a conjugate pair is time and energy. So suppose you have a stable atom of masss M in its ground state; you may measure its energy E=Mc²to any degree of accuracy you wish because you have an inifinte amount of time to do so. But if the atom is excited to some excited state of energy E+E', it will decay back to the ground state and so you only have a short time to measure its energy. Thus the energy of that state is not exactly E' but actually broadened by some amount determined by the half life of the decay; the shorter the half life, the more uncertain the energy of that state is.

QUESTION::
My step dad is adamant that you could put a wind turbine on a car that will help charge the battery on the car to make it go further or help recharge the battery. Afaik this doesn’t work due to perpetual motion and this is similar to that drawing of a fan trying to blow its own sail. That thermodynamics wouldn’t allow enough of a wind turbine or a “fan” he says that soaks up the wind that the car produces(which I think is just air resistance so not enough energy) to make this idea viable. Am I correct it wouldn’t work or is there someway we could use a fan to produce electricity on a car to recharge the battery or help battery last longer etc??

ANSWER::
Well, your stepfather is right. Driving through still air the turbine will be able to charge the battery, but dead wrong that this will make the car go farther. Where does the energy sent to the battery come from? The forward motion of the car lets there be a wind which will spin the propeller. But the car needs the energy to keep it moving with a constant speed. Since the turbine is removing energy from the moving car, the car needs to provide more energy to keep moving. So the energy that goes into the battery is supplied by the engine. In the real world there is friction and other energy losses in the turbine, so the net effect is for the whole car to lose energy..

QUESTION::
Gravity waves propagate at the speed of light. We know this because of very sensitive lasers. How can any phenomenon that is hypothetically faster than light be measured by something that is not, for example photons? Wouldn't everything measured always be at the speed of light or less??

ANSWER::
Actually, the speed of gravity has not been measured. In general relativity it is assumed that the speed is the speed of light and nothing has indicated that it isn't. The most convincing evidence that I am aware of does come from the laser-interference measurements. Although most of the events detected are from black hole collisions, one was a collision between neutron stars. A collision between black holes should be unobservable with conventional telescopes because no light, xrays, gamma rays etc.can escape. However the neutron stars collision was observed by telescopes at just about the same time; given the enormous distance away of the event, the speeds of light and gravity must be very close..

If you look at my site ground rules, you will see that I do not answer questions about faster than light speeds because physics-as-we-know-it forbids that happening..

QUESTION::
How does speed affect our aging? I have read on the internet that the faster you go, the slower you age. I'm just wondering how can time affect the biological aging of a person. I also watched the twin paradox video wherein the guy who traveled near the speed of time looks younger than his twin who stayed on earth. Does that mean our biological process of aging that happens inside and outside our body gets affected by our speed??

ANSWER::
You should first readd my explanationnof the twin paradox. For the traveling twin the time proceeds for him just as it would if he had stayed at home. But the distance he has to travel before turning around becomes shorter. The earth-bound traveler observes his brother's clock running more slowly. Regarding aging, if you think about it, the body is essentially a clock; average age about 80 years, average time between heartbeats about 1 second, for example. The earth-bound twin observes all clocks on his brother's space ship slow down, including his brother's body clock..

QUESTION::
I recently thought about why I can see a smaller object than reality reflected when a hold an pen in front of a spoon? Normally I think the object should look bigger because the surfaces of the spoon is bended inwards and some of the areas outside the real pen in the spoon should also reflect the pen. Is it something wrong with my spoon??

ANSWER::
I think from your question that you have not studied geometric optics. So I will give a very brief tutorial here. First of all, the thing which you call "reality", the pen, is referred to as the object. The reflection from the mirror which you refer to as an object is referred to as the image. A spool is approximately a bowl shaped like a part of a sphere and the kind of image you will get will depend whether you look into the inside of this bowl (called a concave spherical mirror) or into the backside (convex)..

A spherical mirror has what is called a principle axis which passes through the center of the mirror perpendicular to the surface. The sphere has a radiuss Rand halfway from the surface to the center of the sphere on the axis is a point called the focal point ((F). Light coming in parallel to thee principlee axis is reflected out through the focal point;; Light coming in through the focal point is reflected out parallel to the principle axis. Above are diagrams for the concave mirror showing the geometry and a ray diagram for an object placed farther away thann Rfrom the spoon which will certainly be the case for the spoon you are looking at. Note that the image is smaller than the object (just as you found) and inverted. The image is called a real image because it is on the side as the object and could be seen on a screen placed there..

If you happen to be looking at the back of the spoon you have a convex mirror. Above are shown diagrams of the geometry and ray diagram for this situation. Here rays coming in parallel are reflected directly away fromm Fand rays coming in directly att Fare reflected parallel to the principal axis. Now the image is again smaller but now upright. This is called a virtual image because it is not really where you see it to be; if you put a screen behind the spoon you would not see the image there..

I have used some images from the Wikepediaa articleeon curved mirrors. I have added (in red) rays which come in towardd F. You can learn a lot more detail there..

QUESTION::
The hydrogen material in a thermonuclear device is supposedly compressed into helium by the force of the X-rays produced by the detonation of the fission component of the weapon. X-rays are photons. Particle physics shows that photons are massless. How can something that has no mass compress anything??

ANSWER::
Even though a photon has no mass, it does have linear momentum. The reason for this is that at high velocities (the speed of light is the highest possible), linear momentum is not mass times velocity. If it has linear momentum, it can exert a force.Even though a photon has no mass, it does have linear momentum. The reason for this is that at high velocities (the speed of light is the highest possible), linear momentum is not mass times velocity. If it has linear momentum, it can exert a force.

QUESTION:
Say I have one cannon that it is free to roll backwards due to recoil when I fire it, and I have another that is secured very firmly, and cannot freely roll backwards due to recoil. Will the more secured cannon that cannot freely roll back and forth give the cannonball more energy than the one that can freely roll if given the same amount of powder and the same mass of ball?

ANSWER:
I will discuss this assuming that the cannon fires horizonally and that the ground is horizontal. You can also do the problem if the cannon ball is fired with some vertical component of its velocity, but the details obscure understanding the concepts. The total energy created by the explosion (call it E) must be divided up between the kinetic energies (K_m=½mv² for the cannonball and K_M=½MV² for the cannon) of the cannonball and the cannon; this is called energy conservation. The amount of energy each gets is determined by the velocity each has after firing; this is found by applying momentum conservation which says the amount of momentum before firing must equal the momentum after firing, linear momentum being defined as mass times velocity. Since momentum is zero before (both with zero velocity), 0=mv-MV or v=MV/m. (The minus sign is because the cannon recoils in the negative direction.) For example, suppose the masses are equal; then v=V and each will then have half the energy. Or if the cannon were 100 times heavier than the cannonball, v=100V, so the ratio of energies is (½(0.01M)(100V)²/½MV²)=100. Finally, lock the cannon to the ground; now, M is the mass of the whole earth. So, since the mass of the earth is so much larger than m, let's just call it infinity and the cannonball gets all the energy.

QUESTION:
"the physics definition recognizes that sound exists independently of an individual’s reception." I don't agree with this. surely they should be referred to as compression waves? They only become sound when they are detected by the ear

ANSWER:
This is purely a case of semantics. It is just fine to call sound waves compression waves, but in physics sound waves are defined to be longitudinal compression waves in some material. If you don't want to call it sound unless it is detected by the human ear, be my guest, but that is not physics. In addition, you definition of sound wave should probably include the compression waves being interpreted by the brain to be sound?

QUESTION:
if the earth is rotating at roughly 792 mph at the equator why dont cars need to travel faster than that in the same direction to go any distance?

ANSWER:
Because the car is already going 792 mph when it is still relative to the earth. So is the air if there is no wind.

QUESTION:
Is a photon's size less than a planck length?

ANSWER:
A photon has no well-defined size. Because of the uncertainty principle, the "size" depends on how well you know its "color". For example, suppose you have a laser whose color you know rather precisely; then the size of a photon would probably be bigger than a house. On the other hand, if you know quite precisely where the photon is, you will be able to know almost nothing about its color.

QUESTION:
Good day, this question is posed from the view of physics as a branch of science which has it's own structure, a structure that can be built on and adjusted if need be. I have looked for an obvious start to physics as a whole structure but I haven't found one that has a "start to finish" approach. It always looks as though there is underlying disorder and there is no obvious way to go about studying physics structurally. If you can, please suggest a particular structure in which physics should be studied such that no context is left haphazardly intertwined with another and every context can be derived from the previous without having to dwell at all on other related contexts.

ANSWER:
Your question assumes that the structure of physics is linear, each step a new step and based solely on what went before. But this is not how physics is actually structured. Relations among the principles of physics are complex; in fact, understanding how all of physics is constructed from its numerous components is a key goal, "unification". Your need to have no intertwining among various concepts of physics is impossible to satisfy. In my opinion, any discipline is pretty uninteresting if it can be explained using the constraints you seek. An additional problem with understanding physics is that it is not just a bunch of equations, but it is two-pronged, both theory and experiment; in fact most physicists consider observation as the fundamental source of knowledge, theory being the attempt to systematize what we observe.

In my opinion, the best way to study physics is from a historical perspective, the way the discipline actually progressed. An excellent example is the study of electromagnitism. Ancients had observed electric and magnetic forces in nature. Mainly in the 18th and 19th centuries many investigators quantified these forces (Coulomb's law and Ampere's law, e.g.) but then, in 1820, Ørsted discovered that the two forces were "intertwined" as you wish not to be. By the end of the 19th century Maxwell compressed all that was known about classical electromagnetism to four equations. And Maxwell's equations also allowed classical physics to understand a long-debated question—what is light composed of—dragging optics into this intertwinedness (just made that word up!) But all this then led Einstein to discover relativity which resulted in a revision of Newtonian mechanics, dragging in even more intertwinedness! But then, in the early 20th century, quantum physics started to be discovered and developed which led to the issue that light also has particle-like properties which means that quantum mechanics and electromagnetism had to become intertwined! It was not until the mid 20th century when Feynman and others developed quantum electrodynamics (QED), intertwining the whole set of theories into a single theory.

QUESTION:
Does negative energy exist? I have looked online and found that one article said no, then another from less than a year later says yes. I can not seem to be able to find a absolute answer.

ANSWER:
First of all, you need to know that the absolute amount of energy in any closed system is arbritrary to an additive constant; if you say some system has 6 joules of energy and I say it has 5 joules, we are both right and would arrive at the same conclusions based on laws of physics. The laws of physics do not care about the absolute value of the energy. Of course, some forms of energy you would probably want to be positive definite; kinetic energy, the energy by virtue of its motion of an object with speed v and mass m, ½mv², and rest mass energy, mc²,are always positive because m, v², and c² are. Negative energy is used all the time in various field theories. Potential energy is the best example. A planet of mass m is orbiting a star of mass M with a circular orbit of radius R; its potential energy is -MmG/R+constant and we choose the constant to be zero so the potential energy will be zero at R=∞. Similarly, the mass energy mc²of a nucleus comprised of N neutrons and Z protons but it is smaller than the total mass energies of its constiuents: mc²<Nm_neutronc²+Zm_protonc². The difference is negative and called the binding energy.

QUESTION:
Is the human body a form of energy? We have heat and electrical impulses. If so, would this not be breaking the first law of thermodynamics in that energy cannot be created or destroyed? A person is created in the womb, or is this just a transfer of energy from the mother?

ANSWER:
The first law of thermodynamics is simply the principle of energy conservation. This law states that the total energy of an isolated system cannot change. Any body with mass has lots of energy, E=mc²; and there is a lot of chemistry going on in your body, and lots electrical impulses, so if we put the body into a box filled with air where nothing can come into or go out of the box, all the energy in the box will constantly be shifting from one form to another, but if you measure the total energy at any time it will always be the same. The baby in the womb gets the energy from the mother who would usually get it from eating food, no longer available inside the box. The woman would pretty soon use up all the air, converting into mostly carbon dioxide and die. But the total energy in the box will always be the same. You know, that is the problem with conservation principles—you have to know the conditions under which the principle is obeyed.

QUESTION:
Hi, how do I calculate the force (joules) required to maintain an object in motion's speed with earth's gravity? ex.: how much force do I need to apply to a tennis ball to keep it going at a constant speed?

ANSWER:
(In the diagrams below, red vectors are forces you do not exert, green vectors are forces you exert, and blue indicates the velocity (not a force) at this instant.) The Joule is a unit of energy, not force. Force is measured in Newtons* in SI units or pounds in Imperial units. Newton's first law tells that if the sum of all forces on an object is zero that it will move in a straight line with constant speed. The forces on an object moving in a uniform gravitational field with some velocity v at some particular time is (neglecting air drag) is simply its weight W, a force straight down. So if you wish to exert a force F so that the object continues with that same velocity, you must exert a force straight up but with the same magnitude as the weight. This is shown in the first diagram and the baseball will continue moving in the direction as the blue arrow and the speed will not change; if you did not exert F, the ball would follow the arc we are used to seeing baseballs move in. If there is an air drag D (which always points in the direction opposite the velocity) as shown in the second figure, you must also exert a force d which is equal and opposite to D; also shown is the net force you could exert which is just the sum F+d.

*a Joule is a Newton·meter

QUESTION:
I'll form my question as a statement: correct or not correct. I am trying to get a grip on the centripetal, centrifugal, and Coriolis forces, particularly as regards the creation of effective gravity by rotation. An object in a rotating drum on earth experiences an apparent force (centrifugal) as the surface of the drum moves continuously into the object's inertial path of motion. A stationary object placed inside a rotating drum in space (that is to say, outside any significant gravitation) would sit in place and not move. This would be true whatever the distance is between the object and the drum (excepting some amount of electromagnetic effect depending on the composition of the two things). If however, the object contacted the drum, the object would gradually begin moving with the drum as the apparent force between the two increases. Is this correct? This was motivated by an article in Medium magazine which has been circulated widely by fellow nerds, asserting that (what was in the article misattributed to centripetal force) the coriolis force on people in this situation would make it difficult to to move, their blood to flow properly, their inner ear, etc. I.e. it can't work. Clearly this would have something to do with the relationship of the size of the drum to the person. Ok, an additional question. Look for a June 2 article at allanmlees59.medium.com

ANSWER:
I have previously answered questions like yours in great detail. See the faq page.

QUESTION:
I've googled several variations of the question: What would happen if neutrinos suddenly disappeared? The most frequent Google answers pertain research possibilities that physicists would be deprived of. But of course, what I really want to know is how it would affect physical interactions in the universe and life on earth. In short: in what ways are we dependent on neutrinos to the extent that, if they were to suddenly disappear, but with no negative effects to solar nuclear fusion, how would humans, earth, and the universe be adversely impacted? What good do neutrinos do for us now?

ANSWER:
I can think of two possible ways to interpret your question:

what if all the current neutrinos were to suddenly disappear? and
what if neutrinos did not exist at all?

I believe that the answer to the first question is that it would not change much at all. Neutrinos interact extremely weakly with matter; it was decades after neutrinos were hypothesized before they were directly observed. And, although they were originally thought to have zero mass, they are now known to have a small mass; it would take about six million neutrinos to make the mass of one electron. Still, the universe has huge numbers of neutrinos flying around and their mass could have significant effects on the dynamics of galaxies, for example. As you probably know, the universe seems to have about six times more mass than we can see; this unobserved mass is called dark matter. Could dark matter be neutrinos? Estimates indicate that only about 1% of dark matter could be neutrinos.

The answer to the second question is that neutrinos play a crucial role in β-decay and β-decay plays a crucial role in the workings of stars; so without neutrinos the universe as we know it could not exist at all.

QUESTION:
I would like to know if present physical science has the answer to, ,'why does the attractive force between two bodies diminish in the order one by d square?' The answer, 'according to Newton's equation...' is not the expected answer. Why should it decrease if space is absolutely vacuum? If there is no answer I have, based on a new space concept. If satisfactory answer is already there I had better stop my philosophy.

ANSWER:
It is helpful to envision the light from a very small (point) source. In some time t, the light carries a certain amount energy (E) away from the source with a power of P=E/t which is usually measured in Watts. Now, the total power at some distance d from the source must remain the same because of energy conservation. Now, intensity of light is essentially the power per unit area, Watts per square meter; since the area of a sphere is of radius d is 4πd², the intensity of the light falls off proportionally to 1/d². The behavior of a force field (gravity in your case) follows exactly the same arguments except we talk about the flux (field stength/area/time) and, again, the area a sphere increases quadratically with the radius. In a nutshell, I guess you could say that the 1/d² behavior is because clasically the geometry of the universe is Euclidian.

QUESTION:
My question if that a hand-sized metal ball (assuming it would not disintegrate) was propelled to the limit of the area of Earth's gravitational pull, how long would it take for this object to come back to earth. This question was inspired by the idea that if an indestructible baseball could be hit this far how long would it take to reach the Earth again.

ANSWER:

The gravitational force which an object with mass m experiences a distance r from the earth's center is F=MmG/r² where G is the universal gravitational constant and M is the mass of the earth. Note that the force never becomes zero so "… the area of Earth's gravitational pull…" is everywhere. You have to get infinitely far away from the earth for there to be no force. There is a speed, v_e called the escape velocity, which is the minimum speed which will project an object from the surface of the earth so that it will never return: v_e=√(2GM/R)=11.2 km/s=25,020 mph; R is the radius of the earth. So the answer to your question is "forever".

QUESTION:
Sir in our earlier classes we are told that gravity comes from the centre of masses but it's the Newtons theory right, but einstein's general theory of relativity that is proved to be correct, is that gravity is due to the curvature of space - time fabric and therefore masses get attracted towards each other due to slop in the curvature of warped space - time then what is true if Albert Einstein's theory is correct than gravity emerging from the centre of masses is wrong, because both theories are way different!! Even though the curvature is indused due to masses there's no point in gravitational force from the centre So why were we told in our 9th class textbooks that gravity comes from the centre??

ANSWER:
First of all, gravity does not come "from the centre of masses", it comes from everywhere in that mass. If the object is spherically symmetric, the net force always points directly to the geometrical center of the mass which is also the center of mass; this is not true for a mass with an arbitrary shape and mass distribution. I guess your 9th grade textbooks only talked about spherical objects like the earth and moon and sun for simplicity. Newton's theory of gravity is mainly empirical; he showed that Kepler's three laws for the motions of the solar system could be perfectly understood if the force of gravity falls off like 1/r² where r is the distance from the center of the sun to the center of a planet; this was a monumental achievement, based mainly on experimental observations of the planets. One of the main reasons that Newton had to invent calculus was to prove that the gravitational force outside a spherical mass was the same as if the whole sphere were a point mass with the same mass as the sphere. This is a wonderful and astonishingly accurate theory which is easy to calculate with. Nearly all calculations for celestial mechanics can be done perfectly accurately and are used on a daly basis by astronomers.

So now Einstein comes along and says to himself that this is how gravity works, but why is the force the way it is? He invents general relativity and says that this wonderful theory of Newton's is correct because the presence of mass warps space-time. Admitedly, general relativity gives some new insights as well, things like light being bent by gravity, black holes, gravitational waves, etc., but that doesn't mean Newtonian gravity is incorrect.

Calculations using general relativity are, unlike for Newtonian gravity, generally difficult to do because the calculations involve extremely advanced mathematics like Riemannian geomtry. It would be foolhearty to simply dump the classical gravity theory in favor of general relativity because then nobody but advanced graduate students would be able to understand, in any quantitative way, how the solar system works. You were taught about gravity the right way.

QUESTION:
When I fill up water jugs in the tub I put a wet towel around a bodywash or shampoo bottle so I can set the jug under the faucet with a funnel and it won't slide as the jug fills. Is there a specific law or laws to that whole process? I took physics in high school and got an A but I'm 40 now and 20 years of bartending in lol...

ANSWER:
The thing which keeps anything from sliding is friction. All you are doing when you insert the cloth between the bottle and the tub is increasing the friction. The equation for frictional forces is f=μN where f is the fictional force, N is the normal force between the object and the surface it rests on, and μ is the coefficient of static friction. If you long to harken back to high school physics, here is some more detail. If an object is on an incline of angle θ, its weight W is doing two things as shown by its two components: N is trying to press the object through the surface of the incline and D is trying to push the object down the incline. So, to hold it on the incline there must be a force the same magnitude as D which points up the incline; that would be the friction. Trigonometry tells us that D=Wsinθ and N=Wcosθ. Therefore Wsinθ=Wμcosθ or μ=tanθ ; notice that μ does not depend on the weight. For example, suppose that θ=5⁰; then μ=0.09. Suppose that μ=0.05 for your bottle sitting on the tub; then it will slide. But suppose the towel has μ=0.13 when in contact with the tub; the bottle, if sitting on towel, will not slide.

QUESTION:
So Muons have a tiny mount of mass right? And we accelerate them to near the speed of light in particle accelerators right? And the faster something goes the more mass it has, until it hits infinite which is why we can't get it all the way to the seed of light right? Assuming I am correct above, doesn't that mean if we wanted to say create artificial gravity on a space ship, we could accelerate a single Muon until it's moving so fast that it has the gravity equivalent of earth? Could this also be used to warp space and create a warp drive essentially? Wouldn't it create like a spiral gravity field that moves around the acceleration track with the Muon? Wouldn't this create some kind of gyroscopic gravity effect? If you could stop it and start the acceleration it seems like it would start causing near by objects to accelerate towards it and then past it. Likewise if the Muon keep being accelerated closer to the speed of light maybe it would enter it's own gravity wake which would be warped, and thus allowing it to accelerate faster then the speed of light?

ANSWER:
Your idea will not work for many reasons. First, look at an answer to an earlier question very much like yours; the muon is so tiny, even at huge speeds it still only gets more massive by like a few hundred thousand times, and ends up still tiny. Also, the muon is not stable and although time dilation would cause it to live much longer than if at rest, it would still only live a few seconds. Also, how are you going to accelerate it to such great speeds. Also, if you could get it massive enough so that the field would be equal to earth's at say 20 m away, the field at 10 m would be 4 times bigger.

FOLLOWUP QUESTION:
So You mentioned the field would be bigger, does that mean that the particle would get larger as it moves faster? I'm not sure I understand what you mean by that. I guess I assumed the particle would stay the same size, but act gravitationally as if it was larger. I guess if it actually has to grow to the size of earth it would not be useful. Then the other challenge is energy, I agree that's a limiting factor, if energy wasn't a barrier could it still be used to produce 1G, or would the particle become earth sized?

ANSWER:
The field being larger means the force you would feel is larger, not the size of the particle is larger.

QUESTION:
Cool, thanks! So If I can get for all the energy needed I got artificial gravity figured out ??

ANSWER:
You have obviously not read my answers carefully. The most important reason that your idea for artificial gravity will not work is that the source is a point mass and the field falls of quadratically This means that force you will feel will only be what it would be on earth if you were one distance from the particle; move closer and it gets bigger fast, move farther and it gets smaller fast. What you need is to have a uniform gravitational field, which means that the force you feel should be the same everywhere like it is on the earth. Furthermore, how are you going to keep this particle inside your ship if it is moving, for all intents and purposes, at the speed of light? Just for the heck of it, let's figure out how big the mass M of your particle would have to be for the force on a mass m a distance 10 meters from M is equal to mg where g=9.8 m/s² is the acceleration due to gravity on earth.

mg=MmG/r², so,

M=gr²/G=9.8X10²/6.67x10^-11=1.5x10¹⁴ kg

Here G is Newton's universal gravitation constant. If you were 1 m away from this mass, the force on you would 100 times your weight. The very presence of a mass this large would likely result in the collapse of the entire ship. The energy you would have to give a proton would be about 10³¹ Joules; it would take all the power plants on earth about 100 billion years (much longer than the current age of the universe) to deliver this much energy. Please do not tell me that you have "artificial gravity figured out"!

QUESTION:
Hello! I'm coming without a question about Mariana Trench. Since it's so deep and pressure is so strong, would it be possible for a £2 coin to fall to the very bottom of it? And would it be transformed in any way?

ANSWER:
A coin and water are both essentially incompressible; in other words, the coin and the water both will have the same density at the bottom as at the surface. The only forces (ignoring drag if it is moving) on the coin are its own weight and the buoyant force which is equal the the weight of the water with the same volume as the coin. So the motion of the coin does not depend on the depth and it will fall to the bottom because its weight is greater than the weight of the displaced water.

QUESTION:
The weak force is stronger than gravity. Bosons reportedly mediate or generate the weak force. Wiki says that "the high masses of bosons limit the range of the weak interaction". Perhaps the reason this seems odd to me is because I'm conceiving the weak force to function similarly the way gravity functions. Looking at it from that perspective, the greater the mass of an object, the greater its gravitational pull, right? So, if the weak force is stronger than gravity, why would the greater mass of bosons limit the range of the weak force? Or perhaps what I should be asking is: how does the function of the weak force differ from that of gravity?

ANSWER:
I should first warn you that it is very difficult to compare gravity with any of the other three fundamental forces because it is the "odd guy out"; our best theory of gravity is general relativity and the associated field has never been quantized while the others have. Therefore, it is not really possible talk about the gravity in any quantum-mechanical detail because we do not have any gravitational boson mediator to compare. However, it is generally agreed that we should call this (unobserved, unpredicted) boson a graviton. I will answer your question assuming gravitons do exist, so you should be wary.

Let's first talk about the electromagnetic force. The boson which mediates this force is the photon and it has zero mass. The electrostatic force is proportional to 1/r² where r is the distance between a point electric charge and where the force is felt. All indications are that gravity is also a 1/r² force and that gravitational waves travel at the speed of light which would mean that the graviton is also massless. It is also thought that the gluon has approximately zero mass whereas, as you note, the bosons associated with the weak interaction are massive. So, you see, the mass of the boson has nothing to do with the relative strength of the force.

The range of the force is not the same as the strength of the force. The mechanism in field theory for force is that "virtual bosons" act as mediators. But of course, these bosons have energy so if one of them suddenly pops into existence, doesn't this violate energy conservation? Yes it does! The way this can happen is via the uncertainty principle which permits a change in energy ΔE as long as it only does so for a limited time Δt where ΔEΔt ≈ℏ where ℏ is the rationalized Planck constant. So a massless boson has only its kinetic energy and travels with the speed of light, c; a massive boson has its rest mass energy as well as its kinetic energy and must travel with speeds smaller than c so it will exist for a shorter time and the range of the force will be therefore be smaller.

Finally, the only reason gravity, the weakest of all, is the only one we are normally aware of is that there just happen to be huge chunks of mass, the source of gravity, around us.

QUESTION:
I'm trying to get a handle on particle "spin". Most of my sources say that scientists long ago gave up the notion that particles actually spin on an axis the way the earth does. Wiki depicts it as a 720 degree rotation. https://en.wikipedia.org/wiki/Spin-%C2%BD Then other sources say that the spins of bosons, electrons, nuclei (and the quarks contained therein) are not the same spin. And then there's the 1/2 spin, etc. So what makes spin a spin?

ANSWER:
I suggest you look at three earlier answers, 1, 2, 3.

QUESTION:
i am trying to invent something. a tank of water, six inches deep, 20 feet in diameter. 157 cu ft. Tank rotates 60 rpm, 62 fps. What psi does outer wall have on it?

ANSWER:
There is no single answer because the pressure in a fluid in a gravitational field depends on the depth. Also, note that it will take some time for the whole volume to come to the same angular velocity, i.e. rotate as a rigid body. Now, there is an important effect which will occur when you start the tank spinning: a centrifugal force will push the water away from the axis and the surface will become parabolic in shape. Unless the tank has walls higher than the depth of the water, the water will spill out over the top. Your proposed angular velocity is pretty large (1 revolution/second) and this will make the problem extremely difficult to do. This is illustrated by using an equation which I found which expresses the the height h above the fluid in the center and upper edge of the water at the wall of the tank as a function of the angular frequency ω and the radius R of the cylinder, h=ω²R²/(2g) where g is the acceleration due to gravity. I prefer to work in SI units and will switch back to imperial units in the end:

h=[((2π)² s^-2)(3.05² m²)/(2x9.8 m/s²)=18.7 m=61.4 ft!

What this means is that virtually all the water in the tank would spin out to the walls and spill out. I must admit that this surprised me. To make this a doable problem we must make the surface of the water stay flat; we can do this by putting a flat lid right at the surface of the water. That is what I will now do to answer your question; note that the pressure at the outer surface will depend on the depth.

I will assume that you are interested in the gauge pressure, the pressure in addition to the atmospheric pressure; if you want absolute pressure, add about 14.7 psi. First, assuming the tank is not rotating at all, write the pressure of the water (P_w) a depth d below the surface; P_w=ρgd where ρ=10³ kg/m³ is the density of water. So, at the surface (d=0) the pressure is zero and at d=6 in=0.152 m, P_w=1490 N/m²=0.216 psi. The pressure at any depth d is P(d)=(0.216/6)d=0.036d where d is in inches. That was gravity without rotation; next do rotation with no gravity. (I am going to do this using calculus, so if you don't know it you can just jump to the end.) All infinitesimal volumes of water (dV=rdφdzdr) will have a centrifugal force dF_c=(v²/r)dm where r is the distance from the axis of rotation, v=rω is the speed of the tiny volume, and dm=ρdV=ρrdφdzdr is its mass. You will note that the pressure depends only on r and if you do all the integration you will find that P_c(r)=½rω²ρ. I find that P_c(r)=6.02x10⁴ N/m²=8.73 psi. Finally you can simply add P_c and P_w to get P(d)=(8.73+0.036d) psi.

QUESTION:
I am in the middle writing what I believe will be a series of speculative fiction novels which take place in the far future. I've been working on them for over 20 years while I was working my normal job. Now that I'm disabled, I've become ENABLED to focus 100% of my energies on completing this first book. I'm fairly decent at basic math but I was never taught how to utilize mathematical formulae - I'm forever sorry about it. As such, I was wondering if it's possible to put a basic math series of steps together for me to be able to fill in the slots to figure out how fast a large rotating ring would need to spin to achieve the equivalent of 1G (9.81 m/s2) for an orbiting ring with a radius of 132,500,000 kilometers? I have all the statistics of my habitat ready to go, I just need to know where to put which number and then a.s.m.d. which to which to get to the needed number.

ANSWER:
The acceleration a of an object moving with speed v on a circle of radius R is a=v²/R so v=√(Ra)=√(1.325x10¹¹x9.81)=1.14x10⁶ m/s; the acceleration is a vector directed at the center of the circle. Suppose that object was a person of mass m. The ring would have to exert a force F=ma on her to keep her moving in the circle; she would interpret the force she felt from the ring as a force force pushing her against the ring (centrifugal force), and she would feel like she felt on earth. With a speed of 1.14x10⁶m/s, the rotational velocity would be ω=v/(2πR)=1.3x10^-5 revolutions/second=425 revolutions/year.

Have you ever read Ringworld by Larry Niven? Your world sounds a lot like his.

QUESTION:
I have a piece of metal that is designed to pass an electromagnet at very high speed. The set up is that the electromagnet is designed to manipulate this piece of metal as it passes it. I need to know how quickly an elctormagnet can be turned on and off and on and off again in order to affect the peice of metal - the important fact is it is travelling very quickly indeed. For example, if this were to be posed as a circlar movement of the metal as the hand of a clock and the electromagent sitting at one side outside of the perimeter of the clockface, say at 8 oclock, this metal piece could easily be achieving speeds akin to a high powered motor. Yet at the same time the magnet musty be able to give full effect, turn off and given this thought example turn back on again at the next pass. Can an electromagnet react this quickly?

ANSWER:
I don't know the details of your device, but I can tell you that very rapid changes of magnetic fields from electromagnets are very difficult to achieve. The physics reason is that electromagnets are always coils of wire which have an inductance which, because of Farraday's and Lenz's laws, resists changing the current in the wire. Even a current in a simple circuit cannot be instantaneously turned on or off because of the inductance of the single loop of current-carrying wire. I would encourage you to study up on inductance.

QUESTION:
When we throw light on opposite wall in an elevator by a torch, the light bends . Is is it because the photons leaving the torch move with constant velocity but the opposite wall of the elevator accelerates and we see it as bend?

ANSWER:
The light does not "bend" if the elevator is moving with a constant speed, only if it is accelerating. Also, you must imagine the elevator in the middle of empty space, no gravitational field. This is going to be one of my long-winded answers because it is a good learning opportunity on several levels. I will change your question slightly because it is more conventional to consider this problem if the light source is outside the elevator and enters through a small hole in the side; the light moves perpendicular to the velocity of the elevator as seen by an observer at rest outside.

First let's look at the case where you are in the elevator moves with constant velocity v and and there is also an observer at rest watching you go by. You, in the elevator see the light follow a path shown by the solid red line. The length of this line is d=√(L²+(vt')²) where t' is the time your clock measures from when it entered until it hit the opposite wall. The time it takes t'=d/c where c is the speed of light. It is a straight line because v is constant and, for example, the elevator has moved d/2 at t'/2. Meanwhile, the stationary observer sees the light move straight across (dashed red line) and strike the wall at the same place because the wall has moved up in the time it takes to go across which is t=L/c where t is the time measured using his clock. Therefore, the clocks of the two observers do not run at the same rate. Now, the time the observer measures is t'=√(L²+d²)/c where d=vt' is the distance the elevator has traveled. Now, putting it all together and doing some alegbra, (t'/t)²=(1+β²(t'/t)²) which leads to t'=t/√(1-β²) where β=v/c. This is the famous time dilation formula.

Finally, let's consider the case of the accelerating elevator. I will assume that you, in the elevator, have measured the acceleration to be a and the the velocity at the instant that the light pulse enters the elevator is zero; therefore, v'=at'. The outside observer sees exactly the same as he saw with constant velocity: the light goes straight across and then strikes the wall wherever you saw it strike the wall. You, however, see the light follow a parabolic path (it would seem*) since the position of the elevator is z'=½at'². This was the thought experiment by Einstein where he realized that there is no experiment you can perform in an accelerating system in empty space which would not have the same result in a uniform gravitational field, the equivalance principle, a cornerstone of general relativity.

*The previous part of my answer (accelerating) is technically wrong but conceptually correct. The actual mathematics and physics become quite technical. The main reason it is not easy is that acceleration does not play the important role it does in Newtonian mechanics because it is not the same for observers. Also contributing to the fact that the path is not exactly a parabola is that the speed everywhere on the path is c whereas the speed increases as it falls for an object with mass. Also emphasizing the difficulty here is that, when Einstein first calculated the deflection of light by a star, he made an error of a factor of two.

ADDED THOUGHT:
If you want to learn more about how acceleration and force are treated in relativity, see the links on this subject on the FAQ page.

QUESTION:
I have had this theory for about three years now and I was wondering if you could see if this is valid or not. My question is, if everyone person except the pilot on a passenger plane were to all stand up and jump at the same time, would the plane drop or be disturbed at all? I feel like it would be disturbed as average mass it at 60-70kg each therefore surely it should move.

ANSWER:
This is not a "theory", it is straightforward Newtonian phyics. For an isolated system (which we can consider the plane plus passengers to be, approximately) the linear momentum must be conserved. Suppose that there are 200 passengers each with mass 80 kg in a Boeing 737-100 with mass 28,000 kg. If each jumps so that they go up 40 cm, they need to have a speed of v=√(2gh)≈2.8 m/s. Their momentum is p=80x200x2.8=4.48x10⁴. The plane must recoil downward with the same magnitude of momentum, P=28,000V=4.48x10⁴ so V=1.6 m/s=3.6 mph. The plane is flying with an approximate speed of 600 mph, so this would not be very violent, certainly not nearly as much as bumpiness due to turbulance; and when everyone returned to the floor there would be no vertical speed at all again.

QUESTION:
I understand that the speed at which time passes varies with altitude, or more accurately, with the strength of the surrounding gravitational field. I also understand that the speed at which time passes changes for an observer as their velocity changes (I.e. time dilation effect as you approach the speed of light). So... is the a difference in the speed time passes between a point at sea level at the equator versus at sea level near one of the poles?

ANSWER:
The first part of your question alludes to gravitational time dilation. However, your question asks only for the comparison of clocks where the gravitational field is the same. So my answer will discuss only the normal time dilation. Suppose that you have a clock on the north pole. You observe a clock at the equator which has a speed of about 464 m/s. When if you observe your clock to tick off 1 s, the clock at the equator will click off a time t=1/√(1-(464/3x10⁸)²)≈1+1.2x10^-12 s, a very tiny bit slower than your clock.

QUESTION:
I'm researching issues of physics and wanted just a clarification, specifically with regards to gravity. I've heard it said what actually keeps gravity from crushing us is the electromagnetic force - that the electrons in our bodies are pushing against the other atoms, which keeps us from being crushed. Is this true?

ANSWER:
Well, interactions between atoms are primarily electromagnetic and interactions betweeen atoms can bind them together to make a solid. If there are to be living beings, that binding must be strong enough so that it is not broken when the gravity tries to push each atom in a solid down; any evolution will certainly be driven by the environment and gravity is a very important part of the environment. An instructive example might be an ice cube. It sits on the table top not being crushed. But as it melts the bonds break and the water spreads out on the table as gravity "crushes" it. If you did not have bones you would probably end up pretty flattened on the ground.

QUESTION:
Can gravity be used to create energy, and if so, can dark matter be used to create energy?

ANSWER:
Drop a ball and it gains energy; gravity is giving it that energy. Water from a reservoir runs down and spins a turbine to generate electricity; gravity is causing that energy to be generated. You have to be careful with the word "create" though. The total amount of the energy in the universe always remains the same and our manipulations simply convert one kind of energy to another. I wouldn't speculate about dark matter, though, because nobody actually knows what it is in any detail at all.

QUESTION:
I keep reading/hearing on videos that there have been experiments to prove that the speed of light is the same for all observers. A sample claim is "Since Maxwell's work, numerous experiments have been performed to test the prediction that electromagnetic radiation travels at the same speed for all observers - and none have failed." The articles or videos never go into any additional details on the experiments.

ANSWER:
Let's first talk about the origins of the idea that light in a vacuum has the same speed regardless of the motion of the source or the observer. Maxwell's equations, the equations of electricity and magnetism, unambiguously predict this behavior. When Einstein developed his theory of special relativity, perhaps the most important postulate was the constancy of the speed of light, c. The predictions made by special relativity were revolutionary and would be false if c were not a constant for all observers. So, certainly the most important and accurate experiments verifying constant c were experiments checking the predictions of special relativity. No experiment was ever performed which contradicted the predicitions. If you are not familiar with special relativity, look up time dilation and length contraction. Incidentally, no prediction of Einstein's theory of general relativity (our best theory of gravity) has ever been found to not agree with experiments.

QUESTION:
I only went through Physics 2 in college so I am a relative rookie, albeit a long in the tooth rookie. My Question is related to Quantum Mechanics. If a particle, electron or whatever is spinning one way; and we send it through a magnetic field of one direction or the other; and the object goes up or down or right or left and supposedly we know it's spin. I understand that sometimes, however, we send it through again and the spin is different. The question may be stupid but for a rookie we think of simple things like English on a pool ball, it can put the opposite spin on an object it collides with. So the question is do physicists consider friction and it's effect on spinning objects when measuring these things?

ANSWER:
This is a really hard question to answer. Electrons do indeed behave like they have an angular momentum. We generally refer to this angular momentum as intrinsic spin or just spin. We are therefore led to believe that they are actually tiny spinning balls, just like the English on a billiard ball. But, as is almost always the case, we generally run into trouble if we try to apply our classical physics to quantum physics. For example, consider a proton whose spin quantum number is, like the electron, ½; its actual angular momentum S is S=ℏ√[½ (1+½)]=0.87ℏ where ℏ is the rationalized Planck constant. Suppose now you put in reasonable numbers for the mass and radius of a proton, assume that it is a uniform sphere, and calculate the rate of rotation. You find a totally nonphysical answer; the surface of the sphere would have to move faster than the speed of light! Certainly when particles collide with others their spins will be affected depending on how they interact; to find out the details you would have to do quantum mechanical calculations. Friction is a wholly macroscopic concept and has no existence in a microscopic world. Also, the way we observe spin is to observe the requisite magnetic moment of the particle; recall that a current loop has a field just like a tiny bar magnet and a charged particle with spin will be a tiny current loop. A bar magnet in a uniform magnetic field will experience a torque but no net force; you must make the field non uniform for the particle to see a force. It seems that you are a little hazy on how this observation is done and you should study the Stern-Gehrlach experiment to sharpen up that understanding.

QUESTION:
Plane 1 and Plane 2 have same mass and surface area. If plane 1 starts its flight by applying 500N force (numbers are rough and just for illustration), Then it would accelerate. But when speed increases - air resistance increases, if the plane applies the same 500N force throughout its Flight then soon acceleration decreases and the plane will reach terminal velocity due to the opposing force of air resistance. ( I have applied Newtons second Law ) If plane 2 starts its Flight with 1000N force, then it would accelerate more than Plane 1. As the speed of plane 2 increases faster than plane 1 - so will its air resistance. If the flight applies the same 1000N force throughout its flight - eventually its acceleration decreases and the plane will reach terminal velocity due to the opposing force of air resistance. ( I have applied Newtons second Law ) So how come two flights with different force reach their destination at the same time according to Newton's second Law???

ANSWER:
They do not reach the destination at the same time because the terminal velocities of each are not the same. Terminal velocity v is achieved when F=Cv² where F is the applied force and Cv² is the air drag; so v=√(F/C). But you told me that C is the same for both planes (same mass, area), so v₂/v₁=√(1000/500)=1.4.

QUESTION:
Is refraction an actual physical phenomenon, or is it a strictly biological perception, like with touch? To elaborate, does light actually bend from its path when its refractive medium is changed, or do we only see it a such?

ANSWER:
What a strange question! Of course it is an actual thing. If refraction didn't really result in bending the path of light, your eye would not work; your eye captures light from some object and bends that light (using a lens) to form an image on your retina which is then interpreted by the brain. Likewise with cameras and telescopes. I have attached a photograph of light rays being bent to a focus by a convex lens; the camera which took this photo would not be able to see a "perception". Maybe you are thinking of whether a stick stuck into water is really bent like it appears to be; no, but it looks like it is because the refraction is bending light rays.

QUESTION:
Newtons cradle: When you release 2 balls and they send their kinetic energy down the line,2 balls on opposite side move. But why doesn't it just send one ball much higher?

ANSWER:
Newton's cradle is usually explained assuming all collisions are perfectly elastic. Therefore, both kinetic energy and linear momentum must be conserved. Suppose that two balls, each of mass m, move together with speed v₁ when they hit the other balls. Then the initial linear momentum is p₁=2mv₁ and the initial kinetic energy is K₁=½(2m)v₁²=mv₁². Now, suppose a single ball exits the other side with speed v₂; its linear momentum must be equal to p₁=2mv₁=p₂=mv₂, so v₂=2v₁. Now, what is the final kinetic enregy? K₂=½mv₂²=2mv₁², twice the initial energy. Therefore energy is not conserved so this cannot happen.

QUESTION:
If a singularity is a small point inside of a black hole where there's infinite density, does that mean if we take an iota of that singularity (presuming its tangible or transportable in its ways) would that be able to sustain gravity within a spacecraft or would that iota of singularity overpower everything in its way

ANSWER:
You are asking if you could use some small black hole to provide a gravitational field in a spaceship. Suppose that we put the black hole a distance R=1000 m from the captain's chair. What mass M would be required to make the gravitational acceleration the same as on the surface of earth (9.8 m/s²)? So, a=F/m=GM/r²=6.67x10^-11M/10⁶=9.8 or M=1.5x10¹⁷ kg. But the field would decrease rapidly away from the captains chair and increase rapidly toward the black hole; e.g., 10 m away from the captains chair there would be an acceleration 9.8(100/110)²=8.1 m/s² and 10 m closer to the black hole 9.8(100/90)²=12.1 m/s². Also, how would you hold it there? Anything close to the black hole would would experience huge gravitational forces tending to obliterate whatever was holding it.

QUESTION:
For example I'm going to home with my car at 40mph and I open my car's lights. These photons from my car won't go over the speed of light and my 40mph wont gonna add to this speed so what happend to this speed to this energy. Where is it go?

ANSWER:
You are right, the photons emitted forward from a source moving forward have more energy than if the source were at rest. You are also right that either photons will be going the same speed. So, how could their energies differ? The energy of a photon is E=hf=hc/λ where h is Planck's constant, c is the speed of light, f is the frequency and λ is the wavelength. So the wavelength of the gets shorter if the energy gets larger. This is just the Doppler effect for light and in this case it is referred to as a blue shift. No energy has been lost. (By the way, since 40 mph is so small compared to c, it would be really difficult to observe any effect at this speed.)

QUESTION:
I have a question that is driving me crazy. I'm a children's author; my stories have appeared in Highlights magazine. I'm working on a middle-grade novel in which the protagonist plays lacrosse. The boy's father is an engineer who is fond of explaining how things work, and at one point he and his son have a discussion about what keeps a lacrosse ball in its pocket when a player is cradling (i.e. the rocking motion a player makes with a lacrosse stick to prevent the ball from falling out of the pocket). I've researched this endlessly online and most explanations claim centrifugal force is what keeps the ball in the pocket. But a few claim that it's actually centripetal force. I tend to think that is the correct answer: the ball wants to fly off in the same path as the head of the lacrosse stick as the player swings it back and forth, but the pocket's mesh netting gets in the way and keeps the ball in the pocket. It would be the same force that stops water in a bucket from following the path of inertia and spilling out and when you swing it over your head in a big circle. BUT ... I'm simply not sure.

ANSWER:
It all depends on who is observing the ball. Let us, to keep the situation simple but still illustrate the basic principles, assume that the ball is moving in a horizontal circle of radius R with a speed v. We focus our attention on the ball as we observe it watching the game. (I have drawn three Cartesian coordinates shown in green to help visualize.) First, find all the forces on the ball. (Ignore the dashed vector labeled C for now.) Two things exert forces on the ball, the earth (gravity) and the netting. The earth force is called the weight as W in the diagram; the netting force I have broken into its vertical (F_V) and horizontal (F_H) components. The vertical component is equal in magnitude and opposite in direction to W to ensure that the ball moves horizontally rather than fall vertically as the weight would have it do; the horizontal component (centripetal force) keeps the ball moving in a circle and provides the acceleration of a=v²/R which points toward the center of the circular path. You can now calculate the force F_H from Newton's second law, F_H=mv²/R where m is the mass of the ball. So, there is your answer: the ball continues to be in contact with the net because the force the net exerts on the ball causes the ball to accelerate; as long as the player keeps changing the direction and/or speed of the ball, it can be kept in the net. This is the centripetal argument.

But, what about the centrifugal force which seems to be the majority opinion? Is it wrong? Not if you understand what a centrifugal force is. Imagine that you are the ball and you wish to use your coordinate system to understand the physics. In your coordinate system you are at rest so all the forces on you, according to Newton's laws, must add up to zero. What are all those forces? Exactly the same as when you observed the ball from the stands. There is nothing else but the earth and the net which can exert forces on you. What this means is that Newton's laws are false if the observer is accelerating relative to some coordinate system in which they are true. So what do we do? We invent and add in a force which compels the system to obey Newton's laws. That force is called a fictitious force and in this case it is the so-called centrifugal force. So we add the vector C=-F_H to make the sum of all vectors equal to zero even though it does not exist! So this is the centrifugal argument since clearly C is holding the ball to the net in this picture. Is it "cheating" to just add a nonexistent force? Not if you do it for a good reason. Newton's laws are great and greatly help understanding what is happening. As long as you know what you are doing, if you can force Newton's laws to work, you can often more easily solve the problem.

Finally, just a little linguistics! Fugo is Latin for I flee (the root of fugitive); centrifugal is center-fleeing. Peto is Latin for I seek; centripetal is center-seeking.

QUESTION:
I am 17 years old and I want to know why like charges repel and unlike charges attract. I know this is due to the exchange of virtual photons but I am interested to know the deep facts in simplified way. I have read this, but it is still complicated to me. I would be grateful if you simplified it.

ANSWER:
Gravity has only one kind of force, attractive, because there is only one kind of mass. However, electrostatics has two kinds of force, attractive and repulsive, so there must be two different kinds of electric charge. Measurements are able to determine the forces quantitatively (Coulomb's law). One can build up everything we knew before the early 20th century about classical electromagnetism by taking the attractive/repulsive nature of electric charge as axiomatic and based on measurements; physics, after all, is an experimental science at its heart. But just like Einstein sought an answer to "why" masses attracted each other, physicists (e.g. Feynman, Dyson, Schwinger, Tomonaga, et al.) developed quantum electrodynamics (QED) which quantized the electromagnetic field and therefore provided a theory for the interaction between electric charges. Unless you are an extraordinary genius, at age 17 you will not have the mathematical toolbox needed to understand the theory beyond the qualitative understanding you have (exchange of virtual photons); if you are that extraordinary genius, you should not need me to explain it to you!

QUESTION:
It's a simple question, but I can't find an explanation. What is the total energy of a block which is at rest, at ground level on a flat, frictionless surface? Intuitively it should be zero, since it is not moving (no KE) and it's "height" above the ground is effectively zero (so V=mgh=0) However, I thought an object with mass must have energy.

ANSWER:
More specifically, we would say that (provided that we have chosen the ground to be zero potential energy) the total mechanical energy of the block is zero. Still, it has rest mass energy mc².

QUESTION:
I have a question for you. In your book "Atoms and Photons and Quanta, Oh My!" appendix B page B-2 Energy in special relativity, you derive E=mc^2 using an approach I've not seen before. What I don't get is the 2nd line where F = m (d[v/(1-v^2/c^2)]/dt), where m is the rest mass. Can you show the steps you took that aren't showing (to save space)? I don't see how you arranged this expression to include the differential operator "d". I've seen/used several derivations using differentials & integration by parts & so forth from old physics texts & on-line.

ANSWER:
Here is a screen shot of the page the questioner is referring to:

So, keep in mind here that m is rest mass, F is force, p is linear momentum, K is kinetic energy, W is work, v is velocity, c is speed of light. In classical mechanics, p=mv. But, if v is not very small compared to c, p must be redefined or else it will not be a quantity which is conserved if F=0. The correct definition in relativity is p=mv/√(1-(v²/c²)). So the second line (after F=dp/dt ) simply inserts the expression for p. The third line multiplies and divides by dx and rearranges so as to have v=dx/dt appear as a factor. The fourth line rearranges and replaces dx/dt by v. Finally, the fifth line is the result of evaluating the derivative with respect to x:

m(d/dx)[v(1-(v²/c²))^-1/2]

=m(dv/dx)(1-(v²/c²)^-1/2+(-½)(v)(1-(v²/c²))^-3/2(-2v/c²)(dv/dx)

=m(dv/dx)(1-(v²/c²)^-1/2[1+(v²/c²)/(1-(v²/c²)]

=m(dv/dx)(1-(v²/c²))^-1/2[(1-(v²/c²))^-1]

=m(dv/dx)(1-(v²/c²))^-3/2

To do this last step you need to know your elementary differential calculus, (d/dz)(f(z)g(z))=f(dg/dz)+g(df/dz) [product rule] and (d/dz)f(g(y)=(dg/dy)(dy/dz) [chain rule]; and, of course, a bit of algebra.

QUESTION:
If a raindrop is affected by the earth's gravity and it should accelerate at a rate of g(9.8m/s^2) downward. Why does when it hits the ground it doesn't result in a big impact?

ANSWER:
Yes, a raindrop experiences the downward force of its weight; but it also experiences an upward force due to air drag. The drag force depends on the drops size and speed and increases like the square of the speed. Eventually the speed reaches a point where the upward force of the drag is equal the the downward force of the weight and the drop stops accelerating. This speed, called the terminal velocity, is usually about 15-25 mph depending on the size of the drop.

QUESTION:
Can gravity efect electron velocity?

ANSWER:
Yes, see a very recent answer. But you would have trouble seeing it. An electron which is accelerated over 1 volt has a speed of about 6x10⁵ m/s=1.3 million mph!

QUESTION:
So I know that gravity is caused by mass curving spacetime and all mass following those curves. That would explain how something is pulling something without actually touching it. But a question arises. If gravity is a curve in spacetime, how do magnets attract each other? Yes, I know that magnets create magnetic fields but what are those fields exactly? They just feel like some magic arrows that go in and out of magnets. I haven't really seen anyone explain this so if you can help me understand this I'd be grateful.

ANSWER:
There are four fundamental forces in physics, gravity, electromagnetism, the strong nuclear force, and the weak nuclear force. To answer your question, I only need to discuss gravity and electromagnetism. Electric forces and magnetic forces are two faces of one force, the electromagnetic force. There are two kinds of electric charges which are characterized by assigning a sign, plus or minus. Two electric charges will repel (attract) each other if they are of the same (opposite) sign; they do so because of the electric fields they produce. But an electric charge can also cause another type of field if they are moving, called a magnetic field, which we can associate with electric currents. The simplest electric current is simply a tiny current loop as shown in the figure. Notice that the magnetic field points toward the loop at the bottom and away from the loop at the top; the field of this loop looks just like the field of a tiny bar magnet as suggested by labeling below the loop S (south) and above N (north). Many atoms look like a current loop and hence like a tiny bar magnet. In most materials all these atomic loops are randomly oriented such that they cancel each other out. In a few very special materials the fields of the atoms tend to line up with the fields of their neighbors and the whole object is said to be magnetized. The electromagnetic field has also been quantized which means that we understand microscopically the details of how the forces are communicated among currents and charges; the field quanta are called photons (tiny parcels of light, really) and these are the "messengers".

Gravity may be interpreted, as you note, as geometry, a warping of spacetime. However, general relativity (Einstein's theory of gravity) is also a field theory; nobody has yet been able to quantize the field. When (if?) gravity is successfully quantized, the field quanta would be called gravitons.

One additional detail: electromagnetic and weak nuclear forces have been unified, shown to be different faces of a single force, the electroweak interaction.

QUESTION:
Can gravity slow down the atom ?

ANSWER:
You are asking, essentially, if atoms feel gravitational forces. Anything which has mass will feel the gravitational force and atoms have mass; so, yes, atoms experience the gravitational force and thus can be made to slow down. For example, if you shoot an atom straight upwards, it will slow down just like a baseball thrown upward with the same speed. The very fact that we have an atmosphere is proof that gravity is acting, keeping all those atoms from speeding off into space.

QUESTION:
What is the smallest change in frequency within the visible light spectrum that the human eye/brain can discern? My new TV says it can show over a billion colors. Can humans even see 1 billion colors!

ANSWER:
The way a tv works is by mixing the three primary colors, red, green, and blue, in varying amounts. There are an infinite number of possible ratios. All the colors you can see are not all the possible wavelengths you can see (also an infinite number) but mixtures of many many wavelengths. When the manufacture refers to "billions" he is probably referring to how accurately the electronics can mix the three. For example, if the relative amounts of the three were 10, 7, 3, the electronics would have an uncertainity in how accurately they could set these numbers; maybe the numbers could only be set to a 0.01% accuracy, the ten would be 10±0.0001. Then you could estimate the number of possibilities you could have over the whole visible spectrum.

QUESTION:
I have been thinking about this for countless hours and though not a physics student, and haven’t taken any classes of the sort I have wanted to know this question: we know black holes are brought down to a point of singularity. So could and atom being so small do the same? And if this is true would that be the last atom we see on the periodic table?

ANSWER:
The force which holds a star together is gravity; a normal star does not contract to a black hole because it has collapsed to the point where burning hydrogen (fusion) in the star heats it up so that the pressure balances the gravity trying to push it smaller. As the fuel runs out, the star starts getting smaller. At this stage, various things can happen, depending on various conditions, mainly the total mass of the star; one possible thing is eventually collapsing all the way to a black hole. An atom is a completely different kettle of fish. We should really look at the nucleus since that is where nearly all the mass is. Unlike a star, energy is not being produced in the nucleus, its energy remains constant. An atomic nucleus is held together not by gravity but by the strong nuclear force. Unlike gravity which is a very long-range force, the strong interaction is very short range, so each proton and neutron see only their near neighbors, not all the other particles in the nucleus. The result is that the heavier a nucleus becomes, on average, the less bound it comes so its tendency is to break apart, not collapse. By the way, the nucleus does not collapse because the nuclear force at extremely short distances becomes repulsive, not attractive.

QUESTION:
How much does a thought weigh? And how much does one molecule of carbon dioxide weigh? I want to compare the two.

ANSWER:
A molecule of CO₂ has a mass of about 7.3x10^-26 kg (about 1.6x10^-25 lb). A "thought" is a collection of billions of electrical impulses and chemical reations in the brain. Even if these could be assigned a "weight", which they can't, all "thoughts" are not the same and would have different weights.

QUESTION:
Franklin first coined the term negative and positive in 1750 and Volta invented the battery in 1800. Did Volta assign a positive and negative end to the battery? Or did he think the negative and positive applied to electrostatics and not "flowing" electricity. You see where I am going with this. I need to go up the chain to J.J. Thompson to see where the goof up was on adoped circuit diagrams. The explanations I have read are non sense. They do not actually describe why the convention had to be reversed. All the examples I read use circular reasoning and thus far no smoking gun of how and when the goof up happened. I thought if I could start with Volta I might be able to unravel it.

ANSWER:
I really don't understand your perception of "goof up". There are two different "kinds"of electric charge. 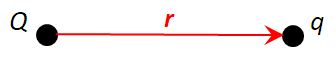Coulomb's law shows that the magnitude of the force F which a point charge q feels due to the presence of another point charge Q is proportional to the product of the charges Qq and inversely to the distance r between them, F∝Qq/r². Also, if the charges are of the same "kind" they repel and of different "kind" they attract; since attract/repel result in exactly different directions for the vector force if we randomly assign signs to the two "kinds", we can write F∝1_rQq/r² where 1_r is a unit vector in the direction of the vector r from Q to q, 1_r=r/r. This proportionality does not depend on which "kind" we call positive and which we call negative, there is no right and wrong choice for the sign for an electron. Franklin made a random choice which resulted in electrons as having negative charge; he might have made a different choice if he knew electrons existed and were usually the charge carriers in currents (nobody knew then), but it was not a wrong choice. Later, when currents and magnetic fields were studied, all of electromagnetism simply continued the original choice with no problem whatever. All this means that positive electric currents in wires actually are almost electrons moving in the opposite direction which is endlessy confusing to students. I really don't know anything about Thompson correcting "a goof up" in circuit diagrams other than pointing out that currents shown moving in one direction (from + to - battery terminals) is actually electrons moving in the opposite directions. No physics was changed.

QUESTION:
What will be the motion of the earth if the sun disappears after t=0 sec?. I was asked this question in an exam and the answer is not tangential to the motion

ANSWER:
It is assumed, although never very accurately measured, that the speed of gravity is the same as the speed of light. Therefore, the earth would continue in its orbit until t=8.3 minutes, the time it takes light from the sun to reach the earth. At that time the earth would go dark and proceed in an approximately straight trajectory.

QUESTION:
How do gravitons that exit a certain mass cause other objects to be attracted to that mass. I can imagine Einstein's idea of curved space being the cause for the seeming attraction, but what does that have to do with gravitons?

ANSWER:
There is no successful theory of quantum gravity; therefore gravitons are hypothetical particles, never observed, just an idea. Gravity is the only one of the four fundamental forces of nature which has not been quantized. See an earlier answer and the links in that answer. You will see that the theory of general relativity is not unambigously described by the notion of warped space-time but is also a field theory. Any field theory should be able to be quantized; in a quantized field theory the "messenger" of the field would be called a graviton, just as the messenger for the electromagnetic field is the photon, and is the gluon for the strong nuclear field.

QUESTION:
Why does a rounded pencil I put on a flat ground make a small harmonic movement before stay steady?

ANSWER:
One side of the pencil is heavier than the other. For example, if you had a uniform ball and glued a weight to its surface, it would always rotate so that weight would go to the ground. With some pencils the lead in the middle is not exactly on the axis. The "lead" is actually graphite (carbon) with a density of 2.26 g/cm³; wood has a density of about 0.6 g/cm³. So the lead will seek its lowest p

ossible point it can possibly find. The figure illustrates this situation. The weight of the lead will cause the pencil to roll to the right; but when it gets there it will be moving and so the pencil will continuing to roll until the lead stops and then begins rolling to the right. It will oscillate forever if there is no friction; but there is so it will quickly damp out with the lead directly below the center axis of the pencil.

QUESTION:
I am a glass artist. When I fume gold (vaporize in the torch flame) and it collects onto the borosilicate glass it appears pink/purple. If I encase this gold with clear, it then looks green. I can throughly manipulate the glass and maintain the green color. I read that Faraday obtained green gold in a thin film with stress on the film. I also fumed gold onto a rod and stretched it at a fairly cold glass working temperature to stress the gold and avoid annealing the gold. The gold took on a green appearance. I have been doing this for over 25 years and have not been able to find out why gold turns green when encased (or stressed like with the stretch) I am asking a physicist because this has to do with light and gold, plasmon resonance etc are pretty heavy topics. If you can answer this question I’d love to gift you one of my art works! Why does a thin film of gold turn green when encased in glass?

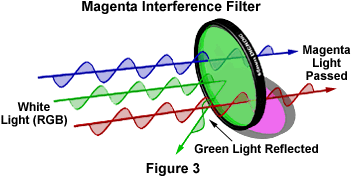
ANSWER:
I am not sure why it is pink/purple when you first deposit it. One video suggested that has to do with the amount of oxygen in the film; it is also possible that it is a thin-film interference effect where the thickness of the film is an integral multiple of wavelengths of the color you are seeing and the light of that wavelength which is reflected from the front and back of the film add up to become the dominant light you see (the same thing going on in the pretty colors you see on an oil slick). There such things which use thin-film interference, for example the magenta interference filter shown in the figure.

Now, to the green issue. Why is gold the color we see with just a block of gold? The reason is that when white light strikes the surface, red/yellow/orange are preferentially reflected back making the gold look golden. But some of the light will continue into the bulk of the gold, and, coincidentally, red/yellow/orange are preferentially absorbed. This means that once you get to a certain depth in the block the only light surviving is the blue/green part of the spectrum; eventually all the light gets absorbed and you will see no light coming from the back side which originated on the other side. However, if you have a "block" which is thin enough, smaller than the distance where everything is absorbed but thick enough that all the red/yellow/orange has been absorbed, the film will look blue/green. I am quite sure that this is what is going on but, since I don't know the geometry of your art, I do not have a detailed explanation for your particular situation; e.g., does it look green when seen from any direction? Maybe if you sent a photo or two I could go farther.

I have a question for you. I am a stained-glass hobbiest and find that red glass is often more expensive than other colors. I have been told that the reason is that gold is required to get a rich, pure red glass. Do you know if that is true and/or why?

QUESTION:
A thought occurred to me. From what I know about particle accelerators, scientists speed up accelerator particles of matter and crash them into slower moving or stationary particles of matter so that they can examine the breaking apart of all into other elementary particles. This then allows them to find more and more basic particles of matter. I have read that the speeds these accelerator particles are hoped to reach is the speed of light, hence the effort to build more powerful particle accelerators. So, why not simply have photons of light (that are travelling at the speed of light since they are the elementary particles of light) crash into those other particles of matter? Why use so much energy trying to push accelerator particles to reach the speed of light, when we have light in the first place and photons already moving at 186,000 miles per second?

ANSWER:
It is not the speed of the incident particles which matters, it is their energy. There are no good available sources of high-energy, high-intensity photons. Also, photons interact only via the electromagnetic force and we often want projectiles which interact via the strong nuclear interaction. So the accelerators are actually poorly named because they do almost no change in velocity when they increase their energy by a large amount; I have maintained that they would better named energizers. For example, a proton with speed 99.999% the speed of light accelerated to 99.9999% the speed of light increases its speed by 0.0009% but its energy increases by 216%.

QUESTION:
A photon hits an atom perpendicularly to its speed v and it is absorbed as is known immediately. So it can not act after the time when it is not perpendicular (e.g. the force is 0 after that). Certainly all its energy goes to the atom when it is perpendicular to v.

But the impact (absorption) applies a force on the atom and it is postulated that a perpendicular force can not do work. So work has not been done on the atom. Consequently its energy can not change. If all photon energy goes to increase internal energy of an orbit electron from Eo to E1 how then is the DIRECTION of velocity of the atom changed? Isn’t this a contradiction?

ANSWER:
Your first paragraph really makes no sense. Talking about "perpendicular" in a collision really has no meaning; I think what you mean is a head-on collision, one where the recoil of the atom is in the same direction as the incident photon. In a case like this you do not want to think about force and work. Rather you should ask if energy and momentum are conserved; if so, you should solve your problem that way. Suppose that the system we are interested in is the photon (mass zero, energy E=hf, and momentum p=hf/c) plus the atom (rest mass M, energy E=Mc², and at rest p=0). Because there are no external forces on this system, its total energy and momentum must remain constant. After the absorption, the mass of the excited atom is M', its kinetic energy is K, and its momentum is P'; there is no need to think about what goes on microscopcally inside the atom. So we have two equations:

E₁=E₂ or hf+Mc²=M'c²+K

p₁=p₂ or hf/c=P'.

The notions of force and work are seldom useful when looking at atomic sizes. In this case, the photon carries energy into the atom so the atom's energy has to increase.

QUESTION:
If l video an energy source such as a man-made Ultraviolet Curing light, can watching the video hurt your eyes? And is there a way of capturing this light to make it even though it is invisible?

ANSWER:
The video camera is not sensitive to UV light and therefore records none. The monitor is designed to emit almost entirely visible, not UV light and therefore radiates none. So no, the video will not hurt your eyes. There are certainly detectors which do detect UV radiation but it is not really 'capturing' it in the sense that you could 'make' it.

QUESTION:
This question has resulted from considerable back-and-forth communications between me and the questioner. The essence of the question is this: Two cylinders are rigidly attached to each other. The smaller has a radius R and its center axis (B in the figures below) is separated by a distance d from the center axis (A) of the larger. A torque is applied about the axis of the smaller cylinder but exerts no net force. Find the resulting torque about the axis of the larger cylinder.

ANSWER:
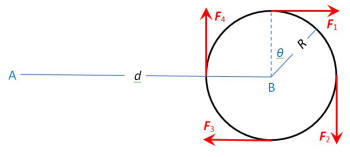The figure shows one possible way of exerting a torque about point B. The four tangential forces all have magnitude F/4 so that the torque is τ_B=RF. There is a net force of zero. The torques about the point A are:

τ₁=RF/4

τ₂=(d+R)F/4

τ₃=RF/4

τ₄=-(d-R)F/4

When all four torques are added, τ_A=RF=τ_B.

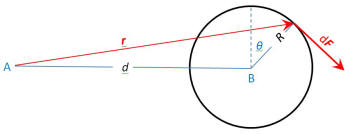A more general approach to the problem would be to have a uniform tangential force all around the perimeter of the smaller cylinder as shown in the second figure. If we write the magnitude of the vector dF as dF=[F/(2π)]dθ, the integral ∫dF from 0 to 2π will be F and τ_B=RF. Now the torque due to dF about A will be dτ_A=|r×dF|dθ=[RF/(2π)][(dsinθ/R)+1]dθ. Integrating this from 0 to 2π yields, again, τ_A=RF because ∫sinθdθ=0 over one whole cycle.

There are two important provisos here: there must be no other forces present which exert torques about axis A and the forces exerting the torque about axis B must sum to zero net force.

Sometimes I like to interject examples of how science is done and sometimes progress hits snags. Most often preconceptions are the biggest stumbling blocks. When I first started to work on this problem I assumed that the answer had to depend on d. As you can see, this is not a particularly difficult problem. I quickly tried the general approach and got the answer as I did above; but I was so sure that d should be in there somewhere that I assumed that I had done something wrong. So I did the calculation for each quadrant individually; these are tedious calculations, not difficult but certainly prone to algebra and arithmetic errors. I spent hours! Finally, when I was sure that everything was right I found τ_A=RF. That was when I tried the simplified torque with four forces (above) to convince myself that it was correct.

QUESTION:
I am trying to clarify in my head an idea regarding electromagnetic force. It is usually explained in very superficial terms. One way to explain my question is this: I understand that two positively charged particles will repel each other, for example two protons. They both have a positive charge, but if they are at rest there will be no magnetic field. Do electrical charges repel like magnetic charges? Are they the same thing? We measure magnetic strength in one set of units such as Teslas but electrical potential in another set of units. I understand the strength of a permanent magnet to be somehow related to the arrangement of its electrical charges. Is that correct? Is a proton at rest a permanent magnet? Is there some simple relationship between a static electrical charge and a permanent magnet? I'm sorry the question is so long but it is all part of one big question.

ANSWER:
Your question violates site ground rules for "single, concise, well-focused questions" in spite of your saying it is "one big question"; even so, it is neither concise nor well-focused. I am sorry, but I cannot give you an entire disquisition on electromagnetic theory in a single concise answer. You have a number of misconceptions. First, there is no such thing as a magnetic charge. I always like to like to refer to an answer to a question I answered long ago:

Answer: The laws of electromagnetism are perfectly symmetric: a changing magnetic field causes an electric field and a changing electric field causes a magnetic field. The first of these is called Faraday's law and the second is part of Ampere's law. You seem to think that only a permanent magnet is magnetism. In fact, any moving electric charge causes a magnetic field. The most common source of magnetic fields is simply an electric current. Here are some facts about electric and magnetic fields:
•electric charges cause electric fields,
•electric currents (moving charges) cause magnetic fields,
•changing magnetic fields cause electric fields, and
•changing electric fields cause magnetic fields.

Magnetic fields are not caused by a charge like electric fields are, they are caused either by electric currents (moving charges) or changing electric fields. So then, what is a permanent magnet? On the atomic level, think of electron orbits as little currents and electrons as tiny spinning charges, also currents. In a material where all these tiny magnets align with each other results in a sum of all their magnetic fields. Regarding your writing "but if they are at rest there will be no magnetic field", this has nothing to do with any force they exert on each other by virtual of their charges. Indeed protons do have a tiny magnetic moment because they can be roughly be thought of as spinning, but those moments are very weak. If you want to really understand all this, you need to seriously study electromagnetism.

QUESTION:
As solar energy is becoming a major, maybe eventually the main source of electricity, I wonder what the effects of capturing and retaining significantly more of the Sun's energy in the system of our planet could be. Would the overall effect be comparable to the warming effect of greenhouse gases, where less energy is radiated back to Space? What about other forms of renewable energy, that ultimately just harness the Sun's energy?

ANSWER:
In greenhouse warming, radiation is absorbed by the earth and then radiated back into the atmosphere; some of that energy goes back into space and some bounces around in the atmosphere, heating it. Factors, including the amount of CO₂ in the atmosphere, determine the fraction of reradiated energy which is trapped. Now, if we capture this energy and store it in batteries, it stores the energy in a form which is not heat; then this energy is used to drive cars, run our utilities, lift material to build buildings, etc., all of which will convert a fraction of the energy to heat, but a much smaller amount than if all that energy were absorbed by the ground and then was reradiated into the atmosphere. And, using this energy instead of fossil-fuel burning will further help the situation by not adding to the CO₂ in the atmosphere.

QUESTION:
I am trying to calculate the energy consumed by an electric bike when it is charging at home. It has a 48V, 14Ah battery and takes about 6 hours to charge. Is the electricity in my power bill going to be 672 watt hours (48 x 14) or ~4,000 watt hours (48 x 14 x ~6)?

ANSWER:
I got exactly the same answer as you but took a different path to get there. Since an ampere is a Coulomb/second (C/s), 1 A·h=3600 C, so 14 A·h=5.04x10⁴ C. The energy to move that charge across a potential difference of 48 V is E=QV=48x5.04x10⁴=2.4192x10⁶ J=2.4192x10⁶ W·s(1h/3600 s)=672 W·h.

QUESTION:
I learnt about the Rutherford experiment where they disproved the plum pudding model for atoms where they used a gold leaf which was apparently 100 atoms thick. I have since read about a gold leaf that was 2 atoms thick. If atoms are mostly empty space why wouldn't you be able to see right through said gold leaf.

ANSWER:
Gold looks golden because it reflects yellow, orange, and red if illuminated with white light. Interestingly, if an object reflects a particular color, it is also a very good absorber of that same color. What that means is that, for gold, yellow, orange, and red will be exceedingly unlikely to get through gold leaf; if any light at all gets through it will be other colors. Indeed, light transmitted through a gold foil will be bluish in color. Typical gold leaf is more than ten atoms thick and two atoms is a very recent achievement, I believe. I would think that the thinner the foil, the more of the gold colors would also transmit through.

QUESTION:
The Laws of physics say nothing can travel faster than the speed of light. Given the universe is expanding, two stars on opposite sides of the universe would be travelling away from each other at much faster than the speed of light. From the perspective of planet a, planet b is travelling faster than the speed of light; how is that possible.

ANSWER:
I presume that you are using Galilean relativity to deduce the speeds of two objects relative to each other if you know their speeds relative to something which you will call "at rest". Let's do an example: suppose that, relative to earth planet a is moving away from you with a velocity V_ay=0.8c and, on the other side of the universe, planet b is moving away from you with a velocity V_by=-0.8c where c is the speed of light. You conclude that the velocity of a relative to b is V_ab=1.6c because the velocity addition formula for Galilean relativity is V_ab=V_ay+V_yb and V_yb=-V_by (or, you might say, just by "common sense"). However, for objects moving with speeds comparable to the speed of light, Galilean relativity, and indeed, all of Newtonian mechanics, are not valid laws of physics. The correct velocity addition formula is V_ab=(V_ay+V_yb )/[1+|V_ayV_yb|/c²]=1.6c/1.64=0.976c.

QUESTION:
I am emailing you with a specific question my 5 year daughter asked my husband and I about rainbows. I’m hoping you might be able to help us, or point us in a direction that would help us with an explanation. We found you online, and we need a professional. We showed our daughter a prism refracting the light just like a raindrop would. She asked, if we hung 100 prisms from the ceiling that should make 100 little rainbows, right? I said correct. BUT!!!! she asked "If each raindrop can refract the sunlight into the colors of a rainbow. Then why aren't a million rainbows in the sky? Why do we only see one big rainbow? How do the reds stay together, the orange together etc...Please help. I haven't been able to find any information on the web.

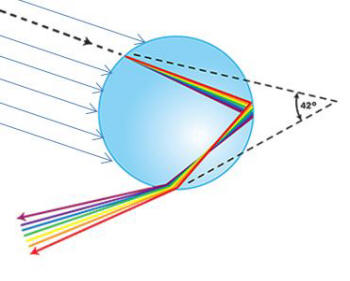
ANSWER:
The prism demonstrates dispersion, the fact that different colors of light travel with different speeds in any medium. The prism is made of glass and the rain drop is water; both demonstrate dispersion but the details are different because the rain drop is a sphere. All the light rays from the sun come in essentially parallel. In my figure, several rays are shown and one is followed as it refracts when it enters the water, disperses into the colors, and strikes the back of the drop; when it reaches the back, part of it goes back into the air (not drawn here), and part of it is reflected back through the water as shown; then it reaches the surface again and part of it refracts back into the air as shown, part of it reflects into the water again (not shown). For this particular ray, and all others from millions and millions of other raindrops for which light enters at the same place on the surface, the emerging light constitutes the rainbow you see. But, note that the angle between the direction of this incoming ray and the exiting "rainbow rays" is 42°. But, what if I had chosen one of the other rays? I would get a different path for the ray bouncing around inside the drop and the rainbow would emerge in a different direction. So, the whole sky would be covered in overlapping rainbows! And, it actually is. But not all of these infinite rainbows have the same brightness; it turns out that at 42° the emerging light is the brightest. You can actually derive this angle of maximum brightness if you know calculus and trigonometry; see the Wikepedia article on Rainbo w. So, if you are standing in just the right place to see the colors from this drop, then all other drops which sent their rainbow in your direction will also be seen but as coming from different points in the sky. The locus of those points will be a perfect circle. If you are in an airplane it is possible to see the full circle. One last issue: it turns out that we often see a second, dimmer rainbow above the bright one. The reason for this is that some of the incident rays will reflect twice instead of once inside the drop before they come out; these form the second rainbow. I hope this is not too complicated for a five-year old, but hopefully you can digest it and explain it in terms she would understand.

QUESTION:
It says in a lot of places that wavelength is inversely proportional to frequency. Would it not be possible to increase the speed of the wave, (and therefore the frequency) so more waves pass through a point per second, without increasing the wavelength?

ANSWER:
In general, v=fλ and you can hold any one of the three constant and ask what happens to the other two. Here is a simple example: A guitar string of length L vibrating with its fundamental frequency is a standing wave with λ=2L. You can change the speed of the wave by changing the tension in the string (which is what the tuning pegs do). But the wavelength cannot change so the frequency must.

QUESTION:
Does the gravity of earth comes from molten core.and if so can we create artifital gravity by making molten core simillar to earth by rotating it at high speed.

ANSWER:
Gravity is caused by mass. The earth's core constitutes approximately 1/3 of its total mass and rotational speed has nothing to do with it. Neither does the "moltenness" have anything to do with gravity. So if you had a molten core alone, rapidly rotating, its gravitational field would be just the same as if you had a solid sphere of the same mass; there would be nothing "artificial" about it.

QUESTION:
what force are acting on a ping pong ball at the top of its bounce is there just gravity or is the kinetic energy from the ball still at play.

ANSWER:
The first thing to note is that kinetic energy is not a force. And I don't know if when you say "top of its bounce" whether if is in purely vertical motion or is in a trajectory during which it will still have a speed at the top. If it is the former, it is at rest and the only force on it is its weight (gravity). If it is the latter there will also be an air drag force opposite its direction of motion. (Air drag is quite important for a ping pong ball.)

QUESTION:
My question is about the actual energy consumption that is required to produce a certain amount of electrical output: Framing the setup for the question: If I have an electrical generator that can produce 1kw of electrical energy and I spin the armature with NO load, the amount of work I am producing to spin the generator is fairly nominal. It's simply the frictional losses of the bearings, the amount of energy to accelerate the mass of the armature to a particular rpm (lets say 1000 rpm), and perhaps some wind resistance. This will have some numerical value, I am assuming in joules or horsepower. (please correct me if I am wrong).

Now, if I throw a switch that connects 10, 100 watt lightbulbs. The back EMF is tremendous. Anyone who has tried to spin a generator by hand can attest to how difficult it is to try and light just 1 100 watt light bulb. Assuming the generator is 98% efficient; how much work (or energy) is required to produce the 1kw of electricity to light the bulbs? I would like to compare the "NO LOAD" power requirement to spin the armature to the "FULL LOAD" requirement to spin the armature.

ANSWER:
I don't think there is much of a mystery here. Let's forget about your first paragraph because when you say 98% efficient, that presumably includes all the losses you enumerate. This generater can generate 1 kW of power at 1000 rpm. Now you are asking it to give you 1 kW if you attach 10 100 W bulbs. You ask how much energy you have to put in but that is not the right thing to ask; you should ask how much energy per second (Watts) you need to supply, power. Since the efficiency is 98%, you need to put in 1 kW/0.98=1.02 kW of power.

QUESTION:
Hello, i was curious why science hasn't utilized the physics of "slipping" into generating energy... I understand there are road blocks, but is the potential of slipping to generate energy not extreme enough to warrant overcoming them? Can you not generate a lot of energy with slipping? or is it just that in comparison to other forms of generating energy, it just doesn't compare and it's not as exponentially capable of generating energy as im assuming. Like when i imagine moving a large object at high speeds once you've propelled it to the speed you want it wouldn't the physics of slip, give it the continuous push it needs to maintain or even exceed the level you had put it too..and would not the physics of slipping then take over the propelling of the object...and if we could create or find..a suitable force that creates slip and resists wear and tear long enough to warrant using would that not enable us to drastically improve our capacity to generate energy??

ANSWER:
I presume you mean friction? Friction generally takes energy away from a system. For example, a box with kinetic energy sliding across a floor stops because friction takes the energy away from it. That energy which the box had does not really disappear but shows up as heat (the floor and box will get a little warmer) and sound (while sliding you can hear it). Are you suggesting that we could use the heat and sound energy somehow? Why not just use the energy the box already had? Usually we try to eliminate friction as much as we can to maximize other sources. One example is the brakes of a convential car which transform all the kinetic energy of the car into heat; electric and hybrid cars use magnetic induction to put that kinetic energy into the batteries rather than into heat in the drums or disks of brakes.

QUESTION:
Hi, today I read an article on Armstrong Limit and I have a question about it, if saliva/tears boil in 36 degrees Celsius in the Armstrong Limit why is it a problem, does it cause any health issues?

ANSWER:
Your body is about 60% water. How could you ask if it would be any health issues if all that water started boiling?

QUESTION:
If you could dissassemble a human atom by atom, and then store the human in his or her dissassembled atom state, could you reassemble said human in the future without them aging essentially creating some form of atomical time travel? Also if it were achievable, would they retain their conciousness, memories and all that?

ANSWER:
The answer is no. To read a discussion of the physics of the impossibility of the "beam me up Scotty" problem, I suggest The Physics of Star Trek by Lawrence Krauss, HarperCollins Publishers, 1996.

QUESTION:
I am wondering the following;
1. Will the electron of atoms always apear when looked for in its cloud, or can it sometimes be "missed"?
2. Will it actually only be in two places at once or could it be where ever it is looked for simultaneously?
3. Is the "quality" or "strength" of an electron compromised when seen simultaneously in its different locations?

ANSWER:
The problem with your questions is that you have the idea that you can even talk about the electron being at any particular position. All you can know, until you make a measurment, is the probablity of the electron being in any particular arbitrarily small volume. A measurement means that you look at a particular small volume and if the probability of finding it there is 1% you will only see it once every 100 times you look there. It is never in two places at the same time, it is really smeared over all places until you observe it and then it is where you observe it to be. It can never be observed at the same time in two places; otherwise there would mysteriously be two electrons even if you know there can only be one.

QUESTION:
I have a potentially unusual question to which I am currently unable to find an answer and I thought that you may be able to help. I was riding my motorcycle today and turned a corner and the front tyre came into contact with a large patch of gravel on the surface of the road. I had touched the front brake immediately prior to this and, as the front tyre hit the gravel the bike began to slide and to pitch sideways. I put both feet on the ground and steadied the bike, effectively holding it upright and avoiding a spill. Now for the question: My body is very sore after around 5 hours after the event and this has made me wonder what kind of energy did I absorb in my attempt to avoid the accident? The bike weighs 220kg, I weigh 125kg, I was travelling at 20mph (after I had released the brakes )on relatively flat ground and stopped the momentum of the bike within 2.5 yards (after I had released the brake). I am completely unable to fathom a calculation for this, I’m afraid . Can you help me at all?

ANSWER:
So, we have m=345 kg moving with a speed v=20 mph=8.94 m/s and stopping in d=2.5 yd=2.3 m. The initial kinetic energy was E₁=½mv²=2.73x10⁴ J and the initial linear momentum was p₁=mv=3.08x10³ kg·m/s; the final energy and momentum are zero. Change in energy is equal to work done, so W=-E₁=-Fd=-2.3F where F is the average force exerted by the ground on you (frictional drag); so F=1.19x10⁴ N. You could also say that the change in momentum equals the Ft where t is the time to stop, so t=1.19x10⁴/3.08x10³=3.86 s. The average acceleration over the stop was F/m=34.5 m/s², about 3.5 times the acceleration due to gravity, 9.8 m/s². So why were you so sore? Because Newton's third law says if the ground exerts a force on you, then you exerted an equal but opposite force on the ground. So you were exerting a force on the order of 10,000 N, about 2000 pounds, for about 4 seconds. That sounds like an awful lot to me. You said the brakes were not engated as you traveled 2.5 yards but was the bike skidding sideways? That would have been like having your brakes on and have lessened the amount of force you needed to apply to stop the ride.

QUESTION:
My question is about Newton's 3rd law. I understand it pretty good, so I'm making myself questions trying to understand the limits. Here is my question. Let's suppose I'm in a target range, shooting at the target. Obviously the bullet go through it. In the very precise instant that the bullet hit the card, how can that be explained by the 3rd law. Is there an opposite force, equal in magnitude, opposite in direction, even though the bullet go through the target?

ANSWER:
During the time the bullet and target are in contact with each other, the bullet exerts a force on the target; this force is evidently stronger than the target can withstand and that is why it tears and the bullet passes through. Now, when that is happening, Newton's third law states that the target exerts an equal but opposite force on the bullet. It is not very hard to punch a hole through a sheet of paper, so the force is not very big in this situation; nevertheless, the bullet feels that force and as a result emerges on the other side with a slightly smaller speed. If you had 100 sheets of paper to make your target, the bullet would be going with a considerably smaller speed when it came out the back; with a thick or strong enough target the bullet would just stop in the target.

QUESTION:
In this video, starting at 2:00, a pair of 2-liter bottles suspended over 2 loudspeakers are made to orbit about a fulcrum on which they are balanced when excited at their resonant frequency purely by sound waves. But such wave motion is back and forth, so how can it impart momentum in just the forward direction? I must know how this works!

ANSWER:
Yes, the pressure at any point in the bottle, including the open end, will fluxuate with the frequency of the air in the bottle. When the pressure is low, air from the outside is sucked into the bottle; when the pressure is high, the air is pushed out. But the two air motions are not analogous. As shown in the figures below, when air flows in it comes from many directions so this gives the bottle only a small thrust to the right. But when it flows out, the neck tends to align the air motion causing a larger thrust to the left.

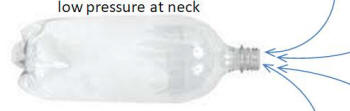
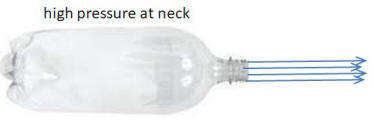
A cavity with a narrow, open neck at one end is called a Helmholz resonator.

QUESTION:
Einstein's theory claims that a large object in space will create a gravitational field that will bend Space-Time. My question is - if indeed a large body like the Earth does create a bend in Space-Time do we exist in another aspect of time than that of the surrounding space which is empty and thus does not have a gravitational effect on that around it?

ANSWER:
The rate at which clocks run depends on the intensity of the gravitational field. A clock 100 m above you runs at a different rate as yours. So I guess you do "exist in another aspect of time" (whatever that means!) from any region where the magnitude of the gravitational field is different than yours. This effect is often referred to as the gravitational red shift. It turns out that gps systems must correct for this effects since timing between you and satellites at high altitudes must be extraordinarily accurate. I should note that the differences in time are extremely small, even for something as large as the sun which is incredibly massive.

QUESTION:
If at the start of the universe all the matter was within a cubic meter how didn't it create a black hole

ANSWER:
I state clearly on the site that I do not normally do astronomy/astrophysics/cosmology, so take with a grain of salt that I am no expert. I would guess that there is so much energy in this cubic meter that whatever forces might be acting are simply inadequate to reverse the expansion. Also, I used the word "other" because we do not know what the laws of physics were in the very young universe.

QUESTION:
got a discusion with a friend, about the riding wind versus side wind. when driving, the air thats in front of the care needs to move, and puts presure on the car. does that increase when you drive harder, and will a side wind have more or less effect when you drive harder?

ANSWER:
If you are driving into a headwind there is a force back on you due to the speed of the wind. You would therefore have to press harder on the accelerator to keep going with the same speed you would go in still air. But that does not have a handling the car, merely holds you back causing you to use more gasoline. For example, if your car has a speed of 60 km/hr into a 20 km/hr headwind, it would be the same as driving 80 km/hr in still air. In a crosswind, however, handling is more of an issue. There is a tendency to push the car in the same direction as the wind is blowing; if the road is wet or icy and the wind is strong enough, the friction of the tires could be inadequate to keep you from sliding across the road. Even if the road is dry, the tendency for the car to turn with the wind and you need to slightly steer into the wind. Also keep in mind that a strong headwind will not necessarily keep blowing exactly opposite your direction or else you may need to do a maneuver where the wind now is partly blowing across your path. So, always be extra careful on a windy day.

QUESTION:
I respect that Heisenberg's Uncertainty Principle can't be violated. . But a daily lab event seems to say "no you can". Here's the situation. Take the cathode ray tube in an oscilloscope. An electron is ejected from the cathode, deflected by coils around the tube's neck and then impacted at a precise screen location. The UP says I can never accurately know the electron's position and momentum at T. But I do accurately know P, it's relativistic mass is constant and so is it's velocity. In order to place that electron at the precise point on the tube face, the circuit must know its exact location to know when to increase voltages to the neck coils for proper deflection. Why is this scenario not a violation of UP?

ANSWER:
Well, how accurately can you actually know P? Certainly not better than maybe 0.1%. And position? Maybe to a micron or so. But, the P you are talking about and the position you are talking about are not the proper quantities to be talking about in terms of the UP. Suppose we call the line between the electron gun to the center of the screen the z-direction. Then the UP is ΔzΔp_z≥ℏ but the position on the screen would be perpendicular to z, could be either x or y,and ΔxΔp_z has no uncertainty principle associated with it.

QUESTION:
So I'm in high school and I'm in physics. I'm also a musician (piano, singing, etc.). I was wondering about pendulums, but specifically metronomes. If I wanted to use a metronome as a model in an energy conservation project, would I simply apply the same rules as normal pendulum situations? I guess I'm just saying that I'm having trouble with the difference between metronomes and other pendulums. I tried to find the answer online, but whenever a metronome is used in a physics example is always is talking about simple harmonic motion or synchronizing metronomes, which isn't really what I'm asking. I'm not advanced enough yet to figure out the physics behind a metronome by myself, either. Sorry about the long paragraph for what's probably a pretty simple question! I'm basically just asking if, when discussing energy transfer/conservation, work, and force in physics does a metronome abide by the same rules as a normal pendulum, and if not, how does it differ?

ANSWER:
A metronome is certainly not a simple pendulum which is basically a weightless stick of length L frictionlessly pivoted at one end and attached to a point mass m at the other end; the point mass oscillates below the pivot. As you have probably learned, this seemingly simple problem cannot be solved analytically but can be approximately solved is the angle is small. The result is that the frequency f (cycles per second) is approximately f≈[√(g/L)]/(2π) where g is the acceleration due to gravity. Note that the mass does not matter, a bit of a surprise perhaps.

Now the metronome is clearly not a simple pendulum because the mass is above the pivot point. But, how can that be? If you just stuck a mass on the end of a stick and rotated the mass to a point above the pivot, would it oscillate about the very top? Of course not, it would still oscillate about the very bottom but with an amplitude which was very big. So, how does the metronome do this? Well, I have earlier worked out how a pendulum works. You may want to have a look at this but, being in high school you probably are not ready for the math there. And maybe your physics class has not even gotten to rotational motion yet so you would not know about moment of inertia, angular acceleration, etc. But you find out the nature of the pendulum in a metronome: there is a bigger mass below and out of site. So this is really a "double pendulum" and as long as the hidden mass is bigger, it (the bigger) will oscillate about the bottom while the smaller oscillates about the top. The picture here of the metronome made of plexiglas shows that bottom mass. You can also get the final answer if the "stick" has negligible mass compared to the two masses, f=ω/(2π)=[√(g(ML_M-mL_m)/(ML_M²+mL_m²)]/(2π) where M (m) and L_M (L_m) are the mass and distance from the pivot of the lower (upper) weight.

Now to your question, whether energy conservation applies to a metronome. No real-world pendulum as its mechanical energy conserved because friction of some sort is always present. However, if you put it in a box from which no energy can come in or go out, the total energy will be conserved, even if the pendulum stops, the air in the box will heat up a little bit and if you were to measure all the energy contained in thermal energy you would find all the energy which the pendulum originally had. So the answer to the "basically just asking" is yes, the two pendula "abide" by the same physics rules. Also note that there is a little spring-driven motor you can see inside; when you wind it up you do work to give it potential energy and it then gives this energy to the pendulum to replace energy lost to friction.

QUESTION:
Let's consider crushing some item with scissors blade. It is easier to do it when the item is positioned closer to the pivot(assuming the force of squeezing the scissors is constant). I am asking to check the following explanation: Is it so because to avoid being crashed the item must generate reaction force impacting the blades of such magnitude that the blades are not moving(theirs torques have to equal zero).Let's assume that force momentum coming from squeezing the scissors is constant(we don't change force of our fingers nor the distance from the pivot) and potential of generating reaction force by the item also. Then the only thing we can do to decrease this torque coming from reaction force(and therefore making the item less "resilient") is to shorten the distance between item and pivot. My wonder is if it all comes down to considering movement of scissors blades around axis, meaning: blades are moving the item gets crushed, blades are still(torque equals 0) the item is in one piece.

ANSWER:
You can understand the principle by just considering one half or the scissors; then the other does just the same but with opposite forces. All your talk about "reaction force" is wrong; look at my diagram—the force labelled F₁ is the force your thumb exerts on the scissor and the reaction force is the force which the scissor exerts on your thumb which is the same magnitude but oppisite direction. I will assume that there is some small object you want to "crush" located somewhere along the blade. This gets a little confusing, so read the next sentence carefully. If you exert the force F₁on the scissor and the scissor is not closing, the sum of the torques exerted on the scissor must equal zero; if the object is located near the pivot, like where F₂ is, the object must exert a force opposite to F₂ but of the same magnitude since F₂is the force the scissor exerts on the object which is what you are interested in. (Ignore F₃ for now.) To calculate the magnitudes of the torques you need to multiply the force times the moment arm (yellow lines). The moment arm for F₁ is much longer than for F₂ and therefore F₂ should be much larger than F₁. Now, consider placing the object out near the end of the blade where F₃ is drawn; its moment arm is larger than for F₁ so its magnitude is smaller. I hope it is now clear why placing the object closer to the pivot results in a larger force on it than farther away.

QUESTION:
I have a question about the weak nuclear force. Why do we call weak force a force? All what's said about the weak force is that it cause decays by changed one particle into another (or at a fundamental level, by changing the flavour of quarks). But , "what makes it a force?" Do we call it a force only because it involves W/Z bosons or there's something else.

ANSWER:
It is better named the weak interaction. The concept of a force is generally not useful in quantum physics, but, since we all have a gut feeling what a force is in macroscopic classical physics, it is natural to think of interactions between objects as resulting in forces. But, to treat interactions between objects quantum mechanically we use the concept of fields to describe those interactions; fields are also used in classical physics as well—think electric, magnetic, and gravitational fields. At the quantum level fields alone are useful, not forces. And when you have a field it can be quantized and the quanta are often viewed as the "messengers" of the field; the field quanta are photons for the electromagnetic field, gluons for the strong interaction, and W^± and Z bosons (as you note) for the weak interaction.

It is interesting that the fourth "force" in nature is problematical: no one has successfully quantized the gravitational field and achieving that is one of the holy grails of physics.

Also interesting is that the notion of force is not useful in the theory of special relativity because the usefulness of force depends on the usefulness of acceleration. At high speeds where special relativity is important, different observers will see different accelerations for the same object; if we think of force in terms of Newton's second law (F=ma), different observers would deduce different forces. If, instead, we thought of Newton's second law as force equals time rate of change of linear momentum, force could be invisioned but only if linear momentum (mass times velocity) were differently defined. But I digress...!

QUESTION:
I am a 180 lb man competing 180 lb weight class five time world champion powerlift. I bench 500 lb and I would like to know how much force am I executing to lift 500 lbs?

ANSWER:
To hold 500 lb at rest or to move 500 lb straight up with constant speed requires a force of 500 lb. Since the weight you lift is initially at rest and momentarily at rest when your arms are fully extended, you must exert a force larger than 500 lb to get it started moving upward and smaller than 500 lb for it to stop at the top. I have watched videos of the bench press and it appears that during most of the time the bar is moving with a constant speed; so most of the time the force you exert is about 500 lb. To do a rough calculation of the force necessary to get it moving, I will use a total lift distance of about 1 m in a time of about 1 s so the speed is roughly v=1 m/s; 500 lb has a mass of about m=227 kg. (I will use SI units, like scientists prefer, and convert back to pounds in the end.) Suppose that the time it takes to accelerate the bar to 1 m/s is t=0.1 s; so the acceleration is a=(1 m/s)/(0.1 s)=10 m/s². So the force F you must exert is calculated using Newton's second law, ma=(F-W) where W=mg is the weight of the bar and g≈10 m/s² is the acceleration due to gravity; F=227(10+10)=4540 N=1000 lb, twice the weight you are lifting. Similarly, if it takes 0.1 s to stop the bar, the force you would apply would be F=227(-10+10)=0, the weight will stop itself because of gravity. Keep in mind that these are estimates using reasonable numbers; the actual numbers depend on the way the individual does the lift.

MY ANSWER IS WRONG, OR AT LEAST INCOMPLETE. SEE BELOW

QUESTION:
Recently when cleaning, I opened the cover of our ionisation smoke detector, as I was opening the smoke detector cover, dust fell from the inside of the smoke detector into my eye. The whole inside of the cover was covered in this dust-a brown colour dust, not grey colour. I was concerned that this dust has been given off by the Americium due to the slats on the ionisation chamber which allow particles to escape from the radiation. Could this be so? I was concerned as it said online that it was dangerous to ingest or inhale the americium from smoke detectors and this dust entered my eyes?

ANSWER:
I have recently answered a question about smoke detectors; you should read that. The americium is in a sealed container and cannot get out. Also, the color of dust depends on where it comes from. There is probably some source of brown dust in your house and you wouldn't notice its color except when something like your smoke detector accumulates a relatively large amount over a long time.

CORRECTION:
I received an email with additional information about which I was not aware. Essentially it said that the recoiling americium nuclei could collide with and eventually damage the casing around the source. Since your smoke detector is 27 years old and the rule of thumb is that the useful lifetime of americium smoke detectors is about 10 years, you should dispose of this one and get a new one. (Use the recommendations of the answer you included in your question to dispose of it safely.) I still believe that you need not obsess over the small exposure you received when you were cleaning, given the very small numbers I quoted in the earlier answer about smoke detectors; the unit quoted there, rem (Roentgen equivalent man), is specifically meant to indicate exposure to ionizing radiation of human tissue and is therefore more useful than Curies used by the author of the answer which just measures the amount of radiation emitted without consideration of their health effects.

QUESTION:
A piece of cork is thrown vertically downwards from a sky scraper 300 meters high. Its initial velocity is 2 m/s. Air resistance produces a uniform acceleration of 4 m/s² until the cork reaches a terminal velocity of 5 m/s. Why does the cork reach terminal velocity?

ANSWER:
There is something terribly wrong about this question. I see only two ways I can interpret this question.

I can interpret everything completely literally as written. Of course, this cannot be physical because the air resistance F_A must depend on the speed v (usually F_A∝v²) of the cork and it will certainly not, in the real world, result in an acceleration which is constant. If the mass of the cork is m, then F_A=4m; there is also the force of gravity F_G=-mg where g=9.8 m/s². So the net force is F_net=ma_net=m(4-9.8)=-5.8m, so a_net=-5.8 m/s². So the cork will fall with a downward acceleration of magnitude 5.8 m/s² and never have a terminal velocity since it just keeps speeding up.
Maybe you didn't really mean to say it has a "uniform acceleration" but that F_A=kv² at the instant you release it with speed down of 2 m/s and the acceleration due to that force is 4 m/s²; so k(2)²=4m or k=m. Now we have F_net=ma_net=(mv²-mg); when v=√g=3.13 m/s, a_net=0, so if this is the interpretation of the problem, the terminal must be 3.13 m/s, not 5 m/s.

I cannot think of any interpretation of this problem which would be self-consistent.

QUESTION:
How much energy in joules would it take to propel an object with a mass of 14 grams to a speed of 1.25 kilometers per second over the course of 0.15 seconds? Further, how much power would it take to create this amount of energy? I know this sounds like a homework question, but it isn't. this is a question from someone who barely understands any of these physics terms and who has hardly any idea how to calculate the simplest of formulas, yet is trying to get a concrete idea of what it would physically require to complete this hypothetical task.

ANSWER:
I think it is a homework question and you are trying to pull the wool over my eyes; nobody just wonders how much energy a 15 gm object going 1.25 km/s has. I will outline what you need to solve, but just this once and not in complete detail.

The kinetic energy E of an object with mass m and speed v is E=½mv². If you want the energy to be expressed in Joules, m must be in kilograms and v must be in meters per second. If the object takes a time of t to achieve an energy E, the average power expended to do so is P=E/t. If you want the power to be in Watts, E must be expressesed in Joules and t must be expressed in seconds.

QUESTION:
If a full cart is pushed at the same time as a empty cart with the same force witch one will stop in motion first? And why?

ANSWER:
I assume that the carts are identical except for the loads; and that the force "does the same thing" to both of them. The heavy cart has mass M, the light cart m. There are two ways you can apply the force F:

Push over the same distance d for each. In that case you give the same kinetic energy to each, ½MV²=½mv², so V=v√(m/M) where V(v)is the starting speed of M(m). Note that, as you would expect, v>V.
Push for the same time for each. In that case you give the same linear momentum to each, MV=mv, so V=v(m/M). Again, v>M but by a different factor.

Now, what stops the carts? Friction f which is proportional to the weight of each car. For the loaded cart, f_M=-μMg and for the empty cart, f_m=-μmg ; here the negative sign indicates that the force is slowing the cart down, μ is the coefficient of kinetic friction, and g is the acceleration due to gravity. Because of Newton's second law, the accelerations of the two cars are A=f_M/M=-μg and a=f_m/m=-μg. Because the accelerations of the two cars are the same, the one which started fasted (empty) will go farther and take a longer time to stop.

QUESTION:
My question is hypothetically ( or exactly ) does or would an "alien" be able to negotiate a 90 degree turn and not be splattered on the inside of the vessel.??

ANSWER:
That would depend on two things. First how long does it take the vessel to turn which would determine the average acceleration? Second, what is the physiology of the alien, in particular how much acceleration can her body endure?

QUESTION:
Can you please explain why Magnetic force is Non-Central when the Electromagnetic forces are Central forces? On the same note, Why is the friction non conservative when the EM forces are considered conservative in nature?

ANSWER:
You have some misstatements here. For "central" I think you mean conservative because, for example, the electric field for a uniformly charged wire does not all come from a single point (which is the definition of central fields). Also, when you say "electromagnetic" I think you mean electric. Now, the force due to a static electric field is conservative, but not all electric fields are conservative. For example, the electric fields induced by changing magnetic fields are not conservative. You ask why the magnetic force is like it is—because that is the way nature is. Be aware that electric and magnetic fields are manifestations of one field, the electromagnetic field, and not separate fields but intimately linked. Regarding why friction, admitedly due to electromagnetic forces, is not conservative, I refer to the first part of this answer where I emphasized that there is no reason to assume that electric or magnetic forces are conservative.

QUESTION:
If black is the absence of light, and thus of color, how is it one can mix primary colors together to get black paint?

ANSWER:
Because mixing paint is not the same thing as mixing light. It makes sense simplistically: red paint absorbs everything but red, blue paint absorbs everything but blue, so red+blue paint absorbs everything—black. Like I said, this is simplistic because they are not purely red nor purely blue, but it gives you an idea of why mixing paints would look black.

QUESTION:
Can something rotate if it is not symmetrical?

ANSWER:
Yes. It is easiest to visualize an object of any shape you like which is in empty space at rest. You now give it a kick somewhere on its surface. Unless the direction of the force is directed directly at the center of mass, the kick will cause the object to move away from you and be also rotating as it moves. The rotation will be about an axis which passes through the center of mass. You could make the object rotate about any axis you wanted but you would have to hang on to the "axle".

QUESTION:
Do we know how a nucleus of an atom is structured with its protons and neutrons? Is it merely a discombobulated mess, or is there actual structure to it? Are they in movement within that space between itself and the electrons (spinning, rotating, doing a disco dance, etc)? This question has been on my mind for a while and I cannot find any resources on it, and graphical 'representations' just show a mass of random protons/neutrons.

ANSWER:
I will note at the outset that this question is in violation of site ground rules: "…single, concise, well-focused questions…" Nuclear structure is an entire subsection of physics and it would take a whole book to give you even an overview. I spent my entire research career, more than 40 years, studying nuclear structure. The answer is that it is not "merely a discombobulated mess" but pretty well understood. I will give you a few examples.

The force between nucleons (neutrons and protons) is very strong and results in the nucleus being extremely small compared to the the atom (nucleons and electrons). The size on an atom is on the order of Angstroms (10^-10m) where the nucleus is on the order of femtometers (10^-15 m). If the atom were about the size of a football field, the nucleus would be about the size of a golf ball.
One of the first successful models of the nucleus was the shell model. Because of the average force due to all the other nucleons, each nucleon moves in orbitals like electrons do in atoms under the influence of the Coulomb (electric) force.
A later, also successful, model is the liquid-drop model where the particles all move collectively. Imagine a liquid drop which, when bumped will oscillate in some way. Or imagine a nucleus which is deformed like an American football. It could rotate about its center of mass. Many heavier nuclei have rotational band structures. In these cases the nucleons all move in choreographed unison, maybe more like a line dance than a disco dance.

Hope this gives you the idea that structure of nuclei is fairly well understood. The examples I give are over simplified because, among other things, when inside a nucleus, nucleons lose their individuality.

QUESTION:
I was recently doing an OCD Exposure homework and now I am unsure of what I did. I opened the smoke alarm cover and touched around all the inside parts of it. I touched all the sides of the outside of the ionisation chamber with the radiation symbol on it for around 5-6 minutes. I did not open the ionisation chamber. I want to find out
1. Did this expose me to a lot of radiation?
2. Will this increase my risk of taking cancer in the future.
Can you please tell me honestly, even if it is not what I want to hear, I just need the facts.

ANSWER:
The radiation from smoke detectors is trivially small. Even if you had removed the source and kept it around it would have given you negligible radiation exposure. A study by the Nuclear Regulation Commission showed that "…a teacher who removed the source from a smoke detector could receive a dose of 0.009 millirems per year from storing it in the classroom. The teacher would get another 0.001 mrem from handling it for 10 hours each year for classroom demonstrations, and 600 mrem if he or she were to swallow it…" To put this in perspective, you receive approximately 2.2 millirems per year from natural sources (from space above, ground below) if you are at sea level, even more if you are above sea level. Don't swallow it, though!

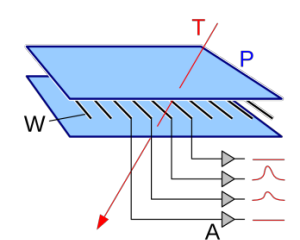
QUESTION:
I have a question about the operation in drift chambers. Charged particles enter the chamber medium to ionize the gas atoms. The electric field is applied to drift resulting electrons and ions. Also, there is a magnetic field applied to measure the particle momentum. However, all the papers use the Lorentz force on the charged particle to calculate its momentum in this form F= qvb and don't include the force due to the electric field. In other words, why the electric field doesn't have an effect on charged particles entering the drift chamber?

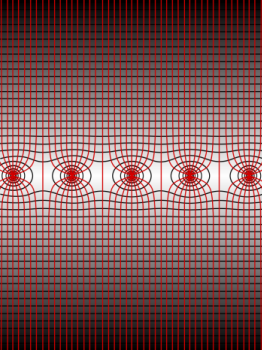
ANSWER:
The figure above shows a schematic sketch of one layer of a wire chamber. The particle ionizes atoms near wires it passes close to. The wires carry a charge which creates an electric field near them which then collects charged particles and sends a pulse to a computer. The electric field is fairly strong near the wires but quickly becomes nearly zero in a very short distance distance from the wires. Shown in the second figure are equipotential lines due to the voltage on the wires; note that at distances about equal to the wire spacing the equipotentials are constantly spaced indicating nearly zero fields. A second consideration is that the particle being detected has an extremely large energy which makes electric fields of the magnitude near the wires practically invisible to the detected particle.

QUESTION:
We know that our universe has fine tuned gravity constant so my question is can a universe born with a different gravity constants other than fine tuning or there is no possibility other than fine tuning constant

QUERY:
This is a very deep question, and you greatly underestimate the situation. In fact, the properties of a universe are extremely sensitive to the values of many fundamental constants, not just G. So you cannot just think of how things would change if G were changed. Usually the question is not about whether a universe could be "born" if the fundamental constants were different (partly because we really do not know the mechanism of the big bang); rather, the question is usually "how much could we change the fundamental constants and still have a universe where life is possible?" Here is an interesting example I read about of the consequences of changing fundamental constants: If the strong nuclear force were increased by 2%, the diproton (two protons bound together) would be possible. The consequence would be that stars could not exist because the proton-proton cycle which produces the energy in stars would not occur if two protons could just stick together.

QUESTION:
We know from Maxwell equations that c = 1/(e0m0)1/2 which indicates that electromagnetic fields propagate in vacuum with the speed of light. Thus, light is an electromagnetic wave as proved later by Hertz. Consequently, Can induced electromagnetic fields change the energy carried by light waves if they were exposed -in a certain way- to them?

QUERY:
It is not clear what you are asking. "...in a certain way..."?

REPLY:
Would light interact with electromagnetic fields or not?

ANSWER:
Yes, light will interact with any electric or magnetic field. First, there is the superposition principle; at any time and place the net electric or magnitic field is the sum of all fields from all sources. Here is another example how "light" can interact with an electric field: a photon with sufficient energy, if it passes close to a nucleus where the electric field is particularly intense, may convert into an electron/positron pair.

QUESTION:
I ride motorcycles and do have BS degree in Biology and am familiar with simple physics. There is a new airbag technology that has been recently released to consumers. This technology was initially developed for motorcycle racers close to 15 years ago. The early tech used a cord attached to bike and rider, when the rider and bike were separated the airbag deployed. Due to advancements in electronics new system use a small computer with appropriate algorithms sensors to determine when a crash is happening and activate the airbag. This technology is now available to consumers like myself at reasonable cost $700-1,100 + for a system. The European Union has developed standards for impact protection pads for motorcyclist's. EN 1621-2:2014 defines the exact spinal pad impact reduction capabilities, standards and testing requirement's. I have found it difficult to find technical data on the new airbag system with regard to exact impact reduction capabilities. What I have found is that rider report being in a crash with the airbag system and it registered a IMPACT force of 18 G-forces. The rider was not injured. Assuming that the rider suffered a TRANSIMTED force of the no more than 12kN (as per the EN 1621-2:2014). How much energy in Kn did the airbag system absorb ? What is the energy absorption capability difference between the airbag and a EN 1621-2:2014 pad with 12 kN transmitted energy ? Problems
1) I have been unable to determine the EN 1621-2:2014 IMPACT test force, I only know the TRANSMITTED test force is no greater than 12kN
2) Rider crash data uses G-force to measure IMPACT force, and provided no transmitted force data, due to there being no injury, I feel it safe to use a transmitted force of 12 kN .
3) Some forces are given in kN and some G-forces, I do not understand the difference of these force measurement systems and I do not know how to correctly convert from one measurement system to another to solve my problem

ANSWER:
I am sorry, but your question violates one of the rules of the cite, "...single, concise, well-focused questions..." I can, however, help you with the single question of confusion between kN and g-force. The g-force is technically not a force at all, it is an acceleration. As you likely know, the acceleration due to gravity is g=9.8 m/s². The g-force is usually expressed in gs; for example, because of some force you experience an acceleration of 10 gs, so that means that if your mass is 100 kg, the force you experience is F=ma=100x10x9.8=9800 N=9.8 kN.

QUESTION:
I was wondering at sea level, given variable air densities. What is the rate at which a human would slow in relation to the earths rotation if suspended in the air for an extended length of time. If you were able to nullify the air density acting on your body could you theoretically travel the globe at 1000 mph opposite the earths rotation. Am I forgetting variables other than loss of contact with the earth and air density? I know that inertia would keep you moving with the earth however you would begin to shed that inertia quickly correct?

ANSWER:
Any way you could be "…suspended in the air…" would rely on something attached to the earth. Even a hovering helicopter is being held up by the atmosphere which rotates with the earth. No, you cannot travel around the earth by staying still.

QUESTION:
Why does a volume of any random-motion particles begin spinning when it is compressed, either by outside force, or by gravity? Why they heck do things go into a spin? Is this some form of conservation of momentum?

ANSWER:

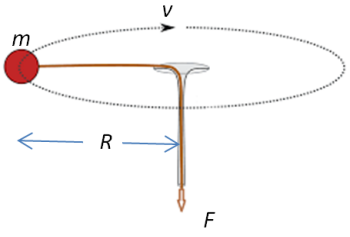The things do not "go into a spin", they were already spinning but more slowly, perhaps too slow to notice. It is, indeed, because of a conservation principle, the conservation of angular momentum. The principle states that if there are no external torques acting on a system of particles, the angular momentum will remain constant. Let us take a very simple case, a single point mass moving with speed v in a circle of radius R. It is attached to string which passes through a hole in the table; you are holding it in its orbit by pulling down with just the right force F (which happens to be F=mv²/R, but we don't need to know that now). Its angular momentum is equal to L₁=mvR. Now you pull down with a bigger force so that the new radius is R/2; as you did this, no forces on m exerted any torque so the angular momentum was conserved. L₂=mv'R/2=L₁=mvR, so v'=2v., spinning faster than before your force pulled it in. But, you argue, if there are many particles with random velocities there is, surely, for each particle a second particle which is rotating in the opposite direction so the net rotation is zero. But, this argument will only work exactly if there are an infinite number of particles. In a very large assembly of particles even a very small difference between a pair of particles can cause a large angular momentum if they are far away from the center of mass of the assembly.

QUESTION:
What is the terminal velocity of a 5 inch hail stone, and how many psi would be necessary to launch that roughly 1.1 pound ball of ice down a barrel style tube? I'm looking to do some stress testing on some roofing material simulating the most severe weather.

ANSWER:
I have a good way to estimate the air drag force at atmospheric pressure: F=¼Av² where F is the force in Newtons, A is the cross sectional area in m² of the object, and v is the velocity in m/s; you must work in SI units because the factor ¼ contains constants like drag coefficient, density of air, etc. Now, F=ma=¼mAv² where a is the acceleration. The hailstone has a downward force on it, its weight mg where g =9.8 m/s² is the acceleration due to gravity; when v gets big enough that the drag force (upwards) equals the the weight down, the acceleration becomes zero. This leads to the terminal velocity v=2√(mg/A). I calculated the mass to be about 0.74 kg=1.6 lb and the area about 0.0167 m², so v=48 m/s=107 mph.

Regarding the cannon you want to make, you cannot just know the psi but the distance over which the force from that pressure will act. If you want to push it with a force F over a distance d with a pressure P, you will (ignoring any friction) give it a speed v=√(2Fd/m)=√[2PAd/m] where m is the mass of the projectile and A is the cross sectional area of the tube. So, you can either push it with a big pressure over a short distance or a small pressure over a long distance. Let's use the number I used above, m=0.74 kg, A=0.0167 m², and use a d=2 m long tube; then v=48 m/s, 48=√(2xPx2x0.0167/0.76). Solving, I find P=2.83x10⁵ N/m²=41 psi. Don't forget that there is atmospheric pressure, 14.8 psi, on the front of the ball so a rough estimate would be 56 psi. The actual required pressure would be quite a bit larger than this because friction (including air drag) would not be negligible.

QUESTION:
When actors are shot off of roof tops, why do they fall forward when the bullet should propel them backwards?

ANSWER:
I have already discussed this question in some detail. The bottom line is that when a bullet hits a man the recoil is negligibly small.

QUESTION:
i have come up empty in trying to figure out a certain issue .. I am doing a project with air cylinders and need a calculation based on how much compressed air would be in a cylinder thats 2 x 6 inches and yes i searched google and YouTube and there is mention on these but it appears different folks have different formulas and different conclusions... i am startled because of the lack of information on this, i wouldn't assume this would be THAT elusive.. most answers I got was - P1 x v1 = p2 x v2 formula and that seems something i will learn at one point in time after i learn the basics but here is what i got so far if i may- Pressure times volume divided by atmospheric or : P x V / 14.7 .. seem ok at first when i calculator a pressure of 40 psi times the volume of my cylinder being 18.85 Cu inch then divided by 14.7 atm which comes to 51.3 Cu inch...but if i change 40 psi to 10 psi things get hairy... 10 (psi) x 18.85 (volume) / 14.7 (atm) = 12.82 Cu inch.. but this is less air than regular atmospheric pressure .. so the formula must be faulty

ANSWER:
The relation P₁V₁=P₂V₂ (called Boyle's law) which you state is correct provided that the temperature and the amount of gas inside the cylinder do not change. But then you do not apply it correctly. I take it that you are not adding air to the cylinder but are compressing the air in the cylinder. I am also assuming that the cylinder has a height of 6 in and a radius of 1 in and that so the volume is V₁=6x3.14x1²=18.8 in³. I also assume that when the cylinder is at 18.8 in³ there is 1 atmosphere of pressure, P₁=1 atm=14.7 psi, so P₁V₁=276 in·lb. We now have that V₂=276/P₂; if P₂=40 psi, V₂=6.90 in³; if P₂=10 psi, V₂=27.6 in³. Notice that for the 10 psi case the volume is bigger than the the original volume because the pressure is smaller than atmospheric pressure. If you can't make the volume any smaller than 18.8 in³, the only way to reduce the pressure is to remove some gas or cool it. If you are interested, the most general expression for an ideal gas is PV/(NT)=constant where T is the absolute temperature and N is some measure of how much gas you have.

ADDED THOUGHT:
Rereading your question I am thinking that it is not a cylinder with a piston but maybe of constant volume 18.8 in³. In that case, keeping V and T constant, the appropriate relation would be P₁/N₁=P₂/N₂ or N₂=P₂N₁/P₁. Suppose we call the amount of gas you can put in the cylinder at atmospheric pressure 1 gas unit. Then if you fill the tank with 10 times atmospheric pressure, you will store 10 gas units.

QUESTION:
Imagine a 10 m² plate of aluminum (thermal conductivity 225.94 W/mK)that is 0.1 m thick. In the center of the aluminum plate protrudes a long skinny aluminum bar that is 20 m high, 0.1 m wide, 0.1 m long. This would look like a dirt tamper. The temperature of the large plate is at 100°C and the top of the long skinny pole is 10°C. How can I calculate heat flow in this system? I certainly appreciate your help.

QUERY:
Is the plate maintained at 100 and the top of the bar maintained at 10 and you want the rate of heat flowing through the bar? Or do you want to know the final temperature is allowed to come to equilibrium insulated from the environment? And if you actually want an analytic expression for any point in the system as it is coming to equilibrium, it would require that I have the shape of the plate; this problem probably cannot solved analytically and would require a numerical solution which I am not able to do.

REPLY:
Plate is maintained at 100; top heats up but I understand that is hard to model because the rate would decrease as the top increases in temperature (eventually becoming zero when the top reaches 100). I guess I'm really interested in the heat flow if the top is at 10 (so we could imagine it is held at 10)

ANSWER:
I am going to assume that there is no heat leakage from the sides of the bar. Initially I will assume that the top end of the bar is kept at a constant 10°C, so heat flows through the bar at a constant rate. We can figure out the heat rate as a function of the temperature difference, ΔT=100-T. I will neglect any edge or geometry effects in the bar, in other words I will treat it as a one-dimensional problem where the heat flow vector in the bar is in the direction of the bar and uniformly distributed across the cross-sectional area. In that case the equation for the rate R is

R=ΔQ/Δt=kAΔT/L

where A=0.01 m² is the cross sectional area, k=226 W/(m·K) is the thermal conductivity, and L=20 m is the length. So R=0.113ΔT W. For ΔT=90, R=10.2 W. Now, if the top remains at 10°C, that means that energy at the top is being taken away at the rate of 10.2 W; since ΔT∝L, the temperature must increase linearly along the bar when equilibrium has been achieved.

TIME DEPENDENCE:
The questioner indicated interest in the more difficult problem of no heat flowing out the top end of the bar which started out 10°C. What I did was to just give the steady-state solution like you would learn in any elementary physics course. So I dug into the transient case; I learned a lot! Below I find the general solution to the heat-flow problem and apply it to the case in question, the bar starting out at 10° and ending up at 100°. I have left out a lot of details but have provided links to derivation of the 1-d heat equation and its general solution. Algebraic steps I have omitted in applying boundary conditions could be filled in by anybody interested in these details.

The one-dimensional heat equation is

∂T/∂t=c²∂²T/∂x²

where c²=k/(C_pρ) where k is thermal conductivity, C_p is specific heat at constant pressure, and ρ is the mass density. (You may find a derivation here. ) The general solution of this equation is

T(x,t)=exp(-c²s²t)[Asin(sx)+Bcos(sx)]+Cx+D

where A, B, C, D, and s are constants to be determined for the specific problem. (For a derivation, go here. Go to Section 2.2)

Suppose the boundary conditions are that (3) the temperature of the bar is at some constant value T₁, (1) one of the bar is held at a temperature T₂, and that (2) the other end of the bar (and the sides) are insulated:

T(0,t)=T₀
∂T(x,t)/∂x|_x=_L=0
T(x,0)=T₁

These boundary conditions lead to the following:

Bexp(-c²s²t)+D=T₀B=0, D=T₀
exp(-c²s²t)[sAcos(sL)]+C=0
C=s(exp(-c²s²t)[Acos(sL)])
s≠0 so C=0
A_ncos(s_nL)=0⇒s_n=½nπ/L, n odd
- T(x,t)=T₀+Σ{exp(-c²s_n²t)A_nsin(s_nx)}
∫(T₀-T₁)sin(s_mx)dx=-∫Σ{A_nsin(s_nx)sin(s_mx)}dx=(L/2)A_nδ_mn
A_n=-(2/L)(T₀-T₁)∫sin(½nx/L)dx
=-8(T₀-T₁)sin²(nπ/4)/(nπ)

So, finally,

T(x,t)=T₀-Σ{exp(-c²s_n²t)A_nsin(s_nx)}

c²=k/(C_pρ),
A_n=8(T₀-T₁)sin²(nπ/4)/(nπ)=4(T₀-T₁)/(nπ),
s_n=½nπ/L, n odd

We should tabulate the constants to be used:

T₀=100
T₁=10
k=226 W/m·K
C_p=900 J/kg·K
ρ=2710 kg/m³
L=20 m
c²=[k/(C_p·ρ)]=9.27x10^-5m²·

T(x,t)=100-Σ{(115/n)exp(-0.00206n²t)sin(nπx/40)} (t is in hours here.)

The plot of this function including just the first three terms of the series (1,3,5) is shown in the first figure. Note that because the bar is so long it takes the system several hundred hours to fully equilibrate. The second figure shows the calculation for the first hour; this is clearly wrong since the whole bar is at 10° at the beginning. The reason for this is that so few terms have been included in the infinite series. However, to understand the long-term behavior, n>1 plays almost no role because the n² behavior in the exponential damps out higher n contributions, particularly at large t.

One more calculation, for the initial temperature profile linearly decreasing over the length of the bar may be seen here.

QUESTION:
I'm writing a novel and want to make sure I'm describing a scene correctly. A spaceship built in a "tower" formation (rocket at the bottom, levels stacked on top of each other to the bridge at the top/front) is forced to land on Earth in an emergency. It initially enters at a steep angle nose first, causing rapid deceleration in the atmosphere, and then does a flip and burn, the engines faced to the ground and firing to slow them down. My question is around the gravitational forces an occupant would endure, sitting in a crash-couch/seat that cushions them and rotates to ensure they're always being pressed into it. Which way would these forces push/pull on them from start to finish, particularly around the flip and firing of the engine? I can't seem to wrap my head around it.

ANSWER:
Here is the trick you need to understand: Newton's laws, by which we usually do classical physics problems like what you are describing, are not valid in systems which are accelerating. When your astronaut is in empty space and turns on her engines, she thinks she feels a force pushing her into her chair; but she cannot understand this because she is at rest in her frame and Newton's first law says that if she is at rest all the forces on her should be zero. If we look at it from the outside we see the chair pushing her, that being the force which is accelerating her in accordance with Newton's second law. However, she can do Newtonian mechanics in her frame if she invents a force which is equal in magnitude to her mass times the acceleration of the system (rocket) but in the opposite direction as the acceleration; this is the "force" pushing her into the chair and in physics we call it a fictitious force. You have probably heard of a centrifugal force, the force which tries to throw you from a merry-go-round; that is a fictitious force because rotation is a kind of acceleration.

In the following examples, the green dotted line vector indicates the orientation of the chair desired for most comfort for the astronaut. Note that in each instance this vector points exactly opposite the net acceleration vector.

First the initial reentry, entering the atmosphere at a steep angle. The rocket has some velocity v. When it encounters the atmosphere the result is a retarding force opposite to the the direction of the velocity which causes an acceleration a of the rocket (and astronaut). There will also be an acceleration g due to the gravitational force (weight); if there were no air, this would be the only acceleration. The net acceleration is the sum of the two and is labeled a_net. The chair will orient with the green aligned with the net acceleration as shown.

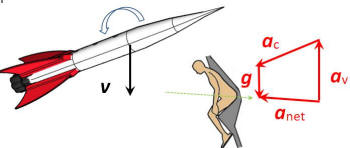Next we have the situation where the rocket is rotating to be tail down for landing. It is still falling with some velocity v so there is still an upward acceleration due to the air drag, labeled a_v here. There is still the acceleration due to gravity g. But now there is also a rotation about the center of mass of the rocket so there is a centripetal acceleration a_c experienced by the astronaut which points toward the axis of rotation. Add all three to get the net acceleration a_net. Now the chair will be aligned as shown.

Finally, the landing position which is the easiest. There is still the gravitational acceleration g. There is now an upward acceleration due to both the engines and the air drag but the engines will be the main contributer as the speed decreases. The net acceleration now points straight up and the chair orients as shown.

Keep in mind that I have not made any attempt to have any particular relative values of the various accelerations but they are not unreasonable. They will vary considerably depending on the specific conditions at any particular time.

QUESTION:
So from the movie space cowboys. Two pilots ejected from a plane and deployed their parachutes at different times. Assume they deployed their parachute at terminal velocity. They started at 100,000 feet. Assume same size parachute. If pilot A weighs 230lbs and deployed their chute 5 seconds later than pilot B who weighs 250lbs. How possible is it that pilot B gets to the ground first?

ANSWER:
Well, this is kinda tricky for a couple of reasons. First, "terminal velocity" is not some constant number; it depends on geometry of the object (which you try to keep the same by having "same size parachute"), the density of the air, and the mass of the object. So, falling from 100,000 ft they will experience very significant change in the density of the air. The second reason is that, because of the first reason, your phrase "deployed…at terminal velocity" doesn't really tell me much. Also, terminal velocity is not attained at a particular time so you would have to specify something like 'at 99% of terminal velocity'.

All that aside, let's do the calculation assuming that the density of the air is independent of altitude, the same as at sea level. The air drag is proportional to v² where v is the speed and I will call the proportionality constant k; k is where both the density of the air and the geometry of the falling object are 'hiding'. Then Newton's second law may be written as ma=mg-kv²where m is the mass, g is the acceleration of gravity, and a is the acceleration. Terminal velocity v_tis when a=0 or v_t=√(mg/k). Since we have stipulated that k is the same for both A and B and is altitude independent, only their masses would affect v_t. If they both jumped and never opened their parachutes, B would clearly be the winner (loser?!) since his terminal velocity is larger than A's as would be his speed at all times. Similarly, if each deployed his parachute immediately, B would get to the ground first. And, certainly, if A deploys first he will reach the ground after B since he was already behind and will end up falling more slowly than B. So, finally we come to your scenario where A deploys after B. What will happen depends on the altitudes where each deploy and how far ahead B is when A deploys. If A does not pass B during the 5 second free fall, B will get to ground first. If A does pass B he will end up below B but going more slowly; if they fall for a very long time B will pass A after some time. If that time is less than the fall time left for A to hit the ground, A will win.

Now, falling from 100,000 ft will be quite different because terminal velocities at very high altitude will be much greater than at atmospheric pressures. That means that the distanced between the two will be much greater when they have both deployed. If they wait until they are fairly close to the surface, it seems to me quite likely B will hit first.

QUESTION:
So, when earth moves faster around its axis (=one full rotation=1 day), does that mean we have a "faster time"? If time is correlated to biological age, does that mean we "age faster"?

ANSWER:
Time is not measured relative to any astronomical motions. If the earth were to spin twice as fast, that does not mean that time is running at twice the rate; rather it means that a day would now be 12 hours long. Any clock would run at the speed it did before the earth sped up. That includes biological clocks. (I have neglected relativistic effects which are exceedingly tiny at the speeds which the earth rotates.)

QUESTION:
In beta plus decay proton gets converted to neutron— where does the extra mass come from?

ANSWER:
A free proton does not (as far as we know) decay for the reason you have inferred from the masses; it must be inside a nucleus to β-decay. The nucleus begins with some mass M. It emits a β⁺, mass m_β and kinetic energy K_β; and a neutrino, mass m_ν and kinetic energy K_ν. The nucleus now has mass M' and kinetic energy K'. The energy of this isolated system must be conserved,

Mc²=(M'+m_β+m_ν)c²+K'+K_β+K_ν.

Essentially, the energy came from the mass of the nucleus; you would find the new nucleus more tightly bound than the original nucleus which you could interpret as being why it decayed in the first place. Therefore, β⁺-decay does not occur if the new nucleus is less tightly bound than the original. (By the way, the neutrino mass and kinetic energy of the nucleus are negligible in most cases.)

QUESTION:
Just listened to a Mark Parker Youtube where is was stated (obviously) that at the top of a sphere (the earth), say near the north pole, you are travelling slower, i guess in some reference frame, than someone at the equator. ie. you travel a shorter 'distance' in a a 24 hour period than someone at the equator (larger circumference, same 24 hr period). This is obvious with hindsight but not something I've ever tried to think about. My question is where does the additional energy come from if I travel south of the north pole (or north from the south pole) that enables me to travel faster (along the direction of rotation). I expect I'm misunderstanding the problem in some way. At the equator I travel 40000km in 24hrs or 1666.7km/hr (I'm assuming a spinning sphere and can ignore anything external to the earth). I've randomly picked a latitude of 60degrees where the circumference is 20000km, which in 24 hrs = 833.3 km/hr The degrees don't matter except to show a smaller circumference travelled in the same time (slower). So, as I travel north of the equator my rotational speed decreases. where does that energy go ? is the question valid. If I travel south of some arbitrary northern latitude towards the equator my rotational speed increases. Again, I'm grossly missing some key aspects of physics here. Am I actually (by travelling towards the equator) benefiting from the rotational energy of the earth, and when travelling away from the equator......actually is this a conservation of energy (or angular momentum) thing similar to pulling my arms in while spinning on a chair.

ANSWER:
You hit the nail on the head when you mentioned angular momentum conservation. You plus the earth are an "isolated system" with no external torques acting on you (forget the moon, etc.) and the angular momentum L of this system must remain constant regardless of how you move around. Suppose that you are at the north pole; then the angular momentum of the system is L₁=Iω₁ where I is the moment of the earth and ω₁ is its angular velocity. Now you walk down to the equator. The angular momentum is now L₂=(I+mR²⁾ω₂ where m is your mass and R is the radius of the earth. But, L₂= L₁ so if you do the algebra you will find that ω₂ =ω₁/(1+(mR²/I)). So the earth slows down by the tiniest amount; I estimate (ω₁-ω₂)/ω_₁≈10^-29=10^-27%! Regarding the energy, the initial energy is

E₁=½Iω₁²

and the final energy is

E₂=½(I+mR²)ω₂²=½Iω₁²/(1+(mR²/I))

and so

E₂/E₁=(1+(mR²/I))^-1.

So, the energy has not been conserved but is a tiny bit smaller even though your energy has increased by

½mR²ω₂²=½mv².

If you work it out you will find that the energy of the earth alone is

½Iω₁²/(1+(mR²/I))².

So we conclude that energy is lost by the system although you have gained energy, so the earth lost more energy than you gained. Energy is changed by forces doing work on the system, so what force is doing negative work here? Since we are in a rotating coordinate system, we will introduce the appropriate fictional forces so that Newton's laws can be used. If you are at some latitude θ, one force you will experience is the centrifugal force shown in the figure, C. It has two components, a normal component N which would reduce your apparent weight and a tangential component T which is trying to drag you toward the equator. In order to keep T from accelerating you, something must exert an equal but opposite force on you; this is simply the frictional force f between your feet and the ground. As you move toward the equator f does negative work thereby decreasing the energy of the system. Finally, the reason you gain energy is that there is another component to the frictional force which points also tangentially but perpendicular to f such that as you move south it speeds you up to keep the earth from sliding away from you.

QUESTION:
I'm trying to explain to my gf that if the car in front of us is moving 60mph we would have to be moving 60mph also in order to maintain a 25 ft distance behind it. I know it sounds dumb but I can't seem to make her believe it

ANSWER:
Ask her to imagine the car in front of you is going 60 mph and is towing you with a 25 ft rope. Ask her to imagine looking at your speedometer.

QUESTION:
This may be super simple but I keep wondering about it. If a vehicle in the void of outer space fires its boosters, why does it move anywhere? Here's why I ask: movement on Earth requires friction and a medium through which to move. If I'm in a swimming pool and kick off from the edge with my legs, then I move far. But if I'm in the middle of the pool and make the same kicking motion without contacting the edge, I probably won't move. Well, not unless I move a lot of the medium around me (the water). If there's no medium in outer space, why does the rocket booster have any effect? Here's my theory- is it correct? There's no resistance behind my spaceship, but there's no resistance in front of it either. After, say, the first second of the ship firing its boosters, the next second's worth of focused, exploding fuel is contacting the exhaust and energy of the first second. This gives the later seconds worth of exploding fuel something to push against and, with no resistance in front of the ship, it moves forward easily. Is this right?

ANSWER:
It is a common misconception that a rocket needs a "medium" against which to push, but it is wrong. Your attempt to think of a way to "create" an atmosphere to push against is therefore also incorrect. In order for something to accelerate, i.e. change its speed, all that is needed is for the sum of all forces on an object to be not zero. Even if you were on a surface with no friction and you were in a vacuum, you could start moving if someone behind you pushed you. The best way to understand a rocket is to consider the following example using the above situation of you in a vacuum with no friction on the floor.

You have a ball in your hand;
you throw the ball with some speed;
in order to give it that speed, you need to exert some force on it;
Newton's third law says that if you exert a force on the ball, the ball exerts an equal and opposite force on you;
therefore you end up moving in the opposite direction as the ball;
it turns out that the speed you acquire is smaller than the the ball's speed by the ratio of the ball's mass to your mass;
for example, if the ball has a mass of 1 kg and your mass is 100 kg, your speed will be 1/100 of the ball's speed.

The rocket engine is essentially throwing countless tiny "balls" (atoms, molecules, ions) with very high speeds to propel the rocket ship.

QUESTION:
If a system of two separate modules connected together with a linear passage(A spaceship carrying space traveler) is suspended in space with no gravitational influence and is rotating to create artificial gravity, at which point in the system will there be no force experienced by the accommodates while transitioning from one module to the other through the linear passage? It is the center I suppose, but I am unable to figure out the math.

ANSWER:
It depends on what the masses of the modules are. It also depends if the masses M₁ and M₂ of the modules themselves are much larger than the mass m of the person moving from one to the other. The pair will rotate about their center of mass which, if M₂=M₁, is at the halfway point. If the person is very light relative to the rest of the system, she will experience no centrifugal force at the center as you guessed; the reason is that the force is proportional the square of the speed she is traveling and her speed will be zero at the axis of rotation. But if m is not relatively small the location of the center of mass will vary when she moves from one module to the other.

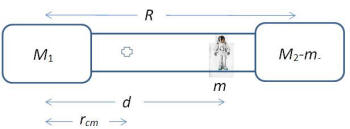
The following is probably more than you want, but I like to do it anyway. I will denote the masses of modules as M₂ and M₁, including anybody who is in them, and will treat them as point masses separated by a distance R; the traveling astronaut has mass m and is a distance d from M₁ and will also be treated as a point mass and I will assume the passage has negligible mass. The center of mass is located a distance r_cm from M₁. Calculating the center of mass location relative to M₁ is straightforward and results in

r_cm=Σ(m_ir_i)/Σ(m_i)=[(M₂-m)R+md]/(M₂+M₁)

For example, if M₂=M₁=M,

r_cm=½R-(m/M)(R-d);

and if m<<M,

r_cm≈½R.

Now, you are interested in when d=r_cm:

d=R(M₂-m)/(M₂+M₁-m).

And again, for a check, if M₂=M₁=M,

d=R(M-m)/(2M-m),

which is, if m<<M,

d≈½R.

QUESTION:
Okay so lets say your free falling from some odd feet in the sky in a car. Dont worry about the reason why but that its happening. If you put yourself in a position to jump out of the car before it hits the ground and explodes, will you be able to change your momentum enough to not take so much damage from hitting the ground so fast?

ANSWER:
It depends on how far the car has fallen. If it falls from say 10 ft, you could do it fine but wouldn't even need to jump. But if the car fell from a high enough altitude to reach its terminal velocity, which I estimate to be about 200 mph, could you survive it by jumping upwards at the last minute? How high can you jump from the ground? The highest humans can jump is about 6 feet and to do that requires that you can jump up with a speed of about 13 mph. If you jumped that fast relative to the falling car, your speed relative to the gound would be about 187 mph; you would be just as dead as you would have been if you hadn't bothered to jump.

QUESTION:
Hello. If a 200 pound man runs at 5 miles per hour, hits another man going same speed same weight, opposite. What is the force of impact? Fyi. I'm 56. Past homework!

ANSWER:
There is no way to answer this question because it depends on the details of the collision. What matters most is the time the collision lasts (or, equivalently, the distance over which each moves during the collision) and whether the two essentially stop or each rebounds backward. I can give you a couple of suggestions. I will work in SI units (v=5 mph=2.25 m/s, m=200 lb=90.7 kg) which is usual for physicists and will convert back to imperial units (pounds) at the end. I will assume that the collision is perfectly inelastic, that is both runners are at rest following the collision; in that case all the kinetic energy the two had (each has ½mv²=230 J) is lost in the collision.

Suppose, first that the two have lowered their heads much like bighorn sheep do when fighting. Since there is not much flesh on the forehead, they will stop in a very short distance, let's say d=5 mm=0.2 inches. The work done by the average force each man feels must equal the energy he lost, Fd/2=230 J so F=460/0.005=92,000 N=20,700 lb; of course, this force will be spread out over an area of several square centemeters. Still it is pretty darned big.

Suppose the two men have big beer bellies and that is where they collide. Then the distance over which the collision occurs will be more like 5 cm and the resulting force more like 2000 lb. And, the force will be spread over a much larger area.

In the real world, such a collision would occur over a large amount of the body so the total energy, converted as a force, would be spread out over maybe a square meter. places which are hard (like your head) would be hurt more badly than places which are softer (like your torso). Also, if the forces look unbelievably big, keep in mind that they last for a very short time.

QUESTION:
If energy and mass are interchangeable or equivalent can E=mc² be written as M=ec² and mean the same thing? Thanks! I'm totally ignorant maybe there's is an obvious reason why not here.

ANSWER:
Mass and energy are not "interchangeable or equivalent". That would be like saying that electricity and wind, both forms of energy, are the same thing. Mass is a form of energy and the total amount of energy which a mass potentially has if it could be totally converted into energy is given by E=mc². If you wanted to know how much mass could be realized by converting an amount of energy into mass, m=E/c². Another way to see why your M=ec²is an impossible equation is by doing dimensional analysis: The units of mc² must be kg·m²/s² so energy must have units of kg·m²/s²; but your equation would have the units of energy being kg·m⁴/s⁴ which is not what the units of energy are.

QUESTION:
I hope there really is no such thing as a stupid question, if there is you are really in for a treat. Okay, so if something is being propelled from the rear it is being pushed, and if something is being propelled from the front it is being pulled, correct? Is there a term for something being propelled from the front AND the rear at the same time?

ANSWER:
The words 'push' and 'pull' are qualitative words, not physics words. Pushes and pulls are both denoted a forces in physics. For example, if you have a horse pulling on a cart with a force of 100 lb and a man pushing on the back of the cart with a force of 10 lb, the net force on the cart due to these two forces is 110 lb forward. If the man is instead pulling on the back of the cart, the net force is 90 lb forward.

QUESTION:
Light cannot escape a black hole. What is the nature of light inside a black hole, theoretically? Static photons? Can light be "static" and exist in only one point in space time? Perhaps it ricochets around inside the event horizon rather than static? Perhaps gets squeezed into a different subatomic particle? Am an old guy who has to much time and thinks of such things.

ANSWER:
Note that I usually do not answer questions on astronomy/astrophysics/cosmology as I state on my site. When light is captured by a black hole, it ceases to exist as photons and basically becomes mass, increasing the overall mass of the black hole. When you when you ask what is going on "inside a black hole" it can mean two things: either inside the Schwartzchild radius (from inside of which no light can escape) or inside the black hole itself. There is no answer for the latter because at nearly infinite density we have no idea at all as to what the laws of physics are. For the former, you can say that a photon loses energy as it falls from the Schwartzchild radius to the surface of the black hole, the lost energy being converted to mass; the photon continues moving at the speed of light but its frequency decreases until the photon disappears at the surface of the black hole, totally converted to mass.

QUESTION:
Say you have a rocket ship in a vacuum away from all gravitational fields firing its engines to maintain uniform circular motion. Since the engines are burning fuel, it makes sense to me to calculate the power output in watts. But the Force in the direction of the Velocity is zero so the power is zero. I'm confused. And since the Kinetic energy is not increasing, where does the energy expended by the engine go?

ANSWER:
You are going to have a rocket engine which can fire perpendicular to your velocity vector. None of the energy generated by the engine will be given to the rocket ship because the force the engine applies is perpendicular to the displacement, hence no work is done. The energy generated goes into the kinetic energy of the ejected gases. It will be a little tricky to maintain uniform circular motion because mass is being ejected, so as the ship loses mass you need to reduce the force to keep velocity and radius constant: F=mv²/R.

QUESTION:
How can universal gravitation and conservation of energy both exist together? If gravitation is universal there should be no where in the universe where a system is not acted on by an outside force (gravity).

ANSWER:
Conservation of energy is applicable to systems with no external forces doing work on them. You have to be very exact when applying conservation principles. Suppose you choose the solar system as the system; if the solar system were in the middle of empty space its energy would be conserved, but it isn't an isolated system in real life and the rest of the galaxy exerts forces on it which might change its energy. Suppose you choose the milky way galaxy as the system; if the galaxy were in the middle of empty space its energy would be conserved, but it isn't an isolated system in real life and the Andromeda galaxy, the nearest major thing which exerts forces on it, would change its energy. You can see where I am going with this. Suppose the entire universe were the system; then there are only internal forces acting on this system so its energy will not change.

QUESTION:
I have some understanding issues with Current and Voltage regarding Induction. When there is a change in magnetic flux there must be either a change in the area of the e.g. wire or the magnetic field. But how is there a flow of current then induced by it without any poles where I can measure the voltage. I guess, it's just me thinking wrong of voltage, but I really didn't understand that one if you ask me. Connecting to that, how must I think of a coil that is getting an induced voltage by changing magnetic flux. How are the electrons flowing through the coil, because right now i always try to think, that in every nth part of that coil there is some sort of electric field that is created because of the electrons getting pushed. I really do think it's a question of understanding, but the mathematic definition and explainition is not really enough for me, i want it visualized for me.

ANSWER:
When electricity and magnetism is taught, there is usually a sequence:

First we talk about electrostatics where all electric fields are constant and conservative. A conservative field is one for which, if you move an electric charge from one point in the field to another, the amount of work you do is independent of the path you choose. This means that potential difference (voltage) between two points is a meaningful number. You are worried because you have been told that a wire loop with no battery in it might have a current cannot flowing in it.
Next we talk about magnetic fields which are caused by electric currents which are constant and presumably caused by potential differences. This is called magnetostatics.
Finally we come to the full theory of electromagnetism where the fields are no longer constrained to be constant.

All of electromagnetism is described by Maxwell's four equations. It gets mathematically dense so I have previously qualitatively described these equations without any math.

Electric charges cause electric fields.
Electric currents cause magnetic fields.
Changing electric fields cause magnetic fields.
Changing magnetic fields cause electric fields.

So the answer to your question is that you do not need charges to create the electric field which will drive a current; a loop of wire will have a current running in it if you cause the magnetic field passing through its area to change. This is called Faraday's Law.

QUESTION:
Okay, so i may dissagree with a master here, aka. Stephen Hawkings himself, but i have some questions that need to be answered, so here goes. Hawking Radiation. It's basically a theory that says particles and anti-particles spontaneously materialize in space, seperating, joining, and annihilating each other. But then a black hole comes and sucks the a particle, leaving the other without a partner to annihilate with. This particle appears to be in the form of black hole radiation. Sooo, blackholes are not eternal. But what if all of the particles are sucked into the black hole? This is particle and anti-particle that we're speaking of, that has POSITIVE mass. It's not exotic particles that have NEGATIVE mass right? So does Mr. Hawkings law apply? Please answer this, i'ts kinda been bugging me for a while...

ANSWER:
First I will note that I do not normally do astronomy/astrophysics/cosmology, as clearly stated on the site. However, since I have answered this and related questions many times before, I will accept your question. I would say that you stop thinking about mass and simply think of energy. A particle can have negative energy without having negative mass. I think the best and most detailed answer I have given is here.

QUESTION:
why light cannot curve around object

ANSWER:
In fact, light does curve around an object with mass. Originally it was known that light had no mass and therefore would not be affected by gravity. But Einstein's theory of general relativity predicts that light passing near a massive object like a star or a galaxy will be deflected. This has been observed to be correct. There is a nice article on gravitational lensing on Wikepedia. However, for everyday life the bending is hardly noticeable because it is small. Even the entire earth has too little mass for this bending to be noticable (see a recent answer).

QUESTION:
Assuming no prior information is given, except the formula for the time period of a pendulum (T=2π√(L/g)), would the time period of a swing be changed at all if someone went from sitting down on the swing to standing up on the swing? Eg. would the mass distribution affect the time period?

ANSWER:
The formula you state is true only for a point mass M attached to a massless string of length L. Therefore you cannot solve this problem using that formula. However, you could guess that the period would be proportional to the square root of the distance D from the suspension point to the center of gravity of all the mass (the person, the swing, the ropes). In that case, the period would get smaller when the person stood up because the center of gravity would be closer to the suspension point. The correct equation for the period is T=2π√[I/(MgD)] where I is the moment of inertia about the suspension point.

QUESTION:
Under "miscellaneous" here on your site, you answer the following question: "If the earth is curved how is it you can get a laser to hit a target at same height at sea level more then 8 km away? How is it that it's bent around the earth?" Part of your answer states that the laser is perfectly straight. But spacetime is bent (curves) within the gravity well of a massive object like the earth. Astronomers have shown that it's possible to see stars that are actually behind such massive objects because the light from the star is bent around the massive object as it necessarily follows (somewhat) the curvature of spacetime around the object. So how is the laser beam in the question you answered perfectly straight?

ANSWER:
It was clear to me when I was answering this question that the questioner was interested in a classical physics question, not one taking general relativity into account. You are right, any mass (or other energy density) will cause a ray of light to bend. But in this case the amount of bending is very, very tiny. If you apply the angle of deflection equation θ=4GM/(rc² to a beam of light tangent to the surface of the earth at the surface of the earth, you will find that θ≈0.0006"=1.67x10^-7°. I think you will agree that this is negligible in the context of the question I answered!

QUESTION:
It takes 375 joules of energy to break a human bone. How high must a 60kg person fall to break a bone?

ANSWER:
There is no answer to this question. And it really does not make any sense because it is force, not energy, which breaks a bone. If you delivered 0.01 J/s over 37,500 s (approximately 10 hours) would you break the bone? So what matters is the time the stopping collision takes to deliver the energy impulse.

QUESTION:
Why doesn't your brain explode in a PET scan? Doesn't antimatter meeting matter create a lot of energy?

ANSWER:
Yes, matter/antimatter annihilation releases the maximum amount of energy—when a positron meets an electron, 100% of their mass is converted into energy. But how much mass do they have and how much energy is that? Each particle has a mass of about m=10^-30 kg, so their total mass is about 2x10^-30 kg. The energy is then E=mc²=2x10^-30x(3x10⁸)²=1.8x10^-13 J where c=3x10⁸ m/s is the speed of light. To put this into perspective, this would be the energy of a particle of dust which has a speed of about 2 inches per second. Furthermore, nearly all of the energy (which is in the form of two x-rays) escapes without leaving any energy in the brain.

QUESTION:
Hi, hoping you can help settle a debate I'm having with a colleague. We know that when a solid object spins, radial and circumferential tension exists within it due to centripetal/centrifugal force. However, for a massive object such as a planet, whose gravitational acceleration far exceeds centrifugal force, does that tension still exist within the object? I say that the product of gravitational and centrifugal forces results in a net force towards the object's centre of mass leading to a net compression, and an object under compression cannot also be under tension. He states that the tension that would have existed due to the centrifugal force only would still exist and that the gravitational force makes no difference to this. As you can probably tell we're not physicists! Can you help answer whether tension (such as a hoop stress force) would still exist in such a massive object, or would the gravitational force 'overwhelming' centrifugal force prevent tension from forming in the first place?

ANSWER:
Whenever you want to understand something, you need to include all the forces acting on it. Centrifugal force is what we call a fictitious force, it doesn't really exist. When you are experiencing an acceleration, Newton's laws do not work. However, if you add fictitious forces cleverly, you can do Newtonian physics. If we are in a rotating system like the earth we are accelerating because in physics acceleration does not just mean speeding up or slowing down but also includes changes in your direction which is constantly happening to you as the earth spins (unless you are at a pole). To see how this works, look at an earlier answer. So, suppose that you are standing on the equator; there are three forces acting on you, your own weight (gravity) which points toward the center of the earth, the centrifugal force which points away from the center of the earth, and the force (which points up) which whatever you are standing on exerts to keep you at rest. Suppose that your mass is 100 kg and the acceleration due to gravity is approximately 10 m/s²; then your weight is approximately 1000 N. The centrifugal force is your mass times your speed (464 m/s) squared divided by the radius of the earth (6.4x10⁶ m), C=100x(464²)/(6.4x10⁶)=3.4 N. Suppose you are standing on a scale; since you are at rest, the force which the scale exerts up on you is 1000-3.4=996.6 N, about 0.3% smaller than your weight. This is a long-winded answer to your question: yes, forces due to rotation apply to anything regardless of its mass or size. (If you are not comfortable with metric units, 1000 N=225 lb and 3.4 N=0.76 lb. If you weighed yourself at the poles the scale would read 1000 N if the earth were a perfect sphere.

Here is another example: the earth is not a perfect sphere, it bulges at the equator. The reason is that the earth, when it was just forming billions of years ago, was very hot, almost molten, and therefore more "plastic"; so the centrifugal force caused it to flatten as it rotated. That would mean that your weight at the poles would really be greater than what it is at the equator because it is closer to the center of the earth.

QUESTION:
Hey, i wanted to discuss about the MPEMBA EFFECT. Mostly i have read that it has no valid and accepted explanation but i think it should be taken as common sense like if we draw an analogy with electrodynamics we can say that a body with higher temperature should be at higher potential and a cold body should be at lower temperature. So as the potential difference gets bigger the rate of flow of charge(current) gets higher, similarly the rate of flow of heat charge should also get higher. Hence, it should be taken as obvious that a hot body will cool down much faster than a relatively cold body.

ANSWER:
I first note that I have already given a quite lengthy answer to the "hot-water-freezes-faster" hypothesis. As you will see, what happens depends a lot on the conditions of any measurement or experiment you might try to do. Your attempt to bring in "potential" is pretty muddled, so let's review rate of flow in electrodynamics and in thermodynamics. Materials have a property called electrical conductivity; this property tells you how much electric current you will get if there is a voltage (potential difference) between two points in the material—the larger the conductivity, the larger the current will be. Similarly materials have a property called thermal conductivity; this property tells you the rate at which heat travels throught the material for a given temperature difference—the larger the temperature difference, the larger the energy flow will be. But, this will have very little influence on how quickly the water will freeze. First, the change in thermal conductivity of water changes by only about 10% between say 20°C and 70°C; second, water is not a very good thermal conductor; and third conduction is not the primary way water cools because the density of water, unlike most materials in the molten state, gets larger as it cools, the cooled water at the surface sinks so most of the transfer of heat inside the water is by convection. Certainly the hot water loses energy at the surface faster than the cold water, but it will eventually catch up with the cold water and then the two will be indistinguishable unless the cold water freezes before the hot water catches up with it. As I explained in the earlier answer, evaporation cools the hot water more and if a significant amount of the hot water evaporates before it catches up to the cold water, it will win the race because there is less of it; but that is really cheating, isn't it. Sorry, I do not know anything about the mpemba effect.

QUESTION:
I just want to ask if, can we solve the force of attraction between two identical pendulum bobs with only mass(0.35kg) as given? Is it solvable? I am just curious about this, my teacher discussed about this topic but with enough components to solve it. But with this problem, I really can't think of something to solve it with only one given component.

ANSWER:
You cannot calculate the gravitational force without knowing the distance between them. And you could not easily calculate the force unless the bobs were spheres.

QUESTION:
I was wondering, in particle annihilation between say a electron and a positron, how long does it take to occur? I know it's refered to as being instantaneous, or happening in a immeasurable amount of time in clearer terms.

ANSWER:
I believe there is no good answer to this question because when would you start and stop the clock? And even if you could specify some particular times, they would inevitably depend sensitively on the initial conditions like how fast each was moving initially. You can, however, measure the lifetime of a positronium atom (one electron bound to one positron). In vacuum the singlet state (spin zero) atom has a lifetime of about 0.125 ns and the triplet state (spin one) has a lifetime greater than 0.5 ns. The times for the atom in various materials would be longer.

QUESTION:
If a carousel is out of control, spinning at high speed, and suddenly it is stopped, there will be chaos and horses and riders flying out of the carousel structure. How do you explain this in terms of physics? Are they ejected due to the centrifugal force? Loss of centripetal force? And what happens to the kinetic energy? Is it transformed to what kind of energy?

ANSWER:
If the carousel is moving in a circle with constant angular velocity, the only forces horizontally are forces necessary to provide the centripetal acceleration. In the photo, the girl holds the pole and presses on the side of the horse with her leg to provide those forces; the horse is held by the force of the pole to which it is attached. All horizontal forces are toward the center of the carousel because the speed of everything on the carousel is constant. What happens if the carousel suddenly stop. All those radial forces quickly drop to zero. The tendency is for everything on the carousel to continue moving with the velocity they had before, but now in a straight line. But now, although the horizontal radial forces are gone, each object experiences horizontal forces opposite the direction of their velocities. The girl would initially move forward until she smashed into the pole; the horse would probably be held in place by the pole although the force required to stop the horse could very possibly bend the pole; someone standing on the spinning floor would only have the friction of the floor to stop her and would likely keep moving in a tangential direction. Nothing is "ejected", it just keeps going in the direction it was going when the carousel stops, unless something stops it.

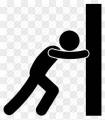
QUESTION:
I push on a wall and am accelerated backward. Per Newton's third law, how does the acceleration of the wall manifest itself.

ANSWER:
You push on the wall with some force F and, as you note, Newton's third law says that the wall pushes with a force -F. So the magnitude of your acceleration a is a=F/m where m is your mass. The magnitude of the wall's acceleration A is A=F/M where M is the mass of the wall. For all intents and purposes, the mass of the wall is infinite so its acceleration is zero.

QUESTION:
Are electrons made of quark/anti-quark pairs? If yes, which pair?

ANSWER:
No. To the best of our knowledge electrons are elementary, i.e. they have no components.

QUESTION:
What force pulls the train? I am doing a science project about this simple electromagnetic train. This project looks so simple yet so complicated, here is the video of the project that I am working on.

ANSWER:
The construction details and a brief description of the physics are shown in another youtube video. Essentially, when the magnets touch the copper wire the battery causes a current to flow in the coil between the two batteries which causes a magnetic field in that section of the coil; each magnet, now being in that field, experiences a force moving it forward. Important things:

The same pole, north or south, must point away from the battery.

Be sure to use bare copper wire. Often copper wire has an insulating layer on its surface and this would not allow current to flow

Good luck on your project. It is really not as complicated as you thought.

QUESTION:
I can't grasp how two waves can pass each other on the same piece of string. For a wave to travel on a string each piece of string is, let's say, pulled up wards by the preceding piece of the string, and the wave propagates forwards. If a wave moving in the +x direction meets a reflected inverted wave in the - x direction, a node will be formed as one wave pulls that piece upwards and the other wave pulls it downwards. Therefore the piece of string doesn't move, so how can either wave travel past this point?

ANSWER:
What you need to understand to see why the two waves, moving in opposite directions are able to do so is a little bit of the physics of waves on a string. Any wave which moves through a medium is a solution of a very famous equation, the wave equation:

d²f(x,t)/dt²=v²d²f(x,t)/dx².

Here, x the position on the string, t is time, v is the velocity of the wave, and f(x,t) is the solution to the equation which will describe the shape of the wave at a time t. You may not know calculus and this equation is goobledy-gook to you, but all you need to know is that, mathematically, any function f is a solution as long as it of the form f(x-vt). The most commonly used example of waves is sinesoidal, for example, f=Asin(kx-ωt) where k is called the wave number and ω is the angular frequency of the wave. Note that ω/k=v. Also, to touch base with quantities you might be more familiar with, k=2π/λ and ω=2πf where f is the frequency of the wave and λ is the wavelength. Now comes the the important part: because any f will be a solution to the wave equation, if you have a wave traveling to the right, f_right=Asin(kx-ωt), and an identical shaped wave traveling to the left, f_left=Asin(kx+ωt), their sum will also be a solution to the wave equation. As you can see from the figure, waves traveling simultaneously right (red) and left (green) add up to a "standing wave" (brown) which does not appear to move but is still oscillating*. You are correct, there are nodes which do not move but both component waves go right on by them nevertheless, it just isn't apparent when you look at there sum. The fact that the net motion of the medium (string) is just the sum of all individual waves is called the superposition principle.

*If you're handy with trigonometry, you can calculate f_right+f_left which is apparently not moving even though you know that before you did the calculation you could certainly see that it was two waves.

QUESTION:
Hi, I have been toying with the concept of using gravity as a perpetual energy source, and have had a lot of pushback in the process of trying to ask questions. The conversation usually ends before I can get an answer. The skepticism surrounding perpetual motion is understandable. If I understand correctly the issue is that closed systems lose energy to various forces such as friction. Firstly, does it count as perpetual motion if the energy is supplied constantly from outside forces?Secondly, if not, is there a proper term for what I've described?

ANSWER:
I am afraid that you have it exactly backwards. In a closed system, defined as one which has no external forces acting on it, energy is conserved. In a closed system where friction is present, when kinetic energy is lost (e.g. a spinning wheel slowing down or a box sliding to a stop on a surface), the lost kinetic energy shows up mainly as heat. And, if you do work on a closed system to keep it moving forever, that is not what we mean by perpetual motion. Proper term for what? If you mean motion that you keep going by pushing on it, it has no particular name.

QUESTION:
First, I am way out of my field of understanding here so please keep it simple. I watched some videos on E=MC2 which led to how light reacts differently than matter at high speeds causing time to slow down when moving fast. My question is, if I was to shine a flashlight perpendicular (90 degrees) to the direction traveled am I correct to say if I was mo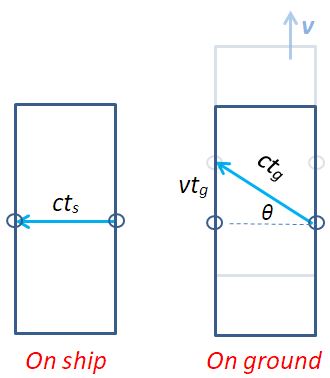ving at half the speed of light the beam would actually be at a 45 degree angle and when travelling at the speed of light the beam would be horizontal (0 degrees). This would also be true whether the beam was inside or outside of the spacecraft, correct?

ANSWER:
No, you have it wrong. The most important thing to remember here is that the speed of light, c, is the same for all observers. If you are in the rocket and shoot a beam of light straight across the ship, it will go straight across the ship in some time t_s and the distance it goes will be ct_s; if the width of the ship is w, t_s=w/c. Now, someone on the ground will see the rocket moving by with some speed v, so the point on the inside of the ship where the light beam will have moved a distance vt_g when the light strikes it; but since this is light, the distance it will travel is longer because the light has to go farther. Now, to find the angle the light relative to the perpendicular to the velocity v, we note that sinθ=v/c (t_g cancels out). In your question, since v=c/2, so θ=sin^-1(0.5)=30°. This example also demonstrates time dilation because the two observers see different times of transit of the light. If you work it out, t_g=t_s/√[1-(v²/c²)].

QUESTION:
The radius of earth is 6440 km . Suppose, the angle between Canada and USA inside the earth is 10 degrees , then what is the distance between them? I have been stuck with this problem . Can't i answer this problem using The Cosines Laws? If i do so....does it would go wrong? please answer my question...? It is not a homework question . i am thinking to solve this one with a different way....

ANSWER:
This is a very strange question because the USA and Canada are adjacent and therefore the angle would be 0°. However, you can easily find the distance between two points which subtend 10° just by knowing the definition of radian measure of angles. The angle θ subtends a distance s for a circle of radius r. This angle, in radians, is defined as θ=s/r. Since the circumference of a circle is 2πr and there are 360° in a circle, there are 2π radians in 360°. So 10°=10x(2π/360)=0.175=s/6440, so s=1124 km.

QUESTION:
Hi! I would like to settle a bet with my father. My questions is that if I was sitting in a chair that was tied to a rope, and the rope was divided by a pulley on the ceiling, would it be possible to lift yourself up just by pulling down on the other side of the rope.

ANSWER:
The figure on the left shows all the forces on you: T is the force which the rope exerts up on you*, N is the force which the seat of the chair exerts up on you, and Mg is the force of gravity (your weight) down on you. Choosing +y up as indicated, Newton's second law in the y direction is, for you, N+T-Mg=Ma where a is your acceleration and M is your mass. The figure on the right shows the forces on the chair: -N is the force you exert on the chair, the same magnitude but opposite direction as the force the chair exerts up on you because of Newton's third law; T is the force which the rope exerts up on the chair, the same magnitude as the tension on you because the rope and pulley are assumed to have negligible mass; mg is the force of gravity (weight) down on the chair. Newton's second law in the y direction is, for the chair, -N+T-mg=ma where a is the acceleration of the chair (the same as yours) and m is the mass of the chair.

Let's first assume you are exerting just the right force T on the rope so that you are at rest, so a=0. In that case, if you solve the two equations you will find that T=(M+m)g/2. In other words, you need to be able to exert a force down on the rope which is equal to half the weight of you and the chair combined to hold the chair from falling. All you need to do is be able to pull just a little harder to move upwards. That answers your question but it interests me to look at a case where a is not zero.

If you solve the two equations for a and N you get

a=[(2T/(M+m))-g] and

N=T(M-m)/(M+m).

A few observations about what these results tell us:

If you let go of the rope, T=0, a=-g, N=0; you and the chair are in free fall.
If m=M, N=0, a=(T/m)-g; the motion of you and the chair are identical even though there is no interaction between you and the chair.
You will accelerate upwards if T>½(M+m)g, half the total weight. Your strength is the only thing limiting how fast you can accelerate upwards.
If 0<T<½(M+m)g you will accelerate downward with an acceleration smaller in magnitude than g. Of course T<0 is not possible for a rope.

*It is important to note that, because of Newton's third law, if the rope exerts a force up on you, you exert an equal and opposite down on the rope. T is a measure of how hard you are pulling. How large T can be depends only on how strong you are and how strong the rope is.

QUESTION:
We define image as the intersection point of reflected rays and the focal point is the point at which light will meet after reflection. So, why is it that we have different positions of image when object is placed at different distances from concave mirror and not always at focal point except when object is placed at infinity?

ANSWER:
Because only rays which come in parallel to the optic axis are reflected through the focal point. This occurs only (approximately) for objects very far from the mirror.

QUESTION:
Does radiation from your phone stay on your hands after you use it?

ANSWER:
Absolutely not. Any radiation from the phone is electromagnetic, essentially radio waves. It is transient and does not "stay" anywhere. Even when you hold the phone the radiation is not "on your hands" but harmlessly passing through them just like the waves from some radio station is passing through your whole body.

QUESTION:
When a uranium or plutonium atom is fissioned, energy is released visa E=MC2. I believe this energy is in the form of photons. What I do not understand is how these photons (light) create such high temperatures in an uncontrolled nuclear explosion. Can you please explain?

ANSWER:
Actually, emitted photons account for only about 2.5% of the total fission energy. Emitted neutrons account for 3.5%. Most of the energy is contained in the kinetic enerngy of the fission fragments, 85%. The other approximately 9% of the total energy shows up later when the fission fragments, which are not stable, decay radioactively, mainly from β-decay. The high temperatures are due to the kinetic energy of the fission products which have speeds typically 3% the speed of light.

QUESTION:
I'm embarking on a horological project. I need to buy a very particular type of spiral spring. I guess it's a type of torsion spring. The only supplier I can find who sells these springs classifies them with two numbers. The overall diameter in mm and the torque in gm/cm/100°. (As noted below, I assume that this means the torque on the spring when the angle is 100° and it should be gm·cm, not gm/cm.) I know the spring I need. But I only know in terms of the CGS System. I'm following an old book and I've ascertained that the spring I need has a "CGS number" of 0.76. So, my challenge is to find a way to convert between these two unfamiliar units of torque measurement. A "CGS number" and gm/cm/angle. There are plenty of calculators for converting between different units of torque. But I don't think it's as simple as that. I have two questions. I know a bit about the CGS system and there is loads of info online. But I'm not clear what it is in the context of classifying a torsion spring. The book only says "the CGS number indicates the restoring couple of the spring when its diameter is 1cm." So what is the CGS number exactly? Is it dyne-centimetres? If so, then that's easy to work with since that's a measure of torque I'm familiar with. So I'm half way there. If it's something else, then perhaps you can help explain. Then there is the question of gm/cm/angle. The problem is that none of the calculators I've seen have a notion of angle. This is specific to torsion springs. The torque, in this case, is the working load when the spring bends 100°. Will I ever find the correct spring? Sadly, I have spoken to the manufacturer, and they were unable to help me.

ANSWER:
I think the "number" of interest is not a torque, rather the spring constant associated with the spring for angular displacement. First, a review of linear springs which when stretched stretch a distance x when a force F is applied to the spring. It is experimentally determined that, to an excellent approximation for a good steel spring, is that the distance stretched is proportional to the force applied, x∝F or F=kx. The proportionality constant k is called the spring constant and is measured, in SI units, as N/m (Newtons per meter) [dynes/cm in CGS units, lb/ft in Imperial units]. k indicates the stiffness of the spring and this equation is called Hooke's law. The form of Hooke's law for angular motion (as in a torsion spring) is that the angular displacement θ is proportional to the applied torque τ or τ=κθ; I believe the quantity you want is κ (kappa) and is measured, in SI units, N·m/radian [dynes·cm/radian in CGS units, lb·ft/degree in Imperial units]*. I have noted that κ is often called, by manufacturers and vendors, the rate of the spring since it is the rate of change of torque per unit angle. I am puzzled by your reference to a constant defined as gm/cm/degree; 1 dyne=1 gm·cm/s², so κ should have units gm·cm²/s²/degree; sometimes the gram is treated as a unit of force (called a gram force where 1 gram force=980 dynes), in which case κ would be gm·cm/degree, not gm/cm/degree. So, there must be somewhere in the reference you are using a definition of what the CGS number is. Suppose that it is 0.76 dynes·cm/radian (which would be the likeliest units if purely CGS system of units is applied) but you want it in lb·in/degree; then 0.76 (dyne·cm/radian)x(2.25x10^-6 lb/dyne)x(0.394 in/cm)/(57.3 deg/radian)=1.18x10^-8 lb·in/degree. Or, suppose you wanted it in (gm force·cm/degree); then 0.76 (dyne·cm/radian)x(gram force/980 dyne)/(57.3 deg/radian)=1.39x10^-5 (gm force·cm)/degree).There are lots of unit converters around, my favorite is here.

The choice of units for κ which it seems most vendors use is lb·in/deg. The best calculator I found to get an idea of the magnitude of these springs can be found here. Until you are able to deduce the units of the so-called CGS value of 0.76 you cannot know what it is.

*Sometimes κ is implicitly given by specifying the torque at a particular angle.

ADDED THOUGHTS:
In the book by Hans Jendritzki, Watch Adjustment, he says that in the CGS system for characterizing the spring in question (which I will call N_CGS), the unit of force is the dyne and the diameter of the spring is 1 cm. He then uses not the restoring torque to calculate N_CGS but rather the restoring couple associated with the force; the restoring couple is the restoring force times the diameter whereas the torque is the restoring force times the radius. Most vendors use the restoring torque to characterize springs, so ½N_CGSshould be used to convert to the vendor's units. Although the units of the angle are not given in Jendritkzi, I have found that the more natural radians gives values much too small when converting to vendor units; so N_CGS=(restoring couple in dyne·cm for 1 cm diameter)/degree. One vendor charactorizes the spring by specifying a torque given by N gm/cm/100°; this does not appear to be dimensionally correct unless the gram is gram force (I will denote it as gmf) where 1 gmf=981 dynes (the weight of 1 gm in dynes) and /cm means that again this is for a 1 cm diameter spring. So, assuming that the vendor's torque is indeed torque (force times half the diameter), ½N_CGS=N. For example, suppose N_CGS=2; then N=½(2) (dyne·cm/1°)(1 gmf·cm/981 dyne·cm)/(100°/1°)=0.102 gmf·cm/100°; so the conversion from the CGS value to this vendor's value is N=0.0491N_CGS. So, in the case of N_CGS=0.76 dyne·cm/1°, N=0.037 gmf·cm/100°.

[Disclaimer: I am not a clockmaker and I am not familiar with conventions clockmakers might use or meanings they may attach to certain words which are not in accordance with definitions, units, or conventions used by physicists. In the event that I have misunderstood or that either Jendritkzi really meant torque or the vendor really meant couple, the conversion factor would be 0.102 instead. I have done my best to determine conversions between two numbers representing the same thing but in different systems of units.]

QUESTION:
If you lined up frictionless gears over an exceptionally long distance, could you effectively communicate faster than the speed of light through one person moving the first gear and a second person reading/interpreting the resulting movement of the last gear?

ANSWER:
I have answered this question in many guises many times. In your variation, each gear will experience a force from the previous gear in the line and exert a force on the next gear. The time it takes for the force to travel from the input force location to the output force location is determined by the speed of sound in the gear. The message you send would travel at the speed of sound, much smaller than the speed of light.

QUESTION:
If you are driving side by side at 60mph with another car and throw a can of coke at them would the can be travelling at the same speed so hit the target as if you were parked next to each other or merely disappear behind your vehicle?

ANSWER:
When you throw it out the window it originally has a forward component of its velocity of 60 mph. At this speed, the can will experience a very significant force slowing its forward velocity down because of the air drag. So the can will not keep pace with the two cars and will appear, from either car, to be accelerating backwards. So, no, the can will not hit the other car where it would have if the cars had not been moving.

QUESTION:
Under relative motion, it's experimented that A person sitting on a back seat in a moving bus has a speed with respect to the earth which is the same as that of the bus. But if he now walks towards the driver of the bus,he has a speed relative to the earth which is more than that of the bus. Suppose the bus is moving at 100km/h and the person walks at 5km/h towards the driver, his forward speed relative to the earth is 100+5= 105km/hr. But when he walks back from the driver to his back seat at the speed of 5km/hr his speed relative to the earth is now 100-5= 95km/hr. WHY the increase speed of such person when moved forward and the decrease when moved backward

ANSWER:
The problem you are having is that you do not understand the phrase "relative to the earth". Let's alter your example by having the train moving at 5 km/hr. If you are in the train walking 5 km/hr in the opposite direction, someone standing by the side of the tracks will see you standing still; the same as running on a treadmill in a gym with the treadmill and you moving in opposite directions with the same speed. If you walk in the same direction as the train is going, you will be seen by the trackside observer as moving with a speed of 10 km/hr.

QUESTION:
IF WAVES need a medium to transmit energy but light can travel through a vacuum. Does dark matter have Anything To Do With Lights Ability To Do This?

ANSWER:
There is absolutely no mystery about light waves; electromagnetism is arguably the best-understood theory in all of physics. You may be sure it has nothing to do with dark matter. Dark matter is arguably the least-understood theory in all of physics. There are many features of the universe which do not fit into our current understanding of physics and introducing some kind of particle which interacts with the rest of creation only via gravity would solve a lot of them; all attempts to directly detect dark matter have failed and until there is direct observation we understand nothing. To my mind, failure to observe dark matter may be indicative that we do not understand gravity as well as we think we do.

QUESTION:
Bowling ball vs. billiard ball What would ultimately travel further, a 12 lb bowling ball or a standard billiard ball: if thrown/rolled with the same amount of physical strength/athletic ability, at ideal trajectory for each, on a frozen lake (not without small imperfections but as close to perfect as could be found naturally), under normal atmospheric conditions (Wisconsin in the winter), with little to no wind? Would temperature play a roll in determining a winner? Would the small difference in friction coefficients be significant? Any other variables Etc... My brother and I have been debating this for years while ice fishing.

ANSWER:
(You might not want to read this rather long introductory paragraph if you are just interested in the final answer.) This problem was very interesting to me because I initially thought it was pretty easy to understand. The billiard ball starts out with much greater speed than the bowling ball, jumps into the lead. Neglecting air drag is usually what is done initially in considering such problems and there has to be some kinetic friction for the balls sliding on the ice; but because the kinetic friction is proportional to the weight, each ball experiences the same rate of change of its speed as it slows. Therefore the billiard ball is the obvious winner. When I initially solved the problem this way using reasonable numbers, I found that the bowling and billiard balls had initial speeds of 14 mph and 81 mph, respectively; the bowling ball went 686 ft and the billiard ball went 21,700 ft, a little more than 4 miles! When I was writing the final paragraph I discussed the possible effects of two things I had neglected, rolling of the balls rather than sliding and the possibility of air drag. Just for fun I estimated the effect of air drag and discovered that at the beginning, particularly for the billiard ball, the drag force was considerably larger than the sliding friction. I realized that I had to redo the whole problem, now much more difficult and mathematically involved than originally. Because the air drag estimate I used is valid only if you work in SI units, I will do that throughout and convert to imperial units when needed. The mathematics gets very complicated and I will only sketch my calculations and whoever is interested can fill in the gaps.

First I will tabulate quantities needed for the problem:

We need to quantify what is meant by "…the same amount of physical strength/athletic ability…" I will assume that the thrower exerts a constant force F over a distance d on both balls. Physics says that the result is that a kinetic energy K=½mv² is acquired where m is the mass of the ball and v is the speed it has when it leaves the thrower's hand; this kinetic energy is equal the the work W done which is W=Fd; that is, Fd=½mv². If you solve this equation for v you find the speed, v=√(2Fd/m). I will use Fd=110 J (about 25 lb over 1 m) because this value would give the billiard ball a speed of about 80 mph which seemed reasonable to me.
The masses of the balls are 0.17 kg=6 oz for the billiard ball and 5.4 kg=12 lb for the bowling ball.
I will use a coefficient of sliding friction for each ball which is very small, μ=0.01. Each ball experiences a frictional force of f=μmg=ma (Newton's second law) where a is the acceleration and g=9.8 m/s² is the acceleration due to gravity.
For the air drag I will use the approximation D=¼Av² where A is the area presented to the oncoming air (πR²) and v is the speed. The radii of the balls are 0.0286 m and 0.108 m. As noted above, this equation is only valid for SI units because the factor ¼ includes things like air density, drag coefficients, etc.

We are now ready to start doing the physics. Start with Newton's second law

ma=m(dv/dt)=-¼Av²-μmg

dv/dt=-Cv²-μg (C=¼A/m).

This equation is integrable. The result is

t=tan^-1[v√(C/(μg))]/√(Cμg)|_v(0)⁰.

Evaluating this expression between the limits v=v(0) to v=0 and inverting to solve for v(t) is straightforward but messy. The essential results are illustrated in the two graphs below. The effect of air drag on the bowling ball is modest but noticeable, reducing the time to stop by about 10 s. The effect on the billiard ball, though, is enormous; because of its high speed at the start, it is slowed much more than due to sliding friction alone. Still, it stayed in motion about 20 s longer than the bowling ball and was going faster most of the time, so certainly went farther before stopping. Still, it would be useful to find the position as a function of time to determine how far each ball went.

To find the position, x(t), is straightforward but again messy: integrate the differential equation dx/dt=v(t) where v is the function being plotted in the graphs above. The results are shown in the graphs below. The bowling ball stops at t=54 s at a position x=158 m=518 ft; the billiard ball stops at t=77 s at a position x=535 m=1755 ft. The winner is the billiard ball which goes more than three times farther than the bowling ball! I believe that regardless of any details of the friction and drag forces or how we choose the quantity Fd, the billiard ball will always go farther if the initial kinetic energies are equal.

Finally, I want to discuss rolling vs. sliding. It is really hard to get an object rolling without slipping on a very slippery surface. A sliding ball will not roll until it is nearly ready to stop, and that would have very little effect on my calculations. Also, rolling friction is velocity-independent and proportional to the normal force so it would affect both balls the same.

QUESTION:
How can a photon have the properties of a wave if it is not in an element? It is said to be in a vacuum so ostensibly it is not in an element, but if it is a wave it must have an element. Has science explained this or is it still an unsolved question?

ANSWER:
You have struck on one of the most important realizations in physics: light does not need a medium to move through, it moves through a perfect vacuum. Other waves we know need a vacuum: sound through air (or just about any other medium), water waves could not propogate without water, waves on a guitar string could not exist without the string, etc. But light is unique and does not require a medium. The photon is just the smallest possible piece of light and has wave properties. No unsolved question here!

QUESTION:
I have a question about gravity. In order to general relativity mass bends the space. I saw a simulation of gravity that a man put a mass on a surface like silk. that the mass bends the silk. and we put another mass they attract to each other. that 2D silk is an examinition of our #d world. I wanna know why masses attract to each other. is it becuase of bending space?

ANSWER:
That simulation is a good way to understand how space bending can alter how objects move but keep in mind that it is only a cartoon to illustrate the warping of spacetime. See my faq page.

QUESTION:
If repulsion forces between protons is high why hasn't the nucleus exploded

ANSWER:
It is true that the Coulomb force experienced by protons in a nucleus is very strong. However, the nuclear force at very short distances is stronger and wins the "tug-of-war" and holds them inside. However, this strong force is also a very short-range force and if you pull a proton just outside the nucleus, it will be repelled and fly off. It is also interesting to ask why the nucleus doesn't collapse if the nuclear force is so strong. The nuclear force becomes repulsive if the protons get too close together; this is called the saturation of nuclear forces.

QUESTION:
What would be a ballpark estimate of all the mass converted to energy (lost) by all the fusion reactions in all the stars that are or have ever been in the last 13 billion years (lots of assumptions)? Would this lost mass effect the overall gravitational attraction of the universe? Would it be significant enough to be a factor in the current acceleration of the universe?

ANSWER:
I would not presume to make even the roughest estimate you ask for. However, it is not relevant to the questions you seem to be interested in. According to general relativity, gravitation is caused by energy density, not specifically mass. (Don't forget, mass is just a form of energy, E=mc².) So changes of mass will affect the details of the gravitational field in some volume of space but if you get very far from that volume, the gravity you see originating from that volume will not change.

QUESTION:
Our 5-year-old niece wants to know why it's so hard for her to ride her Big Wheel uphill (3% slope) on her family's driveway. My BSN-RN wife would like a friendly, informative way to break that down for her (Daphne), including whether her weight (50 pounds), her position on the Big Wheel, the coefficient of friction on said drive wheel, and other factors play a part. Said aunt would also like a kid-friendly way to calculate the horsepower necessary for her to ascend that grade on her Big Wheel for perhaps 100' (the driveway's length). No, this is in no way homework. Except it's at their home. And, well, it is work.

ANSWER:
A little tough for a five-year old! Here, maybe, are some suggestions:

Get her to understand Newton's first law: an object at rest or moving with constant speed has all the forces on it cancelling each other out.
- For example, have her imagine imagine sitting still on level ground. Her weight (a force pulling her down) is trying to make her fall down but the ground (a force pushing her up) is holding her up. If the ground disappeared she would fall downward.
Get her to understand Newton's second law. If the forces are not cancelling each other out, the object will start moving and continue to speed up in the direction of the uncancelled forces.
- For example, have her imagine sitting on the trike on the incline with her feet off the pedals or the ground. She will start moving down the incline. What is happening is that her force, which is still straight down, must have a little bit of itself pushing her down the incline. (This is basically a component of the weight but the concept of vectors and their components is likely too hard for a five-year old to comprehend.)
Finally, if, on the incline, there is a piece of the weight which she will have to compensate for in order to keep that force from making her go down the hill: she does this by pedaling to create a force up the incline: the force she generates must be greater or equal to the piece of the weight pointing down the incline. On level ground there is no unbalanced weight so the pedaling is much easier.
Friction, I would opine, is an unnecessary complication.
If she were heavier, the piece down the incline would be bigger so it would be harder to pedal.
(This part is for you, the little girl will not get it.) Your question about the horsepower is incomplete because to calculate the power you need to know the time it takes her to go the 100 ft. Suppose she maintains a speed of about 2 ft/s. Now, the component of a 50 lb weight on a 3% grade is about 50x0.03=1.5 lb so the work done is 1.5x100=150 ft·lb. The time it takes her is (100 ft)/(2 ft/s)=50 s, so the power is 150/50=3 ft·lb/s=0.0055 hp.
Friction has little to do with it because the friction is not significantly different on level ground vs. the incline. Position on the trike plays no role since any change would be the ease of pedaling which would be the same in either case.

QUESTION:
what would a light/sound wave look like in 3 dimensions, all diagrams are in 2d and it just came to mind that it wouldn't be like that in real life

ANSWER:
Here is a cylindrical wave. The blue surfaces represent wave fronts.

QUESTION:
I am currently doing an experiment on the metronome pendulum. As you know a metronome pendulum has two types of pendulum which is the inverted pendulum and simple pendulum. It is called as double-weighted pendulum. This type of pendulum has two weight which is one above the pivot and one below the pivot. In my experiment I want to find the relationship between the varying mass of the top mass of metronome pendulum and its angular frequency but I cant seem to find any formula that describes my metronome pendulum. What formula for angular frequency should I use because from my data, I will be looking for its period of oscillation. There are too many angular frequency formula for different types of pendulum so I am confused on which formula I should be using.

ANSWER:
I will show you how to get a general answer. Then you can apply it to the conditions of your experiment. Newton's second law for rotational motion is τ=Iα=I(d²θ/dt²) where τ is the net torque about the pivot (the blue cross in the figure), I is the moment of inertia about the pivot, α is the angular acceleration, and θ is the angle of the system at some time t. If the system is a pendulum with no forces exerting torques except weights (vertically down), all torques are proportional to sinθ where here θ is the angle relative to the vertical. Now our equation may be written as

(d²θ/dt²)=-(|τ|/I)sinθ

where |τ| is the torque about the pivot when the pendulum is horizontal (θ=π/2). The negative sign results from the fact that the angular acceleration and the angle are always opposite, a restoring torque. This equation is extremely difficult to solve, but if the angle is small (much smaller than 1 radian), you can use the small angle approximation, sinθ≈θ, which gives us

(d²θ/dt²)≈-(|τ|/I)θ

This is the simple harmonic oscillator equation for an oscillating system for which we know the angular frequency, ω=√(|τ|/I). So, let's apply it to your situation as illustrated in my figure. There are two point masses and the mass of the rod itself which I will take as m. The rod has a center of gravity (orange cross) a distance of L₃ from m₁as shown; if your rod is uniform, L₃=L/2. (If the mass of the rod is much smaller than both the point masses, you can approximate m as zero.) Now, since all weights are of the form W=mg, you can write |τ|:

|τ|=g(m₁L₁-m(L₃-L₁)-m₂L₂).

The moments of inertia for the two point masses are

I₁=m₁L₁² and I₂=m₂L₂².

The moment of inertia for the rod is trickier, so to avoid a lot of messy algebra I am going to assume a uniform rod where L₃=L/2. I find

I_rod=(m/(3L))(L³-L₁³)

The total I is just the sum of the three moments of inertia. So, finally,

ω=√[(g(m₁L₁-m(L/2-L₁)-m₂L₂))/(m₁L₁²+m₂L₂²+(m/(3L))(L³-L₁³)]

And, if m can be neglected,

ω=√[g(m₁L₁-m₂L₂)/(m₁L₁²+m₂L₂²)]

QUESTION:
So I have just thought about this, let's just say that hypothetically you were able to fall through the earth completely. I was wondering what the gravity would do to you if you went in one side and came out the other

ANSWER:
See the faq page.

QUESTION:
If everything is expanding, and every galaxy is moving away from the Milky Way, why is the Milky Way and Andromeda predicted to collide in 3.5 billion years?

ANSWER:
See an earlier answer. See a simulation video.

QUESTION:
this is for a horror book I am writing. how fast can a bat fly, if it weights 4500 pounds and is 25 feet 6 inches tall? and in 1 flap of its wings, can rise a rise a quarter, of a mile? also how wide would its wingspan be?

ANSWER:
The best I can do is to estimate how the wings would have to be if the ratio of weight (W) to wing area (A) is the same as a real bat. I find that a typical value for that ratio for bats is about R=W/A=20 N/m²=0.42 lb/ft². So, for your case, A=W/R=4500/0.42≈10,000 ft² or one wing has an area of about 5000 ft². If I model a wing to be a triangle with base B=25 ft and a width H, 5000=½BH=12.5H or H=400 ft, a wingspan of about 800 ft. Since it has the same R as for a real bat, it should be able to fly as fast as a real bat which can be as high as 100 mph.

QUESTION:
I am a part time instructor and one of the things I teach is rigging. An important part of the class is calculating sling stress. I was asked a question that I couldn't quite answer. I don't believe it was my high school or college physics teachers that failed me rather the more than two decades since I sat in a physics class. The question relates to vector forces. If I am hoisting a load of a given weight (say 2000 lbs) and I have two slings that are at a given angle (say 45 degrees) from the load. Each sling would be carrying half the load or 1000 lbs straight up. However, the sling in this example would have 1414 lbs of force (inverse sine if I remember correctly). The question I was asked was regarding a crushing or compression force. Since each sling is carrying 1000 lbs vertical load that means it has 414 lbs of force perpendicular to the vertical. Does that mean that there is 414 lbs of "crushing" force or is it 828 lbs since each sling is pulling towards the center of gravity.

ANSWER:
After an email exchange with the questioner, I was able to determine that "sling" is just a rope or a chain or a string etc. In the diagram I have shown all the forces on the load, the tensions in the slings, T₁ and T₂ and the weight of the weight, W. The magnitudes of the tensions are equal, T₁=T₂ =T. Also shown are the horizontal (x) and vertical (y) components of the tensions; they are T_1x=Tcosθ, T_2x=-Tcosθ, T_1y=T_1y=Tsinθ. So the equilibrium equation is 2Tsinθ-W=0; therefore T=W/(2sinθ). So, for your example, sinθ=cosθ=1/√(2), W=2000 lb, and T=1414 lb. Now, your interest is in the horizontal components; each is Tcosθ=W/(2tanθ)=1000 lb "crushing force" on each side. Your main error is that you treated the vector forces as scalars, you assumed T=T_y+T_x where in fact T=√(T_y²+T_x²).

QUESTION:
Since everything in the universe is always moving, is the idea of being still/idle/stationary just an illusion?

ANSWER:
I would not put it like that. If you are in a system where Newton's first law (if the net force on an object is zero, it will remain at rest or moving with a constant velocity) is correct, you may think of yourself at rest. This is called an inertial frame of reference. But the catch is that this is not the only frame of reference in the universe where Newton's first law is true, any other frame which moves with a constant velocity relative to yours is also an inertial frame. In other words, there is no such thing as absolute rest. A frame accelerating relative to yours, however, is not an inertial frame.

QUESTION:
I am a cancer patient about to receive Y-90 treatments. If Y-90 has a half life of 64 hours: 1. When does that time clock begin running and 2. How can they ever have a full strength dose on hand at any given time?

ANSWER:
⁹⁰Y is the decay product of ⁹⁰Sr which has a half life of about 29 years. 90Sr is an abundant byproduct of the fission of uranium and therefore available in the waste of reactors. When the ⁹⁰Y is needed it can be chemically separated from the ⁹⁰Sr. I am sure that the hospital cannot keep a supply on hand and will have it delivered when it is needed for your treatment. It does not matter how long it has been since it was separated, only that the radiation level be correct for the prodedure. It probably arrives with a level too high and they wait for it to be at the needed level.

QUESTION:
I am struggling with the concept of relativity, as it relates to time. Not in terms of the underlying principle or the mathematics. These have been confirmed experimentally and are now in everyday use through technologies such as satellite navigation systems. My concern relates to the way that relativity treats time as a variable rather than an absolute quantity. It seems to me that we can only measure or experience time by reference to some physical process or change, whether that is the oscillation of a quartz crystal or the lifetime of a muon! Any experimental proof of time dilation as a result of the effects of either velocity or gravity really just relates to the way that we experience the passage of time and does not exclude the possibility that for the universe, as a whole, time is absolute and unchanging, passing in a constant fashion regardless of relativity and whether we measure it or not. Therefore, although relativity theory works in practice, this is only because it deals with our limited understanding of, and ability to measure and/or experience, the passage of time. Is this nonsense or is it a possibility? It follows from this reasoning that we can never prove experimentally that time either speeds up or slows down, only that the rate of how we measure or perceive time can vary. It also implies that time (and indeed space) are concepts that we will never fully explain as they ultimately cannot be qualified or quantified by measurement or mathematics.

ANSWER:
You are correct that "…time is absolute and unchanging, passing in a constant fashion…" but only in your frame of reference; any clock at rest relative to you runs at a constant rate. But, what special relativity tells us is that clocks not at rest relative to us do not run at the same rate as ours. I have always felt that the best way to convince someone that this is the case is the light clock. In order that this example is convincing to you, you must accept that the speed of light is a universal constant in all frames of reference; but this is an experimentally well-verified fact and also is a consequence of the principle of relativity—that the laws of physics are the same in all inertial frames of reference.

QUESTION:
SINCE FREE FALL DONT NATURALLY OCCUR ON EARTH BECAUSE FLUID FRICTION IS PRESENT IF YOU DROP A BOWLING BALL AND A BASEBALL OFF A TOWER OF PISA WHICH WOULD LAND FIRST

ANSWER:
The (upward) drag force on a falling sphere of radius R and speed v in air at sea level may be approximated as F=¼πR²v²=0.79R²v² (this is correct only in SI units); the (downard) force of the weight W on an object of mass m is W=mg. The net force is the mass times the acceleration a (Newton's second law), ma=-mg+0.79R²v². So as the object falls it goes faster and faster until v is large enough that it falls with a constant value speed v_t (a=0), v_t=[√(mg/0.79)]/R. For a baseball, m=0.144 kg and R=0.037 m, so v_t^baseball=9.28 m/s. For a bowling ball, m=8 kg and R=0.12 m, so v_t^{bowling ball}=83.0 m/s, nearly ten times greater than the baseball. So the baseball stops accelerating sooner than the bowling ball and loses the race to the ground.

QUESTION:
My 8 year old asked me if the cycle of the universe expanding and contracting will ever end?

ANSWER:
What makes you and your son think that the universe is in such a cycle? The ultimate fate of the universe is one of the most important questions in cosmology and nobody knows the answer. I believe most cosmologists believe that the universe will continue expanding forever. Eventually the supply of hydrogen and helium in the universe will be exhausted (fused into heaviers elements) and stars will no longer exist. The universe will be dominated by black holes which will eventually decay away by Hawking radiation, so the universe will be a very dilute, cold, dark place filled with radiation. To get more information, check out the Wikepedia article on the fate of the universe.

QUESTION:
My son has a question. A shadow is long or short, wide or narrow. He thinks this seems like area (taking up space). But the real question is... can you have a shadow without matter? Because if you can't have a shadow without matter, then doesn't that mean the shadow is actually matter? (I have to ask because I'm not sure how to answer this; I suppose the shadow is actually the part of the matter that doesn't have light reflecting off of it...? Or how do I answer this for him?)

ANSWER:
A shadow is not matter; it is not anything, it is a region in which light illuminating something is blocked by some obstruction. You might say that a shadow is the lack of anything, light which might have otherwise illuminated where it is. And there are degrees of "shadowness". If all the light illuminating an area is blocked by the obstruction, it is called an umbra; if only part of the light is blocked it is called a penumbra. (Umbra is Latin for shadow.)

QUESTION:
U recently answered a question regards Earth's precession = 26,000 yrs. Can u show what specific equation(s) used to yield this time? I doubt that a single equation was used.

ANSWER:
Just like the precession of a top is due to the torque exerted by its own weight, the precession of the earth is due to torques on the earth, mainly by the sun and the moon. Your equations may be found in this Wikepedia article.

QUESTION:
On an ordinary day as one goes upward from the surface of the ground the electric potential increases by 100 volts per meter, this means that outdoors the potential of your nose is 200 Volts higher than that at your feet. Then why is it that none of us get a shock when we go out in the street?

ANSWER:
As is often the case, the most lucid answer to your question can be found in the Feynman Lectures.

QUESTION:
Why doesn't the earth just stop spinning and orbiting don't you need energy for motion where does the earth gets it's energy and is the earth in perpetual motion?

ANSWER:
You are hitting one of Isaac Newton's most important discoveries—inertia. It says that you do not need to exert a force (torque) to keep an object moving in a straight line (rotating about an axis) to keep it going; this means, also that the energy it has by virtue of its motion will not change. So the rotating earth keeps rotating since there are no torques on it*. The earth is in a circular orbit† around the sun and so its orbital motion keeps going since, even though there is a force on the earth, there is no torque.

*Actually, the moon does exert a torque on the earth which is causing the spinning to get smaller, but the change is so tiny that it takes millions of years to be significant.

†The earth's orbit is not exactly circular. When it moves closer to the sun it speeds up, when it moves farther from the sun it slows down by exactly the same amount, so the orbit just continues forever.

QUESTION:
With the devastating tragedy that happened in Lebanon, there has been some videos surface of the explosion. One such video is of some ladies in a shop, the pressure wave hits the shop and the lady outside the shop doesn't get thrown back but inside the other lady does. What is the explanation here??

ANSWER:
Note that the glass doors are closed. Outside the front of the pressure wave hits, but it takes some brief time to reach its maximum. However, the pressure difference between inside and outside is not large enough to break the glass until it is near its maximum, so the pressure difference changes much more quickly so the air rushes in quickly. I will admit that this is just an educated guess!

QUESTION:
If electricity always take the path of least resistance, why does a lightening discharge form a zigzag path to earth and not straight down which would be the shortest distance?

ANSWER:
Because air is not just a uniform homogeneous medium. There are local fluctuations in temperature, humidity, density, wind speed, and composition which makes the path of least resistance at any instant, not a straight line.

QUESTION:
how momentum is conserved of both objects with same masses moving opposite direction to each other collide to a point and at same time both objects chemically combined to each other?

ANSWER:
In an isolated system, linear momentum is always conserved; this is because the definition of linear momentum is designed to be conserved in the absense of any external force. This is also true in special relativity where the linear momentum is not p=mv but rather p=mv/√[1-(v²/c²)] where c is the speed of light. In the event of chemistry going on, there is either energy gained (endotermic) or lost (exothermic). If lost, the momentum of the radiation has to be taken into account. If gained, the energy will be taken from the kinetic energies of the incident objects but momentum will be conserved.

QUESTION:
Does precession and nutation ( or anything else ) affect the axis of the earth?

ANSWER:
Precession of the earth's axis is caused mainly by torques exerted on the earth by the moon and the sun. The period of precession is 26,000 years. But precession does not cause the actual rotation axis to change. What causes the axis to change (such that the geographical positions of the poles would change) is thought to be three things:

glacial ice melting and sending its water to the oceans,
glacial rebound which is the raising up of the land previously supporting the melting glacier, and
tectonic motion, the drift of large land masses.

QUESTION:
The momentum transmitted to the golf ball comes from the club head and,to a lesser extent, from the club shaft. Golfers are instructed to hold the club very loosely. Thus, it seems, no momentum is transmitted from the arm. What if the golfer instead holds very tightly to the club? Will the momentum of the arm be transmitted to the golf ball?

ANSWER:
The physics of a golf swing is much more complicated than you might think. From the little research I saw, your "hold the club very loosely" is an oversimplification. The club needs to accelerate very quickly on the way to the ball and that acceleration is only going to come from the torque you provide. What should happen is that, just before impact, your wrists must relax. There is an excellent discussion on the golf swing which, for the first half is fairly conceptual and the second half goes into the detailed physics analysis of the swing.

FOLLOWUP QUESTION:
I understand that the standard golf swing depends on uncocking the wrists to generate velocity at the moment of impact. Moe Norman, a Canadian golfer now deceased, was the best ball striker in the history of golf. Moe used a completely different swing that he developed. Among other things, it involved holding the golf club tightly. Thought experiment: The shaft of the golf club is fused to the golfer's arm and runs all the way up to the shoulder. That is, there is no wrist play at all. I understand that such a set-up will generate less velocity than a hinged wrist. Therefore, the 'v' in 'mv' will be lower. My question is whether the 'm' will be higher. Given that the golfer is now swinging a much more massive club, albeit from the shoulder, I posit that the mass striking the ball is greater. Take the center of gravity of the club-arm, calculate its velocity, multiply by the mass of the club-arm, and one has the momentum that is transmitted to the ball (I think). This may or may not be as great as the momentum of the faster wrist-hinged swing. I just want to know whether the 'm' will be greater with this fused club.

ANSWER:
I believe that there is no way to understand the club as a point mass, so to talk about its mass in a collision is meaningless. Think of it as a machine which imparts momentum to a small mass by exerting a force on it over some short time. I think it probably boils down to having the machine achieve the greatest possible velocity when it hits the ball; if you can achieve that by holding the club more tightly, go for it! It was interesting to learn a little about Moe Norman of whom I had never heard.

QUESTION:
When a golf club hits a golf ball, part of the momentum of the golf club transfers to the golf ball. The golf ball, being light, takes off at a velocity greater than the club head speed. What if the golf club is accelerating at the point of impact? Will the ball take off faster (and go further) than when it is hit at the same impact velocity by a club that is not accelerating? Note: amateur golfers tend to reach maximum velocity at the point of impact. Pros reach max velocity after impact. Pros do swing faster, which imparts more velocity to the ball. I would like to know whether their acceleration adds even more velocity.

ANSWER:
What will determine the exit speed of the ball is the speed of the club at impact. The impact time is approximately Δt=0.0005 s. How big would the acceleration need to be in order to significantly change the speed over this time? A typical speed of the club head is about 150 mph, about v=70 m/s. Suppose that the speed increased over the impact time by Δv=1 m/s. Then the acceleration would have to be a=Δv/Δt=1/0.0005=2000 m/s²; this is about 200 times greater than the acceleration due to gravity. We could estimate the acceleration by guessing that the club took about 0.1 s to go from zero to 70 m/s, a=700 m/s². So the speed of the club might increase by 700x0.0005=0.35 m/s and the average speed during impact would be about 70.2 m/s. My feeling is that this would have a negligible effect on the speed of the ball.

FOLLOWUP QUESTION:
I did some more research and I have a follow up. This article states that Force equals mass times acceleration. It indicates that applying a force to an object over time creates momentum. Therefore, it seems to me that a club head that is accelerating at the point of impact transmits Force and, therefore, momentum to the golf ball. And that this momentum would be in addition to the momentum of the club head. A club head that is not accelerating will transmit no force to the golf ball. It seems to me that a club head accelerating is going to hit the ball further, velocity at impact being equal.

ANSWER:
Sorry, but you have this all wrong. (This is what comes from using formulas when you do not really understand what they mean or when they are applicable!) F=ma is Newton's second law and simply says that if you push or pull on a mass it will accelerate. Indeed, if you apply a force over a time you will accelerate it and therefore change its momentum. But these do not imply that the source of the force itself needs to be accelerating. Here is what happens: when the club strikes the ball, it exerts a force on the ball; Newton's third law says that if the club exerts a force on the ball, the ball exerts an equal and opposite force on the club. For the short time that they are in contact (after which the forces disappear), the ball will speed up and the club will slow down if there are no other forces on it (which may be the case*). If the average force they exert on each other is F and the time of contact is t, the ball will acquire a linear momentum of p=Ft; the ball will experience a change in its momentum but by how much is not so simple since other forces act on it. Note that F=p/t=mv/t, so the smaller t, the larger F, all else being the same. In my answer to your original question, using v=70 m/s and t=0.0005 and noting that the mass of a ball is about m=0.046 kg, F=0.046x70/0.0005=6,440 N=1448 lb.

*If the club is accelerating when it strikes the ball there must be some force on it—ultimately that comes from you.

QUESTION:
I am writing a video response to Dr. William Lane Craig, a well known apologist, and so I am answering every position he states from a debate between him and Christopher Hitchens at Biola university some years ago. I write to you now because Dr. Craig says something that I don't understand. He states, "First, when the laws of nature are expressed as mathematical equations, you find appearing in them certain constants, like the gravitational constant. These constants are not determined by the laws of nature. The laws of nature are consistent with a wide range of values for these constants." I don't understand this at all.

ANSWER:
(This is not the whole question submitted, but gets to the heart of what the questioner wants to know. Reminder that site ground rules specify "…concise, well focused questions…") I consider that the most important "laws" of nature are not equations, they are proportionalities. In order to keep this discussion focused on my basic description of nature, I will focus solely on classical physics to make my points. In physics we begin with three fundamental concepts to lay the foundation of describing nature: mass, length, and time. In the SI unit scheme we choose kilograms (kg), meters (m), and seconds (s). With the chosen units we can define velocity as the rate of change of position with units of m/s; then we can define acceleration as the rate of change of velocity with units (m/s)/s=m/s². So if an object changes its speed from 2 m/s to 6 m/s in a time of 2 s, its acceleration is 2 m/s². Mass is trickier to understand but it is a quantity which measures how resistant an object is to being accelerated if you push on it; it is harder to accelerate an object of mass 1000 kg than it is one of 2 kg. Note that we have not yet quantified that push (or pull) which we normally call force. However we can certainly imagine figuring out a way to push or pull on something twice as hard, or three times as hard, etc. Whatever force is, suppose we push on something with a constant force F and vary the mass; we will find that if we double the mass we halve the acceleration, if we halve the mass we double the acceleration, if we make the mass 10 times larger, the acceleration is 1/10 of its original value, etc. We have found that, F being constant, acceleration a is inversely proportional to mass, a∝1/m. Now suppose we vary F but keep m constant; we find that if we double the force we double the acceleration, etc., i.e. a∝F. We can now put the two together and get a∝F/m or F∝ma. This is what I consider to be Newton's second law; it tells us an important connection of how quantities depend on each other, it is a law of physics; and, you really did not have to have defined the meter and second and kilogram for it to be true, you just had to understand conceptually what mass, length, and time are. If you know even a little physics, you do not recognize this as Newton's second law—any textbook will tell you that it is F=ma. Now, how can one turn a proportionality into an equation? It is simple, just introduce a proportionality and voila! F=Cma where C is an arbitrary constant since we have not defined how we will measure F. Don't think of it as a "fundamental constant" because if we had already defined how to measure force, we would have to measure C. For example, if we had defined a unit of force to be a pound but measured m and a in SI units (kg and m/s²), F=ma would not be a valid statement of Newton's second law.

Now let's discuss an example of when a constant is a fundamental constant. Newton's law of gravitation expresses the magnitude F of the equal and opposite forces exerted on each other for two point (or spherical) objects of masses m₁ and m₂ separated by a distance of r: F∝m₁m₂/r². Now, to make this an equation, we must introduce a proportionality constant G: F=Gm₁m₂/r². But can we choose it to be whatever we like? No, because there is nothing in this proportionality which is undefined; we can take two 1 kg masses, separate them by 1 m, and measure the force between them (a really hard experiment!). In other words, we must measure the constant G. This is a true fundamental constant of nature, it measures the strength of gravitation. Of course, its numerical value depends on how we measure mass, length, and time, but it is still a universal constant. In SI units it is 6.67x10^-11 N·m²/kg².

You might be interested in two earlier answers, 1 and 2, along similar lines as yours.

QUESTION:
I wondered what happens if one would make a magnet spin really fast. Could it be theoretically possible that it could create visible light.

ANSWER:
The frequency range of visible light is about 4-8x10¹⁴ Hz, so you can be sure that you cannot do this with any macroscopic magnet. One way to get magnetic radiation is to fabricate something called a split-ring resonator (SRR) but technical problems limit SRRs to about 2x10¹⁴ Hz, near infrared. Another technique uses spherical silicon nanoparticles and these can generate visible magnetic light. The method is too technical to discuss here, but you can read about it at this link.

QUESTION:
i had a doubt, to detect an inertial frame we need to define 0 force, but to define 0 force we need an inertial frame,0 force is defined as the sum of real forces should be 0, and we can identify real forces if we believe that the real forces drop with distance,and this could be a possible solution to the above problem, but it based on an assumption, and even if we consider that we cannot detect an inertial frame, and all the physics upto special relativity is just based on if there is an inertial frame, then how come we could do experiments to confirm the theory and how did physics work uptill general relativity, if we cannot solve this basic conceptual problem.

ANSWER:
Technically, there is no such thing as an inertial frame. No matter where you go in the universe there are always electromagnetic and gravitational fields. That does not mean we cannot define an inertial frame as one in which Newton's laws are true at low velocities. In fact we can do better by defining an inertial frame as one in which the total linear momentum (relativistic definition) remains constant; then you are not confined to low velocities. Then we will find that very good approximations to inertial frames can be found in nature. There is nothing wrong with basing a theory on an idealized (fictional) concept as long as the ultimate theory agrees with experimental results in the real world.

QUESTION:
The idea of dark matter and dark energy is puzzling me. It is understood that dark matter acts like glue to hold galaxies together. On the other hand, dark energy is responsible for expansion of universe. Scientists say inside galaxies dark matter overcomes dark energy so gravity wins and keeps galaxies together but when it comes to intergalactic space, it is said that dark energy overcomes dark matter and wins the fight, so galaxies are moving away. How do you explain this contradiction? Why dark energy wins in intergalactic space but not inside the galaxies. In other words, what makes dark matter overcomes dark energy in galaxies but loses in the space between galaxies.

ANSWER:
Even though I state on the site that I do not do astronomy/astrophysics/cosmology, I will take a stab at this one. Of course, keep in mind that nobody knows what dark matter or dark energy are in any detail. Dark matter, as the name implies, is thought to be some kind of mass and therefore subject to gravitational forces. It therefore would be not surprising to find it more concentrated in the vicinity of large masses like galaxies; so its density is likely to be smaller in intergalactic space. Even less is known about dark energy but, if it is anything like uniformly distributed, it is more likely to lose a "tug-of-war" with dark matter inside a galaxy than outside.

QUESTION:
What happens to the gravitational effect of mass when it transforms into energy, as in e=mc^2?

ANSWER:
In general relativity, our best theory of gravity, the bending of spacetime, which is what gravity is, is not caused only by mass. Any local energy density will cause gravitation.

QUESTION:
I would like to ask about gravitational mass. I know inertial mass is changing by motion (speed) according to m=mo/(1-v2/c2)^0.5 And also that is inertial mass which sits in E=mc2. If the statements above is correct, now how about gravitational mass? Does it change with motion (speed)? And what mass should be used for general gravitational formula F=GmM/r2? should we use mo (rest mass) regardless of speed of the object? Or should we use m=mo/(1-v2/c2)^0.5 to substitute in F=GmM/r2? In other words does mass equivalence principle (inertial mass=gravitational mass) hold in hight speeds?

ANSWER:
Read the answer to the previous question. The moving mass has more energy than the stationary mass and therefore has a stronger gravitational field as measured by a stationary observer. Newton's gravitational equation is amazingly accurate for speeds small compared to the speed of light. However, if you are at very high speeds you should not use it at all. The whole notion of force is, itself, not useful in relativistic circumstances. We might ask why force is a useful concept in classical physics. Newton's second law, the central concept in classical mechanics, is F=ma. Why? If someone is moving past you and measures the acceleration a' of something in your frame, she will measure exactly the same value as you. Therefore you will both conclude the same force is being applied to m, if a=a' then F=F'. But if relative speeds are not small, a≠a' so Newton's second law is no longer true. Instead we rely more on conservation principles more in relativity theory. In particular, we want to redefine momentum so that it is conserved in a closed system.

QUESTION:
I have recently learnt about the LIGO detector and watched a few videos on how it works, I understand how they detect the stretching and contracting of space time due to the gravitational wave only stretching and contracting a few hundred times per second and the new photons entering this space must travel farther or shorter deviating from the normal time travelled. I would like to ask how these new photons enter this stretched space time since the gravitational wave itself is travelling at the speed of light does that not mean the stretched space will either move with a certain packet of photons, and since the wave travels at light speed, there wont be enough contractions to allow detection to occur.

ANSWER:
You just make this too hard to visualize thinking of photons. Think instead as electromagnetic waves. (Although the speed of the gravity wave does not matter for the interferometer to work, it is just as if somebody were jiggling the mirror ends, I want to note that it is only assumed that the speed of gravity is c; the speed of gravity has never been measured, we just know that it is very fast. Since the gravitational field has never been quantized, we can only assume that the graviton has no mass. Note that for decades it was assumed that neutrinos had no mass, something we now understand is not true.)

QUESTION:
Who first derived the relativistic energy-momentum relation E²+p²c²=m²c⁴ and in what publication? Wikipedia says that it was Dirac in 1928, but I cannot find evidence of this in his famous 1928 paper, "The Quantum Theory of the Electron."

ANSWER:
As far as I can tell, Dirac's 1928 paper used the energy-momentum relation as a jumping off point for his derivation of the Dirac equation. Certainly this equation was known long before 1928 since special relativity itself was introduced in two papers by Einstein in 1905. The first paper did not mention momentum at all. In the second paper he shows that if a particle of mass m radiates energy L that the mass changes its kinetic energy by L/c², hence E=mc², but does not mention momentum. Finally in 1907 he writes an article in which he shows that if relativistic momentum is p=mv/√[1-(v/c)²], then it is a conserved quantity as in classical Newtonian physics. From here, and knowing E=mc²/√[1-(v/c)²], it is straightforward to get the energy-momentum relation.

QUESTION:
Why would lifting my feet off the ground make me heavier. Let's say I were to do a push up while my friend is on my back for extra weight. If the friend was to plant her foot on the ground, why would the push-up become easier.

ANSWER:
In the first figure I show all the forces on the man in yellow. They are: N is the force which the ground must exert up on the man, W is his weight, and F is the force which the woman exerts down on the man. (I have drawn N as one vector, but it is really distributed among his two feet and two hands. Nevertheless, the size of N is proportional to the force he must exert to lift himself.) The man is in equilibrium, so the forces on him must add to zero, N-W-F=0 or N=W+F. In white are the forces on the woman: w is her weight and f is the force which the man exerts up on the woman which by Newton's first law equal and opposite to the force which she exerts down on the man so F=f. Since she is also in equilibrium, the sum of the forces on her must add to zero, so f-w=0 or f=w=F. So, finally, we see that the total weight the man must cope with is the sum of his and the woman's weight, N=W+w.

So now I put a blue brick under the woman's foot so that it rests on the brick. This is a new force n up on her, shown in red. Each person's weight is the same as before, your weight is just the force down due to gravity. But now there are three forces on the woman adding up to zero: n+f '-w=0 or f '=w-n. The force f ' exerted up on her by the man, which has the same magnitude of the force F ' which she exerts down on the man, is smaller than before. So now, N '-W-F '=0 or N '=W+F '=W+w-n. He has a smaller total force to contend with than before.

The mistake you made is that you assumed that the force down on the man was the woman's weight. But the woman's weight is not a force on the man, it is a force on the woman. This is accidentally correct in my first example because if only the man is supporting her, it just happens that the force she exerts down is equal to her weight in magnitude. But in the second example the brick is supporting part of her weight so the man supports less. She does not become lighter!

QUESTION:
I am writing a fantasy novel currently, and at the ending a giant Dragon, with scales made out of stone is falling into the sea infront of a city and I'm imagining a tsunami destroying the city. The dragon weighs around 2,000 tons, how high would the wave be and how far would it reach inland? (the city is basically a flat plain)

ANSWER:
Well, I have to make some wild approximations to address this at all. I will perhaps get you within an order of magnitude of how big the wave might be. Maybe I should sort of do a rough general case first and then I can throw in some reasonable numbers. If the dragon drops from a height h and has a mass m, then the energy she starts with is E₁=mgh, where g is the acceleration due to gravity. When she hits the water she will have a smaller energy because of air drag falling down and when she comes to rest she will lose some energy to heat and sound and damage to her body; I will say that a fraction f of the original energy goes into the energy E of the wave created, E=fE₁. Now I will assume that all this energy goes into a circular pulse which has a width of w and a length of 2πR (circumference of a circle) where R is the radius of the circle at the time of interest, namely when the wave hits the shore; so R is the distance from shore where the dragon hit the water. Now, I found an expression on Wikepedia which relates the energy of a wave to its height: E/A=ρgH²/16 where A=2πRw is the total horizontal area of the wave, H is the height of the wave, and ρ=1000 kg/m³ is the density of water. If you put it all together you will find H=√[8fmh/(ρπRw)]. Suppose h=5000 m, m=2x10⁶ kg (2000 metric tons), f=½, and w=20 m; then I find H≈25 m. This is in the same ballpark as the largest tsunami wave ever observed which was about 100 ft. There is no way I could estimate how far inland the wave would travel; it would depend a lot on the terrain, obstacles, etc.

QUESTION:
This question is in reference to quantum entanglement. When a Super positioned photon is measured to determine spin does it's spin stay in that orientation as long as they a measuring it or does it immediately go back to a Super positioned state? In other words if you determined the spin of a quantum entangled particle at say 12:00 pm and constantly measured it, would it's spin continue to point in the same direction at say 12:02 pm. or is the measurement only good for the exact moment it was initially measured?

ANSWER:
When you observe it, you put it in a single state (and simultaneously, put the other entangled photon in a single state). Unless it interacts with something else later, they remain in states you put them, they do not reëntangle.

QUESTION:
What is the maximum distance between two electrons where they will notice each other? They would both be at rest to each other in a vacuum with no external stimuli or forms of energy. At what distance do the electrons "See" each other.

ANSWER:
This question has no meaning because "notice each other" is not quantified. In principle, the Coulomb force extends all the way to infinity. You could, for example, ask at what distance would the force each electron feels would result in an acceleration of 1 mm/yr²=[1x10^-3m]x[(1 yr)x(365 day/yr)x(24 hr/day)x(3600 s/hr)]^-2≈9x10^-22 m/s². In general, the force is F=ke²/r²=ma, so r=√[ke²/(ma)] where k=9x10⁹ N·m²/C², e=1.6x10^-9 C, and m=9x10^-31 kg. I calculate, approximately, that r≈5x10¹¹ m≈300,000,000 miles which is about 3 times the distance to the sun. Of course, you could never do such an experiment since you would need to be in a universe which contained nothing but these two electrons.

QUESTION:
Aren't "constants" simply a "fudge number" to make equations work? It seems to me, constants are values of a concept we have yet to identify or understand, but need to make equations with known concepts and values work out. Since these equations work correctly with a variety of known variables, they are generally accepted. It seems to me, non-electrical magnetism (i.e. that which is retained in magnetic material like iron) and gravitation have a variety of descriptions and equations which predict their effects--yet we still are devoid of actual cause.

ANSWER:
Constants are not just "fudge numbers" as you suggest. They can be, but in general constants play a very important role in physics. I will give you a few examples.

The laws of physics are stated most elegantly as proportionalities rather than equations. For example, Newton's second law states that the acceleration (a) of an object is directly proportional to the applied force (F) and inversely proportional to the mass (m), a∝F/m; so you double the acceleration if you push twice as hard and halve it if you double the mass. Now, to calculate we prefer to have equations rather than proportionalities, so we introduce a proportionality constant, call it C, a=CF/m. What does C mean? Since we know how to measure a (m/s²) and m (kg), your choice of C determines how we will measure force. I would like the force to have the magnitude of 1 if a=1 m/s²and m=1 kg, so I choose C=1. The constant C is not a fudge factor, rather its choice defines how we measure forces. (We call the unit kg·m/s²a Newton, N.)

Newton also discovered the universal law of gravity: if two masses (point masses or spheres) m₁ and m₂ are separated by a distance d, they exert equal and opposite attractive forces on each other the magnitude of which is F; then F∝m₁m₂/d². So the equation for universal gravitation would be of the form F=Gm₁m₂/d². where G is some constant. But we know how to measure mass and distance and force, so we cannot choose G to be any old thing we want as we did for Newton's second law, we must measure it. It turns out to be G=6.67x10^-11 N·m²/kg². This is one of the most fundamental constants in all of nature and most certainly not a "fudge factor".

Constants are often used to quantify a particular situation. For example, the frictional force f of one object sliding on another is found, approximately, to be proportional to the force which presses one object to the other (often called the normal force, N). This is not a physical law, just an approximation of experimental measurements, and it obviously involves only the magnitudes of the forces since their directions are perpendicular to each other. So, including a proportionality constant μ, called the coeficient of kinetic friction, f=μN. This constant tells you how slippery the surfaces are; its value for rubber sliding on ice will be much smaller than for rubber sliding on asphalt.

Sometimes, as you suggest, constants are added to fit data and their physical meaning is unknown, you might label such constants as "fudge factors".

You may be interested in learning about Planck units discussed in an earlier answer. where new units are expressed by combinations of the five fundamental constants of nature.

QUESTION:
In a example of a electrical generator. Central in the generator are rotating magnets. I understand that as the magnet moves the cores of the surrounding coils will react producing a magnetic field. Also the copper wire winding around the coil will react. My question is does the copper wire winding react to magnetic field according to the field produced by the core or the moving magnet ? In a lenz law sense. Plus would I be correct in thinking if there is no circuit on the copper winding there no organised field would form on the copper wire winding itself.

ANSWER:
The best way to understand the priciples is to look at the simplest possible generator. The figure shows a generator consisting of a single loop rotating in a magnetic field which is approximately uniform. There would be no difference in the results if it were the magnets rotating around the coil as you describe. Since the induced EMF in the loop is proportional to the time rate of flux through the loop and the flux is proportional to the cosine of the angle θ between the field and a normal to the area of the loop, the induced EMF will be sinesoidal. The angle may be written as θ=ωt where ω is the angular velocity of the loop (or magnets) and t is some arbitrary time, so the voltage is proportional to cos(ωt). If there is a load across the terminals, and therefore a current through the loop, there will be a field due to the current which does not affect the output voltage if the source of power maintains a constant angular velocity. If you are drawing power from the generator, it is harder to "turn the crank" than if there is no current flowing. If you need detailed information on "real-life" generators, it is more an electrical engineering question than physics.

QUESTION:
How did Einstein derived general relativity math when he understood that the gravity is just the space bending around an object how did he applied this to the world of math?

ANSWER:
You can learn about how Einstein struggled with the mathematical methods necessary to fully describe general relativity and with which mathemeticians he consulted in his biography by Walter Isaacson, Einstein: His Life and Universe.

QUESTION:
I have been thinking about clocks lately and found myself in a sort of a pickle over the velocity of a dial. (I am not native so sorry if my description makes it very complicated). Suppose we have a disc with a dial starting at its center. The dial draws two circles on that disc as it turns. The first circle has its radius equal to r, whereas the second circle has a radius of 2r. Now suppose that 1 full turn takes 1s (which would be the same for both circles since they are being drawn by the same dial). Now because of the difference of radii, there is also a difference in their circumference c. And so we've got t=1s, c=2πr and c'=4πr (2π2r). Now here's the question - if the time is the same, but the circumference or distances are different does that mean the velocity of these two points on the same dial is different? How is that possible since the dial turns with a set velocity which in my understanding would be the same for each point on that dial?

ANSWER:
It is simply because all points on a rotating rigid body have the same angular velocity, (revolutions per second, e.g.) but not the same translational velocity (miles per hour, e.g.). In general, v=rω where v is the translational speed, r is the distance from the axis of rotation, and ω is the angular velocity in radians per second.

QUESTION:
I was just wondering why does the centripetal acceleration formula work a=v^2/r?

ANSWER:
Why does it work? It "works" because it is correct. Maybe you wanted to ask "where does it come from?" or "how is it derived?" I will give you a brief standard derivation.

On the left of the figure I have drawn the particle moving with constant speed v around a circle of radius R. In some time interval Δt the particle moves through an angle theta and has velocities v₁ and v₂ but both speeds are equal to v, v₂=v₂=v. On the right I have placed the velocities tail-to-tail and drawn the difference vector v₂-v₁=Δv. So now I see two isoscoles triangles, each with the same angle between their equal sides; they are therefore similar triangles and so we can write v/Δv=R/Δs. If I now rearrange and divide each side by Δt, I find Δv/Δt=(v/R)Δs/Δt. Now, Δv/Δt is the magnitude of the average acceleration; to get the instantaneous acceleration, we must take the limit as Δt approaches zero. But, when Δt approaches zero, Δs/Δt approaches v. So, finally, a=v²/R.

QUESTION:
Is Planck time a concept derived from the theory of relativity or its premises?

ANSWER:
No, that is not where the concept came from. The origin of Planck units came from the desire to have a system of units which are based only on constants of nature, not on the specific units like the meter, the second, etc. You take the five universal constants:

the speed of light in vacuum, c,
the universal gravitational constant, G,
the rationalized Planck's constant, ℏ ,
the Boltzman constant, k_B, and
the Coulomb constant, k_e=1/(4πε₀).

You now form combinations of these constants which have the correct dimensions of the units you want:

length,
mass,
time,
temperature, and
electric charge

I have copied the table from Wikipedia showing the values of these Planck units in SI units:

It is hypothesized that, at distances smaller than l_P=1.6x10^-35 m, the usual physics as we know it will not work. I think you might say that the origin of the idea of Planck units is quantum field theory.

QUESTION:
A toy top is a disk-shaped object with a sharp point and a thin stem projecting from its bottom and top, respectively. When you twist the stem hard, the top begins to spin rapidly. When you then set the top's point on the ground and let go of it, it continues to spin about a vertical axis for a very long time. What keeps the top spinning?

ANSWER:
There is a property of spinning objects called angular momentum. For example, the angular momentum of your top is a vector approximately equal to ½MR²ω where M is the mass of the top, R its radius, and ω is the rate at which it is spinning; the direction of the angular momentum vector is straight up if it is spinning counterclockwise if viewed from above, straight down if clockwise. There is a physical law which states that if there are no torques on a spinning object, its angular momentum never changes. There are no torques on the top if its spin axis is vertical and so it does never stops.

QUESTION:
The third dimension is 3D (spheres, etc.). The first dimension is a dot. Everything that has a front and back, has an edge. So isn't a dot 3D?

ANSWER:
A dot has zero dimensions. The formal definition of the dimensionality of a space is an answer to the question "how many numbers does it take to specify the location of a point in that space?" You may heard of Cartesian coordinates, (x,y,z); they were named in honor of the 17th century philosopher and mathematician René Descartes. Legend has it that he was once watching a fly buzzing around his room and asked "what is the minimum number of numbers I must specify to describe the position of the fly at any time?" He figured it was three: the distance up from the floor, the distance from the back of the room, and the distance from one of the side walls; his room is said to have three dimensions. One dimension is a line; here you simply measure the distance from one point on the line to wherever the particle is. The line need not be a straight line. A circle is one-dimensional and the location of a point on the circle is usually specified by an angle relative to some point we call zero. Two dimensions is a surface. The surface of the earth is two-dimensional, the position being angles, latitude and longitude. One surface of a flat sheet of paper is two-dimensional and the two numbers are usually Cartesian coordinates (x,y). The spatial universe in which we live is three-dimensional, just like Decartes' room. A solid sphere has three dimensions usually measured by the distance from the center and two angles (longitude and latitude).

QUESTION:
Why there is only time dilatation and no time shrinkage? For me I think there should be time dilatation regarding objects traveling away from each other and shrinkage regarding those closer to each other. As what makes one gets older and the other still young for both of them are moving with same speed relative to each other.

ANSWER:
Thinking how you think something should be does not make it true! You should read my answer about the twin paradox. How fast a clock runs and how fast it appears to actually runs are two different things; see earlier answer.

QUESTION:
While we use the combination of rear and front brakes to stop a motorcycle, I mean we can chose between the the front and rear without any effort, why do cars primarily use the front brakes to stop? Why does the brake pedal engage only the front brake? The rear brake is only seem to be used when the car is parked

ANSWER:
All modern cars have four-wheel braking. So where did you get the idea that the brake pedal engages only the front-wheel brakes? Parking brakes engage only rear wheel brakes. Your confusion may be that the braking causes the front-wheel tires to wear more than the rear-wheel tires; this is due to the car slightly "rocking forward" when stopping and also because in a front engine car more of the weight is likely to be supported by the front tires.

QUESTION:
This is a kinematics question about the motion of wheels; specifically, about how friction between a wheel and a surface causes forward motion of the entire wheel. There's something unsatisfactory to me about how this forward motion is typically explained. Consider the rear wheel of a bicycle; it is driven by torque applied to the wheel (via chain drive connected to pedals, etc.). In the classical treatment of this scenario, it is claimed that the friction between the wheel and the road surface, which is a forward-pointing force, causes forward motion of the wheel. But this frictional force is tangential! So wouldn't this tend to be a rotational force instead of one of displacement? It would seem to me that somehow the tangential rightward force of friction at the point of contact needs to be transformed into a rightward force applied at the *center of mass* (i.e., at the axle) of the wheel in order to explain an induced forward/rightward motion, but no source that I have found has attempted to explain this gap.

ANSWER:
The figure shows all forces on the rear wheel of a bicycle:

C, the force exerted by the chain on the sprocket (radius r),
W, the weight of the wheel (radius R),
N, the vertical force exerted by the ground on the wheel,
f, the frictional force exerted by the ground on the wheel, and
F, the force exerted by the rest of the bike on the wheel.

Note that I have resolved F into its horizontal, H, and vertical, V, components. For any body which cannot be approximated as a point, Newton's second law (N2) has two parts, translational and rotational:

The sum of all forces on a body is equal to the product of the mass (m) and the acceleration (a) of the center of mass of the body;
The sum of all the torques on the body about any axis is equal to the product of the moment of inertia (I) of and the angular acceleration (α) about that axis.

You seem to think that a force which exerts a torque about the axis you have chosen (I will choose the axle for the bike wheel) only can cause angular acceleration; in fact, every force on the object contributes to the translational acceleration. Suppose now that you are standing on the pedal but also applying the front brake such that the bike remains at rest; both translational and angular acceleration are zero. So the translational N2 yields two equations, N-W-V=0 and C+f-H=0; the rotational N2, choosing the axle as the axis, yields Cr-fR=0. (F, W, and N exert no torque about the axle.) If you now release the brake, H will get much smaller and the wheel will start moving forward and rotating.

If you are interested in the entire bike, not just the rear wheel, the force C has no contribution to the motion because it is an internal force; the chain exerts a force C on the rear sprocket but a force -C on the front sprocket netting zero net force.

FOLLOWUP QUESTION:
You say, "in fact, every force on the object contributes to the translational acceleration" but the force, f, in your answer, is not directed at the center of mass of the wheel. I guess my question is simply, "why is f treated as a force directed at the center of mass and not as a torque on the wheel"? I don't understand where the forward acceleration of the *center of mass* of the wheel is coming from.

ANSWER:
You did not read my answer carefully. The translational N2 is "The sum of all forces on a body is equal to the product of the mass (m) and the acceleration (a) of the center of mass of the body". Note that it does not say …the sum of all forces which are directed through the center of mass… Let me give you a simpler example. Suppose that you are in the middle of empty space and you have a wheel which has a string wrapped around its circumference. You pull on the string so that the tension in that string is the only force on that wheel and it is tangential. Surely you do not think that your pulling will cause the wheel to only spin and not accelerate toward you too. Here is another example, a yoyo. There are two forces on it, its own weight which passes through the center of mass and points down and the tension of the string which you are holding which points up and does not pass through the center of mass. If the string does not affect the translational acceleration, the only force on the yoyo would be its weight so it would fall with acceleration due to gravity, g, which it clearly does not do.

SECOND FOLLOWUP QUESTION:
In classical billiards problems, for example, when a force is applied to a ball, the force has to be decomposed into its normal component directed at the center of mass (call it f_n) and the tangential component (call it f_t). Only f_n will cause translation, right? It's my understanding that f_t will only contribute a torque, but not to translation. So why is the bike case any different? Contact friction between the wheel and the surface is a tangential force, so, according to my understanding, it can not cause translation, because it has no component directed at the center of mass of the wheel...

ANSWER:
Look at the figure*. It is much better to resolve F into its horizontal and vertical components rather than normal and tangential components. It is wrong to insist that a force must be directed toward the center of mass for that force to contribute to tranalational motion; my examples above should have convinced you of that. Now, a billiard ball is confined to move on the table, so there will be no translational motion in the vertical direction. So the ball is in equilibrium in the vertical direction, so N-V-W=0. But in the horizontal direction there will be an acceleration, ma=H-f. Only f and F will exert torques and it will be a little tricky to calculate the torque due to F but just geometry. I have drawn the line of force to be below the center of mass; if it is through the center of mass, it will exert no torque and only f will cause angular acceleration.

Here is the take-away for you: just use N2 as I have given it to you, always look at all forces on the object, and do not continue insisting that a force which exerts a torque does not affect translation.

*I have drawn the forces on the ball, which are

the ball's weight W,
the normal force N the table exerts vertically on the ball,
the frictional force f the table exerts horizontally on the ball, and
the force F exerted on the ball.

QUESTION:
A hammer hitting an anvil creates energy (sound) which moves in all directions at about 700 mph in atmosphere. Sound energy is also created by a large fire. In space, vaccuum, that same energy must also be present if a hammer hits an anvil in space, same as a star (a large fire ball) should also create sound energy, along with all the other energies it creates, so if sound energy in space, a hammer hitting an anvil, does not have atmosphere to slow it down, or to make noise, how would one measure that energy, its speed and pressure. Could this be what is called "Dark Energy".

ANSWER:
Sound is a wave that exists in a solid, liquid, or gas. If you are in a vacuum, there is no sound. The energy which the sound carried away in air is instead retained as sound in the anvil (and hammer). But this sound eventually damps down and where that energy goes is an increase in the temperature of the anvil (and hammer). This energy eventually radiates away, not as sound but as electromagnetic waves (mainly infrared) until thermal equilibrium is achieved. It certainly has nothing to do with dark energy.

QUESTION:
So my question is a bit out of reality question as its not possible to do this in real life. But if you were able to turn a cannon ball into a musket ball and fire it from a flintlock, having the ball turn back into a cannonball apon exiting the gun, would the cannonball retain its velocity after changing or would it lose all energy and drop to the ground?

ANSWER:
Essentially what you are asking is if an object with a certain mass m and speed v suddenly loses or gains mass, what happens? The mass either disappears without trace or appears without a source. Suppose your musket ball has a mass m and speed v and your cannon ball has a mass M. Since there are no external forces on the ball, linear momentum must be conserved, that is mv=MV where V is the speed of the cannon ball. So V=mv/M, much smaller than v. However, the energy is not conserved: E₁=½mv² and E₂=½MV²=½mv²(m/M)=(m/M)E₁; a large amount of energy is lost.

QUESTION:
How many pounds per inch does a lacrosse ball exert when it hits a surface? For info: Ball is traveling 90mph. A lacrosse ball weighs 8 ounces. The ball is 5.25 inches in circumference. As a sidebar, does it matter if the surface the ball hits is stiff like a wall or springy like a bounce-back? If so, could you expand on the difference in pressures against the two different surfaces?

ANSWER:
If it is pressure you want, you should ask for pounds per square inch. But I do not think that is what you really want; it is more straightforward to estimate the average net force the ball exerts on whatever it hits. Then you could think about pressure, how that force is spread over the area which the two surfaces have touching; pretty hard to do that, though. If something with mass m with a velocity v₁collides with a much more massive object at rest and rebounds with velocity v₂, the average force F can be estimated as F≈m(v₂-v₁)/t where t is the time the collision lasts. ("Much more massive" means the struck object does not recoil significantly.) You seem to want to get answers in imperial units (lb, ft, s); without going into details, m=0.5 lb/(32 ft/s²)=0.016 lb·s²/ft=0.016 slug and v₁=90 mph=132 ft/s. Suppose that v₂=0, called a perfectly inelastic collision; then F=-132x0.016/t=(-2.1 lb·s)/t. So, the smaller the time, the larger the force. (The fact that the force is negative means that this is the force the struck object exerts on the ball because I have chosen the incoming velocity to be positive. The force the ball exerts on the object is positive and equal in magnitude.) That addresses your second question: the ball will certainly stop in a much shorter time when hitting a hard surface than a soft one. Of course that should not be too surprising to you because you know that if you fall onto a mattress it hurts much less than if you fall on a concrete floor. So, if t=1 s, F=2.2 lb whereas if t=0.01 s, F=220 lb. Now, if the ball hits a hard surface it does not penetrate very far and therefore the force is spread over a small area and pressure is large. If the ball hits a soft surface, it penetrates deeper and therefore the force is spread over a larger area and pressure is smaller.

QUESTION:
Since this isn't technically a homework question and was a challenge put out to the class to see if anyone can do it, I hope you will consider it. I'm attempting to do some fun physics maths as a challenge from our professor. It may be a trick question though since she's done that in the past. The problem assumes that c is only 30000 kmph. The problem was to determine the time to reach 29999 kmph from 25000 kmph with a total of 6.48MN of force in a vehicle that weighs 168000kg (168t) in the vacuum of space, too far away from any celestial body to have gravity noticeably affect it. So just to clarify, there is no air resistance or gravity or time dilation. Relative mass increases when reaching said 30000kmph, and the goal is to find the time it takes to accelerate to 29999kmph from 25000kmph.

ANSWER:
I don't see the point of this odd choice of c; it makes the problem neither easier nor harder, just unphysical! You will still have to do some work! I am going to point you in the direction of solving it yourself. First, go to an earlier answer; you will see that I have solved your problem but starting at rest. If you start at some initial velocity v₀, the result is that Ft=p-p₀. Here, p is the relativistic linear momentum, p=mv/√[1-(v/c)²] where m is the rest mass, 1.68x10⁵ kg in your case; similarly, p₀=mv₀/√[1-(v₀/c)²]. So now you know everything except t, so just solve for it; this is just algebra/arithmetic. I would advise you to convert everything to SI units (kg, m, s) before doing your calculation. Then t will work out to be seconds.

I do not understand what you mean by "…there is no…time dilation…" since time dilation is simply not of any interest here but would come into play if the whole thing were seen by an observer in a different frame. Also, I almost never apply the idea of relativistic mass because I view the linear momentum as being the quantity redefined in relativity, not mass. Read my discussion of this in one of the links in the earlier answer.

QUESTION:
Atoms are mostly empty space. How can they form solid objects?

ANSWER:
First of all, atoms are not mostly empty space. See an earlier answer. Although almost all the atom's mass is in a volume much smaller than the volume of the whole atom, the electrons fill the rest of the space in a "cloud". Bohr's model of the atom, tiny electrons in tiny orbits, is wrong. If you need a simpler explanation without reference to the "electron cloud" think of all the atoms connected to their nearest neighbors by tiny springs. Each atom connects to its neighbors by some interaction which can be approximated as a spring. The atoms close enough to interact with each other will stick together and thus form a solid object.

QUESTION:
2 balloons, one filled with 1 cubic meter of air, and the other with 1 cubic meter of Helium, are lowered to a depth of 50 feet under water and simultaneously released. Will they reach the surface at the same time?

ANSWER:
With the information you gave me, I will have to put stipulations on the problem. The baloons are rigid so they do not get compressed under the water, they have identical shapes, their masses (without being filled) are the same, and both are filled to atmospheric pressure. There are three forces on each balloon: its own weight -mg, the buoyant force of the water B, and the drag force opposite the velocity v which has the form -Cv² where C is some constant which depends only on the shape of the balloon. So the net force on each balloon is -mg+B-Cv²=ma where I have put this equal to the mass times the acceleration, Newton's second law. When you release each balloon, each will accelerate up and, as v increases, eventually a=0 and it will have a constant speed v_t, called the terminal velocity, thereafter. It is easy to show that v_t=√[(B-mg)/C] The only difference between the two is m which is smaller for the helium which therefore has the larger terminal velocity. The helium balloon reaches the surface first.

QUESTION:
does a bouncing ball possess simple harmonic motion?

ANSWER:
A bouncing ball is not an example of simple harmonic motion (SHM). By definition, the ball's motion must be describable by simple sinesoidal functions of time t, i.e. like y(t)=Asin(ωt)+Bcos(ωt) where A, B, and ω are constants and y is a variable describing the motion, for example the height above the ground in your case. If the ball were perfectly elastic, the motion would be harmonic, but not SHM, because y(t) would be a train of identical downward-opening parabolas. If it were a real ball, it would not even be harmonic because each subsequent bounce would be a little smaller that the previous bounce.

QUESTION:
What exactly is the 4th dimension? How do we know it's real? How are space and time related?

ANSWER:
I have recently answered this question in some detail.

QUESTION:
As I understand it, electricity moves at the speed of light. Conductivity is where I'm getting stuck on. Are we able to measure speed from it? I tried searching "siemens/meter to kph" with no results. My questions here are these: If silver has a conductivity of 63x10^6 siemens/meter, and copper has a conductivity has a conductivity of 59x10^6 siemens/meter, does that mean energy in silver is travelling faster than copper, or something else? But, silver can't go, say 101% the speed of light. So, there's obviously something else I'm not understanding. I guess the point I'm getting at is this: What does conductivity mean, and can you convert siemens/meter into a speed calculating how many particles move through 1 meter of wire in x amount of time, thus making copper's speed x time/meter, while silver is y time/meter? I'm sorry if this is a bit confusing, or not even your field. But, I figured electricity is, in some part, in the field of physics.

ANSWER:
I am going to give you a qualitative overview since you seem to not have any understanding of what goes on in a conducting wire. If you want a more detailed discussion of the simple model of electric currents, you can find it in any introductory physics text book. A conductor has electrons which are moving around at random in the material, not really bound to any of the atoms; these are called conduction electrons and they can be thought of as a gas of electrons. But there is no flow of current because the electrons move randomly so there are just as many going in one direction as there are going in the opposite direction. When this wire is connected to a battery an electric field is established inside the wire which points from the positive terminal to the negative terminal. When you say "electricity moves at the speed of light", what that means is that the establishment of the field moves with speed c; the electrons do not move at that speed. So all electrons see the field turn on almost immediately. All electrons, having negative charge, begin accelerating in the direction opposite the field. If the only force seen by the electrons was due to the field, they would accelerate until they reached the positive terminal and left the wire. But, even though they are not bound to atoms, they certainly see the atoms and when they hit one they are momentarily stopped or scattered. So each electron is constantly being accelerated, then stopped, then accelerated and the net result is that, on average, all the electrons participating in the current move with a very small velocity, on the order of one millimeter per minute; this is called the drift velocity. All the electrons are continually gaining and then losing kinetic energy and that lost energy shows up in the heating up of the wire. What determines the conductivity is the number of conduction electrons per unit volume of the material as well as its crystaline structure and how individual atoms scatter the electrons.

QUESTION:
The classic escape velocity formula takes in consideration an uniform acceleration of gravity, g. What would be a mathematical model for escape velocity where the force of gravity varies as the body distances from the planet?

ANSWER:
"The classic escape velocity formula" that I know does not assume a uniform gravitational field, it assumes the correct field. Let's see where it comes from. The potential energy for a particle of mass m a distance r from the center of a large spherical mass M is, choosing zero potential at r=∞ is V(r)=-mMG/r where G is the universal gravitational constant. If m has a speed v at r=R, where R is the radius of the earth, the total energy is ½mv²-mMG/R=E. Now, suppose we want v to be big enough that m will go all the way to r=∞ before it finally comes to rest; then E must be zero. Therefore v_e(R)=√(2MG/R); but, MG/R=gR, so v_e(R)=√(2gR). That is the escape velocity at the surface of the planet (ignoring any other forces, notably air drag) where g is the acceleration due to gravity. Now, you want it everywhere else. That's easy, just replace R by r, v_e(r)=√(2MG/r). You could use g=MGr if g now means the acceleration due to gravity at an altitude of r-R. (Incidentally, this does not work anywhere inside the planet.)

QUESTION:
I have a bit of a debate with colleagues and looking for a professionals take. I'm a plasterer and when mixing up the plaster introducing too much air to the mix makes it less workable. Some people I work with think mixing counter clockwise introduces less air to the process than clockwise, I think it would make no difference.

ANSWER:
Well, I just so happen to have a plaster/paint stirring tool which is powered by a drill. Examine it carefully and you will see that clockwise and counterclockwise are not the same in their effect; if the direction is clockwise (as viewed from above), the blades push down on the mixture and if the direction is counterclockwise, the blades push up. I do not know for sure which, if either, of these would introduce more air. My best guess would be that for the clockwise rotation there would be a whirlpool into the surface, whereas for the counterclockwise rotation there would be more of a hump on the surface; I would think the whirlpool would pull in more air. I must also note that not all stirring tools are necessarily of the same design as mine.

QUESTION:
Why does this toy move in a straight line? Shouldn't the toy rotate due to gyroscopic precession? https://youtu.be/hs4iv7IHvGg

ANSWER:
Well, it does not move in a straight line. One thing I noticed is that the toy starts moving immediately when released; this indicates to me that the surface it is on is not level. Just because it is a gyroscope does not mean it will precess. There must be an external torque acting on it; imagine an axis running between the two legs about which you would calculate torque. In the figure that I have clipped from the video you can see the motor and battery and the cds which are rotating; the toy is leaning such that I would certainly expect the center of gravity to be beyond the being above the axis and, were the discs not spinning the toy would certainly fall. If you could put the center of gravity directly above the axis, it would not precess. You can see several instances in the video where the toy is moving in a curved path, and in one case the path is a pretty tight circle; these are due to precession because of the torque due to the weight.

QUESTION:
Would you be marginally taller when on top of a tall building/mountain or at the bottom of the ocean. Does the pressure/gravity change and if so which one makes you taller?

ANSWER:
If you are in the the vicinity of the earth there are two forces which are different between your head and feet, tidal force and pressure force due to the fluid you are in. The tidal force is due to the fact that the gravitational field at your feet is slightly larger than at your head, both pointing down; therefore the net force on you tends to stretch you taller. We can estimate the tidal force because the gravitational field falls off like 1/r²: F_feet/F_head=(r+h)²/r²=[1+(h/r)]²≈1+(h/r)² where r is the distance to your feet from the center of the earth and h is your height; I have used the binomial expansion because h/r<<1. So, F_feet-F_head≈F_head(h/r)². Clearly, either force is going to be approximately equal to your weight, so the tidal force is about mg(h/r)²; if I take h=2 m, mg=1000 N, and r=6.4x10⁶ m, this is about 10^-10 N (2.2x10^-11 lb).

The pressure force is down on your head and slightly larger and up on your feet; so the pressure force tends to compress you shorter. The net force on you is simply the buoyant force which equals the weight of the displaced fluid. If I take your volume to be about 0.02 m³, the buoyant force force is about 1000 N in water and 1 N in air. So, as you can see, the stretching due to the tidal force is negligible to forces due to fluid pressure. So, you will be shorter than your "real" height, but more so in water than air. Therefore you are taller up high in the air than down low in the water.

QUESTION:
I know that at sea level, atmospheric pressure is 14.7 pounds per square inch. I know that the higher in elevation you go, the thinner the air gets and a corresponding decrease in the amount of oxygen such that trying to survive above 16-18k feet is not very easy. My question is this: If you where to drain all of the oceans so that the existing atmosphere before draining was now occupying the void left by the water, would you be able to survive at what was sea level? My thought is that the atmosphere would become so diluted with the oceans gone that you would actually have to travel way below what was sea level to able to survive the atmospheric pressure change and the oxygen dilution. Wondering about this has always bugged me lol.

ANSWER:
The volume of all the oceans is about 1.4x10¹⁸ m³ and their average depth is about 3700 m (about 12,000 ft). Now, dealing with the volume of the atmosphere is tricky because the density of the atmosphere gets smaller with altitude so you have to be careful how you describe volume. The mass of the whole atmosphere is pretty well-known, though, to be about 5.15x10¹⁸ kg; so you can calculate the volume if the whole atmosphere were at sea level pressure where the density is 1.225 kg/m³, 5.15x10¹⁸/1.225=4.2x10¹⁸ m³. So, if the atmosphere were uniform, about 1/3 of it would flow into the emptied oceans. But, it is not uniform so less than 1/3 would come; there would be some base pressure 3700 m below the sea level (since there is no sea now, when I say sea level I mean what it was) which I would estimate to be about the same as the pressure at sea level was because 3700 m is small compared to the radius of the earth, 6.4x10⁶ m (0.06% smaller). Since the oceans occupy about 70% of earth's surface, sea level pressure would be about what the current pressure is at about 12,000 ft, the height of a modestly high mountain and certainly habitable. The highest habitable place on earth is about 16,000 ft, so lots of places (like Denver) habitable now would not be. And certainly nobody would be climbing Mt. Everest in this new world!

QUESTION:
What are the signs that show scientists that some particles have a quark structure and others do not?

ANSWER:
Quarks are something which were hypothesized after most of the elementary particles and their properties were known. There are three kinds of particles, hadrons, leptons, and field quanta. Leptons are few, electrons, muons, and neutrinos. Field quanta are also few, photons, gluons, Z bosons, W bosons, and the Higgs boson. Hadrons are many, the proton and neutron being the best known, but what has been referred to as a "zoo" of other hadrons. To try to systemize and explain this array of particles, first group theory and then, building on that, introducing hypothetical particles called quarks was extremely successful. There is no way I could answer "what are the signs" because the "signs" are all the hadrons and their properties.

QUESTION:
What is the difference between a force and weight

ANSWER:
A force is a push or a pull. Weight is the name for a specific kind of force, one which is caused by gravity. For example, your weight is the force which the earth's gravity pulls you down; the gravity on the surface of the moon is smaller and therefore your weight is smaller there. All weights are forces but not all forces are weights.

ADDED COMMENT:
You should be aware that a few textbooks define weight as being what a scale measures. So if you are in an upward accelerating elevator you have a larger weight. I find this to be total nonsense.

QUESTION:
If time slows down near massive objects, how fast is time in the space between Galaxies ?

ANSWER:
Suppose that your clock ticks off a time t if you are in a region of space where there is essentially zero gravitational field. Now imagine bringing your clock a distance R from a spherical, nonrotating object of mass M. The same time interval will now be given by t'=t√[1-(MG/(Rc)] where G=6.67x10^-11 m³kg^-1s^-2 is the universal gravitational constant and c=3x10⁸ m/s is the speed of light. For example, let the location be on the surface of the earth, M=6x10²⁴ kg, R=6.4x10⁶ m; then, t'=t√[1-7x10^-10]≈t[1-3.5x10^-10]. So, for example, the clock in space would click off 1 second while the clock on the earth would tick off 1-3.5x10^-10 seconds. To see significant gravitational time dilation requires a larger M, for example a black hole; for a black hole with a Schwartzschild radius R_S, the time dilation equation becomes t'=t√[1-R_S/R] so time stops when R=R_S. If R=2R_S, t'=0.7t.

FOLLOWUP QUESTION:
Previous answer did not address this question : If time slows down near massive objects, HOW FAST IS TIME IN THE SPACE BETWEEN GALAXIES? Could you do the math at a distance of 10,000 light years from any mass, please.

ANSWER:
There is no answer to that question because time depends on the observer, it is relative. Any observer in any frame of reference and in any gravitational field will say that it takes any clock in his frame 1 s to advance 1 s. Let's take the case of the black hole example above. The observer in empty space sees his clock advance 1 s but observes the clock of the girl near the black hole to advance in 0.7 s in that time. The girl near the black hole sees her clock advance 1 s but observes the clock in empty space to advance 1.4 s in that time.

QUESTION:
In the theory (?) of quantum entanglement, maybe you could clear up some basic things for me: a) in order for two particles to be entangled - no matter how far apart in space they are - must those same identical two particles have been physically 'partnered' up at some point in the past? b) If a particle in a spin up/spin down position is OBSERVED, it chooses (?) to become spin up or spin down. WHY does the act of observation force it to make that choice? Or is that even the right question? I understand that this idea of observation causes change goes to the heart of quantum physics, but I'm still trying to get my head around the WHY.

ANSWER:
The answer to your first question is yes, the particles become entangled by interacting with each other. So, for example, if you had two electrons, each with a wave function which is half up spin, half down, unless they have been put into those states by a mutual interaction, they are not entangled. For the second question, the particle does not "choose" anything. Rather, the measurement puts the particle into the state which you observe. The result of a measurement is to observe a single state, not an admixture. So if you have an electron whose wave function is half up, half down, your measurement will either give one or the other, not both; if you observed a large number of electrons, all with the half and half wave functions, you would observe spin up for half your measurements and spin down for the other half.

QUESTION:
The longer the garden hose the less the pressure at the end - Is this a true statement, if so, how much less? It's not a homework problem, it's a heated discussion with spouse, we're 76

ANSWER:
There is a pressure drop for a fluid flowing through a pipe. The main reason is that there is frictional loss due to viscosity of the water and the rubbing of the water on the walls of the hose. The loss depends on the size and length of the hose, the density of water, the flow rate, the viscosity, a constant characterizing the friction for the material, and the change in height if the hose is not horizontal. The physics is complicated, but there is a handy on-line calculator where you can get at least a qualitative estimate of how big an effect it is. I did a calculation for water in a 1 inch diameter, 100 foot rubber hose, and for a flow rate of 3 gallons per minute; I assumed that the hose is horizontal and straight. The results are shown in the figure. The calculated pressure drop is 0.38 psi which you can compare with a typical in-city water pressure of about 40 psi. So the drop is only on the order of 0.1%. If the water flow were much faster, say 20 gallons per minute, the drop would be about 10 psi, a 25% drop.

QUESTION:
I have a question, if the pulling force of mass or acceleration or electromagnetism can cause time dilation... would a pushing force of the repelling force of electromagnetism or the expansion rate of the universe cause reverse time dilation?

ANSWER:
Only speed (magnitude of velocity) matters for time dilation. It is irrelevant how that speed was acquired, attractive or repulsive force.

QUESTION:
What is the meaning behind multiplication in physics? Is multiplication in physics purely mathematical or there is a physical explanation to it? How do we explain the product for example, s=v.t? Is there any meaning behind this? For example, I can say that "Distance is defined as the product of velocity 'times' time"? But what does this even mean?

ANSWER:
Suppose you are in 6th grade. Multiplication is explained as simplified multiple addition, the product of 5 and 3 is 5 plus 5 plus 5. Then we learn all our multiplication tables to not have to figure out all the simple products we might need. This is arithmetic and, indeed, we are taught that it often means something, like in the example above, if we have three baskets, each containing 5 apples, we have 15 apples. And then it starts touching on physics. The area of a rectangle is the height times the width; or, like your example (but not exactly) the distance traveled is the product of the speed and time. But the second example is sort of ambiguous if you think about it. What does "distance traveled" mean? It might mean the distance between the starting and ending points; but if you get there on a winding path, that is not the really the distance you traveled. The problem is that before you get to physics, there is only one kind of number, called a scalar quantity, which you can specify using only a number. Examples of scalars are time, speed, length, area, etc. But, in the physical world, some quantities require more than one number to adequately describe them. The simplest are vectors which require a specification of both magnitude and direction. Examples are force (e.g. 10 lb straight up), velocity (e.g. 25 mph due north), displacement (e.g. 5 ft straight down). Vector quantities are denoted as bold-face, for example F=10 lb straight up. Now multiplication takes on new and different meanings, and the ways we multiply all have a meaning. The easiest to grasp is how to multiply a scalar times a vector: as in arithmetic, multiplication is just repeated addition, so 3F=F+F+F. But, what is the multiplication of two vectors? There are two ways we could imagine multiplying vectors, namely the product is also a vector or the product is a scalar. The scalar product or dot product is defined as A·B=ABcosθ_AB where θ_AB is the angle between the vectors A and B and A and B are the magnitudes of the vectors. An example of a scalar product is the work done by a force F which acts over a displacement d, W=F·d· The scalar product is commutative, i.e. A·B=B·A. The vector product or cross product is defined as A×B=uABsinθ_AB where u is a dimensionless vector of magnitude 1 which is perpendicular to the plane defined by A and B. You can do additional research on your own if you want to understand whether u is "up" or "down" relative to the plane, but vector products are not commutative, A·B=-B·A. An example of a vector product is torque τ caused by a force F a displacement r from an axis, τ=r×F.

QUESTION:
Something that confuses me is that scientists say it takes approx. 8min for light to travel from the sun to earth. So if the sun were to explode we wouldn't know till 8min after. However Einstein gathered that the faster an object travels the more time slows down so as you approach the speed of light time stops. But isn't this just relativity? If you are moving that fast everything seems like it's not moving cause your moving so fast. If time were to actually stop how could it take 8min for us to realize the sun exploded wouldn't we realize it instantly? So why can't you move faster than the speed of light? Wouldn't that just mean things relative to you would seem to be stopped for longer, meaning time doesn't stop when you reach the speed of light?

ANSWER:
See the faq page for an explanation why you can't move faster than the speed of light. Suppose that someone was moving with speed 99% of the speed of light from the sun to the earth, a distance of about 8 light minutes. Because of length contraction the distance would, for her, be shortened 8x√(1-0.99²)=1.13 light minutes and the time for her to get to earth would be 1.1/0.99=1.14 minutes; so she would observe the sun's demise to hit earth in a time of 1.13 minutes, and she would arrive 0.01 minutes later. But, just because she observed the time to be 1.13 minutes does not mean someone on earth does; the earth-bound do not see the distance to the sun to be shorter but see it as 8 light minutes.

QUESTION:
Suppose you have two persons watching universe expanding, one of them is on earth, the other is moving fast towards the end of universe. Both of them are watching it all the time. Does this mean, that the "end" of universe exists twice and each is in a different "position"?

ANSWER:
You miss the whole point of special relativity, that the time and position of some event do not have absolute values. That the traveler will observe the end of the universe to be in a different location and at an earlier time than you do does not imply that the universe ends twice at two different locations; rather, it implies that time and position are different for him than for you.

QUESTION:
I was telling my kids that time is space and explaining the block universe and they asked me, if time is space, then how many minutes are in a mile? It sounds stupid, like it does not have an answer, but the more I think about it, the more it seems like if space is time, it should have a specific answer, and if not, why not?

ANSWER:
I will first give the simple answer without much detail since you are dealing with kids. But your kids must be fairly sophisticated to be thinking about space-time at all, so I will then give a little more background on how space-time (four dimensions) arises. When special relativity is mathematically represented as suggesting a four-dimensional space, the fourth dimension is not represented by time (t) but by x₀=ct where c is the speed of light. So the fourth dimension has units of length just like the original three, x₁=x, x₂=y, x₃=z. So, if x₀=1 mi=t·186,000 mi/s, then t=1/186,000 s=5.38x10^-6 s=9x10^-8 minutes, approximately one nanominute.

Before Albert Einstein developed special relativity, it was generally assumed that time and length are universal and independent. One second for me is the same for anyone else in the universe; similarly, one meter is the same regardless of the position or motion of the meter stick I am measuring. If someone is moving with a speed v along my x axis and I measure the length of his meter stick, I find it is shorter; similarly, if I measure the rate his clock runs, I find that it is slower than mine. We are talking about meter sticks and clocks which, if located in my reference frame, are identical to mine. Mathematically this is expressed in what we call a Lorenz transformation,

x'₀=γ(x₀-βx₁)

x'₁=γ(x₁-βx₀)

where the primed coordinates are in the moving frame as measured by the stationary frame, β=v/c, and γ=1/√(1-β²). So, two of the coordinates in our 4-space get mixed up together if the other frame is moving. Does anything analogous happen in everyday 3-space? The answer is yes; if you take a coordinate system with three axes, (x,y,z) and rotate it through an angle θ about the z-axis, the new x'- and y'-axes both depend on what θ is and they depend on both x and y are:

x'=xcosθ+ysinθ

y'=-xsinθ+ycosθ.

Hence the Lorenz transformation may be interpreted as a rotation in the x-t plane. This is the impetus of mathematically working in a 4-dimensional space (space-time).

QUESTION:
I teach high school physics, and I recently performed a lab to investigate Lenz's law. Given the current state of things, this was done in my own home, with students on video chat timing my experiment with their phones. My experiment involved dropping a cylinder of neodymium magnets (about 3 cm long and 1 cm in diameter) down a 1.5 m long copper pipe about 2 cm in diameter. I marked out different lengths on the outside of the cylinder, and used a steel nail to hold the magnet in place at these various "starting lines." So I could directly drop the magnet 153 cm from the top, and 130, 110, 90, 70 and 50 cm using the nail. For each distance, we did three trials. For each of those trials, seven students recorded through the Google Meet. I expected a bit of a hectic disaster, but the precision of the results was amazing. My idea was to use the graph of distance vs. time to discuss what was happening (they haven't learned about Lenzs law yet) in terms of forces. I talked about different types of graph shapes for different situations and how they relate to what is happening with forces: uniform acceleration, uniform velocity and free-fall with air resistance (terminal velocity). My fingers were crossed that our data would approach linearity like the latter, and it did! A valuable learning experience for all. The one hitch is that the z-intercept of our linear trendline is positive, not negative. When an object goes from rest to terminal velocity, I had shown them that the z-intercept of the linear portion of the graph is negative, because the speed only increases to this section of the graph. With our results, I am forced to conclude that the magnet slows down before achieving linearity, because the average slope of the graph is steeper prior to the domain of our results.

ANSWER:
The questioner said in his initial message that the graph of the data would be included but it was not. I have not been able to get him to reply to any messages, but I spent some time working this all out, so I thought I would go ahead and post it. In doing my calculations I approximated some of the variables with reasonable guesses. I had three neodymium approximately 1 cm magnets which when stacked were about 1 cm; the mass of three was 10 grams so three cm would be about m=30 grams=0.03 kg. I took the acceleration to be about g=10 m/s². I made a wild guess at the terminal velocity by watching videos on the internet and chose v=20 cm/s=0.2 m/s. I also note that many videos seem to indicate that terminal velocity is achieved very quickly. The resistive force is given by F=-bv (not proportional to v² as most air drag problems are) where b is a constant to be determined. I choose the coordinate z to increase in the positive vertical direction and the initial position to be at z=0 and the initial velocity to be v=0. This is a classic problem and I will just state the results which result from solving the Newton's second law equation, -mg-bv=m(dv/dt):

v=(mg/b)[e^-bt/m-1]=0.2(e^-50t-1)

z=(mg/b)[(m/b)(e^-bt/m-1)-t]=0.2[0.02(e^-50t-1)-t]

Note that, for large bt/m, v≈-mg/b=-0.2 which is the terminal velocity. This can be solved for b, b=1.5 N/(m/s).

The plot above for v shows that it takes only about 0.1 s to approximately reach terminal velocity. The plot for z shows z(t) in black and z(t) if the magnet moved with the terminal velocity the whole time; the linear portion of the curve is shifted up by 4 mm, possibly responsible for the "positive z-intercept" observed by the questioner. Of course these plots are not what is being plotted by the questioner because each new datum starts at rest; but every datum plotted has the same behavior as the one I have shown, so all the individual runs are shifted by the same 4 mm. The shift is so small compared with the total fall distances, the non linear time is so small compared with the total fall times that the experiment should be able to extract a reasonably good measurement of the constant b. Unfortunately, I do not have the times of the various data points, so I cannot be more specific; the time of fall from the top if the terminal velocity is 20 cm/s would be 7.5 s.

QUESTION:
Is following the line of steepest topographic descent (as stream would do) an example of conservation of energy?

ANSWER:
Let's take a stream as the specific example to discuss the question. The reason the water flows downhill is that there is a force acting on it, the downhill component of the force of its own weight. Generally a stream of water will tend to follow the path where it finds the greatest force impelling it down, that is the steepest terrain. Now, if that were the only force on the water, it would accelerate and the water would be going faster at the bottom. But, in order to do this, the stream would have to get narrower as you went down because water is basically incompressible and if you have, say, 100 gallons per minute flowing at the top of the hill you need the same flow rate at the bottom where it is flowing faster. (Think of a hose nozzle where the water flows much faster out the nozzle than in the hose.) But this is not what happens because there are drag forces which impede the flow. What you generally find is that, if the stream is about the same depth and width as it moves down the hill, the speed is pretty constant. Therefore the kinetic energy at the bottom is the pretty much the same as at the top but the potential energy has decreased; mechanical energy has decreased, not been conserved. However, if you consider the whole system of the stream, the stream bed, the banks, etc., the energy is conserved because the lost potential energy of the of the water will show up as heat in the environment and the water. However, this would be true regardless of whether or not the water flowed down the steepest path. So, I would not use the choice of steepest path to be an example of energy conservation.

QUESTION:
I tried posting this question on a different website and didn't get much of a response. For some reason there doesn't seem to be a lot of information available about this subject, or maybe I just can't find it. Anyway, I am hoping you can help shed some light on the subject. Please forgive the formatting - I've posted a couple of different questions, but if you need a single, concise question to answer, the main one I have is this: What's going on here?

I have a bottle of water that I put in a freezer for a period of time, until the water becomes super-cooled and is still liquid. Now we know that when we shake or disturb the bottle, some of it crystallizes. But it doesn't turn into solid ice. Instead it turns into slush - a mixture of tiny ice crystals and liquid water. Here are my questions:
What determines what parts of the water will become ice, and which will stay liquid?
What is the temperature of the slush mixture?
Is the water part slightly warmer than the ice part?
or is it all pretty much the same exact temperature?
If I poured out the liquid water into a different bottle, and left the slush / ice in the original bottle, would there be any chemical differences between the two?
Is the explanation that the liquid water has impurities such as minerals, and the frozen water is pure H20?
If that is the case, then if we performed this experiment with pure water, then it should turn directly into solid ice, and there'd be no slush, right?
I have read about Fractional Freezing which seems relevant. But this doesn't seem to fully describe what is happening. I am hoping for more of a general explanation rather than a list of individual answers.

ANSWER:
I recommend that you google supercooled water videos and watch a few. It seems pretty clear to me that your problem with slush is that your water is not pure enough. Possibly not cold enough either so that generated heat warms the water just above zero before it freezes. This is a very touchy sort of experiment, one of the videos has the teacher admitting it took him a number of tries to get a good enough take to post. By the way, I thought the answer on Reddit was pretty good.

QUESTION:
Hi, I have a bee in my bonnet about a real world home improvement matter concerning wall tiles and the surfaces they are stuck to. There is much ado about the supposed weight of tiles per square metre that the sub surface can support and arguements are made for using concrete backer boards which can take greater weights than plasterboard (or drywall if you prefer). So plasterboard can take 30kg/m2 and backer boards 50kg/m2 or more. The base of wall tiling always finishes at a horizontal surface, such as a floor etc. So given there are no gaps between tiles and that the wall is truly vertical, what is the relevance of the supporting weight figures for the subsurface board? I can't see that there would be any force acting that would cause any board to fail assuming the tiles end on a horizontal surface that can take the weight. I follow that there will be compressive force down through the tiles and thus through the backing board by virtue of the adhesive to some degree. But surely this compressive force can't affect the backing board as the weight is carried down through the tiles to the horizontal surface that they connect with.

ANSWER:
Well, this isn't really physics, but having had a recent experience (a backsplash behind our range), maybe I can make a few comments. If the wall is sheetrock and sealed or painted, it is best; this is because the surface is just paper and if it is necessary to provide vertical force, it could be too weak. But, as you state, if the tiles extend all the way to the floor (or other support like a cabinet as in my backsplash), there should be no reason to apply the concrete boards. On the other hand, I would not put tiles on a bathroom sheetrock wall because if moisture gets behind the tiles you would have a mess. The same thing goes for bare wood. I once had laid large terra cotta tiles on my kitchen floor on top of an old pine floor; it turns out I had a slow leak in the ice maker which I did not discover until the tiles started coming up from the saturated spongy wood floor. I had to rip up half the floor and leave it to dry for several weeks before reinstalling (too late for a subfloor because it would have raised the floor too far). When I tiled our laundry room I did use the backing board and it is still in pristine condition after 40 years.

QUESTION:
This is really not a question about astrophysics but something simple I am missing. I know that as two massive objects orbit each other they lose energy by emitting gravitational waves and that eventually the orbit decays and they will collide. However as the Earth and Moon rotate around each other and the system loses energy by tidal forces the Moon moves AWAY from the Earth. Why the difference?

ANSWER:
It is understandable that you would think of this because it would appear that the moon is gaining energy rather than losing energy. In fact, it doesn't just appear to gain energy, it is gaining energy. The reason is rather subtle. The moon causes a bulge in the oceans which is responsible for tides. The bulge is actually two bulges, one toward and one away from the moon as shown in the figure (greatly exaggerated); this is because of the tidal force. Because there is friction between the oceans and the ocean floors, the rotation of the earth drags the bulge forward, so it is slightly ahead of the moon as shown in the figure (again greatly exaggerated). Now the bulge exerts a force on the moon which causes it to accelerate a tiny bit; that's where it gets the added energy to increase its orbital radius. Similarly, the moon pulls on the bulge which causes the earth to slow down. If this were the whole story, the energy would be conserved, the earth losing energy and the moon gaining the same amount. But, as noted above, there is friction between the earth and the oceans which takes energy away from the system, giving a net loss of energy but the moon ends up with more than it started with.

QUESTION:
If subject A is traveling through space at a high rate of speed and subject B is traveling at a much slower rate of speed would you expect to see a difference in the rate at which either subject can process information. Example: Would it be easier for subject A to process information than subject B or vice versa?

ANSWER:
This is too vague. What does "process information" mean? What do you mean by "easier". Now, whatever the answers to these questions are, if each subject is presented with the same information stream in his frame of reference and has the same equipment to process it, they will be equally easy to process. But if you mean that A sends an information stream which he processes to B to process (or vice versa), they will not process the information at the same rate. For simplicity's sake, I will choose the "slow" frame B to be at rest; in relativity, only the relative velocity is important. Let's choose a simple concrete example of information stream: the information is a stream of ten pulses separated by 1 second as seen in the reference frame B; B will process them in 10 seconds. Now, how does A process that same information which B processed in 10 seconds? Suppose A is moving away from B; then the time between pulses will be longer than 1 second because he moves some distance away while waiting for the next pulse to catch up with him—the information is processed more slowly. You should be able to see that if you interchanged A and B everything else would be the same so B would process the information more slowly. Suppose A is moving toward B; then the time between pulses will be shorter than 1 second because he moves some distance toward B while waiting for the next pulse to arrive—the information is processed more quickly. You should be able to see that if you interchanged A and B everything else would be the same so B would process the information more quickly. An earlier answer would be of interest to you.

QUESTION:
Matter wave of a particle depends on its momentum,doesn't that mean different observers with different speed will measure different wavelength?

ANSWER:
Yes. This is called the Doppler shift.

QUESTION:
If I am driving in a vehicle in a straight line at a constant speed and activate a drone in the vehicle so the drone is hovering inside the vehicle, open the back of the vehicle and increase my speed so the drone drifts out the back of the vehicle, what then happens to the drone once it is not longer inside the vehicle?

ANSWER:
There will be a period when the drone is leaving the car when there will be lots of turbulence and other currents of air; I am answering neglecting this transition period and also assuming the air outside the car is still. You have adjusted the drone so that, even though it is moving forward with the car at speed v, it hovers in still air. When it suddenly finds itself outside it sees a headwind of v, not still air. This headwind will exert a force which will tend to slow the drone down so that eventually the drone will be hovering at rest relative to the ground.

QUESTION:
Once a spacecraft breaks free from earth's gravity, how much propulsion does it actually need to reach a destination, say Mars? Would the craft have to continually accelerate through the vacuum of space, or once it reaches its maximum velocity, would its propulsion be turned off?

ANSWER:
Technically, you never "break free from earth's gravity". If you acquire a speed greater than the escape velocity, then you will never fall back to earth, but you will slow down continually forever (assuming you have no other objects exerting forces on you). Nevertheless, the force gets very small pretty quickly. If you are 100 earth radii away from earth, the weight (force of earth gravity) is 1/100²=10^-4 times smaller than on earth. And 100 earth radii is not all that far in the whole scheme of things; the distance to the moon is 60. Anyhow, a spacecraft always coasts nearly all the time on a mission somewhere in the solar system. Propulsion is used mainly for getting up to speed and then slowing down to orbit or land on your destination; a much smaller use is to steer, changing direction.

QUESTION:
I have had this question in my mind for over 10y, and I would be very grateful if you could help me to get an answer. The theoretical experiment goes as follows:
1) Bring to outer space 1 round glass chamber, 1 pure iron ball, and a source of heat. 2) Place the iron ball in the center chamber, and heat it until it gets bright red.
3)Go out of the chamber, close it, and generate a total vacuum.
As far as I have been able to go:
Q1: Can we see the bright red iron bar?
A1: Yes, and considering that the ball is in an absolute vacuum the light must be behavior as a particle. *Quantum mechanics dictate that given the duality of light a media is not necessary for light to travel, thus radiation.
Q2: If the light behavior as a particle it must have a mass. Where does this mass come from?
A2. Given that the iron bar is in an absolute vacuum, my logic dictates that the only source of mass for the photons must be the mass of the iron bar itself... Is this correct?
Q3. After an X amount of time when the iron bar has finally cooled down. Will the iron bar be lighter than at the beginning of the experiment? ** Consider that the energy in the iron bar can only be released in the form of light.
A3: I have been stuck in here for several years.....
Thank you very much for your time, please notice I'm not a physicist but a Biology's with a deep interest in physics.

ANSWER:
I do not see why all the stuff about a glass chamber, heat source, etc. is necessary to ask your question which is, simply: if an object is hot and cools soley by radiation, does the object have less mass after cooling?

First, your A2 is wrong. Photons do not have mass even though they do have momentum and energy. Therefore, your conclusion that the object will be lighter because the photons carry away mass is wrong. However, because mass is just a form of energy, we can say that the photons carry away energy (even though they have no mass). But, where did that energy come from? The object had to provide it. But there are just as many atoms after the cooling as before, so the object evidently changed mass into energy. This change in mass is very difficult to observe in the case of a red hot iron object cooling down. Inasmuch as E=mc², the change in mass would be Δm=ΔE/c² where ΔE is the energy carried off by the radiation. Suppose that ΔE is a real big number, say a 10,000 Joules; then Δm=10⁴/(3x10⁸)²=10^-13 kg=0.1 nanograms! This is approximately the mass of a single yeast cell.

QUESTION:
For a space traveler that leaves Earth headed for a distant star @ 0.9c, wouldn't his onboard clock (that's @ rest relative to him) read the time passes normally......i.e. as if he were still on Earth? He would see no time dilation nor length contraction!

ANSWER:
Wrong. the distance to the star is measured from the earth; think of it as a long stick. The stick is moving with speed 0.9c as seen by the traveler, so he sees the distance shorter by a factor √(1-0.9²)=0.44. Since, as you correctly stated, her clock runs normally, it only takes her 4.4 years to get to a star 10 light years away. It would be worth reading my explanation of the twin paradox which is linked to from the faq page.

QUESTION:
Which is the correct term to refer to the speed of light (scalar) or the velocity (vector) of light. They are both used in books & literature. I think its should be the "speed of light", but just asking.

ANSWER:
It depends on the context. One context is "the speed of light is a constant in all frames of reference and independent of the velocity of the source or observer". Another would be "when a ray of light passes close to a massive galaxy, it is bent and so its velocity changes although its speed does not."

QUESTION:
How do I calculate the kinetic energy of an object moving submerged under water? Specifically if water pressure is involved. Like if a cannonball was fired at 110 m/s under 9,000 feet underwater. Or If a submarine is moving 10 m/s at a depth of 800 feet. I know kinetic energy is factored in and pressure at that depth and possibly water drag. I'm just not sure if there is a specific equation for this. Can you please help me with this?

ANSWER:
The kinetic energy of something depends only on its mass m and its speed v, K=½mv². It has nothing to do with its pressure or its drag force. If there are any forces on the object, those forces do work which might change the kinetic energy. Because of the near incompressibility of water, the depth will have almost no effect in how something moves. The effect of the pressure is simply the buoyant force which is a force equal to the weight of the displaced water which is nearly the same 100 ft down as 10,000 ft down. Similarly, the drag depends only on the density, speed, and geometry, not pressure, the drag will be about the same at any depth.

QUESTION:
What's the physics behind "walking ladders" that move down slopes by themselves? I'm thinking maybe it's the same for slinkys that 'walk' down steps. Gravity and the weight of the ladder being moved around the different legs. I tried Googling for an answer but can't find any scientific answers.

ANSWER:
This was a fun problem to figure out. First, let's think about all the forces on the ladder when it is slightly tipped so that two legs are off the ground. There is the weight W, normal forces (not shown) N_front on the front leg and N_rear on the rear leg, and frictional forces (not shown) f_front on the front leg and f_rear on the rear leg. The weight acts at the center of mass of the ladder which is centered relative to the two sides, but is closer to the front than the rear because the front is heavier. That means that the normal force on the front leg is greater than on the rear leg; this is important to remember as we go further. Now, I want to examine the torque which the weight causes. I have resolved W into components down the incline (W_x) and normal to the incline (W_y). W_y causes a torque about the axis I have labelled DROP AXIS causing the currently-off legs to drop to the ground. The inertia causes the ladder to keep going lifting the other legs off the incline; if none of the legs ever slipped (lots of friction), the ladder would rock back and forth without going forward. Now, the other component W_x exerts a torque about the axis I have labelled TWIST AXIS; if no legs slip, this torque has no effect on the motion. However, for a couple of reasons, the rear leg may slip:

Because the normal force is smaller for the rear leg, the maximum static frictional force will be smaller than for the front leg.

The material contacting the ground may be different for the rear legs than for the front, e.g. the rear legs may have a smaller coefficient of static friction and could slip even if the normal forces were the same.

So, for the video, the rear legs must slip and the ladder, with each "step" twists about a normal axis. There are frictional losses which would cause the ladder to lose energy and therefore eventually stop, but since it is going down an incline, this energy is replenished by the work done by W_x as it moves down the incline. It seems to me that it would be pretty tricky to get this set up since everything must be just right for it to work.

ADDED THOUGHT:
A different possibility occurred to me. I have treated the ladder as if it is rigid. However, if it is kind of rickety the lifted legs will tend, if they can, to move forward because of gravity, even if the two down legs do not slip. So when they come back down they will have moved forward a bit.

QUESTION:
My Dad loves physics and always referred to the speed of light as 186,000 miles per second, per second or 186,000 miles per second sq. that is how he always spoke of it. Is that speed of light an excelleration? (even though nothing goes faster than light.)

ANSWER:
The dimensions for speed are length/time, not length/time/time. Therefore, 186,000 mi/s/s is wrong.

QUESTION:
E=m(c)2
What is the reason for twice the speed of light? Einstein tried everything and found it?

ANSWER:
Oh dear, it is not twice c it is c squared. E=m·c·c=mc². And Einstein did not find it by trial and error; how could he, since it was not really appreciated at the time that mass was, in fact, just another kind of energy? It was a natural result of his theory of special relativity.

QUESTION:
According to Enistine space time is like a fabric and all masses round around the sun so why Moon revolve around Earth not sun?

ANSWER:
Not just the sun, but every object with mass, warps spacetime. It is much easier to think about this in terms of Newtonian gravity for which the equivalent statement is that all objects with mass have a gravitational field. The force which a mass M exerts on a mass m a distance r away is F=MmG/r² where G is the universal gravitational constant. You can calculate the ratio of the force the sun exerts on the moon to the force the earth exerts on the moon:

F_sun/F_earth=(M_sun/M_earth)(R_earth/R_sun)=(2x10³⁰/6x10²⁴)(3.8x10⁸/1.5x10¹¹)²=2.1

So the sun exerts a force more than twice the force the earth exerts on the moon. But if you think about it, the moon does revolve around the sun since it moves right along with the earth; but because of the force the earth exerts, it also revolves around the earth.

QUESTION:
according to law of gravitation less mass object attract toward heavy mass object so why we don't attract toward wall because wall have greater mass then a human mass ?

ANSWER:
Actually, the law of gravitation states that two masses attract each other with equal and opposite forces. So the wall does exert a force on you and you exert an equal and opposite force on the wall. However, since gravity is such a weak force, you do not feel it at all. For example, if you and have a mass of 100 kg and the wall has a mass of 10,000 kg, the force you experience, if you are 10 m away, is about 10x10,000x6.67x10^-11/10²=6.67x10^-8 N=1.5x10^-8 lb.

QUESTION:
I'm trying to calculate what effect hitting a 1,500 lb water barrel at 30 mph in a 15,000 vehicle would have upon the truck's momentum? Also, if I increased the truck's weight to 65,000 and drove it at 50 mph, what difference would this make on the momentum too? I'm working on a road safety prototype in my shed and to be honest this kind of math is way beyond me, so any help would be much appreciated.

ANSWER:
I will assume that the barrel and vehicle move off together after the collision; this is called a perfectly inelastic collision. In a collision the total linear momentum, the product of the velocity times the mass, remains constant. Although lb is not a unit of mass, it is a measure of mass. So, before the first situation you state, the momentum before the collision is 15,000x30=450,000 lb·mph and after it is 16,500v where v is the speed after the collision; equating the two and solving for v, I find v=27.3 mph. For the second case, 65,000x50/66,500=v=48.9 mph.

QUESTION:
I have watched Human Universe with Brian Cox. If you haven't seen it, in part one he goes to Russian to meet with the Soyuz spacecraft. He tells his viewers that only knowing two of Newton's equations (F=ma and the law of gravitation F=GmM/r²) he can calculate that the spacecraft only needs to reduce velocity by 128 m/s to safely reenter orbit. I have looked and tried to figure out how the calculations work but can't. Do you have any clue how he would have done the math?

ANSWER:
I will assume that the Soyuz is returning from the International Space Station. First I will give some information needed later:

R=6.4x10⁶ m (radius of the earth)
h=4x10⁵ m (altitude of the space station)
G is the universal gravitational constant (will not need it)
M is the mass of the earth (will not need it)
m is the mass of Soyuz (will not need it)
g=9.8 m/s²=MG/R² (acceleration due to gravity at r=R)
√(MG/R)=√(gR) (this will be useful later and is why I do not need to know G or M)
MmG/r² is, as you note, the gravitational force on m a distance r from the center of the earth.

If orbits are circular, a=v²/r and you can show that v=√(MG/r). I am thinking that we need to find the difference of speeds between orbits with r=R+h and r=R:

v_R-v_R+h=Δv

=√(MG)[√(1/R)-√(1/(R+h))]

=√(MG/R)[1-(1+(h/R))^-1/2]

≈√(MG/R)[½(h/R)]

=½h√(g/R)

=247 m/s

Note that, because h/R=0.0625 is small compared to 1, I have used the binomial expansion (1+x)ⁿ≈1+nx. My answer is about twice what Green got. Of course, in the real world, air drag when entering the atmosphere would significantly reduce the required speed change due to the additional braking it would cause; but you cannot estimate that using only those two equations. So, I am at a loss to understand the difference.

ADDED THOUGHT:
Maybe the Soyuz dropped to a lower orbit before beginning its reentry, h~200 km, after leaving the ISS, but I could find no reference to its altitude in the video.

QUESTION:
i am currently designing a fully adjustable boom arm for a microphone my prototype is fine and it is functional but i am interested on getting more weight suspension from my joints the joints im using are friction based and use clamping force to lock the joints in the desired position what material should i to use as washers to create more friction in my joints

ANSWER:
it is hard for me to be specific since i do not know what the joints are made of what you need to do is find a material with a larger coefficient of static friction with the material currently in the joints i think the very best way would simply apply trial and error try different materials to see how they work i would start with obvious choices like rubber why dont you use punctuation or capitalization it is very annoying reading your question

QUESTION:
In a fire where does the photons come from? Are photons in a superposition of wave and quanta particles?

ANSWER:
Fire is many chemical reactions going on. The reactions are, for the most part, exothermic and most of the energy comes out as heat and light. Photons are particles which have wave properties.

QUESTION:
I am confused in the formula of orbital angular momentum of electron. According to quantum physics the formula of orbital angular momentum is L=l√(l+1)h/2π B.M. while according to Bhor's postulate the formula of angular momentum is L= nh/2π. Both are giving different result. For example for hydrogen putting n=1 in Bohr formula and l=0 in quantum mechanics formula gives h/2π and 0 respectively.

ANSWER:
I believe there is an error in your question, L=√(l(l+1))h/2π. The answer to your question is that the Bohr model is simply incorrect. As luck would have it, it describes the energy levels of the hydrogen atom well, but it is incorrect regarding angular momentum of the levels.

QUESTION:
Why would a heavy object like a bowling ball not float on top of water, but a wooden telephone pole, which is much heavier, would float? I'm sure the shape and the material the object is made from plays a role but I would just like to know the science behind it.

ANSWER:
The science behind this is over 2000 years old. Archimedes was a Greek mathemetician who discovered what we call today Archimedes' Principle. It says that there is an upward force (called the buoyant force) on an object in a fluid which is equal to the weight of the fluid which it displaces. It turns out that, applying this principle, anything with a density smaller than water floats and anything with a density greater than water sinks. Wood is less dense than whatever bowling balls are made of. You might then ask why a steel battleship can float. It is because it is hollow and therefore the total density is much lower than the density of steel; a hollowed out bowling ball would float.

QUESTION:
I read that metals conduct heat well because the electrons of metallic elements have free electrons in its outer shell that move quickly when heated. These quickly moving electrons transfer their kinetic energy to other electrons which vibrate quickly and collide with other electrons and transfer the heat energy and so and so forth. I also read that metals conduct electricity well because the electrons of the outer shell are free to move (as is the definition of electricity - the movement of charged particles). So it would reason to stand that heating a metal should generate electricity or at the least facilitate the production of electricity as both heat conductance and electricity involves the movement of electrons in terms of metals. To my surprise after a google search, I learned that heating a metal does not generate electricity, and furthermore hampers (not facilitate) electric conductance. Please dear physicist help me to understand why hot metals are poor conductors of electrons.

ANSWER:
In a conductor, there are "free electrons" which essentially behave as an electron gas. There is normally no net current because, just as there is no wind in still air, the electrons move in random directions and the net flow is zero. If you apply a voltage across a conductor, these moving electrons, on average, flow from the negative to the positive terminals. Since they are now experiencing a force due to the electric field, they accelerate; but, obviously, they do not really speed up the whole time that they move from one end to the other of the conductor but, on average, move with some constant speed called the drift velocity. The reason is that they are not really free; rather, they accelerate for some short distance and then collide with one of the atoms in the solid which scatters them, then accelerate again, then collide again, etc. Now, all the atoms in the solid are constantly vibrating as if attached to tiny springs, and the hotter the metal gets, the larger the amplitudes of their vibrations becomes. This means that they present bigger targets for the electrons to hit and so collisions happen more often which reduces the drift velocity and therefore the conductivity.

QUESTION:
I was confused about the strict physics definition of a wave. Considering it is a traveling disturbance that carries energy, would wind on a field, an audience created "wave", and dominoes falling be waves? I thought the audience would not be a wave, and I was unsure about the dominoes because there is no wavelength or period.

ANSWER:
The "strict physics definition of a wave" is that it is something which satisfies the wave equation. The solutions of a one-dimensional wave equation are always of the form f(x-vt) where f is any function; for example where x is the position, t is the time, and v is the speed at which the disturbance travels through the medium which supports it. For your examples: dominos falling and people in a stadium sitting and standing are both waves, but wind is not. Wind is an example of the entire medium moving but that would not be described by a wave equation. The stadium wave would not be a wave if the fans all all just ran around together, like a hurricane of people.

QUESTION:
In my understanding of time dilation if one has a clock in constant motion relative to me I will measure the time ticking off on that clock as slower. However from the other clocks view it is just as valid to say that I AM in motion so an observer traveling along with that clock would measure my clock as moving slower. How is that reconciled? Especially if at some time in the future both clocks are brought together at rest with each other to compare clocks? Am I missing the part that acceleration plays here?

ANSWER:
There is no need to reconcile that each observer measures the other's clock to run slower unless you bring the two of them back together into the same reference frame. Acceleration has nothing directly to do with it. So this is the "twin paradox" which we know is not really paradoxical at all. Go to the faq page and find "twin paradox".

QUESTION:
We have been taught that the big bang created all heavenly bodies as we understand them. I'll disagree with that. Were the exo-planets we have discovered thus far created by the same creation event that brought forth us, Mars and Venus or was it something else that lead to the Gliese's and the Kepler's?

ANSWER:
Good grief, nobody claims that the big bang created everything as it is right now. The big bang created a huge amount of energy (from where, nobody knows) and physical laws. From that point the universe evolved over time eventually atoms, stars, galaxies, planets, etc. appeared. To see a timeline of the universe, click here.

QUESTION:
I'm designing a special suction tube for dental practitioners (I'm an orthodontist) and have a basic question I feel I should know. I want to maintain as MUCH air flow through the tip of the suction tube(end of the tube by the patient's mouth) as possible. The lumen of the suction at the dental unit has a cross sectional area of 75mm2. This tube sucks the air from the patient's mouth into the dental unit. If I use a tube that has a much smaller lumen EXCEPT at the patient's mouth where the cross sectional area would be 75mm2, will I lose air flow? Another way of asking this is: am I required to keep the cross sectional area of the ENTIRE tube at 75mm2 in order to maintain the same flow rate at the tip of the suction (patient's mouth) that I have at the dental unit?

ANSWER:
I learned something new: in physics, lumen is a measure of luminous flux. Biolgists, though, use it as a measurement of inner space of a tubular structure; apparently it is just the cross-sectional area of the tube since the questioner specifies the area of the opening. If you were dealing with an ideal fluid, incompressible, no wall drag, no viscosity, you could argue that the flow would be constant, the speed in the narrower part of the tube would be larger, but the volume per unit time flow would be the same. But air is not incompressible and energy loss effects are not negligible. In order for you to maintain the same volume flow rate you would need a more powerful pump which is pulling the air. Think of trying to drink through a pinched straw–you have to suck harder to get the same amount of drink.

QUESTION:
I have a question for you. So from what I've learnt, Einstein's Theory of Relativity says that an object with mass will bend light towards it by way of its gravity and the source and direction of the light will therefore appear differently to an observer. Besides that, Einstein also says that E=mc^2 and thus m=E/C^2 so something like light, with measurable energy, would have a measurable mass. My question is, just like that object with mass pulls light towards it with its gravity, can light also pull that object towards it with its gravity? Similarly to how an object falling to Earth pulls on the Earth itself? Or does light not have gravity in the same sense as objects with actual mass on account that its mass is relativistic and not actual, classical-physics mass?

ANSWER:
For the first part of your question, see an earlier answer. (You could also have found this on my faq page.) The answer to your second question is that the theory of general relativity finds that any energy density warps spacetime, that is causes a gravitational field; a photon has energy and therefore creates gravity; keep in mind how small this is when compared to any macroscopic mass.

QUESTION:
This is not a homework question, I am actually a teacher and saw this question in a textbook and would like to know if this is a valid question to ask a third-grader. I may be wrong but I do not believe that the pound and ounce are units of measurement for mass. I have tried looking it up online and did not find anything useful. Which two units of measurement are used to measure mass?
Gram
Pounds
Ounce
Kilogram

ANSWER:
Kilograms (kg) and grams (g) (1 kg=1000 g) are units for mass. Pounds (lb) and ounces (oz) (1 lb=16 oz) are units for force. This is very confusing because of the ways weight is measured in different countries. In countries where Imperial units are used, weight (the force which the earth pulls down on something) is measured in pounds (which is correct) and we think that this must also be a measure of mass (the amount of stuff there is). In countries where SI units are used weight is measured in kilograms (which is incorrect) and we think that this must also be a measure of force. I will leave it up to you to decide whether third-graders can understand this subtle difference!

QUESTION:
I know that in a solid the particles are still in motion, but I was wandering if their is any point in the state of matter where the particles are completely motionless? (something like before solid)

ANSWER:
The Heisenberg uncertainty principle stipulates that you cannot know to absolute precision both the position x and momentum p (mass times velocity). Stated mathematically, ΔxΔp≤ℏ where ℏ is the rationalized Planck constant (a very tiny number and Δ denotes the uncertainy of the quantity. So if the velocity (momentum) uncertainty is zero (particle perfectly at rest), the uncertainty of the position of the particle is infinite—the particle could be anywhere in the universe.

QUESTION:
how can the calculations for the curvature of space-time under general relativity be correct without the mass-energy associated with dark matter taken into account? I am just a retired attorney trying to educate my self about our physical world.

ANSWER:
Keep in mind that I specify on the site that I do not do astronomy/astrophysics/cosmology, so you may wish to take my answer with a grain of salt. When you refer to the "curvature of space-time" you are actually talking about the gravitational field. And, you are certainly right, dark matter, if it actually exists, would affect the field. I believe that it is actually the other way around: by studying the gravitational field you can infer something about the distribution of dark matter. The most well-known such inference has to do with rotating galaxies and how the angular velocities of the stars varies with distance from the center. If the only gravity in our Milky Way galaxy were from stars and gas which we know are there, the galaxy would not be able to hold together, stars at larger radii would have speeds far too large. The Wikepedia article on dark matter halos would be of interest to you.

QUESTION:
If a toy car hits a wooden block and pushes it along the track, do the wooden block and the car have the same level of energy or does the energy of the car decrease and the energy of the block increase?

ANSWER:
You have described a perfectly inelastic collision, one in which the two colliding bodies stick together after the collision. I am assuming that the block is at rest before the collision. So linear momentum is conserved and energy is not conserved. I will denote the velocity of the car before the collision to be V, the velocity of the car/block after the collision to be U, the mass of the car to be M, and the mass of the block to be m. Conservation of linear momentum gives MV=(M+m)U or U=V[M/(M+m)]. Note that U<V, so the car has lost energy and the block has gained energy.

If you are interested you can calculate the change in energy (ΔE=E_after-E_before) for each:

ΔE_car=½M(U²-V²)=½MV²[ (M²/(M+m)²)-1]

ΔE_block=½MU²=½MV²[M²/(M+m)²]

For example, if M=m, ΔE_car=-(3/4)[½MV²] and ΔE_block=(1/4)[½MV²]. The car lost three fourths of its initial energy and the block gained one fourth of the initial energy. In this case, half of the total energy was lost. In this case, half the speed was also lost.

QUESTION:
The question is about Maximum gradient a vehicle can climb. The maximum friction force that can be transferred to the road cannot be more than μmgcosθ. As far as I know, μ cannot be greater than 1 (irrespective of contact patch size) for a Rubber tyre on concrete road. At 45 degrees, the drag due to gradient (mgsinθ) is equal to the Normal force (mgcosθ). Any more than 45 degrees, and the drag force increases and Normal force decreases, thus making the vehicle's tyres slip due to loss of traction. Now, I see videos of RC cars on youtube climbing gradients well over 54 degrees. Could you explain this? Is the μ value greater than 1?

ANSWER:
Your analysis is fine if the vehicle is a point mass. But, the video you refer to has the failure to climb a steep incline due to the vehicle tipping over backwards rather than slipping. I will assume the truck shown above is at rest because it is easier to visualize and exactly the same as if it were moving up with constant speed. The whole weight mg may be considered to act at the center of mass of the truck (white cross) which is located a distance h above the ground, a distance d₁ behind the front axle, and a distance d₂ in front of the rear axel, as shown. There are three equations, sum of the forces along the ramp equals zero, sum of the forces perpendicular to the ramp equals zero, and sum of the torques about the point where the rear wheel touches the road equals zero:

f₁+f₂-mgsinθ=0

N₁+N₂-mgcosθ=0

(d₁+d₂)N₂+hmgsinθ-d₂mgcosθ=0

Now, we are interested in when the truck will start rotating backward about the rear axle; when it is just about to do that, the normal force N₂=0. So, the third equation tells us that tanθ=d₂/h; therefore the maximum angle before tipping is θ_tip=arctan(d₂/h). For example, if d₂=1.5 m and h=1 m, θ_tip=56.3⁰. What determines tipping is just where the center of mass is; you want it as far forward and as close to the ground as you can.

But, if you lose traction, slip, before you rotate, you do not need to worry about rotating. As you correctly surmised above, the truck will start slipping when θ_slip=arctan(μ) where μ is the coefficient of static. I agree with you that μ=1 is a reasonable estimate for rubber on dry concrete. However, the video you sent is not done on a concrete ramp, rather the surface appeared to be carpet. Since the tire tread can press into the carpet pile, it is not surprising that μ>1 for those videos.

QUESTION:
How does a single speaker unit play an audio clip consisting of sound frequency of different magnitude? It's the same speaker and has only one 'vibrating membrane' to induce the sound in the air to propagate. How does this single membrane generate sound waves of different frequency and different amplitude simultaneously?

ANSWER:
Sound waves are linear, i.e. if several are acting on a point in space, the net action is simply the sum of all the soundwaves. As an example, I have plotted three waves representing the individual sounds, each with different frequencies and different amplitudes, at some point in space as a function of time. The net sound at this point in space is simply the sum of the three, shown by the black curve. Your speaker need only be driven to vibrate like this; this is pretty easy to do, usually with a magnet attached to the speaker cone and inside a coil, the current in which varies like the black curve.

If you did not find what you are looking for, it has probably been archived. For the most recent archived file, click here.