I will use a specific numerical example but will include general equations so that you may apply it to any specific problem.  I will call the coordinates in the spaceship x’, y’ and your coordinates x, y.  The relative motion has the spacecraft moving with speed v=0.8c in your positive x direction where c is the speed of light.  The velocity c’ of the photon as seen in the spacecraft makes an angle of 37⁰ relative to the y’ axis and therefore has components  and .  The appropriate transformation equations to find the components of the velocity c as seen by you are

and

Notice that the speed of the photon as seen by you is the same as seen by the other observer,  as it must under the central postulate of special relativity.  So, the way the photon velocity vectors look to the two observers is:

 

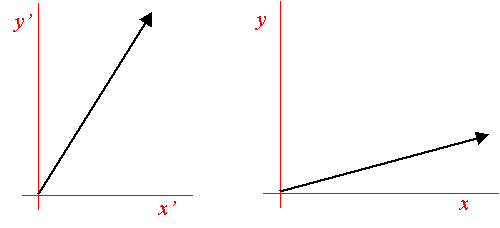
The time it takes to go from the emitter to the screen for the two observers can be found using time dilationmoving clocks run slowly.  So, if the observer in the spacecraft measures the time to be  seconds, you will observe an elapsed time of , a much longer time.